Chapter 1 Simple Linear Regression
Regression is a statistical technique that involves describing the relationship between one or more independent variables and a single dependent variable. For simplicity, assume for now that there is just a single independent variable. To establish some notation, let
- X be an independent variable, also called an explanatory variable, predictor variable, or regressor, which is typically assumed to take on fixed values (that is, X is not a random variable) which can be observed without error, and
- Y be a dependent variable, also called a response variable, which is typically a continuous random variable.
The relationship between the independent variable X and the dependent variable Y is often established by collecting n data pairs denoted by (X1, Y1), (X2, Y2), …, (Xn, Yn), plotting these pairs on a pair of axes, and looking for a pattern that can be translated to a mathematical form. This process establishes an empirical mathematical model for the underlying relationship between the independent variable Y.
1.1 Deterministic Models
Regression analysis establishes a functional relationship between X and Y. The simplest type of relationship between X and Y is a deterministic relationship [latex]Y=f(X)[/latex]. In this rare case, the value of Y can be determined without error once the value of X is known, so Y is not a random variable when the relationship between X and Y is deterministic. The deterministic model is described by [latex]Y=f(X)[/latex]. Deterministic relationships are uncommon in real-world applications because there is typically uncertainty in the dependent variable. If data pairs (X1, Y1), (X2, Y2), …, (Xn, Yn) are collected and the deterministic relationship [latex]Y=f(X)[/latex] establishes the correct functional relationship between X and Y, then all of the data pairs will fall on the graph of the function [latex]Y=f(X)[/latex].
Figure 1.1: A deterministic linear relationship between X and Y.
Long Description for Figure 1.1
The horizontal axis X ranges from 0 to 8 in increments of 1 unit. The vertical axis Y ranges from 0 to 400 in increments of 100 units. The ordered pair X 1, Y 1 is plotted at (6, 30); X 2, Y 2 is plotted at (8, 400); and X 3, Y 3 is plotted at (2, 100). A line with a positive slope begins from the origin and passes through the three plotted points. All data are approximate.
Determining the relationship between the number of sales per week X and the commissions paid per week Y did not require the collection of any data to determine the function [latex]Y=f(X)[/latex]. That linear relationship was implicit in the problem statement. Other cases can arise, such as (a) the relationship is deterministic but requires data to determine its functional form, or (b) the relationship is deterministic, but unlike the relationship in the previous example, it is not linear. The following example illustrates a nonlinear deterministic relationship between the independent variable X and the dependent variable Y.
In most applications, the relationship between the independent variable X and the dependent variable Y is not deterministic because Y is typically a random variable. The next section introduces some of the thinking behind the development of a statistical model that describes the relationship between X and Y.
1.2 Statistical Models
The goal in constructing a statistical model is to write a formula that adequately captures the governing probabilistic relationship between an independent variable X and a dependent variable Y. This formula might be used subsequently for prediction or some other form of statistical inference. In this section, we assume that the dependent variable Y is a continuous random variable that can assume a range of values associated with a particular setting of the independent variable X. The relationship
that was used in the previous section is no longer adequate because X is assumed to be observed without error, and this formula results in a value of Y which is deterministic rather than random. One way of overcoming this problem is to replace the left-hand side of this equation by the expected value of Y, which is a constant, resulting in
To be a little more careful about what is meant by this statistical relationship, the left-hand side is actually a conditional expectation, namely
In words, given that the independent variable X assumes the value x, the transformation [latex]f(X)[/latex] gives the conditional expected value of the dependent variable Y. Notice that this statistical model does not specify the distribution of the random variable Y for a particular value of X; it only tells us the expected value of Y for a particular value of X. This statistical regression model defines a hypothesized relationship between the observed value of X on the right-hand side of the model and the conditional expected value of Y on the left-hand side of the model. The hypothesized relationship might be adequate for modeling or it might need some refining. There is typically no model that perfectly captures the relationship between X and Y. This was recognized by George Box, who wrote:
All models are wrong; some models are useful.
In a statistical model that involves parameters, the estimation of the model parameters will be followed by assessments to determine whether the model holds in an empirical sense. If the model needs refining, the new set of parameters are estimated and new assessments are made to see if the refined model is an improvement over the previous model. Regression modeling is an iterative process.
There is a second way to write a statistical model that is equivalent to the statistical model described in the previous paragraph. The model can be written as
where the error term ϵ (also known as the “noise” or “disturbance” term) is a random variable that accounts for the fact that the independent variable cannot predict the dependent variable with certainty. This term makes the relationship between X and Y a random (or statistical or stochastic) relationship rather than a deterministic relationship. If the probability distribution of the error term is specified, then not only is the expected value of Y conditioned on the value of X determined, but also the entire probability distribution of Y conditioned on the value of X is specified. It is common practice to assume that the expected value of ϵ is zero. The probability distribution of ϵ establishes the nature and magnitude of the scatter of the data values about the regression function. When the population variance of ϵ is small, the values of Y are tightly clustered about the regression function [latex]f(X)[/latex]; when the population variance of ϵ is large, the values of Y stray further from the regression function [latex]f(X)[/latex].
Regression modeling involves determining the functional form of [latex]f(X)[/latex] from a data set of n data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex]. The statistical model for X and Y in a general sense also applies to each of the data points, so
for i = 1, 2, . . . , n. The sign of ϵi indicates whether the observed data pair (Xi, Yi) falls above [latex](\epsilon_i > 0)[/latex] or below [latex](\epsilon_i < 0)[/latex] the conditional expected value of Yi, for i = 1, 2, . . . , n.
The function [latex]f(X)[/latex] is called the regression function, and was first referred to in print as such by Sir Francis Galton (1822–1911), a British anthropologist and meteorologist, in his 1885 paper titled “Regression Toward Mediocrity in Hereditary Stature” published in the Journal of the Anthropological Institute. He established a regression function relating the adult height of an offspring, Y, as a function of an average of the parent’s heights, X, which had been adjusted for gender.
The regression function [latex]Y=f(X)[/latex] can be either linear or nonlinear. The next section focuses on the easier case, a linear regression function. In this case, the model is typically referred to as a simple linear regression model, which is often abbreviated as an SLR model. The model is simple because there is only one independent variable X that is used to predict the dependent variable Y. The model is linear because the regression function [latex]f(X)=\beta_{0}+\beta_{1}X[/latex] is assumed to be linear in the parameters β0 and β1. The more complicated cases of multiple linear regression, which involve more than one independent variable, and nonlinear regression, in which [latex]f(X)[/latex] is not a linear function, will be introduced later.
1.3 Simple Linear Regression Model
A simple linear regression model assumes a linear relationship between an independent variable X and a dependent variable Y. In this section, the more general regression model
is reduced to the simple linear regression model given in the definition below.
Definition 1.1 A simple linear regression model is given by
where
- X is the independent variable, assumed to be a fixed value observed without error,
- Y is the dependent variable, which is a continuous random variable,
- β0 is the population intercept of the regression line, which is an unknown constant,
- β1 is the population slope of the regression line, which is an unknown constant, and
- ϵ is the error term, a continuous random variable with population mean zero and positive, finite population variance σ2 that accounts for the randomness in the relationship between X and Y.
Stating the simple linear regression model in this fashion will not seem natural from probability theory. As a non-regression illustration from probability theory, [latex]W \sim N(\mu, \sigma^{2})[/latex] indicates that W has a normal distribution with population mean μ and population variance σ2. Although much less compact, the probability distribution of W can also be written as [latex]W = \mu + \epsilon[/latex], where [latex]\epsilon \sim N(0, \sigma^{2})[/latex]. This illustration reflects the essence behind writing the simple linear regression model in the form [latex]Y=\beta_{0}+\beta_{1}X + \epsilon[/latex] in Definition 1.1.
The formulation of the simple linear model from Definition 1.1 involves a random variable ϵ on the right-hand side of the model. In some settings, this model might be viewed as a transformation of a random variable, but this is not the correct interpretation of the model in this setting. The simple linear regression model defines a hypothesized relationship between the random variable on the left-hand side of the model and terms on the right-hand side of the model. This probability model is hypothesized to govern the relationship between X and Y. The goal in constructing a simple linear regression model is to determine if it adequately captures the probabilistic relationship between X and Y. Estimation of the model parameters will be followed by assessment to see if the model holds in an empirical sense.
The assumption that the random variable ϵ has population mean zero and population variance σ2 in the most basic simple linear regression model in Definition 1.1 allows for mathematically tractable statistical inference. In models that allow for confidence intervals and hypothesis testing concerning the estimated slope and intercept, the error term is assumed to have a specific distribution, which is typically the normal distribution. The error term models all sources of variation, both known and unknown, other than the variation in Y associated with the particular level of X. Notice that σ2 is constant over all values of X.
The assumption that the independent variable X is not subject to random variability is not always satisfied in practice. The fitting procedure becomes more complicated when X is considered to be a random variable. For this reason, we assume that the observed value of X is either exact or that the variation of X is small enough so that its observed value can be assumed to be exact.
The assumption of a linear relationship between X and Y might also be flawed. In some cases it might not be a perfectly linear relationship, but a linear relationship provides a close enough approximation between X and Y to be useful for associated statistical inference. In other cases, a linear relationship might be appropriate for some range of values of X, known as the scope of the model, but not others. One important step in establishing a simple linear regression model is to specify the values of X for which the simple linear regression model is valid.
The procedure for establishing a simple linear regression model that relates the dependent variable Y to the independent variable X is given below.
- Collect the data pairs. The data pairs are denoted by [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex]. In some settings, it is possible to exert some control over the Xi values. As will be seen later, there are advantages to having the Xi values spread out as much as possible in terms of the precision of the fitted regression model.
- Make a scatterplot of data pairs. A scatterplot is just a plot of the points [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] on a set of axes. The purpose of the scatterplot is to see if the linear relationship between X and Y is appropriate and to visually assess the spread of the data values about the regression function. With modern statistical software, scatterplots are easy to generate.
- Inspect the scatterplot. Although this step is subjective, it is important to visually assess
(a) whether the relationship between X and Y appears to be linear or nonlinear, (b) whether the spread of the data pairs about the regression function is small or large, and (c) whether the variability of the data pairs about the regression function remains constant over the range of X values that have been collected. - State the regression model. In this chapter, the regression model is assumed to be the simple linear regression model [latex]Y=\beta_{0}+\beta_{1}X + \epsilon[/latex]. Nonlinear regression models, such as the quadratic model [latex]Y=\beta_{0}+\beta_{1}X +\beta_{2}X^{2} + \epsilon[/latex], and multiple regression models with more than one independent variable, such as [latex]Y=\beta_{0}+\beta_{1}X_{1} +\beta_{2}X_{2} + \epsilon[/latex], will be considered later.
- Fit the regression model to the data pairs. The method of least squares, which will be described in the next section, is commonly used to estimate the parameters in the regression model. The least squares criterion is to choose the regression model that minimizes the sum of the squares of the vertical differences between data points and the fitted regression model.
- Assess the adequacy of the fitted regression model. Visual assessment techniques for assessing the fitted regression model include superimposing the fitted regression model onto the scatterplot of the data pairs and examining a plot of the residuals. A residual is the signed vertical distance between a data pair and its associated value on the regression function. In addition, there are statistical methods that can be applied to the fitted regression model to see if it adequately describes the relationship between X and Y.
- Perform statistical inference. Once the fitted regression model is deemed an acceptable approximation to the relationship between X and Y, it can be used for statistical inference. One simple example of statistical inference that occurs often in practice is the prediction of a future value of Y for a particular level of X.
The seven steps for establishing a regression model are not necessarily performed in the order given here. Many times the fitted regression model is rejected in Step 6, and it is necessary to return to Step 4 in order to formulate an alternative model. Steps 4 through 6 might need to be repeated several times before arriving at an acceptable model for statistical inference.
The simple linear regression model given in Definition 1.1 implies that all of the [latex](X_{i}, Y_{i})[/latex] pairs also follow the simple linear regression model:
for [latex]i = 1, 2,\ldots, n[/latex], where
- (Xi, Yi) are the data pairs, for [latex]i = 1, 2,\ldots, n[/latex],
- Xi is the value of the independent variable for observation i, which is observed without error, for [latex]i = 1, 2,\ldots, n[/latex],
- Yi is the value of the dependent variable for observation i, which is a continuous random variable, for [latex]i = 1, 2,\ldots, n[/latex],
- β0 is the population intercept of the regression line,
- β1 is the population slope of the regression line, and
- ϵi is the random error term for observation i which satisfies
- [latex]E[\epsilon_{i}]=0[/latex] for [latex]i = 1, 2,\ldots, n[/latex],
- [latex]V[\epsilon_{i}]=\sigma^{2}[/latex] for [latex]i = 1, 2,\ldots, n[/latex],
- the random ϵi values are mutually independent random variables, which implies that their variance–covariance matrix is diagonal.
When the simple linear regression model is stated in this fashion, four properties become apparent. First, Yi is a random variable that can be broken into two components: a deterministic component [latex]\beta_{0}+\beta_{1}X_{i}[/latex], and a random component ϵi, for [latex]i = 1, 2,\ldots, n[/latex]. Second, Yi has population mean
for [latex]i = 1, 2,\ldots, n[/latex] and population variance
for [latex]i = 1, 2,\ldots, n[/latex]. Using slightly different notation, it would be reasonable to write the population mean and variance as the conditional expectations
for [latex]i = 1, 2,\ldots, n[/latex]. The property that the variance does not change with Xi is known as homoscedasticity. Temporarily dropping the subscripts, the line
with β0 and β1 replaced by the associated estimated values [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex], is oftentimes superimposed onto the scatterplot to visualize the fitted regression model. Third, each data pair (Xi, Xi) has a Yi value that misses the regression function by the error term ϵi, for [latex]i = 1, 2,\ldots, n[/latex]. Fourth, the values of the observed dependent variables Y1, Y2, …, Yn must be mutually independent random variables because the error terms [latex]\epsilon_{1}, \epsilon_{2},\dots, \epsilon_{n}[/latex] are mutually independent random variables.
1.4 Least Squares Estimators
We now turn to the question of estimating the intercept β0 and the slope β1 by the method of least squares. German mathematician Carl Friedrich Gauss (1777–1855) invented the least squares method and French mathematician Adrien–Marie Legendre (1752–1833) first published the method in 1805. The least squares method determines the values of β0 and β1 that minimize the sum of the squares of the errors, where the error is the vertical distance between the Yi value and the fitted regression line. The term estimator will be used here to refer to a generic formula for [latex]\hat{\beta}_0[/latex] or [latex]\hat{\beta}_1[/latex]; the term estimate will be used to refer to a specific numeric value for [latex]\hat{\beta}_0[/latex] or [latex]\hat{\beta}_1[/latex].
One bit of notation that will make the expressions of the point estimators more compact is
Similarly,
and
This new notation allow us to express [latex]nS_{XY}[/latex], [latex]nS_{XX}[/latex], and [latex]nS_{YY}[/latex] as
and
Using this notation, the least squares estimators for the slope and intercept of the model, denoted by [latex]\hat{\beta}_1[/latex] and [latex]\hat{\beta}_0[/latex], are given in the following theorem. Notice that the term normal equations in the theorem is not related to the normal distribution.
The requirement that there are at least two distinct Xi values in Theorem 1.1 is consistent with intuition. Figure 1.3 shows [latex]n=5[/latex] data pairs in which the independent variable assumes the same value for each pair: [latex]X_{1}=X_{2}=X_{3}=X_{4}=X_{5}=3[/latex]. It is not possible to estimate the slope of the regression line in this particular setting. This is the geometric reason for the requirement that there are at least two distinct Xi values. In addition, the denominator in [latex]\hat{\beta}_1 = S_{XY} / S_{XX}[/latex] is zero when all Xi values are equal, which gives the associated algebraic reason for the requirement. From this point forward, whenever the simple linear regression model is used, it is assumed that the associated data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] have at least two distinct Xi values.
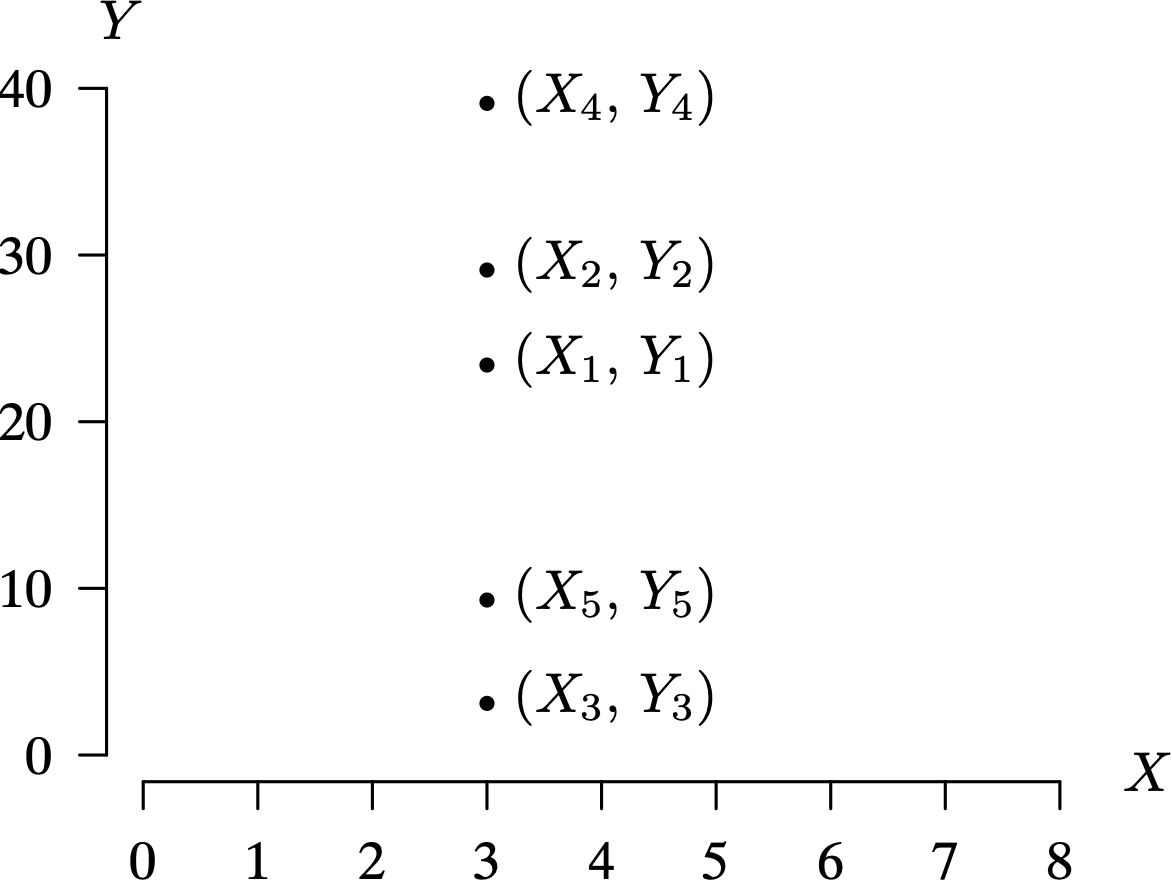
Long Description for Figure 1.3
The horizontal axis X ranges from 0 to 8 in increments of 1 unit. The vertical axis Y ranges from 0 to 40 in increments of 10 units. The ordered pair X 1, Y 1 is plotted at (3, 23); X 2, Y 2 is plotted at (3, 29); X 3, Y 3 is plotted at (3, 2); X 4, Y 4 is plotted at (3, 40); and X 5, Y 5 is plotted at (3, 9). All data are approximate.
Figure 1.4 shows the geometric interpretation associated with the estimated intercept [latex]\hat{\beta}_0[/latex] and estimated slope [latex]\hat{\beta}_1[/latex]. The [latex]n=9[/latex] data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_9, Y_9)[/latex] are plotted as points, along with the associated estimated regression line [latex]Y=\hat{\beta}_{0}+\hat{\beta}_{1}X[/latex]. The y-intercept of the graph [latex]\hat{\beta}_0[/latex] is the height of the estimated regression line at [latex]X = 0[/latex]. The “rise over run” interpretation of the slope is illustrated by the right triangle with legs consisting of dotted lines.
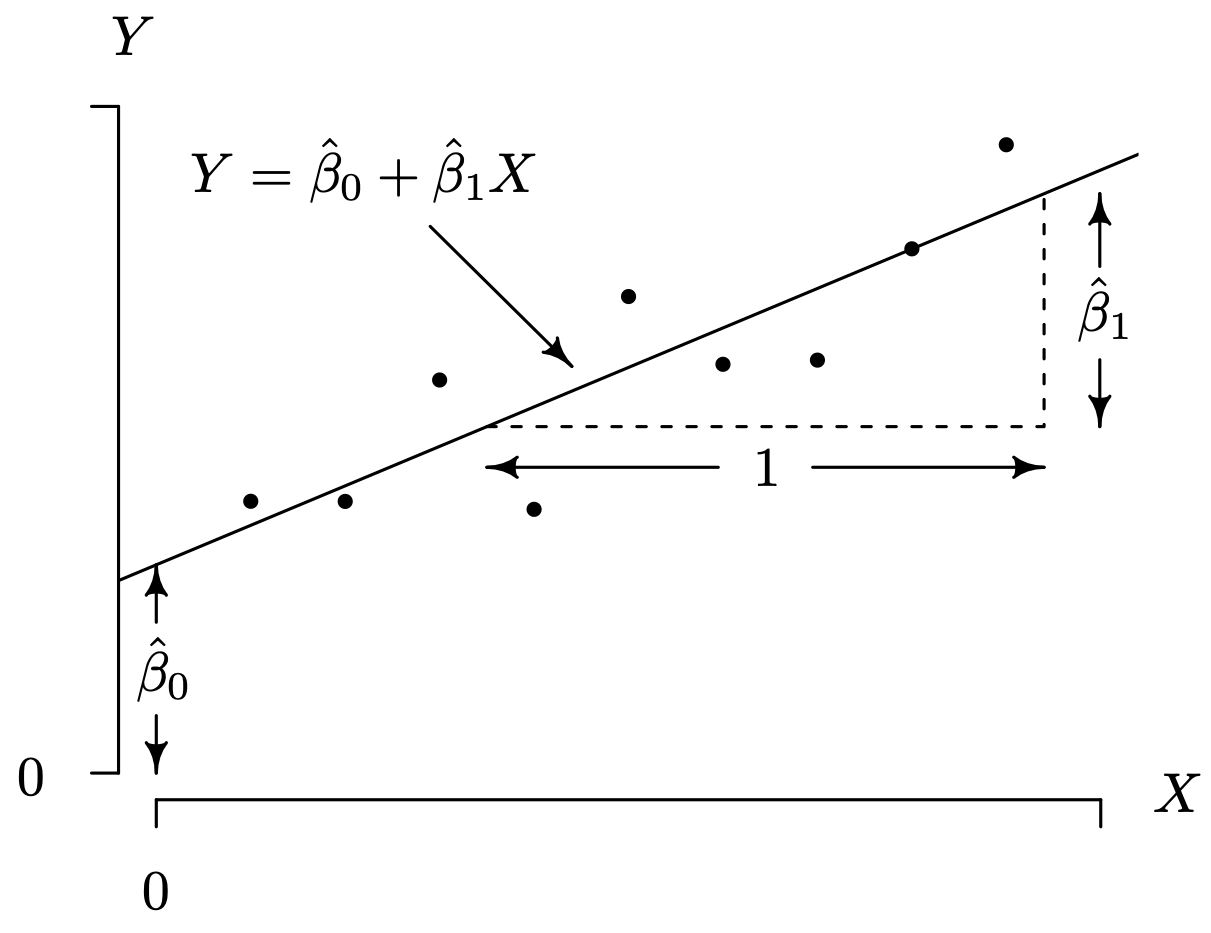
Long Description for Figure 1.4
“9 data points are plotted along the line of regression, which a positive slope and originates from the vertical axis. An equation reading, Y equals beta cap 0 plus beta cap 1 X, is represented by the line of regression. 4 points fall below the line of regression, one point is on the line, and 4 points are above the line of regression. The Y intercept of the regression line, at X value 0 is indicated as beta cap 0. The rise over run of the slope is indicated by a triangle with dotted lines. The height of the dotted triangle, which is parallel to the horizontal axis is labeled 1 and the base that is parallel to vertical axis is labeled beta cap 1.”
The next example illustrates the mechanics associated with calculating the least squares estimates [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. In order to focus on the calculations performed by hand, a small sample size of [latex]n = 3[/latex] data pairs is used. The numbers have been handpicked in order to make the resulting parameter estimates come out to whole numbers. A sample size of [latex]n = 2[/latex] is too simplistic in that two points determine a line, and the estimated regression line will always pass through those two points.
1.5 Properties of Least Squares Estimators
The least squares estimators of β0 and β1 possess several properties which are important for statistical inference. The four properties established in this section are:
- the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] are unbiased estimators of β0 and β1,
- the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] can be written as linear combinations of the dependent variables [latex]Y_{1}, Y_{2}, \dots, Y_{n}[/latex],
- the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] can be written in closed form, and
- the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] have the smallest population variance among all unbiased estimators that can be expressed as linear combinations of the dependent variables.
Proofs of the associated results are included in each of the following subsections.
1.5.1 [latex]\bf \hat{\beta}_0[/latex] and [latex]\bf \hat{\beta}_1[/latex] are Unbiased Estimators of β0 and β1
A key property associated with the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] is that their expected values equal the associated population values β0 and β1. The next result establishes the unbiasedness of the two point estimators.
The fact that the least squares estimators of the slope and intercept of the regression line are unbiased will be supported by a Monte Carlo simulation experiment in the next example. Unlike the typical simple linear regression setting in which data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] are used to estimate the unknown parameters β0 and β1, the simulation will generate data pairs and associated regression lines for known parameters β0 and β1.
1.5.2 [latex]\bf \hat{\beta}_0[/latex] and [latex]\bf \hat{\beta}_1[/latex] are Linear Combinations of [latex]\bf Y_{1}, Y_{2}, \dots , Y_{n}[/latex]
Theorem 1.2, which states that [latex]E [\hat {\beta}_0] = \beta_{0}[/latex] and [latex]E [\hat {\beta}_1] = \beta_{1}[/latex], concerns the accuracy of the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. These estimators are “on target” in the sense that their expected values equal their associated population values. The histograms in Figure 1.11 show that the estimators for β0 and β1 do not systematically deviate above or below their population values.
The precision of the estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] is also of interest. This requires that we also compute their population variances. Before doing so, it is helpful to see that both of these point estimators can be written as linear combinations of the values of the dependent variables [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex]. It is not immediately apparent from the formula for the point estimator for the slope of the regression line [latex]\hat{\beta}_1 = S_{XY} / S_{XX}[/latex], but the estimator can be written as a linear combination of the dependent variables:
because [latex]\bar{Y} \sum^{n}_{i=1} (X_{i} - \bar{X}) = \bar{Y} (n\bar{X} - n\bar{X}) = 0[/latex]. This formula indicates that the point estimator for the slope of the regression line is the linear combination
where
for [latex]i = 1, 2,\ldots, n[/latex].
The coefficients [latex]a_{1}, a_{2}, \dots, a_{n}[/latex] in the linear combination [latex]\hat{\beta}_1 = a_{1}Y_{1} + a_{2}Y_{2} + \cdots + a_{n}Y_{n}[/latex] satisfy three properties. First, [latex]\sum^{n}_{i=1}a_{i}=0[/latex] because
Second, [latex]\sum^{n}_{i=1}a_{i}X_{i}=1[/latex] because
Third, [latex]\sum^{n}_{i=1}a^{2}_{i} = 1 / S_{XX}[/latex] because
These properties can be useful in deriving results associated with the simple linear regression model.
Likewise, the least squares point estimator for the intercept of the regression line is also a linear combination of the Yi values:
This formula indicates that the point estimator for the intercept of the regression line can also be written as a linear combination:
where
for [latex]i = 1, 2,\ldots, n[/latex]. This derivation constitutes a proof of the following result.
These formulas will be illustrated for the small data set consisting of [latex]n = 3[/latex] data pairs.
1.5.3 Variance–Covariance Matrix of [latex]\bf \hat{\beta}_0[/latex] and [latex]\bf\hat{\beta}_1[/latex]
Theorem 1.2 states that [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] are unbiased estimators of β0 and β1 because [latex]E[\hat{\beta}_0] = \beta_0[/latex] and [latex]E[\hat{\beta}_1] = \beta_1[/latex]. This result concerns the accuracy of the least squares estimators, but does not address the precision of the least squares estimators. We now return to the question of assessing the precision of the point estimators. Being able to express the point estimators of the least squares estimators as linear combinations of the dependent variables as summarized in Theorem 1.3 will be very useful as we proceed. In order to assess the precision of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex], it is necessary to compute [latex]V[\hat{\beta}_0][/latex] and [latex]V[\hat{\beta}_1][/latex]. More generally, we will compute the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] in this subsection. Returning to the Monte Carlo simulation in Example 1.4, the magnitudes of the diagonal elements of the variance–covariance matrix reflect the spread of the histograms in Figure 1.11, and the off-diagonal elements of the variance–covariance matrix give the population covariance between [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] which is apparent in the simulation results displayed in Figure 1.12. The general form for the population covariance between [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] will indicate whether the negative sample covariance between [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] that was encountered in the Monte Carlo simulation was due to the particular values of the parameters in the simple linear regression model or whether the negative covariance is generally the case.
We begin with the lower-right-hand element of the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. In the simple linear regression model
for [latex]i = 1, 2,\ldots, n[/latex], the error terms [latex]\varepsilon_1, \varepsilon_2, \dots, \varepsilon_n[/latex] are assumed to be mutually independent random variables. This implies that the dependent variables [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] are also mutually independent random variables. Using the fact that [latex]\hat{\beta}_1[/latex] can be written as a linear combination of the dependent variables from Theorem 1.3, the population variance of [latex]\hat{\beta}_1[/latex] is
because [latex]\sum^{n}_{i=1}a^{2}_{i} = 1 / S_{XX}[/latex] by Theorem 1.3. Although the experimenter typically has no control over σ2, the experimenter may have control over selecting the values of [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] in some applications of simple linear regression. In order to make [latex]V[\hat{\beta}_1][/latex] as small as possible, the experimenter should make [latex]S_{XX}[/latex] as large as possible. Spreading the Xi values as much as possible gives the most stability to the estimated slope of the regression line. Simple linear regression modeling can still be performed when the Xi values are tightly clustered together, but the estimated slope will be less stable, and the scope of the model will be limited. As an extreme example of spreading the Xi values, consider clustering all of the Xi values at a left-most and a right-most extreme possible values for the independent variable. The good news is that this will give you the largest possible [latex]S_{XX}[/latex] and the associated smallest possible [latex]V[\hat{\beta}_1][/latex]. The bad news is that you will not be able to assess linearity in this case because you have observed the dependent variable at only two values of the independent variable. A multitude of functions can model the average of the dependent variables at these two extreme values of the independent variable. So the usual practice is to select the Xi values in an approximately uniform fashion over as wide a range as possible. This gives the experimenter the opportunity to assess linearity and also achieves a large [latex]S_{XX}[/latex], resulting in an associated small [latex]V[\hat{\beta}_1][/latex].
The next step is to calculate the upper-left-hand element of the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. Before calculating the population variance of [latex]\hat{\beta}_0[/latex], it is necessary to establish that [latex]\bar{Y}[/latex] and [latex]\hat{\beta}_1[/latex] are uncorrelated. Since [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] are mutually independent random variables, each with population variance [latex]V[Y_{i}] = \sigma^{2}[/latex], the population covariance between [latex]\bar{Y}[/latex] and [latex]\hat{\beta}_1[/latex] is
because [latex]\sum^{n}_{i=1}a_{i}=0[/latex] by Theorem 1.3. So [latex]\bar{Y}[/latex] and [latex]\hat{\beta}_1[/latex] are uncorrelated.
Based on the fact that the population covariance between [latex]\bar{Y}[/latex] and [latex]\hat{\beta}_1[/latex] is zero, the population variance of [latex]\hat{\beta}_0[/latex] is
The last step is to calculate the off-diagonal elements of the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. Since [latex]\text{Cov}(\bar{Y},\hat\beta_{1}) = 0[/latex], the population covariance between [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] is
All of the elements of the variance–covariance matrix have now been established, which constitutes a proof of the following theorem.
There are two important observations that can be made from Theorem 1.4. First, the elements of the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] are a function of only the Xi values and the typically unknown population error variance σ2; the values of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] do not play a role. Recall from Definition 1.1 that the independent variable observations [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] are assumed to be observed without error. Second, since [latex]S_{XX} > 0[/latex] because at least two of the Xi values are distinct, the population covariance between [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] takes the opposite sign of [latex]\bar{X}[/latex]. This provides an explanation of why [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] appeared to have negative covariance in the results of the 5000 simulated estimates plotted in Figure 1.12.
So far we have found the expected values and the variance–covariance matrix of the least squares estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex]. But there is a lingering doubt as to whether better point estimators for β0 and β1 exist. An example of such a better point estimator would be an unbiased estimator of β0 with a smaller population variance than the least squares estimator of β0. This lingering doubt will be addressed in the next subsection.
1.5.4 Gauss–Markov Theorem
Recall from Theorem 1.3 that the least squares estimators for the slope and intercept of the regression line were expressed as linear combinations of the dependent variables:
and
But are these linear combinations the best possible linear combinations for estimating β1 and β0? The Gauss–Markov theorem is used to show that these estimators have the minimum variance of all possible unbiased estimators which are linear combinations of the dependent variables. These estimators are known as Best Linear Unbiased Estimators, typically abbreviated with the colorful acronym BLUE. The Venn diagram in Figure 1.13 might be helpful in categorizing the various types of estimators. The set L consists of all point estimators for the regression parameters β0 and β1 which can be expressed as linear combinations of the dependent variables [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex]. The set U consists of all point estimators for the regression parameters β0 and β1 which are unbiased estimators of β0 and β1. The shaded intersection of L and U (that is, [latex]L \cap U[/latex]) is all estimators which are both linear combinations of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] and unbiased. An example of an estimator of β1 which is neither in L nor in U is [latex]Y^{2}_{i}[/latex]. The Gauss–Markov theorem states that the least squares estimators have the smallest possible variance among all estimators in [latex]L \cap U[/latex].

The Gauss–Markov theorem indicates that the least squares estimators for β0 and β1 have minimal variance among all linear estimators. It does not indicate whether the least squares estimators for β0 and β1 have minimal variance among all estimators. The Gauss–Markov theorem extends to the case of multiple linear regression in which there are several independent variables. The least squares estimators are also the best linear unbiased estimators in this case.
To review the results that have been introduced so far, the simple linear regression model
defines a linear statistical relationship between an independent variable X, observed without error, and a random dependent variable Y as given in Definition 1.1. The point estimators for β1 and β0 from n data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] using the least squares criterion are
as given in Theorem 1.1. The least squares estimators are unbiased estimators of their associated parameters because
as given in Theorem 1.2. The least squares estimators of β0 and β1 can be expressed as linear combinations of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] as
with coefficients [latex]c_{1}, c_{2}, \dots , c_{n}[/latex] and [latex]a_{1}, a_{2}, \dots , a_{n}[/latex] given in Theorem 1.3. The variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] is
as given in Theorem 1.4. Finally, the Gauss–Markov theorem given in Theorem 1.5 states that the least squares estimators of β0 and β1 have the smallest population variance among all unbiased estimators that can be expressed as a linear combination of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex].
The next section defines fitted values and residuals. Fitted values are the heights of the regression line associated with the observed values of the independent variable [latex]X_{1}, X_{2}, \dots , X_{n}[/latex]. The residuals are the vertical signed distances between the observed values of the dependent variable [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] and the associated fitted values that fall on the regression line. Residuals play an analogous role to the error terms in the simple linear regression model.
1.6 Fitted Values and Residuals
The simple linear regression model
was introduced in the previous section as a linear statistical model for describing the relationship between an independent variable X and a dependent variable Y. Taking the expected value of both sides of this equation yields
because [latex]E[\varepsilon] = 0[/latex] and X is a fixed value assumed to be observed without error, which are two key assumptions in Definition 1.1. When the population intercept β0 and the population slope β1 are replaced by their associated least squares point estimators [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] the resulting estimated regression line is
This estimated regression line is typically plotted on a scatterplot that contains the data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex]. Seeing the data pairs and the least squares regression line on the same plot often makes the visual assessment of linearity easier. For any value X in which the simple linear regression model is valid, [latex]\hat{Y}[/latex] is the point estimator for the value of the dependent variable based on the data pairs and associated estimated regression line. This equation can be rewritten for the particular values of the independent variable collected as
for [latex]i = 1, 2,\ldots, n[/latex]. The value [latex]\hat{Y}_{i}[/latex] is known as the fitted value associated with data pair i, for [latex]null[/latex] [latex]i = 1, 2,\ldots, n[/latex]. When [latex]\hat{Y}_i \ne Y_{i}[/latex], which is almost always the case in applications, the fitted value does not fall on the estimated regression line; when [latex]\hat{Y}_i = Y_{i}[/latex], the fitted value falls on the estimated regression line. The next example illustrates the notion of fitted values for the sales data set.
The spread of the data pair [latex](X_{i}, Y_{i})[/latex] from the fitted regression line [latex]\hat{Y} = \hat{\beta}_0 + \hat{\beta}_{1}X[/latex] is reflected in the vertical signed distance between the data pair [latex](X_{i}, Y_{i})[/latex] and the associated fitted value [latex](X_{i}, \hat{Y}_{i})[/latex], These signed distances are known as the residuals, and are defined by
for [latex]i = 1, 2,\ldots, n[/latex]. Data pairs that fall above the regression line correspond to positive residuals; data pairs that fall below the regression line correspond to negative residuals. The least squares approach used so far in estimating the intercept and slope of the regression line is a matter of finding the values of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] which minimize the sum of the squares of the residuals. In other words, minimize
The fitted values and residuals are formally defined next.
Choosing to use the vertical distance between the observed value of the dependent variable and the regression line in the definition of the residual was based on the fact that the values of the independent variable [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] are assumed to be observed without error in Definition 1.1. The mathematics associated with simple linear regression changes substantially if both X and Y are considered to be random variables.
A subtle but important distinction should be drawn between the model error term ϵi for data pair i and the residual ei for data pair i. The model error terms are defined by
for [latex]i = 1, 2,\ldots, n[/latex], and represent the vertical distances between the observed dependent variable Yi and the true (population) regression line [latex]Y=\beta_{0}+\beta_{1}X[/latex]. The simple linear regression model assumes that [latex]\varepsilon_{1}, \varepsilon_{2},\dots, \varepsilon_{n}[/latex] are mutually independent random variables. In nearly all applications, however, β0 and β1 are unknown. This means that for a particular data set, these model error terms are also unknown. On the other hand, the residuals are defined by
for [latex]i = 1, 2,\ldots, n[/latex], and represent the error for data pair i when compared to the estimated regression line [latex]\hat{Y}=\hat{\beta}_{0}+\hat{\beta}_{1}X[/latex], which is calculated from the n data pairs. Thus, [latex]\hat{\varepsilon}_{i} = e_{i}[/latex], for [latex]i = 1, 2,\ldots, n[/latex]. The [latex]e_{1}, e_{2}, \ldots, e_{n}[/latex] values are not mutually independent random variables because they must sum to zero. (This will be proven subsequently in Theorem 1.6.) For a particular data set, these residuals are known. The residuals are calculated for the sales data next.
A close inspection of the entries in Table 1.2 reveals that there are some curious outcomes that occur, such as
In other words, (a) the sum of the residuals is zero, and (b) the sum of the observed values of the dependent variable equals the sum of the fitted values. These were not just a matter of coincidence. The following theorem confirms that these relationships, along with a few other relationships, are true in general.
These five results from Theorem 1.6 will be illustrated for the sales data in the example that follows.
1.7 Estimating the Variance of the Error Terms
The emphasis so far has been focused on the estimation of the intercept and slope of the regression line. While [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] are the most critical parameters in most applications of a simple linear regression model, there is another parameter, the population variance of the error terms σ2, which should also be estimated from the data pairs.
To establish a foundation for the estimation of σ2, assume for this paragraph only that there is a univariate, rather than a bivariate, sample of values denoted by [latex]X_{1}, X_{2}, \dots , X_{n}[/latex]. These will not be fixed values observed without error as they were in regression modeling. It is assumed that these values constitute a random sample from a population that has finite population mean μ and finite population variance σ2. The goal in this paragraph is to estimate σ2 as a function of the data values. If the population mean μ is known (which is rare in practice), then an unbiased estimator of σ2 is
If the first [latex]n - 1[/latex] deviations between the sample values and the population mean [latex]X_1 - \mu, X_2 - \mu, \ldots, X_{n-1} - \mu[/latex] were known, the final deviation, [latex]X_{n} - \mu[/latex], would be free to take on any value. It is in this sense that the sum of squares
is said to have n “degrees of freedom.” It is common practice in statistics to divide a sum of squares by its degrees of freedom to arrive at a point estimator. In this particular instance, dividing by n makes the point estimator an unbiased estimator of σ2. The problem that arises more often in practice is to estimate σ2 when μ is unknown. An unbiased estimator of σ2 in this case is the sample variance
which is typically denoted by S2 by statisticians. There are three reasons why the term outside of the summation has [latex]n - 1[/latex] in the denominator. The first reason is that this is the appropriate term so that this estimator is an unbiased estimator of σ2. This can be stated as [latex]E[S^2] = \sigma^2[/latex]. The second reason is that one can’t estimate the dispersion of a distribution from a single data value, so the sample variance is undefined when [latex]n = 1[/latex]. The third reason is that the sum of squares has [latex]n - 1[/latex] degrees of freedom. One degree of freedom is lost because the sample mean [latex]\bar{X}[/latex] is used to estimate the population mean μ. If the first [latex]n - 1[/latex] deviations between the sample values and the sample mean [latex]X_{1} - \bar{X}, X_{2} - \bar{X}, \dots, X_{n-1} - \bar{X}[/latex] were known, the final deviation, [latex]X_{n} - \bar{X}[/latex], could be calculated from the other [latex]n - 1[/latex] values because
It is in this sense that the sum of squares
is said to have [latex]n - 1[/latex] degrees of freedom. This ends the discussion of degrees of freedom for a univariate data set.
We now return to the problem of estimating σ2 in simple linear regression. The independent variables [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] are once again assumed to be fixed values observed without error as they have been throughout this chapter. Based on the fact that the error terms [latex]\varepsilon_{1}, \varepsilon_{2},\dots, \varepsilon_{n}[/latex] in the simple linear regression model are assumed to be mutually independent and identically distributed random variables, each with population mean 0 and finite population variance σ2, the population variance of the error terms can be estimated with the unbiased estimator
if β0 and β1 were known. But in practice, the two parameters β0 and β1 are estimated from the data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex], so two degrees of freedom are lost and an appropriate point estimator for the population variance σ2 is given by
It is important that the population variance of the error terms σ2 remain constant over the range of X values in which the simple linear regression model is appropriate. One tool for visually assessing this assumption is a scatterplot of the data pairs with the estimated regression line superimposed.
The point estimator for σ2 when β0 and β1 are estimated from the data pairs involves the sum of squares of the residuals, and this is often abbreviated as SSE, for sum of squares for error:
which is also known as the error sum of squares, residual sum of squares, and sum of squares due to error. When this quantity is divided by its degrees of freedom, it is known as the mean square error, which is abbreviated by MSE:
Some good news is provided by the next result, which states that [latex]MSE = \hat{\sigma}^2[/latex] is an unbiased estimator of σ2.
To summarize, there are three parameters in a simple linear regression model: the population intercept β0, the population slope β1, and the population variance of the error terms σ2. These parameters can be estimated from n data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] by the least squares method. Theorem 1.2 indicates that the least squares point estimator [latex]\hat{\beta}_0[/latex] is an unbiased estimator of β0 and the least squares point estimator [latex]\hat{\beta}_1[/latex] is an unbiased estimator of β1. Theorem 1.7 indicates that the MSE is an unbiased estimator of σ2. All three parameter estimators are on target on average. The next three examples illustrate the estimation of σ2.
The magnitude of the point estimate of σ2 is a reflection of whether the data points are tightly clustered about the estimated regression line (for small values of [latex]\hat{\sigma}^{2}[/latex]) or whether the data points stray significantly from the estimated regression line (for large values of [latex]\hat{\sigma}^{2}[/latex]). In the previous example involving the sales data pairs, there is significant vertical deviation between the data points and the associated fitted values, as seen in Figure 1.15. The next example illustrates the case in which the data pairs are tightly clustered about the regression line.
In the two previous examples, point estimates of the population variance of the error terms σ2 were calculated. In the sales data example, the estimated error term variance [latex]\hat{\sigma}^2 = 14[/latex] indicated that the data pairs strayed a large distance from the estimated regression line, as illustrated in Figure 1.6. In the Forbes data set, the estimated error term variance [latex]\hat{\sigma}^2 = 0.05421[/latex] reflects data pairs that cluster closely to the estimated regression line, as illustrated in Figure 1.18. But these two examples involving individual data sets do not indicate anything about the distribution of [latex]\hat{\sigma}^2[/latex]. The next example addresses this topic by extending the Monte Carlo simulation experiment from Example 1.4.
Before leaving the topic of the estimation of σ2 behind, consider the case of collecting just [latex]n = 2[/latex] data pairs [latex](X_1, Y_1)[/latex] and [latex](X_2, Y_2)[/latex], as illustrated in Figure 1.22. One of the assumptions associated with the observations in a simple linear regression model is that there are at least two distinct values of the independent variable observed. So when [latex]n = 2[/latex], it must be the case that [latex]X_1 \ne X_2[/latex] In this case, the least squares regression line will pass through the points [latex](X_1, Y_1)[/latex] and [latex](X_2, Y_2)[/latex]. This means that the fitted values are identical to the data pairs, and hence, both residuals are zero. So the sum of squares for error is [latex]SSE = e^{2}_{1} + e^{2}_{2} = 0[/latex]. But is an SSE of zero an appropriate estimate for the population variance of the spread of the values about the regression line? Can one conclude that this is really a deterministic relationship and any additional data pairs collected will fall on the fitted regression line? Certainly not, because it is not possible to draw that conclusion based on just two data pairs. A third data pair might fall on the regression line or fall significantly off of the regression line, as was the case with the sales data from Example 1.3. The unbiased estimator of σ2 is undefined because of the [latex]n - 2[/latex] in the denominator of the formula for [latex]\hat{\sigma}^2[/latex], as it should be. Two data pairs are adequate for estimating the population slope and population intercept of the regression line, but they are not adequate for estimating σ2. The mathematics and intuition are consistent in this setting.
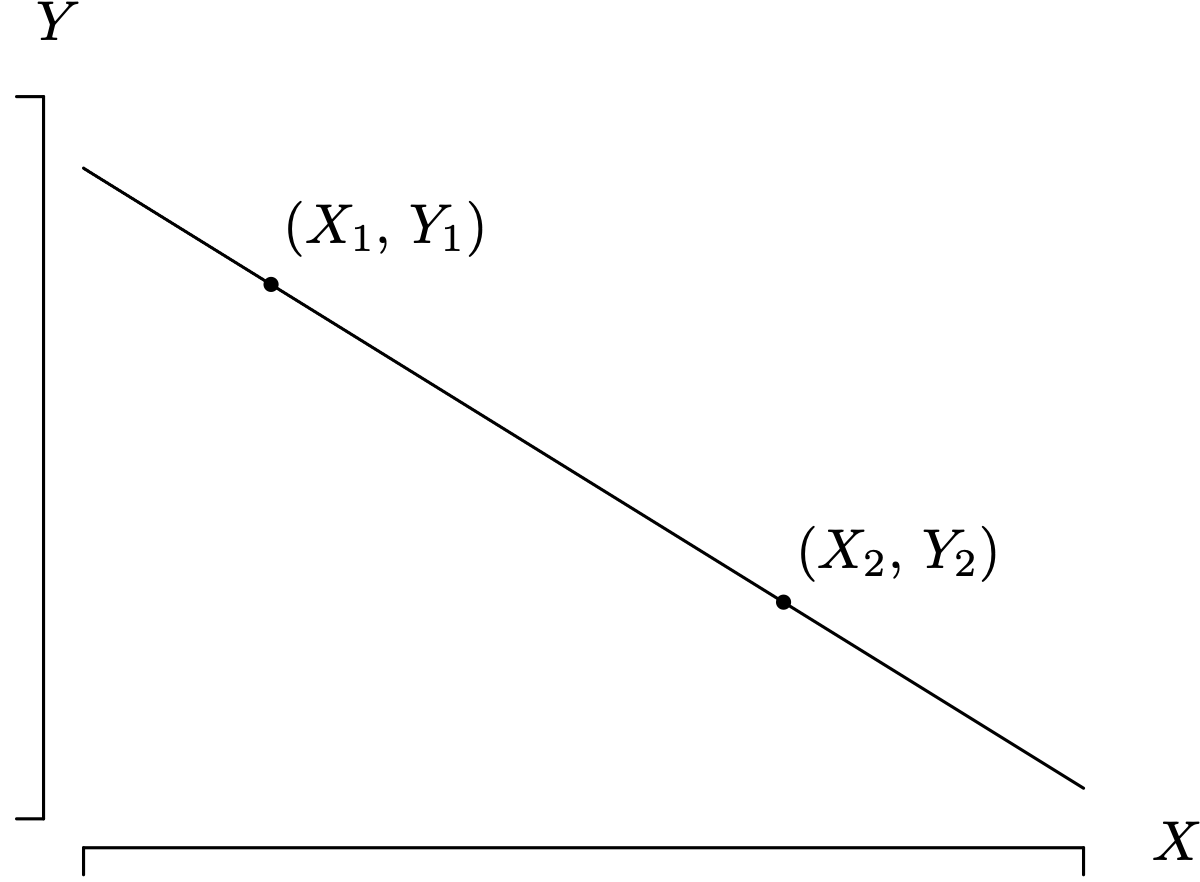
Long Description for Figure 1.22
The horizontal axis is labeled X and the vertical axis is labeled Y. Two data points, X 1, Y 1 and X 2, Y 2, are plotted on a diagonal line with a negative slope. The values of X 1 and X 2 and Y 1 and Y 2 are dissimilar.
1.8 Sums of Squares
Certain sums of squares play a key role in simple linear regression. This section considers three topics related to these sums of squares: (a) partitioning the total sum of squares, (b) defining and interpreting the coefficient of determination and the coefficient of correlation, and (c) displaying the sums of squares in an ANOVA table.
1.8.1 Partitioning the Total Sum of Squares
A topic that is closely related to fitted values and residuals is the partitioning of the total sum of squares. Figure 1.23 provides the geometric framework for the mathematical derivation provided next. There are only three points plotted in Figure 1.23. The first point plotted is [latex](X_i, Y_i)[/latex], which is a generic data pair. The other [latex]n - 1[/latex] data pairs are not plotted in order to keep the figure uncluttered. The estimated regression line associated with the n data pairs, which happens to have a negative slope, is also plotted. The second point plotted is the fitted value [latex](X_i, \hat{Y}_i)[/latex] associated with the ith data pair, which is located directly below data pair i and falls on the estimated regression line. The third point plotted is [latex](\bar{X}, \bar{Y})[/latex], which, by Theorem 1.6, will always fall on the regression line.
Figure 1.23 provides a geometric proof of the relationship
for [latex]i = 1, 2,\ldots, n[/latex]. The relationship can also be established algebraically by recognizing that the right-hand side of this equation can be determined by just adding and subtracting [latex]\hat{Y}_i[/latex] to the left-hand side of the equation. As will be stated and proved subsequently, squaring both sides of this equation and summing results in
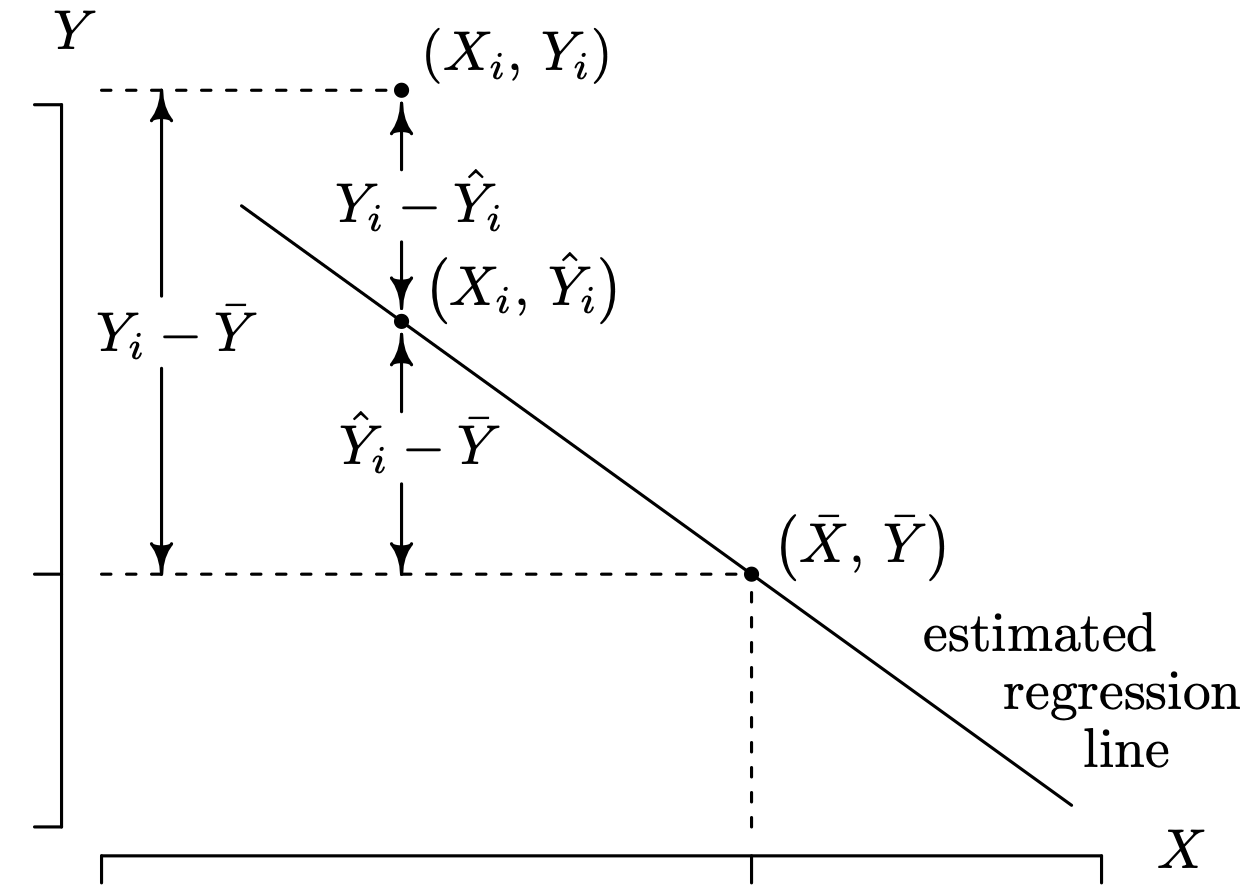
Long Description for Figure 1.23
“Two collinear data pairs (X i, Y i), (X i, Y cap i), and a data pair (X bar, Y bar) are plotted in the quadrant. A diagonal line with a negative slope passing through the points (X i, Y cap i) and (X bar, Y bar) is the regression line. The Y intercept of (X i, Y i) is indicated by a horizontal dotted line. Similarly, the X and Y intercepts of (X bar, Y bar) are indicated by dotted lines. The distance between the data pairs (X i, Y i) and (X bar, Y bar) is indicated as Y i minus Y bar. The distance between the data pairs (X i, Y i) and (X i, Y cap i) is indicated as Y i minus Y cap i. The distance between the data pairs (X i, Y cap i) and (X bar, Y bar) is indicated as Y cap I minus Y bar.”
This equation involves three sums of squares that occur so often in regression analysis that they are given the abbreviations
where SST stands for total sum of squares, SSR stands for sum of squares for regression, and SSE stands for sum of squares for error. (The sum of squares for error has already been encountered in Theorem 1.7.) This equation expresses the total variation of the observed values of the dependent variable [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] about their sample mean [latex]\bar{Y}[/latex] in SST as the sum of two sums of squares. The first term on the right-hand side, SSR, reflects the variation of the fitted values [latex]\hat{Y}_{1}, \hat{Y}_{2}, \dots , \hat{Y}_{n}[/latex] about the sample mean [latex]\bar{Y}[/latex]. The second term on the right-hand side, SSE, reflects the variation of the observed values [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] about their associated fitted values [latex]\hat{Y}_{1}, \hat{Y}_{2}, \dots , \hat{Y}_{n}[/latex]. Since all three terms in this equation are sums of squares, all three terms are nonnegative. Notice that [latex]SST / (n-1)[/latex] is the sample variance of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex].
The equation
partitions SST into two pieces: SSR, which accounts for the total variability in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] that is accounted for by the regression line (that is, the linear relationship between X and Y), and SSE, which accounts for the remaining variability that is not associated with the regression line. This is why SSR measures the total variability in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] “explained” by the relationship between X and Y, whereas SSE measures the total variability in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] left “unexplained” by the relationship between X and Y. It is reasonable to think of SSR as measuring the “signal” associated with the linear relationship and SSE as measuring the “noise” associated with the linear relationship. The result is stated formally and proven next.
1.8.2 Coefficients of Determination and Correlation
There are two measures that are helpful in assessing the degree of the linear relationship between X and Y in a simple linear regression model. The coefficient of determination and the coefficient of correlation are defined next. The thinking behind the way that the coefficient of determination [latex]R^{2} = SSR / SST[/latex] is defined is as follows. The value of SST reflects the variability in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] when the values of the associated independent variables [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] are ignored. The value of SSE reflects the variability in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] when a fitted regression model uses [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] as predictors. Their difference, [latex]SSR = SST - SSE[/latex], reflects the reduction in variability associated with using the regression model. The ratio [latex]SSR / SST[/latex] captures the fraction of that reduction in variability.
The coefficient of determination R2 is the fraction of the variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] about [latex]\bar{Y}[/latex] that is accounted for by the linear relationship between X and Y. Based on the result from Theorem 1.8, [latex]SST = SSR + SSE[/latex], the coefficient of determination must satisfy [latex]0 \leq R^{2} \leq 1[/latex]. Likewise, the coefficient of correlation must satisfy [latex]-1 \leq r \leq 1[/latex], which is true for all population and sample correlations.
Values of R2 that are near 1 indicate that nearly all of the variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] about [latex]\bar{Y}[/latex] can be explained by the linear relationship between X and Y. This in turn implies that X is a useful predictor for Y. On the other hand, values of R2 that are near 0 indicate that very little of the variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] about [latex]\bar{Y}[/latex] can be explained by the linear relationship between X and Y. This in turn implies that X is not a useful predictor for Y. It is in this sense that R2 is a measure of the strength of the linear relationship between X and Y.
There are some important limitations associated with R2 and r. First, it is important to remember that the linear relationship between X and Y might only be appropriate on a limited range of X values. Second, even a relatively large value of R2 might not provide the precision necessary for a particular application. Third, regardless of the value of R2, the scatterplot of the data pairs must always be inspected to see if a simple linear regression model is warranted. Both high and low values of R2 can be associated with a strong nonlinear relationship between X and Y. Fourth, in the case in which the experimenter can control the values of [latex]X_{1}, X_{2}, \dots , X_{n}[/latex], the magnitude of R2 depends on the choices of the independent variables, which clouds its interpretation. Fifth, the usual interpretation of the coefficient of correlation r as an estimator of [latex]\rho = {\text{Cov}(X,Y)} / {\sigma_X \sigma_Y}[/latex] is only appropriate when X and Y are random variables, which is not the case in simple linear regression because X is assumed to be observed without error.
It is a useful thought experiment to consider the scatterplots associated with the values of SST, SSR, and SSE at their extremes. These three extreme cases will be described in the next three paragraphs.
The first of these extreme cases is illustrated for [latex]n = 7[/latex] in Figure 1.24 in which
The only way to achieve a sum of squares for error of zero is to have the data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex] all fall on a line, which is the regression line. Using the result from Theorem 1.8 that [latex]SST = SSR + SSE[/latex], in this case [latex]SST = SSR[/latex], which implies that [latex]R^{2} = 1[/latex]. Therefore, all of the variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] is explained by the linear relationship between X and Y. In addition, [latex]r = -1[/latex] if the slope of the regression line is negative and [latex]r = 1[/latex] if the slope of the regression line is positive.
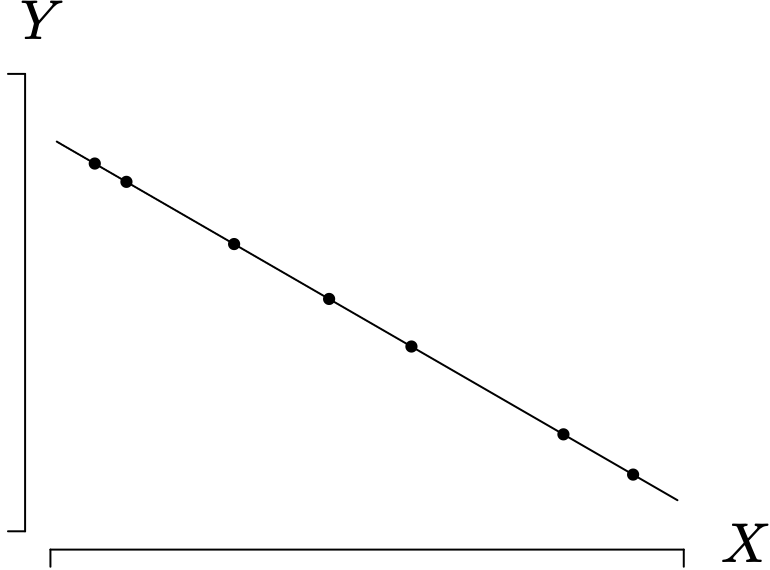
The second of these extreme cases is illustrated for [latex]n = 7[/latex] in Figure 1.25 in which
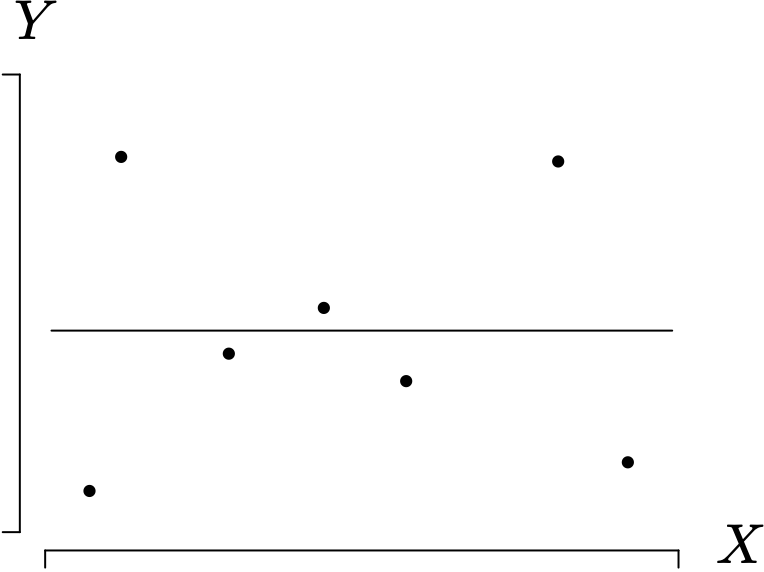
The only way to achieve a sum of squares for regression of zero is to have an estimated regression line with slope zero. Using the result from Theorem 1.8 that [latex]SST = SSR + SSE[/latex], in this case [latex]SST = SSE[/latex], which implies that [latex]R^{2} = 0[/latex]. This means that none of the variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] is explained by the linear relationship between X and Y. In addition, [latex]r = 0[/latex].
The third of these extreme cases is illustrated for [latex]n = 7[/latex] in Figure 1.26 in which
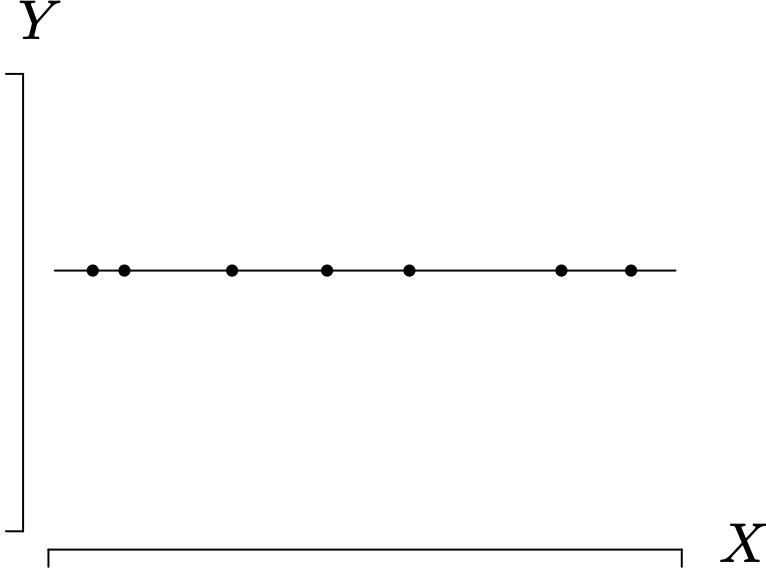
The only way to achieve a total sum of squares of zero is to have an estimated regression line with slope zero and all points lying on the estimated regression line. Using the result from Theorem 1.8 that [latex]SST = SSR + SSE[/latex], in this case [latex]SSR = SSE = 0[/latex], and the coefficient of determination and coefficient of correlation are undefined because the denominator is zero.
Each of the sums of squares has an associated degrees of freedom. The total sum of squares
has [latex]n - 1[/latex] degrees of freedom for either of two reasons: (1) one degree of freedom is lost because [latex]\bar{Y}[/latex] is used to estimate the population mean, and (2) the terms in the summation above are subject to the one constraint—they must sum to zero. The sum of squares for regression
has 1 degree of freedom because each of the [latex]\hat{Y}_{i}[/latex] values is calculated from the same regression line which has two degrees of freedom, but is subject to the additional constraint [latex]\sum^{n}_{i=1} (\hat{Y}_{i} - \bar{Y})=0[/latex] by Theorem 1.6. The sum of squares for error
has [latex]n - 2[/latex] degrees of freedom for the reasons outlined just before Theorem 1.7.
An alternative definition for computing the coefficient of correlation r can save on computation time, as given in the following theorem.
1.8.3 The ANOVA Table
The three sums of squares for the simple linear regression model and their associated degrees of freedom can be summarized in an analysis of variance (ANOVA) table. The four columns in the generic ANOVA table shown in Table 1.5 are (a) the source of variation, (b) the sum of squares, (c) the degrees of freedom, and (d) the mean square. The sums of squares and the degrees of freedom add to the values in the row labeled “Total”. The mean square is the ratio of the sum of squares to the associated degrees of freedom. The regression mean square is [latex]MSR = SSR/1 = SSR[/latex]. The mean square error is [latex]MSE = SSE / (n-2)[/latex]. The mean square entries do not add. Tradition dictates that the mean square associated with SST is not reported in an ANOVA table, but it does have meaning as the sample variance of [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex]. More information on how the ANOVA table can be used for hypothesis testing concerning the population slope β0 by adding a fifth column to the ANOVA table will be given in the next chapter.
|
Source |
SS |
df |
MS |
|---|---|---|---|
|
Regression |
SSR |
1 |
MSR |
|
Error |
SSE |
[latex]n-2[/latex] |
MSE |
|
Total |
SST |
[latex]n-1[/latex] |
The definitions and theorems that are associated with fitted values, residuals, estimating the population variance σ2, partitioning the sums of squares, the coefficient of determination, the coefficient of correlation, and the ANOVA table are briefly reviewed here. The simple linear regression model
from Definition 1.1 establishes a linear statistical relationship between an independent variable X and a dependent random variable Y. The error term ϵ has population mean 0 and finite population variance σ2. The n data pairs collected are denoted by [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)[/latex]. The fitted values [latex]\hat{Y}_{1}, \hat{Y}_{2}, \dots , \hat{Y}_{n}[/latex] are the values on the estimated regression line associated with the independent variables [latex]X_{1}, X_{2}, \dots , X_{n}[/latex]:
for [latex]i = 1, 2,\ldots, n[/latex], as established in Definition 1.2. The associated residuals are defined by
for [latex]i = 1, 2,\ldots, n[/latex], as established in Definition 1.2. An unbiased estimator of the population variance of the error terms is
as given in Theorem 1.7. The total sum of squares SST can be partitioned into the regression sum of squares SSR and the sum of squares for error SSE as
or
as given in Theorem 1.8. Two quantities that measure the linear association between X and Y are the coefficient of determination
which satisfies [latex]0 \leq R^{2} \leq 1[/latex], and the coefficient of correlation
which satisfies [latex]-1 \leq r \leq 1[/latex] as defined in Definition 1.3. The coefficient of determination is the fraction of variation in [latex]Y_{1}, Y_{2}, \dots , Y_{n}[/latex] that is explained by the linear relationship with X. The sums of squares are often presented in an ANOVA table, which includes columns for the source of variation, the sum of squares, the associated degrees of freedom, and the mean squares. An additional column will be added to the ANOVA table in the next chapter, when statistical inference in simple linear regression is introduced.
The point estimators for β0, β1, and σ2 in the simple linear regression model have now all been established and many of their properties have been surveyed. But without additional assumptions, it is not possible to easily obtain interval estimators or perform hypothesis testing concerning these parameters. The next chapter addresses this issue.
1.9 Exercises
-
1.1 Establish a linear deterministic relationship between the independent variable X, the temperature in degrees Fahrenheit, and the dependent variable Y, the associated temperature in degrees Celsius.
-
1.2 Establish a nonlinear deterministic relationship between the independent variable X, the distance between two objects with fixed masses m1 and m2, and the dependent variable Y, the gravitational force acting between the two objects, using Newton’s Law of Universal Gravitation.
-
1.3 For the following interpretations of the independent and dependent variables, predict whether the estimated slope [latex]\hat{\beta}_1[/latex] in a simple linear regression model will be positive or negative.
- The independent variable X is a car’s speed and the dependent variable Y is the car’s stopping distance.
- The independent variable X is a car’s weight and the dependent variable Y is the car’s fuel efficiency measured in miles per gallon.
- The independent variable X is a husband’s height and the dependent variable Y is the wife’s height for a married couple.
- The independent variable X is the average annual unemployment rate and the dependent variable Y is the annual GDP for a particular country.
-
1.4 For the simple linear regression model, show that solving the [latex]2 \times 2[/latex] set of linear normal equations
for [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] gives the expressions for [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] given in Theorem 1.1.
-
1.5 Consider the simple linear regression model
where
- the population intercept is [latex]{\beta}_0 = 1[/latex],
- the population slope is [latex]{\beta}_1 = 1/2[/latex], and
- the error term [latex]\varepsilon[/latex] has a [latex]U(-1,1)[/latex] distribution.
Assume that [latex]n = 10[/latex] data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_{10}, Y_{10})[/latex] are collected. The values of the independent variable X are equally likely to be one of the integers [latex]0, 1, 2,\ldots, 9[/latex], What are the minimum and maximum values that the estimated parameters [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] can assume?
-
1.6 For the values of the independent variables [latex]X_{1}, X_{2}, \dots , X_{n}[/latex], show that
-
1.7 Write R commands to plot contours of the sum of squares for the sales data pairs
in the [latex](\beta_0, \beta_1)[/latex] plane.
-
1.8 The least squares criterion applied to a simple linear regression model minimizes
If instead the least absolute deviation criterion (also known as the minimum absolute deviation or MAD criterion) were applied to a simple linear regression model to minimize
what are the values of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] for the sales data pairs
-
1.9 Write a Monte Carlo simulation experiment that uses the same parameters as those in Example 1.4 (that is, [latex]\beta_0 = 1[/latex], [latex]\beta_1 = 1 / 2[/latex], [latex]\varepsilon \sim U(-1,1)[/latex], [latex]n = 10[/latex]) for 5000 replications, but this time selects the independent variable values to be equally likely integers from [latex]-5[/latex] and 5. Produce analogous figures to those of Figure 1.11 and Figure 1.12. Comment on your figures and how they relate to the variance–covariance matrix from Theorem 1.4.
-
1.10 For a simple linear regression model with [latex]X_{1} = 1, X_{2} = 2, \dots , X_{n} = n[/latex] and [latex]\sigma^{2} = 1[/latex] find the variance–covariance matrix of [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex].
-
1.11 Use Theorems 1.2 and 1.4 to show that the least squares estimator of the intercept of the regression line β0 in the simple linear regression model is a consistent estimator of β0.
-
1.12 Example 1.6 calculates the variance–covariance matrix for a single replication of a Monte Carlo simulation experiment. Conduct this experiment for 5000 replications and report the average of the values in the variance–covariance matrix.
-
1.13 Let L be the set of all linear estimators of the slope β1 in a simple linear regression model. Let U be the set of all unbiased estimators of the slope β1 in a simple linear regression model. Give an example of an estimator of β1 in [latex]L \cap U'[/latex].
-
1.14 Show that the fitted simple linear regression model
for [latex]i = 1, 2,\ldots, n[/latex] can be written as
where [latex]\hat{\beta}_0[/latex] and [latex]\hat{\beta}_1[/latex] are the least squares estimators of β0 and β1 and [latex]\bar{X}[/latex] and [latex]\bar{Y}[/latex] are the sample means of the observed values of the independent and dependent variables.
-
1.15 Write a paragraph that argues why a fitted least squares regression line cannot pass through all data pairs except for one of the data pairs.
-
1.16 One of the most common error distributions used in simple linear regression is the normal distribution with population mean 0 and finite population variance σ2, which has probability density function
An alternative error distribution is the Laplace distribution with probability density function
Since the error distribution must have expected value zero by assumption, this reduces to
As parameterized here, the Laplace distribution has population variance σ2. Both of these distributions are symmetric and centered about zero.
- Plot the normal and Laplace error probability density functions on [latex]-3 < x < 3[/latex] and comment on any differences between the two error distributions. Use [latex]\sigma = 1[/latex] for the plots.
- Plot the normal and Laplace error probability density functions on [latex]4 < x < 5[/latex] and comment on any differences between the tails of the two error distributions.
- Fit both of these error distributions (that is, find [latex]\hat{\sigma}^{2}[/latex] for each distribution) for the forbes data set from the MASS package in R using the simple linear regression model.
-
1.17 Let the independent variable X be a car’s speed and the dependent variable Y be the car’s stopping distance, which are going to be modeled with a simple linear regression model. In which of the following scenarios do you expect to have a larger population variance of the error term?
- The data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_{20}, Y_{20})[/latex] are [latex]n = 20[/latex] new cars that are all of the same make and model.
- The data pairs [latex](X_1, Y_1), (X_2, Y_2), \ldots, (X_{20}, Y_{20})[/latex] are [latex]n = 20[/latex] new cars from [latex]n = 20[/latex] different car manufacturers.
-
1.18 Show that the sum of squares for regression in a simple linear regression model can be written as
-
1.19 Show that the sum of squares for regression in a simple linear regression model can be written as
-
1.20 Consider the data pairs in the Formaldehyde data set built into the base R language. Use the help function in R to determine the interpretation of the independent and dependent variables. Fit a simple linear regression model to the data pairs and interpret the meaning of [latex]\hat{\beta}_0[/latex], [latex]\hat{\beta}_1[/latex], and [latex]\hat{\sigma}^{2}[/latex]. Also, calculate SST, SSR, and SSE for this data set.
-
1.21 Consider the data pairs collected by James Forbes that are given in the data frame forbes contained in the MASS package in R. The independent variable is the boiling point (in degrees Fahrenheit) and the dependent variable is the barometric pressure (in inches of mercury). For a simple linear regression model, calculate
- the fitted values,
- the residuals,
- the sum of squares for error, and
- the mean square error
without using the lm function. Then use the lm function to check the correctness of the values that you calculate.
-
1.22 This exercise investigates the effect of controllable values of [latex]X_{1}, X_{2}, \dots , X_{n}[/latex] on the coefficient of determination R2 in simple linear regression. Consider the simple linear regression model
where
- the population intercept is [latex]\beta_{0} = 1[/latex],
- the population slope is [latex]\beta_{1} = 1 / 2[/latex], and
- the error term [latex]\varepsilon[/latex] has a [latex]N(0,1)[/latex] distribution.
Conduct a Monte Carlo simulation with 40,000 replications that estimates the expected coefficient of determination for [latex]n = 10[/latex] data pairs under the following two ways of setting the values of [latex]X_{1}, X_{2}, \dots , X_{10}[/latex].
- Let [latex]X_{i} = i[/latex] for [latex]1, 2, \dots, 10[/latex].
- Let [latex]X_{1} = X_{2} = \cdots = X_{5} = 5[/latex] and [latex]X_{6} = X_{7} = \cdots = X_{10} = 6[/latex].
-
1.23 Let SX and SY be the sample standard deviations of the independent and dependent variables, respectively. Show that the following four definitions of the coefficient of correlation are equivalent.

