Chapter 4 Probability Models in Survival Analysis
One of the central aspects of survival analysis is the investigation of the probability distribution of a random variable T which has nonnegative support. In some settings, there are covariates that influence the probability distribution of T. In addition, the data collected on the random variable T is often right censored, which means that only a lower bound is available on the value of T. So there is a bit of a mental adjustment that needs to be made from probability theory, where X is usually used to denote a random variable, to survival analysis, where T is used to denote a random variable that can only assume nonnegative values. The choice of T is made because the random variable of interest is typically time. This chapter introduces probability models for T.
Four lifetime distribution representations that are commonly used to define the probability distribution of a random variable T are introduced in this chapter: the survivor function, the probability density function, the hazard function, and the cumulative hazard function. These four representations apply to both continuous (for example, the lifetime of a light bulb) and discrete (for example, the lifetime of the landing gear on an airplane) lifetimes. The survival time distribution of a drill bit, an automobile, a cat, and a recession are vastly different. One would certainly not want to use the same failure time distribution with identical parameters to model these diverse lifetimes. This chapter surveys two probability distributions (the exponential distribution as an example of a one-parameter distribution and the Weibull distribution as an example of a two-parameter distribution) that are commonly used to model lifetimes. The exponential distribution is central to survival analysis just as the normal distribution is central to classical statistics. After sections that survey other lifetime distributions and moment ratio diagrams, the Cox proportional hazards model is introduced. The proportional hazards model is appropriate for incorporating a vector of covariates that influence survival (for example, the turning speed and feed rate for a drill bit) into a lifetime model.
4.1 Lifetime Distribution Representations
The application areas associated with the probability distribution of the nonnegative random variable T are quite wide.
- In reliability engineering, T is typically the lifetime of a component or a system of components. Examples include the lifetime of a light bulb or the lifetime of a tennis racket.
- In biostatistics, T is typically the survival time of a patient. To be more specific, this might be the survival time of a patient after a particular type of surgery. More generally, the lifetime T could be the time between the end of radiation treatment for a particular cancer and the time the cancer recurs. In other words, T is the remission time.
- In actuarial science, T is often the lifetime of an insured individual in the life insurance industry. On the casualty and property side of actuarial science, T is often the lifetime of a structure or a vehicle.
- In sociology, T can model the duration of a strike, the duration of a marriage, or the duration of a business partnership. More generally, T might model the social distance between two strangers having a conversation.
- In economics, T can be the time between recessions or the absolute change in a stock market index from one year to the next.
- In systems engineering, T could be the length of time that it takes to screen a passenger at an airport. The time that a customer spends in a slow-moving queue before exiting the queue is another nonnegative random variable that might be of interest.
- In public policy, T could be the response time by emergency vehicles to a reported building fire. Alternatively, T could be the time for a released inmate to return to prison in a recidivism application within the criminal justice system.
- In library science, T could be the time that a book is checked out. The time between an interlibrary loan request and its fulfillment is another nonnegative random variable of interest to librarians.
- In meteorology, T could be the time between the formation of a tropical storm and the time it makes landfall. The time that a severe hurricane spends as a Category 5 hurricane is another nonnegative random variable of interest to meteorologists.
- In chemistry, T could be the length of time required to complete a chemical reaction. A chemist could also use T to denote the bond length between two atoms.
The long list given above is intended to highlight that survival analysis is a field that has a very wide range of applications. Although the letter T has been selected because it most often represents time, there are many applications in which it represents something other than time (for example, social distance or bond length).
When T represents time, T can be thought of as the time between two events. For this reason, this part of survival analysis is often referred to as time-to-event modeling. The time of purchase and the time of failure, for example, might be the two events for a manufactured product. Since the applications of survival analysis are wide, we will use the generic terms “failure” of an “item” when referring to the second of the two events.
This section introduces four functions that define the probability distribution of a continuous, nonnegative random variable T, the lifetime of an item. The four representations presented in this chapter are not the only ways to define the distribution of T. Other methods include the moment generating function [latex]E\left[ e^{\kern 0.04em sT} \right][/latex], the characteristic function [latex]E\left[ e^{\kern 0.04em isT} \right][/latex], the Mellin transform [latex]E\left[ T^s \right][/latex], the mean residual life function [latex]E[ T - t \, | \, T \ge t][/latex], and the reversed failure rate [latex]f(t) / F(t)[/latex]. The four representations used here have been chosen because of their intuitive appeal, usefulness in problem solving, and popularity in the literature.
4.1.1 Survivor Function
The first lifetime distribution representation is the survivor function [latex]S(t)[/latex]. The survivor function is the probability that an item is functioning at any time t.
A survivor function is also known as the reliability function [because [latex]S(t)[/latex] is the reliability of an item at time t] and the complementary cumulative distribution function [because [latex]S(t)= 1 - F(t)[/latex] for continuous random variables, where [latex]F(t) = P(T \le t)[/latex] is the cumulative distribution function]. All survivor functions must satisfy three conditions:
There are two interpretations of the survivor function. First, [latex]S(t)[/latex] is the probability that an individual item is functioning at time t. Second, if there is a large population of items with identically distributed lifetimes, [latex]S(t)[/latex] is the expected fraction of the population that is functioning at time t.
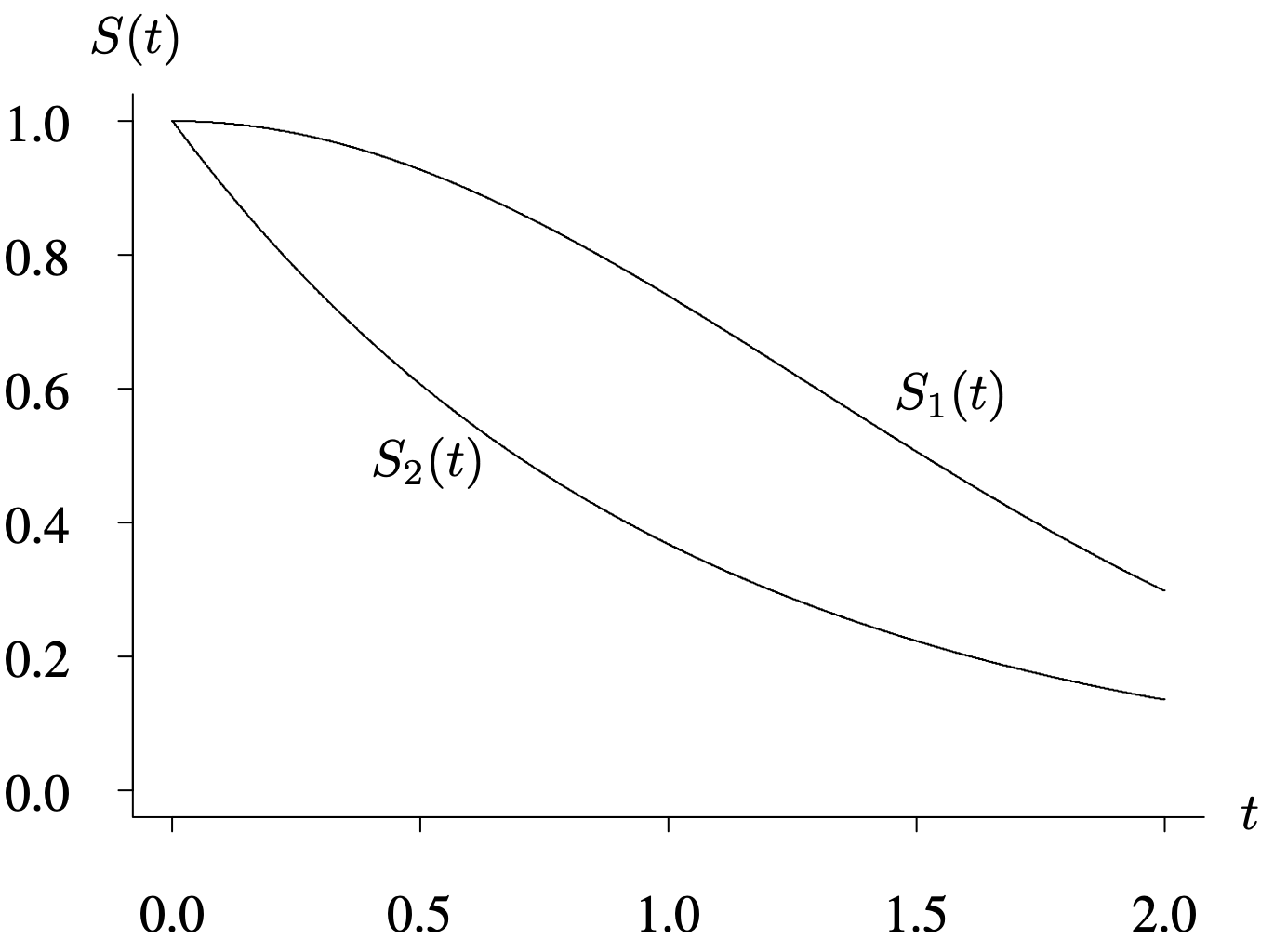
The survivor function is useful for comparing the survival patterns of several populations of items. The graph in Figure 4.1 shows survivor functions [latex]S_1 (t)[/latex] and [latex]S_2 (t)[/latex], where [latex]S_1 (t)[/latex] corresponds to population 1 and [latex]S_2 (t)[/latex] corresponds to population 2. Since [latex]S_1 (t) \ge S_2 (t)[/latex] for all t values, it can be concluded that the items in population 1 are superior to those in population 2 with regard to survival.
Long Description for Figure 4.1
The horizontal axis ranges from 0 to 2 in increments of 0.5. The vertical axis ranges from 0 to 1 in increments of 1. Survivor function 1 follows a concave down, decreasing trend, starting at (0.0, 1) and ending at (2, 0.4). The survivor function 2 follows a concave up, decreasing trend, starting at (0.0, 1) and ending at (2, 0.2).
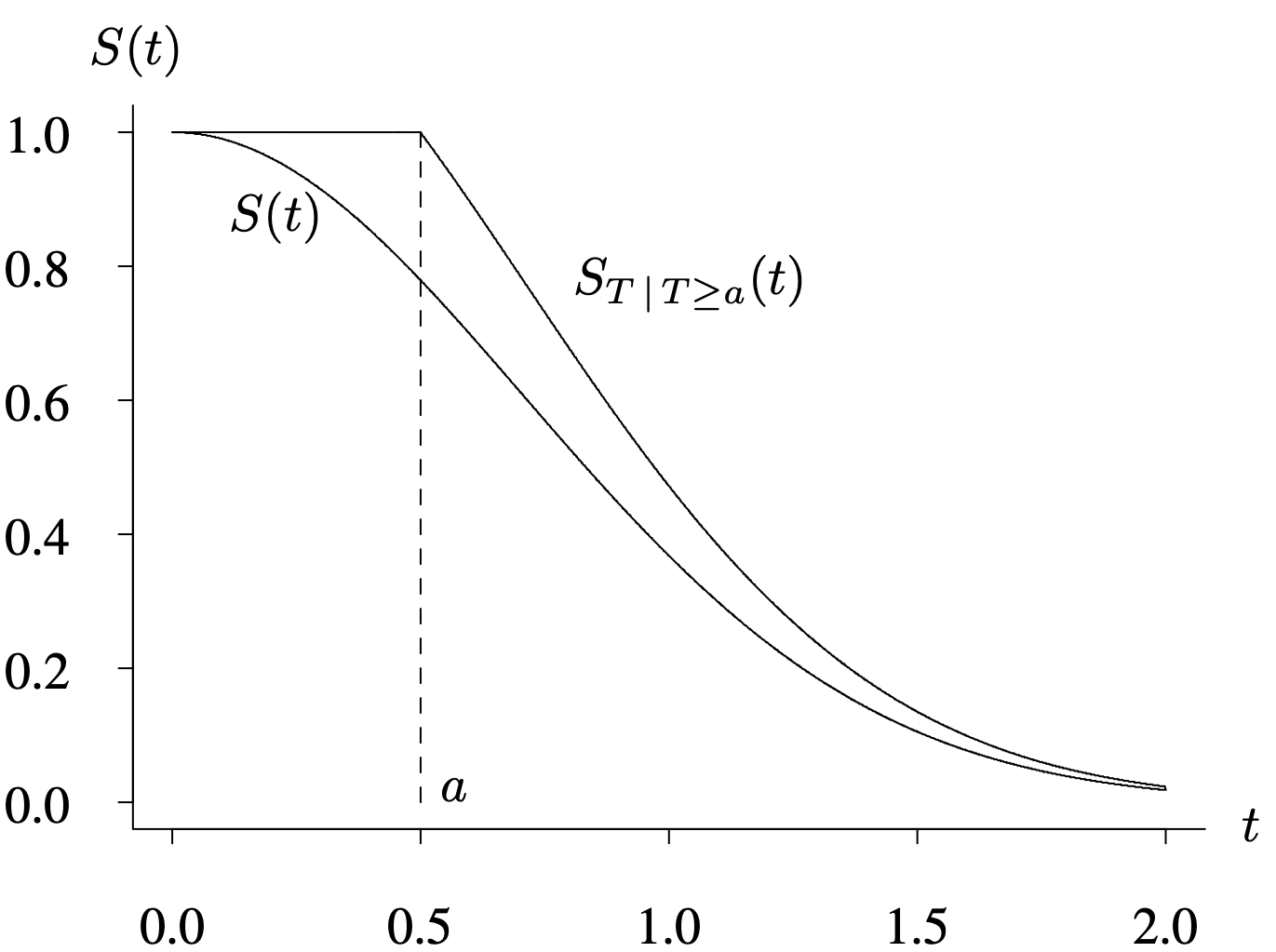
The conditional survivor function, [latex]S_{{T\,|\,T} \,\ge\, a} (t)[/latex], is the survivor function of an item that is functioning at time a:
Figure 4.2 shows the original survivor function [latex]S(t)[/latex] and the conditional survivor function [latex]S_{{T} \,|\, T \,\ge\, a} (t)[/latex] when a = 0.5. Since the conditional survivor function is rescaled by the factor [latex]S(a)[/latex], it has the same shape as the remaining portion of the original survivor function. The conditional survivor function is useful for comparing the survival experience of a group of items that has survived to time a. Examples include manufactured items surviving a burn-in test and cancer patients surviving 5 years after diagnosis and treatment. The conditional survivor function is of particular interest to actuaries. If a 37-year-old woman, for example, is purchasing a one-year term life insurance policy, an estimate of [latex]S_{{T} \,|\, T \,\ge\, 37} (38)[/latex] is required to determine an appropriate premium for the policy.
Long Description for Figure 4.2
The horizontal axis ranges from 0 to 2 in increments of 0.5. The vertical axis ranges from 0 to 1 in increments of 0.2. The original survivor function follows a concave down, decreasing trend until (1.5, 0.12 )and then inflates and then stabilizes to end at (2, 0.0). The conditional survivor function follows the same trend as that of original survivor function but starts at (0.5, 1) and then increases to (1.5, 1), and ends at (2, 0). A dotted horizontal line extends from the starting point of the conditional survivor curve to 0.5 on the X axis. A horizontal line measures the distance between the starting point of the two curves.
4.1.2 Probability Density Function
The second lifetime distribution representation is the familiar probability density function, which is defined as the negative of the derivative of the survivor function.
The probability density function has the probabilistic interpretation
for small [latex]\Delta \kern 0.02em t[/latex] values. Although the probability density function is not as effective as the survivor function for comparing the survival patterns of two populations, a graph of [latex]f(t)[/latex] indicates the likelihood of failure for any t. The probability of failure between times a and b is calculated by an integral:
All probability density functions for lifetimes must satisfy two conditions:
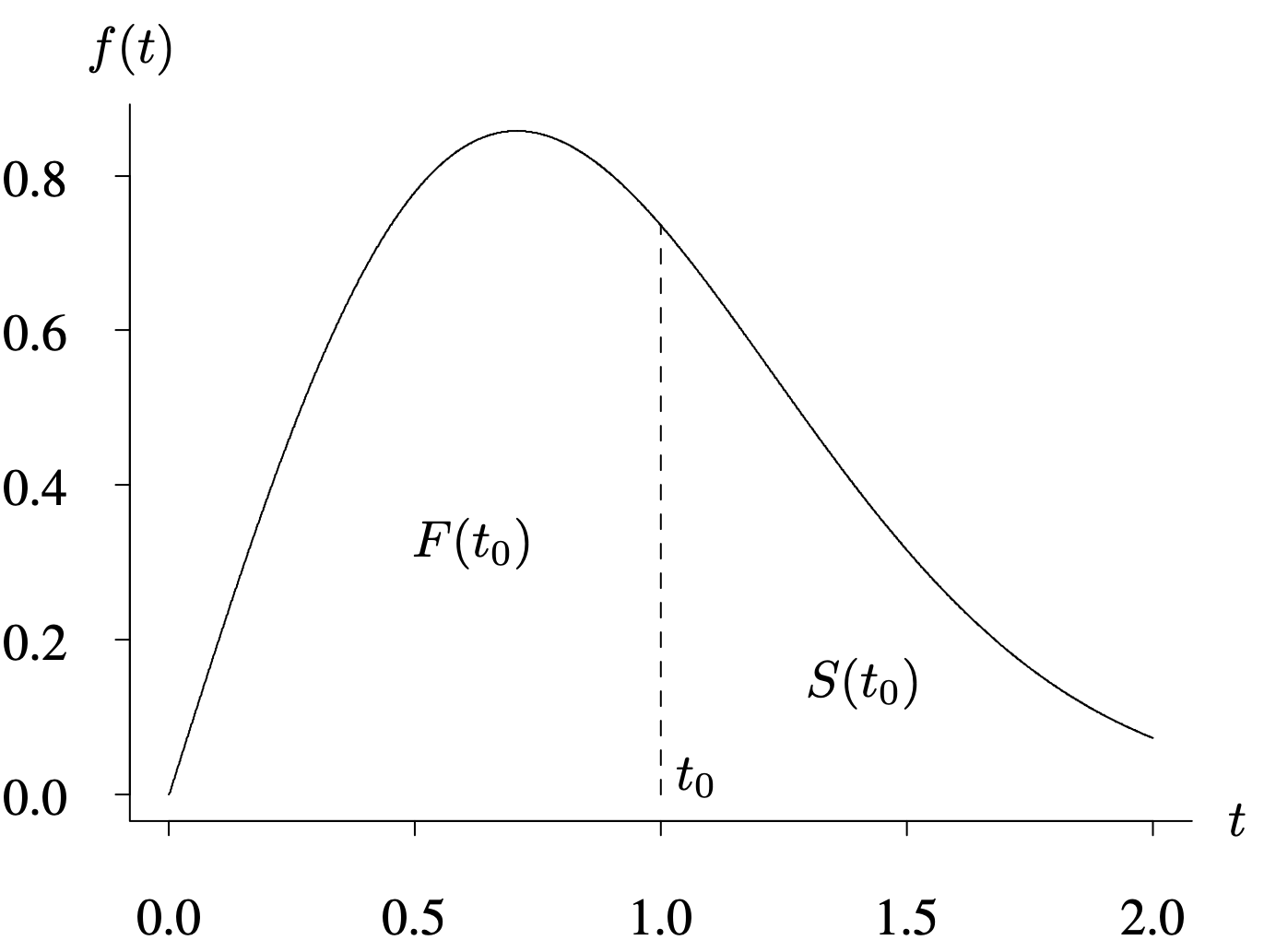
It is assumed that [latex]f(t) = 0[/latex] for all [latex]t < 0[/latex], which is consistent with our assumption that the random variable T is nonnegative. This assumption excludes distributions with negative support, such as the normal distribution. The probability density function shown in Figure 4.3 illustrates the relationship between the cumulative distribution function [latex]F(t)[/latex] and the survivor function [latex]S(t)[/latex] for a continuous lifetime. The area under [latex]f(t)[/latex] to the left of the arbitrary time [latex]t_0[/latex] is [latex]F( t_0 )[/latex]; the area under [latex]f(t)[/latex] to the right of [latex]t_0[/latex] is [latex]S ( t_0 )[/latex].
Long Description for Figure 4.3
The horizontal axis ranges from 0 to 2 in increments of 0.5. The vertical axis ranges from 0 to 0.8 in increments of 0.2. The curve starts at (0, 0), peaks at (0.7, 0.8) and drops to (2, 0.1). A dotted line from point (1, 0.7) to the horizontal axis divides the area under the curve into two portions. The region on the left is labeled, F of t subscript 0, and the region on the right is labeled, S of t subscript 0.
4.1.3 Hazard Function
The hazard function, [latex]h(t)[/latex], is perhaps the most popular of the four representations for survival analysis due to its intuitive interpretation as the amount of risk associated with an item at time t. A second reason for its popularity is its usefulness in comparing the way risks change over time for several populations of items by plotting their hazard functions on a single axis. A third reason is that the hazard function is a special case of the intensity function for a nonhomogeneous Poisson process, which will be introduced in a subsequent chapter. A hazard function models the occurrence of one event, a failure, whereas the intensity function models the occurrence of a sequence of events over time. The hazard function goes by several aliases: in reliability it is also known as the hazard rate or failure rate; in actuarial science it is known as the force of mortality or force of decrement; in point process and extreme value theory it is known as the rate or intensity function; in vital statistics it is known as the age-specific death rate; and in economics its reciprocal is known as Mill’s ratio.
The hazard function can be derived using conditional probability. First, consider the probability of failure between t and [latex]t + \Delta \kern 0.02em t[/latex]:
Conditioning on the event that the item is working at time t yields
If this conditional probability is averaged over the interval [latex][t,\ t + \Delta \kern 0.02em t ][/latex] by dividing by [latex]\Delta \kern 0.02em t[/latex], an average rate of failure is obtained:
As [latex]\Delta \kern 0.02em t \to 0[/latex], this becomes the instantaneous failure rate, which is the hazard function
using the definition of the derivative from calculus. This forms the basis for the following definition.
Thus, the hazard function is the ratio of the probability density function to the survivor function. Using the previous derivation, a probabilistic interpretation of the hazard function is
for small [latex]\Delta \kern 0.02em t[/latex] values, which is a conditional version of the interpretation for the probability density function. All hazard functions must satisfy two conditions:
The units on a hazard function are typically given in failures per unit time. In Example 4.1, if [latex]{\lambda = 0.01}[/latex], [latex]{\kappa = 1}[/latex], and time is measured in hours, then [latex]h(t)[/latex] = 0.01 failures per hour. Manufactured items are often so reliable that to avoid hazard functions such as [latex]h(t)[/latex] = 0.00000128 failures per hour the units are changed so that the hazard function may be expressed as [latex]h(t)[/latex] = 1.28 failures per 106 hours. Another way to avoid writing too many leading zeroes is to change the units to years, where one year equals 8760 hours.
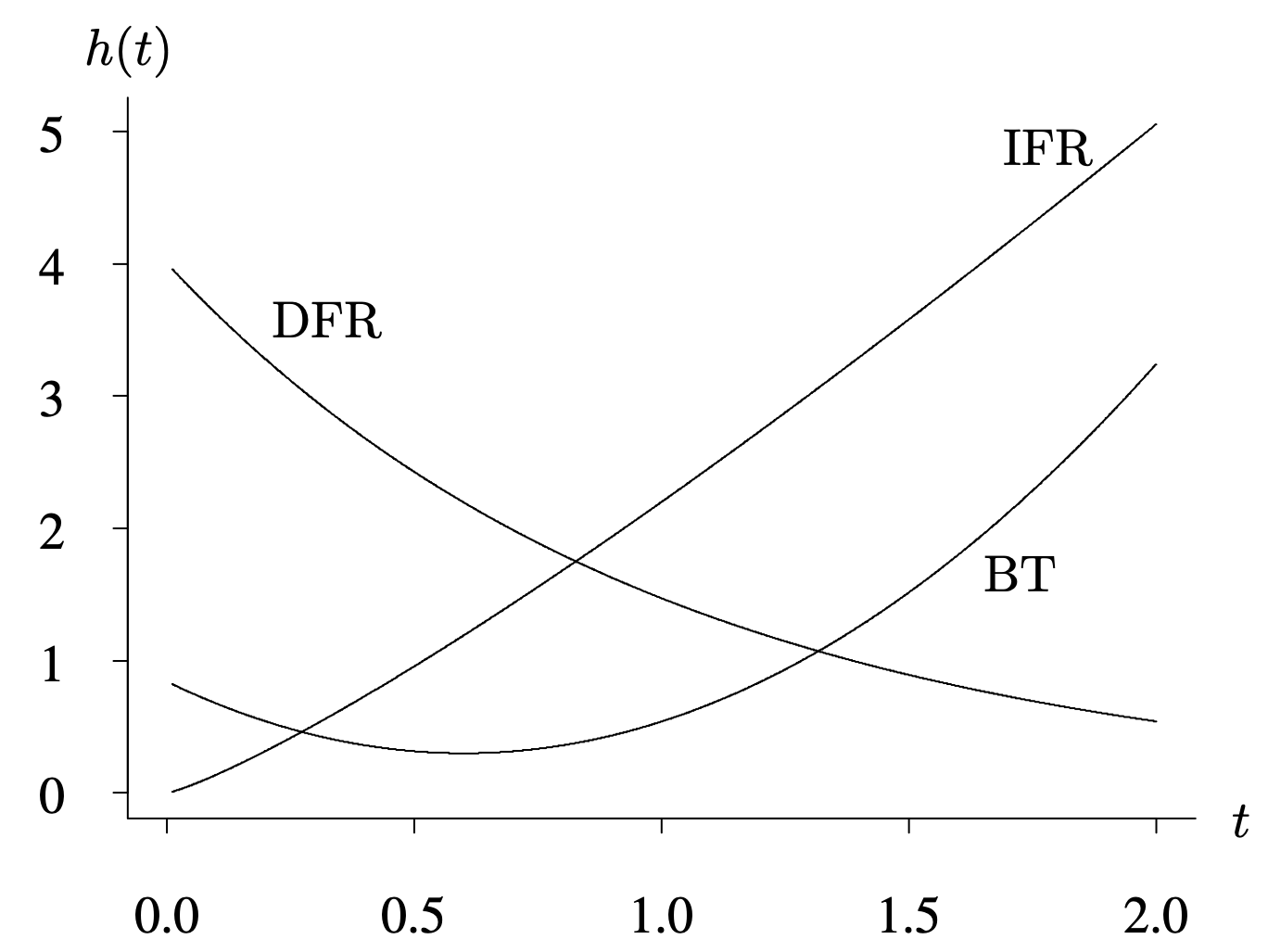
The shape of the hazard function indicates how an item ages. The intuitive interpretation of [latex]h(t)[/latex] as the amount of risk an item is subject to at time t implies that when the hazard function is larger the item is under greater risk of failure, and when the hazard function is smaller the item is under less risk of failure. The three hazard functions plotted in Figure 4.5 correspond to an increasing hazard function (labeled IFR for increasing failure rate), a decreasing hazard function (labeled DFR for decreasing failure rate), and a bathtub-shaped hazard function (labeled BT for bathtub-shaped failure rate).
Long Description for Figure 4.5
The horizontal axis, X indicating t, ranges from 0.0 to 2.0 in increments of 0.5. The vertical axis, Y indicating h of t, ranges from 0 to 5 in increments of 1. D F R is a decreasing curve, starting from (0,4) and ending at (2,1). B T is a bathtub shaped curve, starting at (0,1) and dipping at (0.7, 0.1) and the increasing to (2, 3). I F R is an increasing curve, starting at (0,0) and increasing steadily to (2, 5).
The increasing hazard function is probably the most common situation of the three depicted in Figure 4.5. In this case, items are more likely to fail as time passes. In other words, items wear out or degrade with time. This is almost certainly the case with mechanical items that undergo wear or fatigue. It can also be the case in certain biomedical experiments. Let T, for example, be the time until a tumor appears after the injection of a substance into a laboratory animal. If the substance makes the tumor more likely to appear as time passes, then the hazard function associated with T is increasing. This leads to the formal definition of the IFR class. Notice the loose use of the term increasing in the definition of the IFR class (because IFR distributions have nondecreasing hazard functions).
The second situation depicted in Figure 4.5, the decreasing hazard function, is less common. In this case, the item is less likely to fail as time passes. Items with this type of hazard function improve with time. Some metals work-harden through use and thus have increased strength as time passes. Another situation for which a decreasing hazard function might be appropriate for modeling is in working bugs out of computer programs. Bugs are more likely to appear initially, but the likelihood of them appearing decreases as time passes. This leads to the formal definition of the DFR class.
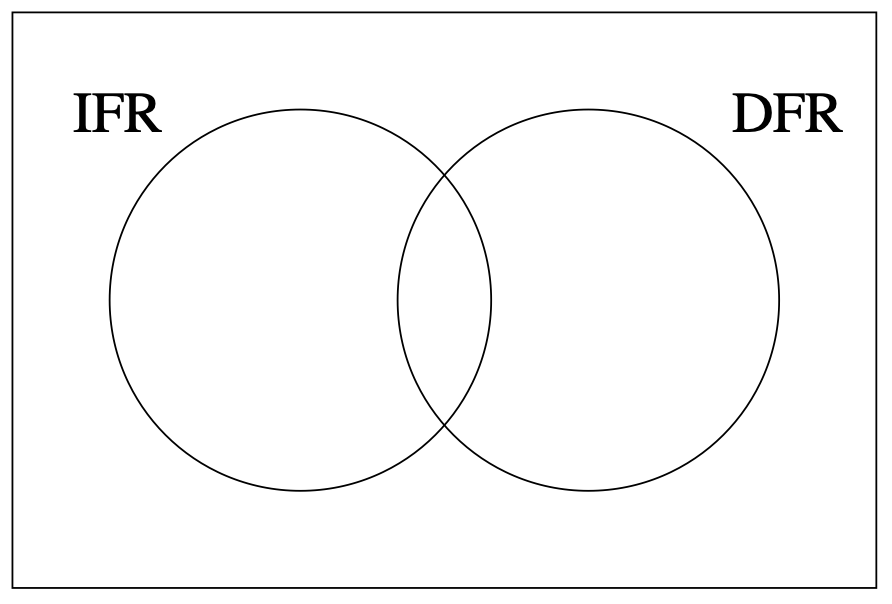
The loose use of the term increasing in the definition of the IFR class and the term decreasing in the definition of the DFR class allows a distribution with a constant hazard function, the exponential distribution, to serve as a boundary between the two classes. The exponential distribution’s hazard function [latex]h(t) = \lambda[/latex] for [latex]t \ge 0[/latex], is both nondecreasing and nonincreasing, so it belongs to both the IFR and DFR classes. As shown in the Venn diagram in Figure 4.6, this definition of IFR and DFR classifies all lifetime distributions into one of four sets: a constant hazard function (that is, the exponential distribution, which is the intersection of the IFR and DFR classes), strictly increasing hazard functions, strictly decreasing hazard functions, and other hazard functions (such as bathtub-shaped hazard functions).
The third situation depicted in Figure 4.5, a bathtub-shaped hazard function, occurs when the hazard function decreases initially and then increases as items age. Items improve initially and then degrade as time passes. One situation in which the bathtub-shaped hazard function arises is in the lifetimes of manufactured items. Often manufacturing, design, or component defects cause early failures. The period in which these failures occur is sometimes called the burn-in period. If failure is particularly catastrophic, this part of the lifetime will often be consumed by the manufacturer in a controlled environment. The time value during which early failures have been eliminated may be valuable to a producer who is determining an appropriate warranty period. Once items pass through this early part of their lifetime, they have a fairly constant hazard function, and failures are equally likely to occur at any point in time. Finally, as items continue to age, the hazard function increases, resulting in wear-out failures. The three paragraphs that follow give examples of applications of the bathtub-shaped hazard function.
The bathtub-shaped hazard function can be envisioned for calculators; the burn-in period corresponds to the first few weeks of use when manufacturing, design, or component defects arise. Wear-out failures occur after a few years of use when the buttons are about ready to fall off. Failures due to calculators being dropped occur throughout the life of a calculator. If these failures are equally likely at any time, the hazard function will be increased by a constant that reflects the probability of dropping the calculator for all time values.
The bathtub-shaped hazard function also arises in the lifetimes of people. In this case, the early failures are known as infant mortality deaths and occur during the first few years of life. After this time, the hazard function has a very gentle increase through the teenage years and into adulthood. Finally, old age deaths occur during the later years of life. The magnitude of the hazard function depends on factors such as the standard of living and medical services available. Also, occupation (for example, flower arranger versus stunt man) and lifestyle (for example, eating habits, sleeping habits, smoking habits, stress level) affect the lifetime distribution of a person. The hazard function is used in actuarial science; the appropriate premium for a life insurance policy is based on probabilities associated with the lifetime distribution. The lowest life insurance premiums are usually for children who have survived the infant mortality part of their lifetimes.
There are dozens of other lifetime distribution classes beyond just the IFR and DFR classes. These include IFRA (increasing failure rate on average), DFRA (decreasing failure rate on average), IMRL (increasing mean residual life), and DMRL (decreasing mean residual life).
Care must be taken to differentiate between the hazard function for a population and the hazard function for an individual item under consideration. To use human lifetimes as an illustration, consider the following question: do two healthy 11-year-old boys living in the same town necessarily have the same hazard function? The answer is no. The reason is that all people are born with genetic predispositions that will influence their risk as they age. So, although a hazard function exists for all 11-year-old boys living in that particular town, it is an aggregate hazard function representing the population, and individual boys may be at increased or decreased risk. This is why life insurance companies typically require a medical exam to determine whether an individual is at higher risk than the rest of the population. The common assumption in most probabilistic models and statistical analyses is that of mutually independent and identically distributed random variables, which in this case are lifetimes. This assumption is not always valid in survival analysis applications because items are often manufactured in diverse conditions (for example, different temperatures or raw materials).
4.1.4 Cumulative Hazard Function
The fourth lifetime distribution representation, the cumulative hazard function, is defined as the integral of the hazard function.
Whereas the hazard function reflects the risk pattern associated with an item over time, the cumulative hazard function gives the accumulated risk at time t. Similar to the way a cumulative distribution function accumulates probability, the cumulative hazard function [latex]H(t)[/latex] accumulates the risk from time 0 to time t. All cumulative hazard functions must satisfy three conditions:
The cumulative hazard function is valuable for random variate generation in Monte Carlo simulation, implementing certain procedures in statistical inference, and defining certain distribution classes (for example, the IFRA class).
The four lifetime distribution representations presented here are equivalent in the sense that each completely specifies a lifetime distribution. In addition, any one lifetime distribution representation implies the other three. Algebra and calculus can be used to find one lifetime distribution representation given that another is known. For example, if the survivor function is known, the cumulative hazard function can be determined by
where [latex]ln[/latex] is the natural logarithm ([latex]log[/latex] base e). The from–to matrix in Table 4.1 shows that any of the three other lifetime distribution representations (given by the columns) can be found if one of the representations (given by the rows) is known. It is assumed that the support of the lifetime T is [latex][0, \, \infty)[/latex] in Table 4.1.
|
[latex]f(t)[/latex] |
[latex]S(t)[/latex] |
[latex]h(t)[/latex] |
[latex]H(t)[/latex] |
|
|---|---|---|---|---|
|
[latex]f(t)[/latex] |
[latex]\bullet[/latex] |
[latex]\displaystyle{\int _ t ^{\infty} \kern -0.1em f( \tau ) d \tau}[/latex] |
[latex]{ \displaystyle{f(t)} \over {\displaystyle{\int _ t ^ \infty f( \tau ) d \tau}} }[/latex] |
[latex]\displaystyle{- \kern -0.0em \ln \left[ \int _ t ^ \infty \kern -0.0em f( \tau ) d \tau \kern -0.0em \right]}[/latex] |
|
[latex]S(t)[/latex] |
[latex]\displaystyle -S^{\kern 0.04em \prime}(t)[/latex] |
[latex]\bullet[/latex] |
[latex]\displaystyle {{-S^{\kern 0.04em \prime}(t)} \over {S(t)}}[/latex] |
[latex]-\ln \, S(t)[/latex] |
|
[latex]h(t)[/latex] |
[latex]h(t) \, e ^ {-\int _ 0 ^ t h(\tau) d \tau}[/latex] |
[latex]e ^ {-\int _ 0 ^ t h( \tau ) d \tau}[/latex] |
[latex]\bullet[/latex] |
[latex]\displaystyle \int _ 0 ^ t h(\tau) d \tau[/latex] |
|
[latex]H(t)[/latex] |
[latex]H'(t) \, e ^ {-H(t)}[/latex] |
[latex]e ^ {-H(t)}[/latex] |
[latex]H'(t)[/latex] |
[latex]\bullet[/latex] |
4.2 Exponential Distribution
Just as the normal distribution plays a pivotal role in classical statistics because of the central limit theorem, the exponential distribution plays a pivotal role in survival analysis because it is the only continuous distribution with a constant hazard function. The exponential distribution has a single positive scale parameter λ, often called the failure rate by reliability engineers.
The four lifetime distribution representations are plotted in Figure 4.7 for [latex]\lambda = 1[/latex] and [latex]\lambda = 2[/latex]. Two-parameter distributions, which are more complex but can model a wider variety of situations, are presented in subsequent sections.
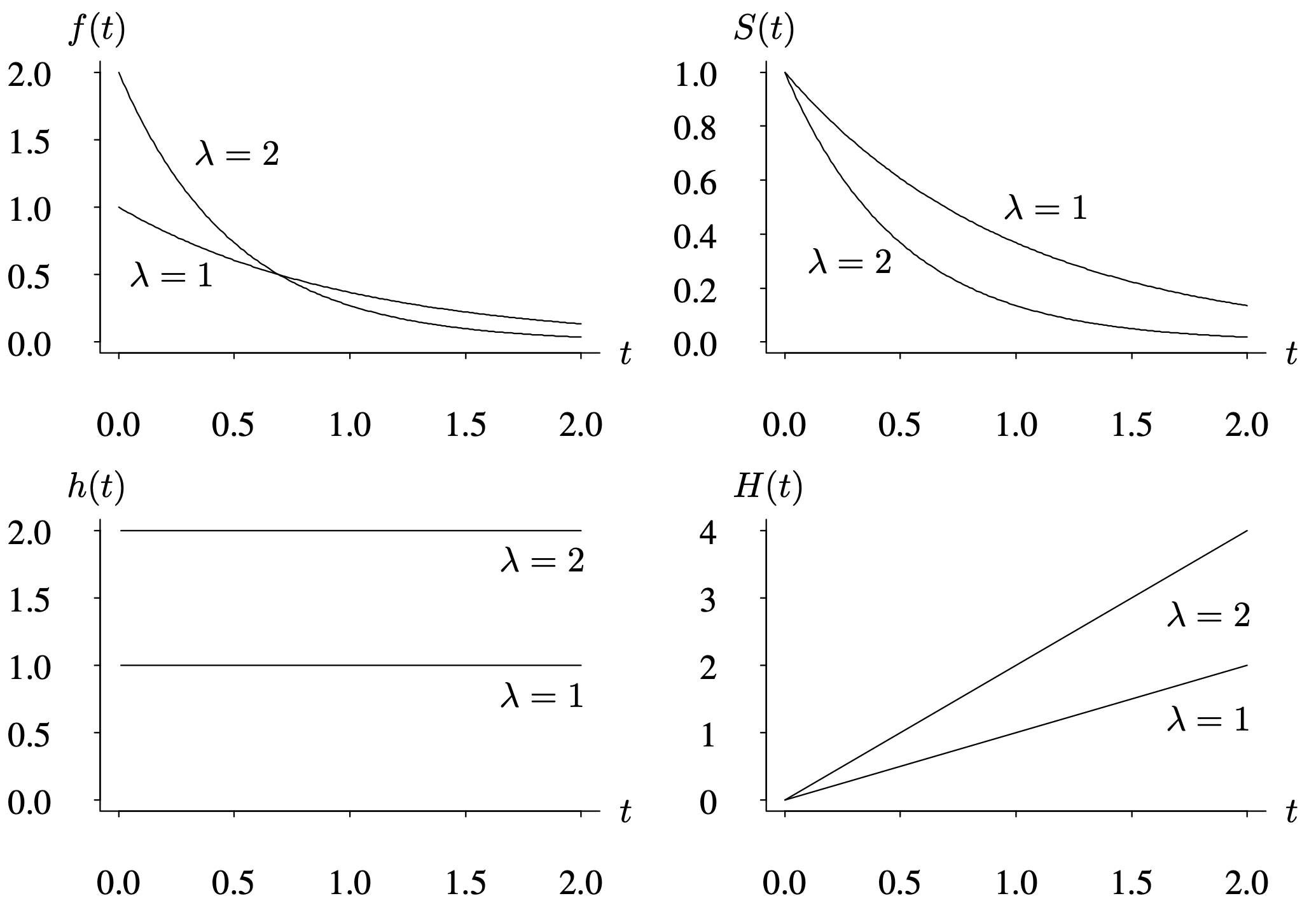
Long Description for Figure 4.7
The horizontal axis ranges from 0.0 to 2.0 in increments of 0.5. The first graph depicts t versus f of t. The vertical axis ranges from 0.0 to 2.0 in increments of 0.5. When lambda is 1, the graph shows a decreasing trend, starting from (0, 1) and ending at (2, 0). When lambda is 2, the graph follows the same trend. It decreases exponentially from (0, 2) to (2, 0). The two curves intersect at (0, 0.5). The second graph depicts t versus S of t. The vertical axis ranges from 0.0 to 1.0 in increments of 0.2. When lambda is 1, the graph shows a decreasing trend. It decreases steadily from (0, 1) to (2, 2). When lambda is 2, the graph follows the same trend. It decreases exponentially from (0, 1) to (2, 0). The third graph depicts t versus h of t. The vertical axis ranges from 0.0 to 2.0 in increments of 0.5. When lambda is 1, the graph shows a horizontal line with a constant Y value which is 1 and zero slope. When lambda is 2, the graph shows a horizontal line with a constant Y value which is 2 and zero slope. The fourth graph depicts t versus H of t. When lambda is 1, the graph shows a linear increasing trend. The line increases gradually and steadily from (0, 0) to (2, 2). When lambda is 2, the graph shows the same trend, increasing rapidly from (0, 1) to (2, 4).
The centrality, tractability, and importance of the exponential distribution make it a key probability distribution to know well. In that light, this section surveys several probabilistic properties of the exponential distribution that are useful in understanding how it is unique and when it should be applied. In all the properties, it is assumed that the nonnegative lifetime T has the exponential distribution with parameter λ.
As shown in Figure 4.8 for [latex]\lambda = 1[/latex] and s = 0.5, this result indicates that the conditional survivor function for the lifetime of an item that has survived to time s is identical to the survivor function for the lifetime of a brand new item. This used-as-good-as-new assumption is very strong. Consider, for example, whether the exponential distribution should be used to model the lifetime of a candle with an expected burning time of 5 hours. If several candles are sampled and burned, we could imagine a bell-shaped histogram for candle lifetimes, centered around 5 hours. The exponential lifetime model is certainly not appropriate in this case, because a candle that has burned for 4 hours does not have the same remaining lifetime distribution as that of a brand new candle. The exponential distribution would only be appropriate for candle lifetimes if the remaining lifetime of a used candle is identical to the lifetime of a new candle. An electrical component for which the exponential lifetime assumption might be justified is a fuse. A fuse is designed to fail when there is a power surge that causes the fuse to fail, resulting in a blown fuse which must be replaced. Assuming that the fuse does not undergo any weakening or degradation over time and that power surges that cause failure occur at a constant rate over time, the exponential lifetime assumption is appropriate, and a used fuse that has not failed is as good as a new one in terms of longevity.
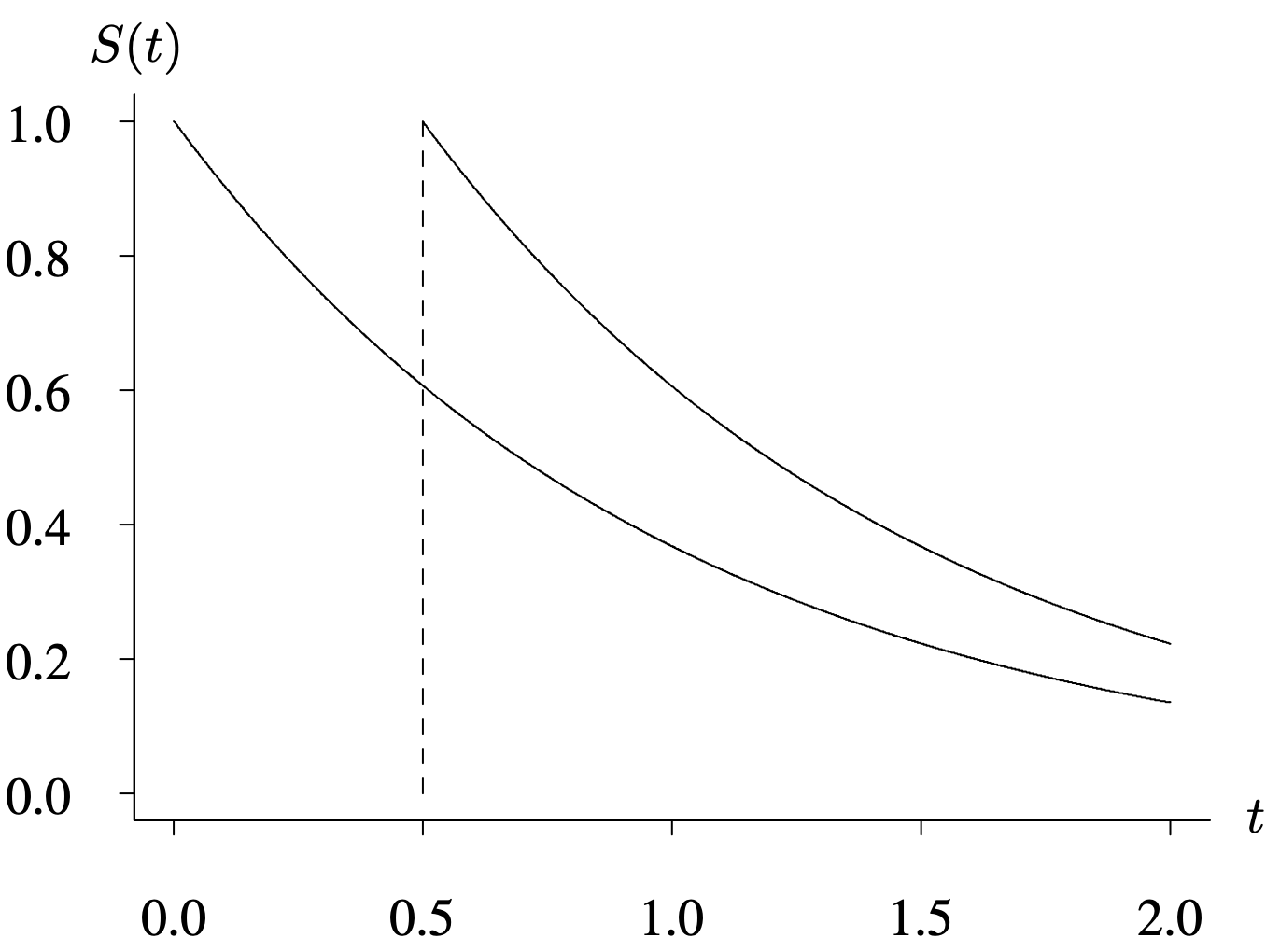
Long Description for Figure 4.8
The horizontal axis, measuring t ranges between 0 and 2.0 in increments of 0.5. The vertical axis measuring S of t ranges between 0 and 1 in increments of 0.2. A curve starting at (0, 1) passes through (0.5, 0.6); (1, 0.4); (1.5, 0.2); and (2, 0.2). The second curve starting at (0.5, 1) passes through (1, 0.7); (1.5, 0.5) and (2, 0.3). A dotted line extends from 0.5 on the horizontal axis to the starting point of the second curve.
The exponential distribution should be applied judiciously because the memoryless property restricts its applicability. It is often misapplied for the sake of simplicity because the statistical techniques for the exponential distribution are particularly tractable, or because small sample sizes do not support more than a one-parameter distribution.
The exponential distribution is the only continuous distribution with the memoryless property. The exponential distribution is the only continuous lifetime distribution for which the conditional lifetime distribution of a used item is identical to the original lifetime distribution. The only discrete distribution with the memoryless property is the geometric distribution.
This property is mathematically equivalent to the probability integral transformation, which states that [latex]F(T) \sim U(0, \, 1)[/latex], resulting in the inverse-cdf technique for generating random variates for Monte Carlo simulation: [latex]T \leftarrow F ^{{-1}} (U)[/latex], where [latex]U \sim U(0, \, 1)[/latex]. Using Theorem 4.2, random lifetime variates are generated by
because [latex]-\ln (1 - U)[/latex] is a unit exponential random variate. Random lifetimes generated in this fashion are generated by the cumulative hazard function technique.
Figure 4.9 illustrates the geometry associated with generating a variate from the cumulative hazard function. The value of [latex]- \ln (1 - U)[/latex], the unit exponential random variate, is indicated on the vertical axis, and the corresponding random variate T is indicated on the horizontal axis.
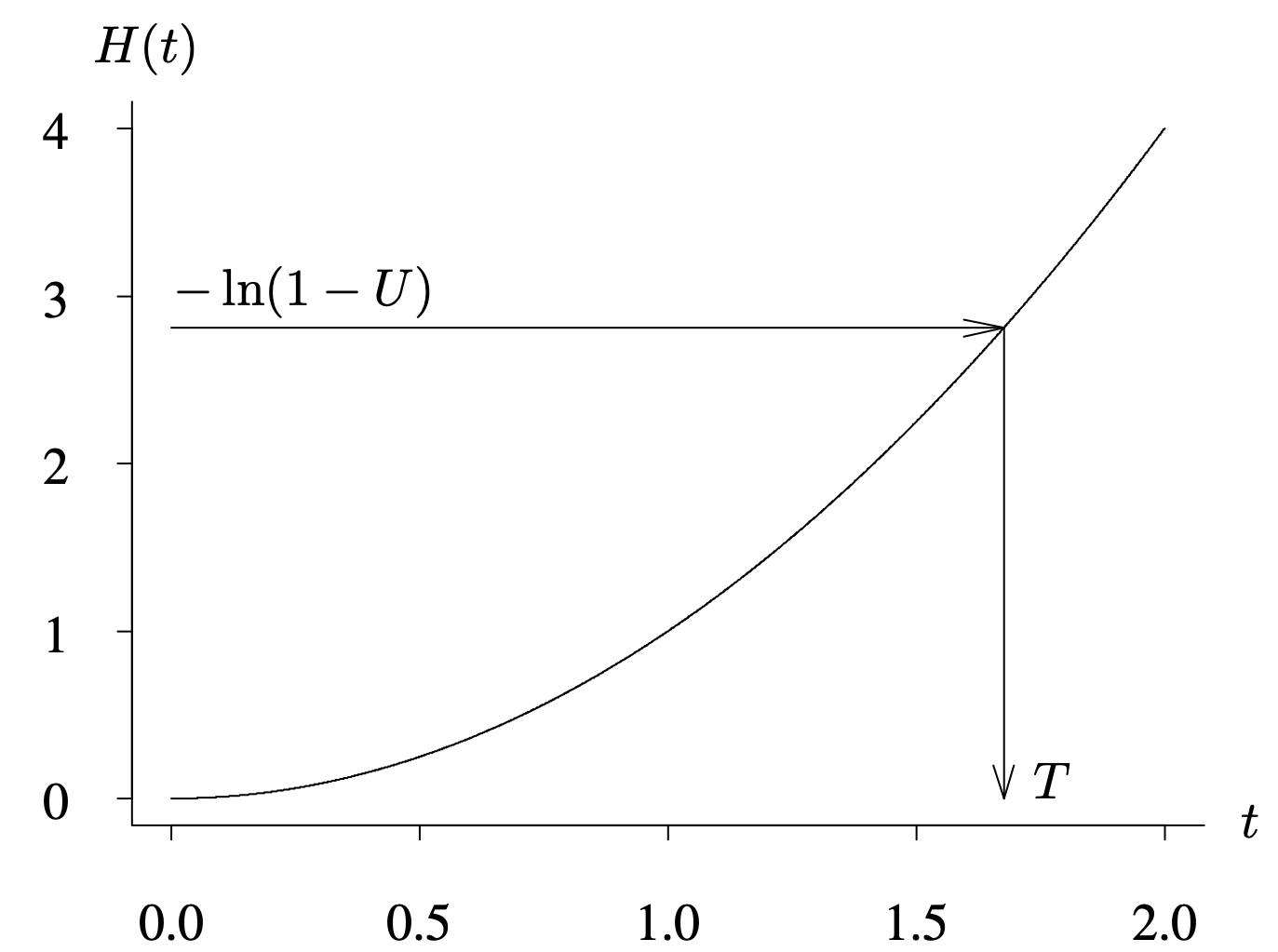
Long Description for Figure 4.9
“The horizontal axis indicating the random variate t ranges from 0.0 to 2.0 in increments of 0.5. The vertical axis indicating the unit exponential random variate ranges from 0 to 4 in increments of 1. A curve starting from points (0,0) follows an increasing trend and passes through the following points. (0.5, 0.2); (1, 0.8); (1.5, 2); (2, 3.3). The random variate corresponding to the value of unit exponential random variate 2.9 on the vertical axis, is indicated as 1.7 on the horizontal axis with marked arrows.”
The next result gives a general expression for the sth moment of an exponential random variable.
When s is a nonnegative integer, this expression reduces to [latex]E [ T^s ] = {s!} / {\lambda^s}[/latex]. By setting [latex]s = 1, 2, 3[/latex], and 4, the population mean, variance, coefficient of variation, skewness, and kurtosis can be obtained:
Since the coefficient of variation of an exponential random variable is 1, a quick check for exponentiality for a data set is to see if the ratio of the sample standard deviation to the sample mean is approximately 1. The histogram of the sample values should also have the appropriate shape.
This result indicates that the minimum of n exponential random lifetimes also has the exponential distribution. This is important in two applications. First, if n components, each with mutually independent exponential times to failure, are arranged in a series system, then the distribution of the system failure time is also exponential with a failure rate equal to the sum of the component failure rates. Second, when there are several mutually independent, exponentially distributed causes of failure competing for the lifetime of an item (for example, failing by open or short circuit for an electronic item or death by various diseases for a human being), then the lifetime can be modeled as the minimum of the individual lifetimes from each cause of failure.
This property is useful for determining a confidence interval for λ based on a data set of n mutually independent exponential(λ) lifetimes. With probability [latex]1 - \alpha[/latex],
where the left- and right-hand sides of this inequality are the [latex]\alpha / 2[/latex] and [latex]1 - \alpha / 2[/latex] fractiles of the chi-square distribution with 2n degrees of freedom. This notation is illustrated in Figure 4.10, with the three areas under the probability density function of the chi-square random variable plotted on the graph. Rearranging this expression yields an exact [latex]{100(1 - \alpha)}\%[/latex] two-sided confidence interval for λ:
$$
{\chi_{2n, \, 1 – \alpha / 2 }^2
\over 2 \displaystyle \sum_{{i \, = \, 1}}^{n} T_i} < \lambda <
{\chi_{2n, \, \alpha / 2 }^2
\over 2 \displaystyle \sum_{{i \, = \, 1}}^{n} T_i}.
$$
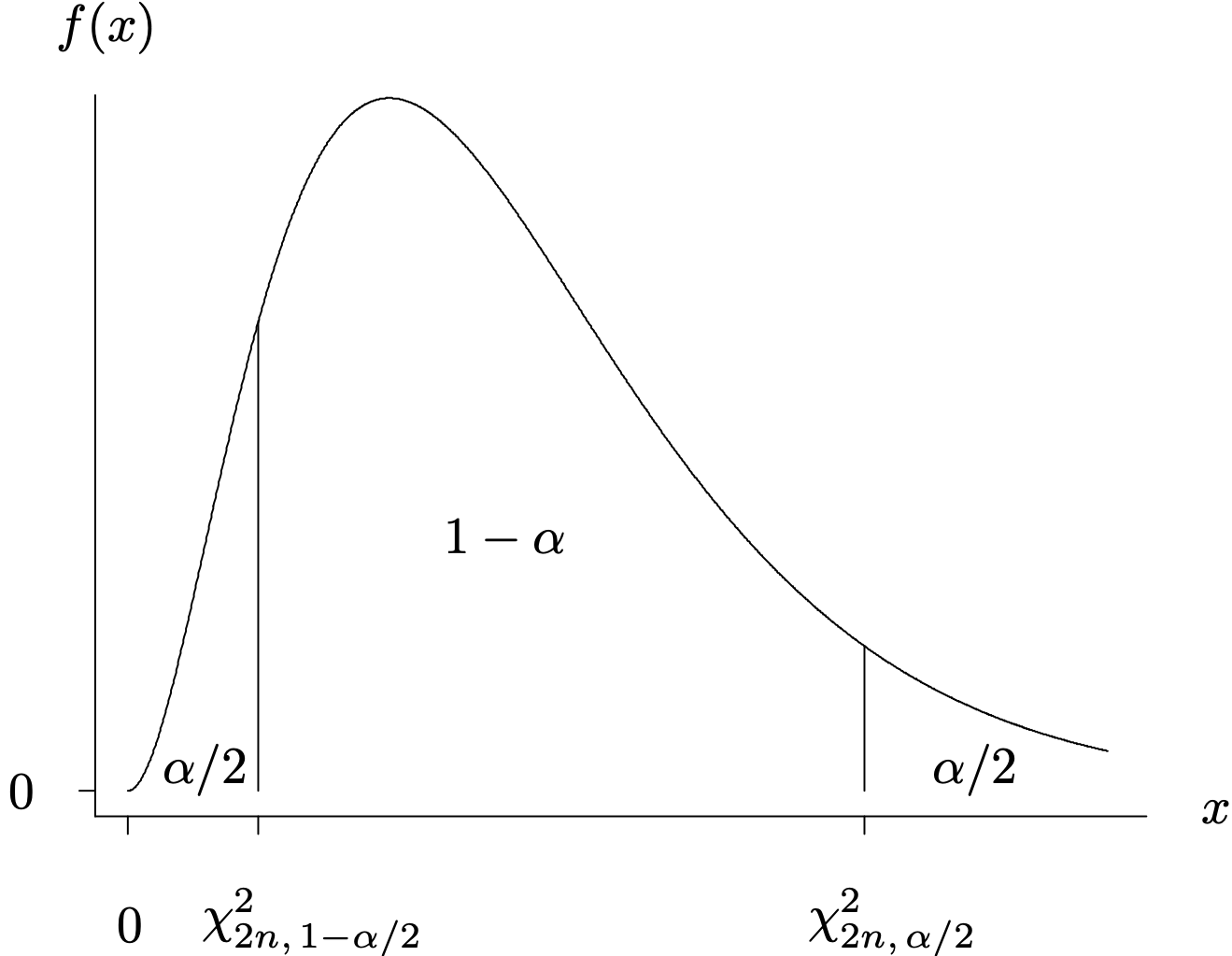
Long Description for Figure 4.10
The horizontal axis is labeled x and the vertical axis is labeled f of x. A curve originates from (0,0), peaks and drops to with a tail as it approaches the right end of horizontal axis. Two points chi squared 2 n, 1 minus alpha over two and chi squared 2 n, alpha over 2 are marked near the origin and away from the origin respectively. Two vertical lines extend from these points to the curve. The vertical lines divide the area below the curve into three regions, which are labeled alpha over 2, 1 minus alpha and alpha over 2, from left to right.
This property involves the only two probability distributions with the memoryless property. The ceiling function returns the next highest integer associated with the continuous failure time T. A modeling situation in which this property might be of interest occurs when an item with an exponential(λ) failure time distribution is placed on test at noon on a particular day. (The item could be a manufactured item such as a light bulb in the reliability setting or a subject such as a laboratory animal with cancer in a biostatistics setting.) Rather than continuously monitoring the item in order to observe its failure time T, you instead check the item for failure each subsequent day at noon. If time is measured in days, then the day number in which you observe failure is [latex]\lceil \,T\, \rceil[/latex], which the property indicates has a geometric distribution. Data collected in this fashion is known as current status data. A time to failure is known as interval censored when only a lower bound and upper bound are known on a failure time, as is the case in the scenario presented here.
The exponential distribution, for which the item under study does not age in a probabilistic sense, is the simplest of the lifetime models. Three are many other important properties of the exponential distribution in addition to those presented in this section. The two-parameter Weibull distribution, which includes the exponential distribution as a special case, is presented next. It is more flexible for modeling, although more complex mathematically.
4.3 Weibull Distribution
The exponential distribution is limited in applicability because of the memoryless property. The assumption that a lifetime has a constant failure rate is often too restrictive or inappropriate. Mechanical items, for instance, typically degrade over time and hence their lifetimes are more likely to follow a probability distribution with a strictly increasing hazard function. The Weibull distribution, named after Swedish mathematician Waloddi Weibull, is a generalization of the exponential distribution that is appropriate for modeling lifetimes having constant, strictly increasing, or strictly decreasing hazard functions.
The first four lifetime distribution representations for the Weibull([latex]\lambda, \, \kappa[/latex]) distribution are for [latex]t \ge 0[/latex], where [latex]\lambda > 0[/latex] and [latex]\kappa > 0[/latex] are the scale and shape parameters of the distribution. The hazard function approaches zero from infinity for [latex]\kappa < 1[/latex], is constant for [latex]\kappa = 1[/latex], the exponential case, and increases from zero for [latex]\kappa > 1[/latex]. One other special case occurs when [latex]\kappa = 2[/latex], commonly known as the Rayleigh distribution, which has a linear hazard function with slope [latex]2 \lambda^2[/latex]. When [latex]3 < \kappa < 4[/latex], the probability density function resembles that of a normal probability density function, and the mode and median of the distribution are equal when [latex]\kappa[/latex][latex]\cong 3.26[/latex]. The R code for plotting these lifetime distribution representations for [latex]\lambda = 1[/latex] and [latex]\kappa = 0.5, \, 1, \, 2, \, 3[/latex] is given below. The by argument in the call to the seq function controls the spacing between the t values plotted. The matplot function plots several functions on a single plot simultaneously.

These four functions are plotted in Figure 4.11 for [latex]\lambda = 1[/latex] and [latex]\kappa = 0.5, \, 1, \, 2, \, 3[/latex].
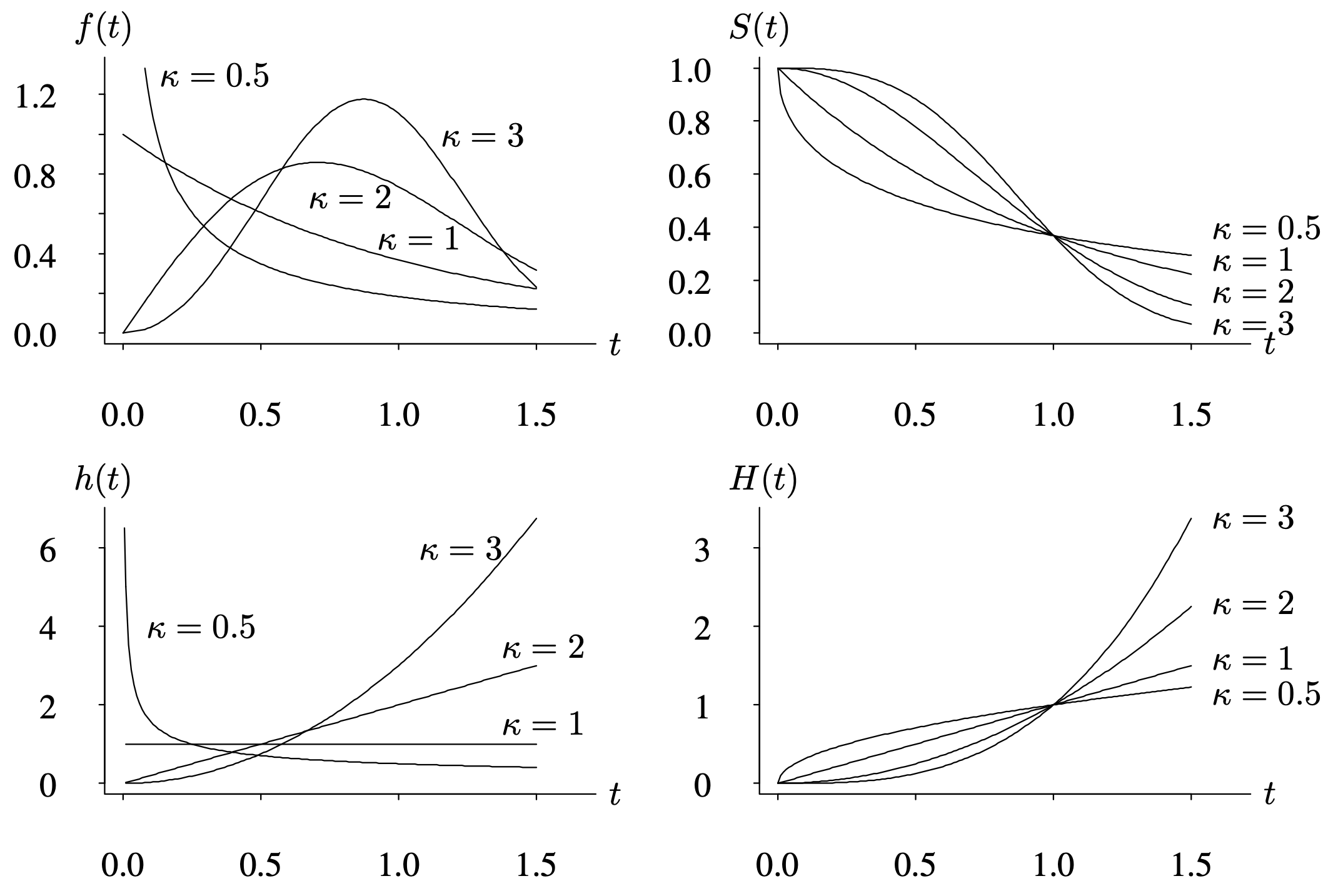
Long Description for Figure 4.11
“In each of the graphs, the horizontal axis labeled t ranges from 0 to 1.5 in increments of 0.5. Graph 1: The vertical axis labeled f of t ranges from 0 to 1.2 in increments of 0.4. The K equals 0.5 curve originating at (0,1.2) declines rapidly to reach (0.5, 0.2) and then declines gradually to reach (1.5, 0.1). The K equals 1 curve gradually declines from (0, 1.1) to (1.5, 0.2). The K equals 2 curve originating at (0,0) follows concave down increasing trend, reaches peak at (0.7, 0.8) and drops to (1.5, 0.4). The K equals 3 curve is bell-shaped starting at (0,0). It peaks at (1, 1.2) and drops to (1,5, 0.2). All data are approximate. Graph 2: The vertical axis labeled S of t ranges from 0 to 1 in increments of 0.2. The K equals 0.5 curve declines from (0,1) to (1, 0.4) and ends at (1.5, 0.4). The K equals 1 curve decreases from (0,1) to (1.5, 0.4). The K equals 2 curve decreases follows an inverse S-shape. It starts from (0,1), inflects at (1.0, 0.4) and ends in (1.5, 0.1). The K equals 3 curve also follows an inverse S -shape. It starts from (0,1), inflects at (1, 0.40 and ends in (1.5, 0.05). All the curves intersect at (1.0, 0.4). All data are approximate. Graph 3: The vertical axis labeled h of t ranges from 0 to 6 in increments of 2. The K equals 0.5 curve decline rapidly from (0, 6) to (0, 1) and then gradually reaches (1.5, 0.5). The K equals 1 is a horizontal line extending from (0,1) to )1.5, 1). The K equals 2 is a diagonal line with a positive slope extending from (0,0), passing through the points (0.5, 1), (1, 2) and (1.5, 3). The K equals 3 is a concave up, increasing curve starting from (0,0). It passes through the points (0.5, 0.8), (1, 3), (1.5, 6). All data are approximate. Graph 4: The vertical axis labeled H of t ranges from 0 to 3 in increments of 1. The K equals 0.5 curve increases from (0,0) to (1.5,1.4) passing through (1,1). The K equals 1 is a diagonal line with a positive slope increasing from (0,0) to (1.5, 1.5), passing through points (0.5, 0.5), (1, 1). The K equals 2 curve follows a concave up, increasing trend and passes through points (0,0), (1, 1) and (1.5, 2). The K equals 3 curve also follows a concave up, increasing trend and passes through the points (0,0), (1,0) and (1.5, 3). All data are approximate.”
The characteristic life of the Weibull distribution is a special fractile defined by [latex]t_c = 1 / \lambda[/latex]. All Weibull survivor functions pass through the point ([latex]1 / \lambda , \, 1 / e[/latex]), regardless of the value of [latex]\kappa[/latex], as shown in Figure 4.11 for [latex]\lambda = 1[/latex]. Also, since [latex]H(t) = -\ln \, S(t)[/latex], all Weibull cumulative hazard functions pass through the point ([latex]1 / \lambda , \, 1[/latex]), regardless of the value of [latex]\kappa[/latex].
There are several ways to parameterize the Weibull distribution. The previous two paragraphs introduced one such parameterization with a scale parameter λ and a shape parameter [latex]\kappa[/latex]. Another common way to parameterize the Weibull distribution is with the survivor function
where η is a positive scale parameter and β is a positive shape parameter. This is the parameterization used in R. Comparing the two survivor functions, it is clear that the two shape parameters [latex]\kappa[/latex] and β play identical roles, and the two scale parameters λ and η are reciprocals. Both parameterizations correspond to the Weibull distribution, but some careful bookkeeping is necessary to account for the different roles of the various parameters. The version of the Weibull distribution with parameters λ and [latex]\kappa[/latex] will be used consistently throughout this book.
Moments for the Weibull distribution are not as mathematically tractable as those for the exponential distribution. Using the substitution [latex]u = (\lambda t) ^ \kappa[/latex], the rth central moment about the origin is
for [latex]r = 1, \, 2, \, \ldots[/latex]. Using this expression for [latex]E \left[ T^r \right][/latex] with [latex]r = 1[/latex] and [latex]r = 2[/latex] and the shortcut formula for the population variance, the population mean and variance of a Weibull([latex]\lambda, \, \kappa[/latex]) random variable are
and
The associated coefficient of variation is
Using this expression for [latex]E \left[ T^r \right][/latex] with [latex]r = 3[/latex] and [latex]r = 4[/latex] yields the population skewness and kurtosis:
The next example applies the formulas developed thus far for the Weibull distribution to the lifetime of a spring.
Finding fractiles of the Weibull distribution requires only a few steps of algebra. The pth fractile of a Weibull([latex]\lambda, \, \kappa[/latex]) random variable, denoted by tp, can be found by equating the cumulative distribution of T to p and solving for tp:
These fractiles can be useful for establishing warranty periods or setting burn-in periods for manufactured items.
The Weibull distribution has the self-reproducing property. If [latex]T_1, \, T_2, \, \ldots , \, T_n[/latex] are mutually independent component lifetimes having the Weibull distribution with the same shape parameters, then the minimum of these values has the Weibull distribution. More specifically, if [latex]T_i \sim \hbox{Weibull} (\lambda_i, \, \kappa)[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], then [latex]\min {\{ T_1, \, T_2 , \, \ldots, \, T_n \} \sim \hbox{Weibull} \left(\left(\sum_{\,i\,=\,1}^{n} \lambda_i^{\kappa} \right)^{1 / \kappa}, \, \kappa \right)}[/latex].
4.4 Other Lifetime Distributions
Although the exponential and Weibull distributions are popular lifetime models, they are limited in their modeling capability. For example, if it were determined that an item had a bathtub-shaped hazard function, none of these three models would be appropriate unless a piecewise model over time segments of the lifetime were used. Several other models that may be used to describe the distribution of a continuous lifetime T are surveyed in this section.
The distributions for the nonnegative random variable T described here have three types of parameters: location parameters, denoted by a, b, and μ; scale parameters, denoted by λ and σ; and shape parameters, denoted by [latex]\kappa[/latex], γ, and δ. All distributions have support on [latex][0, \, \infty)[/latex] except for the uniform and Pareto distributions.
The one-parameter lifetime models that are summarized in this section are the exponential(λ) and Muth([latex]\kappa[/latex]) distributions. The two-parameter lifetime models summarized here are the Weibull([latex]\lambda, \, \kappa[/latex]), gamma([latex]\lambda, \, \kappa[/latex]), uniform([latex]a, \, b[/latex]), log normal([latex]\mu, \, \sigma[/latex]), log logistic([latex]\lambda, \, \kappa[/latex]), inverse Gaussian([latex]\lambda, \, \mu[/latex]), exponential power([latex]\lambda, \, \kappa[/latex]), Pareto([latex]\lambda, \, \kappa[/latex]), and Gompertz([latex]\delta, \, \kappa[/latex]) distributions. The three-parameter lifetime models summarized here are the Makeham([latex]\delta, \, \kappa, \, \gamma[/latex]), IDB([latex]\delta, \, \kappa, \, \gamma[/latex]), and generalized Pareto([latex]\delta, \, \kappa, \, \gamma[/latex]) distributions. The n-parameter lifetime models summarized here are the hypoexponential([latex]\lambda_1, \, \lambda_2, \, \ldots, \, \lambda_n[/latex]) and hyperexponential([latex]\lambda_1, \, \lambda_2, \, \ldots, \, \lambda_n[/latex]) distributions.
The shapes of the lifetime distribution representations, particularly the hazard function, are useful in determining the appropriate distribution to use to model a lifetime. One-, two-, three-, and n-parameter lifetime distributions are described consecutively in the following paragraphs.
4.4.1 Some One-Parameter Lifetime Models
The one-parameter lifetime distributions defined here have their [latex]f(t)[/latex], [latex]S(t)[/latex], [latex]h(t)[/latex], and [latex]H(t)[/latex] functions given in Table 4.2. The simplest lifetime distribution is the exponential distribution, with a positive scale parameter λ. As indicated in Section 4.2, it is the only continuous distribution with a constant failure rate.
|
Distribution |
[latex]f(t)[/latex] |
[latex]S(t)[/latex] |
[latex]h(t)[/latex] |
[latex]H(t)[/latex] |
Parameters |
|---|---|---|---|---|---|
|
Exponential |
[latex]\lambda e^{-\lambda t}[/latex] |
[latex]e^{-\lambda t}[/latex] |
[latex]\lambda[/latex] |
[latex]\lambda t[/latex] |
[latex]\lambda > 0[/latex] |
|
Muth |
[latex]\left(e^{\kappa \kern 0.04em t} -\kappa \right) e^{\left[-{1 \over \kappa} e^{\kappa \kern 0.04em t} + \kappa \kern 0.04em t + {1 \over \kappa} \right]}[/latex] |
[latex]e^{\left[-{1 \over \kappa} e^{\kappa \kern 0.04em t} + \kappa \kern 0.04em t + {1 \over \kappa} \right]}[/latex] |
[latex]e ^{\kappa \kern 0.04em t} - \kappa[/latex] |
[latex]{1 \over \kappa} e^{\kappa \kern 0.04em t} - \kappa \kern 0.04em t -{1 \over \kappa}[/latex] |
[latex]0 < \kappa \le 1[/latex] |
Muth developed a distribution with a single shape parameter [latex]\kappa[/latex]([latex]0 < \kappa \le 1[/latex]). The Muth distribution is asymptotically equivalent to the unit exponential distribution as [latex]\kappa \to 0[/latex] and has a hazard function that increases from [latex]h(0) = 1 - \kappa[/latex], for all [latex]\kappa[/latex].
4.4.2 Some Two-Parameter Lifetime Models
The two-parameter lifetime distributions defined here have their lifetime distribution representations given in Table 4.3. As outlined in Section 4.3, the Weibull distribution, having positive scale parameter λ and positive shape parameter [latex]\kappa[/latex], is one of the most popular two-parameter lifetime models used in survival analysis. The Weibull distribution includes the exponential distribution as a special case when [latex]\kappa = 1[/latex], and the hazard function increases from zero to infinity when [latex]\kappa > 1[/latex] and decreases from infinity to zero when [latex]\kappa < 1[/latex].
|
Distribution |
[latex]f(t)[/latex] |
[latex]S(t)[/latex] |
[latex]h(t)[/latex] |
[latex]H(t)[/latex] |
Parameters |
|---|---|---|---|---|---|
|
Weibull |
[latex]\displaystyle{\kappa \lambda^{\kappa} t^{\kappa - 1} e^{-(\lambda t)^{\kappa}}}[/latex] |
[latex]\displaystyle{e^{-(\lambda t)^\kappa}}[/latex] |
[latex]\displaystyle{\kappa \lambda^{\kappa} t^{\kappa - 1}}[/latex] |
[latex]\displaystyle{(\lambda t)^{\kappa}}[/latex] |
[latex]\lambda > 0; \ \kappa > 0[/latex] |
|
Gamma |
[latex]\displaystyle{{\lambda(\lambda t) ^ {\kappa - 1} e^{-\lambda t}} \over {\Gamma(\kappa)}}[/latex] |
[latex]\displaystyle{1 - I(\kappa, \, \lambda t)}[/latex] |
[latex]\displaystyle{{\lambda(\lambda t) ^ {\kappa - 1} e ^ {-\lambda t}} \over {\Gamma(\kappa)[1 \kern -0.15em - \kern -0.15em I(\kappa, \, \lambda t)]}}[/latex] |
[latex]\displaystyle{-\ln\left[1 \kern -0.15em - \kern -0.15em I(\kappa, \, \lambda t) \right]}[/latex] |
[latex]\lambda > 0; \ \kappa > 0[/latex] |
|
Uniform |
[latex]\displaystyle{1 \over {b - a}}[/latex] |
[latex]\displaystyle{{b - t} \over {b - a}}[/latex] |
[latex]\displaystyle{1 \over {b - t}}[/latex] |
[latex]\displaystyle{-\ln \left({b - t} \over {b - a} \right)}[/latex] |
[latex]\stackrel{\displaystyle{a \le t \le b;}}{0 \le a < b}[/latex] |
|
Log normal |
[latex]\kern -0.17em \displaystyle{{1 \over {\sigma \kern 0.03em t \sqrt{{2 \pi}}}} \kern 0.02em e^{-{{{(\ln \, t - \mu) ^ 2}} / {2 \sigma ^ 2}}}} \kern -0.17em[/latex] |
[latex]\displaystyle{\int_{t}^{\infty} f(\tau) d \tau}[/latex] |
[latex]\displaystyle{{f(t)} \over {S(t)}}[/latex] |
[latex]\displaystyle{-\ln \, S(t)}[/latex] |
[latex]\stackrel{\displaystyle{-\infty < \mu < \infty;}}{\sigma > 0}[/latex] |
|
Log logistic |
[latex]\displaystyle{{\lambda \kappa (\lambda t) ^ {\kappa - 1}} \over {[1 + (\lambda t) ^ \kappa] ^ 2}}[/latex] |
[latex]\displaystyle{1 \over {1 + (\lambda t) ^ \kappa}}[/latex] |
[latex]\displaystyle{{\lambda \kappa (\lambda t) ^ {\kappa - 1}} \over {1 + (\lambda t) ^ \kappa}}[/latex] |
[latex]\displaystyle{\ln \left[1 + (\lambda t) ^ \kappa \right]}[/latex] |
[latex]\lambda > 0; \ \kappa > 0[/latex] |
|
Inverse Gaussian |
[latex]\sqrt{\lambda \over {2 \pi t ^ 3}} e ^ {{-{{\lambda} (t - \mu)^ 2 / {2 \mu ^ 2 t}}}}[/latex] |
[latex]\displaystyle{\int_{t}^{\infty} f(\tau) d \tau}[/latex] |
[latex]\displaystyle{{f(t)} \over {S(t)}}[/latex] |
[latex]-\ln \, S(t)[/latex] |
[latex]\lambda > 0; \ \mu > 0[/latex] |
|
Exponential Power |
[latex]\lambda \kappa t ^ {\kappa - 1} e ^ {1 - e ^ {\lambda t ^ \kappa} + \lambda t ^ \kappa}[/latex] |
[latex]e ^ {1 - e ^ {\lambda t ^ \kappa}}[/latex] |
[latex]e ^ {\lambda t ^ \kappa} \lambda \kappa t ^ {\kappa - 1}[/latex] |
[latex]e ^ {\lambda t ^ \kappa} - 1[/latex] |
[latex]\lambda > 0; \ \kappa > 0[/latex] |
|
Pareto |
[latex]\displaystyle{{\kappa \lambda ^ \kappa} \over {t ^ {\kappa + 1}}}[/latex] |
[latex]\displaystyle{\left(\lambda \over t \right) ^ {\kappa}}[/latex] |
[latex]\displaystyle{\kappa \over t}[/latex] |
[latex]\displaystyle{\kappa \ln \left(t \over \lambda \right)}[/latex] |
[latex]\stackrel {\displaystyle{t \ge \lambda;}} {\lambda > 0; \ \kappa > 0}[/latex] |
|
Gompertz |
[latex]\displaystyle{\delta \kappa ^ {\kern 0.04em t} e ^ {-\delta (\kappa ^ {\kern 0.04em t} - 1) / \ln \, \kappa}}[/latex] |
[latex]\displaystyle{e ^ {-\delta (\kappa ^ {\kern 0.04em t} - 1) / \ln \, \kappa}}[/latex] |
[latex]\displaystyle{\delta \kappa ^ {\kern 0.04em t}}[/latex] |
[latex]\displaystyle{{\delta \left(\kappa ^ {\kern 0.04em t} - 1 \right)} \over {\ln \, \kappa}}[/latex] |
[latex]\displaystyle{\kappa > 1; \ \delta > 0}[/latex] |
The gamma distribution, has positive scale parameter λ and positive shape parameter [latex]\kappa[/latex]. As with the Weibull distribution, the gamma distribution includes the exponential distribution as a special case when [latex]\kappa = 1[/latex]. The hazard function increases from zero to λ when [latex]\kappa > 1[/latex], decreases from infinity to λ when [latex]\kappa < 1[/latex].
The uniform distribution is a simple two-parameter model. The main application of the uniform distribution in survival analysis is to approximate lifetime distributions over relatively small intervals. The uniform distribution has support on [latex][a, \, b][/latex] with location parameters a and b, where [latex]0 \le a < b[/latex]. The hazard function increases from [latex]h(a) = 1/(b - a)[/latex] to infinity. When [latex]a = 0[/latex] and [latex]b = 1[/latex], the uniform distribution can be used to generate random variates for Monte Carlo simulation by inversion of the cumulative distribution function based on the probability integral transformation.
The log normal distribution has a hazard function shape that places it in the UBT [upside-down bathtub-shaped, or hump-shaped, where [latex]h(t)[/latex] increases initially and then decreases] class. It is parameterized by μ and σ because the logarithm of a log normal random variable is a normal random variable with population mean μ and standard deviation σ. One historical reason that the log normal distribution has been less popular than the Weibull distribution is that its survivor function is not closed form. This is important for estimating parameters for right-censored data sets, although widespread algorithms and computer routines can overcome this issue. The survivor function for a log normal random variable is
where Φ is the cumulative distribution function of a standard normal random variable.
The log logistic distribution has positive scale parameter λ and positive shape parameter [latex]\kappa[/latex]. The hazard function is decreasing when [latex]\kappa \le 1[/latex] and is UBT for [latex]\kappa > 1[/latex]. As with the exponential and Weibull distributions, its survivor function can be inverted in closed form, so log logistic variates can easily be generated by inversion for Monte Carlo simulation. The log logistic distribution is widely used in biomedical applications.
The inverse Gaussian distribution has a positive parameter μ and positive scale parameter λ. Similar to the log normal distribution, the inverse Gaussian distribution is also in the UBT class. The survivor function is not closed form, but can be written in terms of the cumulative distribution function of a standard normal random variable. The population mean of the inverse Gaussian distribution is μ and the population variance is [latex]\mu^{\kern 0.04em 3} / \lambda[/latex], so the parameter μ is not a true location parameter because it does more than just shift the location of the distribution.
The exponential power distribution has a positive scale parameter λ and a positive shape parameter [latex]\kappa[/latex]. The exponential power distribution has two properties that make it unique. First, the hazard function increases exponentially in t, whereas the Weibull hazard function increases in a polynomial fashion. Second, the exponential power distribution is one of the few two-parameter distributions that has a hazard function that can assume a bathtub shape. The hazard function achieves a minimum at [latex]t = [(1 - \kappa) / (\lambda \kappa)]^{1 / \kappa}[/latex] when [latex]\kappa < 1[/latex]. For [latex]\kappa > 1[/latex], the hazard function increases from zero to infinity, and for [latex]\kappa = 1[/latex] the hazard function increases from λ. The distribution has a characteristic life of [latex](1 / \lambda)^{1 / \kappa}[/latex]. The exponential power distribution’s survivor function, which is
can be inverted in closed form, so random variates can easily be generated by inversion.
Pareto devised a probability distribution with support on [latex]t \ge \lambda[/latex] where [latex]\kappa[/latex] is a positive shape parameter and λ is a positive scale parameter. The hazard function for the Pareto distribution decreases to zero from [latex]h(\lambda) = \kappa / \lambda[/latex].
The Gompertz distribution is a lifetime model that has been used to model adult lifetimes in actuarial applications. This distribution has positive shape parameters δ and [latex]\kappa[/latex]. Gompertz assumed that Mill’s ratio, the reciprocal of the hazard function, measures human resistance to death. He assumed this resistance decreases over time at a rate proportional to itself; that is,
where [latex]\kappa[/latex] is a constant. The solution to this separable differential equation is [latex]h(t) = \delta e^{\kern 0.04em ct}[/latex], where [latex]e^{\kern 0.04em c} = \kappa[/latex]. The hazard function increases from [latex]h(0) = \delta[/latex].
4.4.3 Some Three-Parameter Lifetime Models
The three-parameter lifetime distributions defined here have their [latex]f(t)[/latex], [latex]S(t)[/latex], [latex]h(t)[/latex], and [latex]H(t)[/latex] functions given in Table 4.4. The Makeham distribution has three positive shape parameters and is a generalization of the Gompertz distribution with γ included in the hazard function. Whereas the Gompertz distribution has been used to model lifetimes in terms of death from natural causes, the Makeham distribution takes into account the possibility of accidental deaths by including the extra parameter. The hazard function increases from [latex]\delta + \gamma[/latex].
|
Distribution |
[latex]f(t)[/latex] |
[latex]S(t)[/latex] |
[latex]h(t)[/latex] |
[latex]H(t)[/latex] |
Parameters |
|---|---|---|---|---|---|
|
Makeham |
[latex]\displaystyle{(\gamma + \delta \kappa ^ {\kern 0.06em t}) e ^ {-\gamma \kern 0.05em t - {\delta (\kappa ^ {\kern 0.05em t} - 1) / {\ln \, \kappa}}}}[/latex] |
[latex]\displaystyle{e ^ {-\gamma \kern 0.05em t - {{\delta (\kappa ^ {\kern 0.06em t} - 1)} / {\ln \, \kappa}}}}[/latex] |
[latex]\displaystyle{\gamma + \delta \kappa ^ {\kern 0.06em t}}[/latex] |
[latex]\displaystyle{\gamma \kern 0.05em t + {{\delta (\kappa ^ {\kern 0.06em t} - 1)} \over {\ln \, \kappa}}}[/latex] |
[latex]\stackrel{\displaystyle \delta \ge 0; \ \kappa > 1;}{\gamma > 0}[/latex] |
|
IDB |
[latex]\displaystyle{{{(1 + \kappa \kern 0.04em t) \delta \kern 0.02em t + \gamma} \over {(1 + \kappa \kern 0.04em t) ^ {\gamma / \kappa + 1}}} e ^ {- \delta \kern 0.03em t ^ 2 / 2}}[/latex] |
[latex]\displaystyle{(1 \kern -0.15em + \kern -0.15em \kappa \kern 0.04em t) ^ {-\gamma / \kappa} e ^ {- \delta \kern 0.03em t ^ 2 / 2}}[/latex] |
[latex]\displaystyle{\delta \kern 0.02em t \kern -0.15em + \kern -0.15em {\gamma \over {1 \kern -0.15em + \kern -0.15em \kappa \kern 0.04em t}}}[/latex] |
[latex]\displaystyle{{\delta \over 2} t ^ 2 \kern -0.15em + \kern -0.15em {\gamma \over \kappa} \ln(1 \kern -0.15em + \kern -0.15em \kappa \kern 0.04em t)}[/latex] |
[latex]\stackrel{\displaystyle \delta \ge 0; \ \kappa \ge 0;}{\gamma \ge 0}[/latex] |
|
Generalized Pareto |
[latex]\displaystyle{\left(\gamma \kern -0.10em + \kern -0.10em {\kappa \over {t + \delta}} \right) \left(1 \kern -0.15em + \kern -0.15em {t \over \delta} \right) ^ {-\kappa} e ^ {- \gamma \kern 0.05em t}}[/latex] |
[latex]\displaystyle{\left (1 + {t \over \delta} \right) ^ {- \kappa} e ^ {- \gamma \kern 0.05em t}}[/latex] |
[latex]\displaystyle{\gamma + {\kappa \over {t + \delta}}}[/latex] |
[latex]\displaystyle{\gamma \kern 0.05em t \kern -0.15em + \kern -0.15em \kappa \ln \left(1 \kern -0.15em + \kern -0.15em {t \over \delta} \right)}[/latex] |
[latex]\stackrel{\displaystyle \delta > 0; \ \gamma \ge 0;}{\kappa \ge - \delta \gamma}[/latex] |
The IDB (increasing, decreasing, bathtub) distribution is a three-parameter model with a hazard function that can exhibit increasing ([latex]\delta \ge \gamma \kappa[/latex]), decreasing ([latex]\delta = 0[/latex]), and bathtub shapes ([latex]0 < \delta < \gamma \kappa[/latex]). The distribution has shape parameters [latex]\delta \ge 0[/latex], [latex]\kappa \ge 0[/latex], and [latex]\gamma \ge 0[/latex]. Special cases of the IDB distribution are the Rayleigh distribution when [latex]\gamma = 0[/latex] and the exponential distribution when [latex]\delta = \kappa = 0[/latex] and [latex]\gamma > 0[/latex].
The generalized Pareto distribution is another three-parameter distribution with shape parameters [latex]\delta, \kappa,[/latex] and [latex]\gamma[/latex]. It is able to achieve an increasing hazard function when [latex]\kappa < 0[/latex], a decreasing hazard function when [latex]\kappa > 0[/latex], and a constant hazard function when [latex]\kappa = 0[/latex]. For all parameter values, [latex]h(0) = \gamma \,+\, \kappa / \delta[/latex] and [latex]\lim_{\, t \,\to\, \infty } h(t) = \gamma[/latex]. The special cases of [latex]\gamma = 0[/latex] and [latex]\kappa = - \delta \gamma[/latex] result in the hazard functions
for [latex]t \ge 0[/latex].
4.4.4 Some n-Parameter Lifetime Models
Two n-parameter distributions are related to the exponential distribution. The first is the hypoexponential distribution. If [latex]T_i \sim[/latex] exponential([latex]\lambda_i[/latex]) for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], then [latex]{T = T_1 + T_2 + \cdots + T_n}[/latex] has the hypoexponential distribution. The hypoexponential distribution collapses to the Erlang distribution with parameters λ and n when [latex]\lambda = \lambda_1 = \lambda_2 = \cdots = \lambda_n[/latex]. The hypoexponential distribution is in the IFR class for all values of its parameters.
A second n-parameter distribution is the hyperexponential distribution. If [latex]T_i \sim[/latex] exponential([latex]\lambda_i[/latex]) for [latex]i = 1, \, 2, \, \ldots, \, n[/latex] and T has probability density function
where [latex]p_1 + p_2 + \cdots + p_n = 1[/latex] and [latex]p_i > 0[/latex] for [latex]i = 1, \, 2, \, \ldots , \, n[/latex], then T has the hyperexponential distribution. This lifetime distribution is a mixture of exponential distributions. The hyperexponential distribution collapses to the exponential distribution with failure rate λ when [latex]\lambda = \lambda_1 = \lambda_2 = \cdots = \lambda_n[/latex]. The hyperexponential distribution is in the DFR class for all values of its parameters.
4.4.5 Summary
Figure 4.13 shows how these univariate lifetime distributions are related to one another. Each oval represents one lifetime distribution, listing its name, parameter(s), and support. Solid arrows connecting the distributions denote special cases and transformations. An example of a special case is the arrow pointing from the Weibull distribution to the exponential distribution with the label [latex]\kappa = 1[/latex]. An example of a transformation is the arrow pointing from the exponential distribution to the chi-square distribution with the label [latex]2 \lambda \sum_{i\,=\,1}^n T_i[/latex] (iid). This result is given in Theorem 4.5. Another example of a transformation is the self-loop on the exponential distribution, where the minimum of independent exponential random variables is also exponential. This result is given in Theorem 4.4. Dashed arrows denote limiting distributions, which typically arise as one of the parameters approaches 0 or infinity. An example of a limiting distribution is the arrow pointing from the gamma distribution to the normal distribution with the label [latex]\kappa \rightarrow \infty[/latex]. The limiting distribution of a gamma random variable converges to the normal distribution as its shape parameter increases.
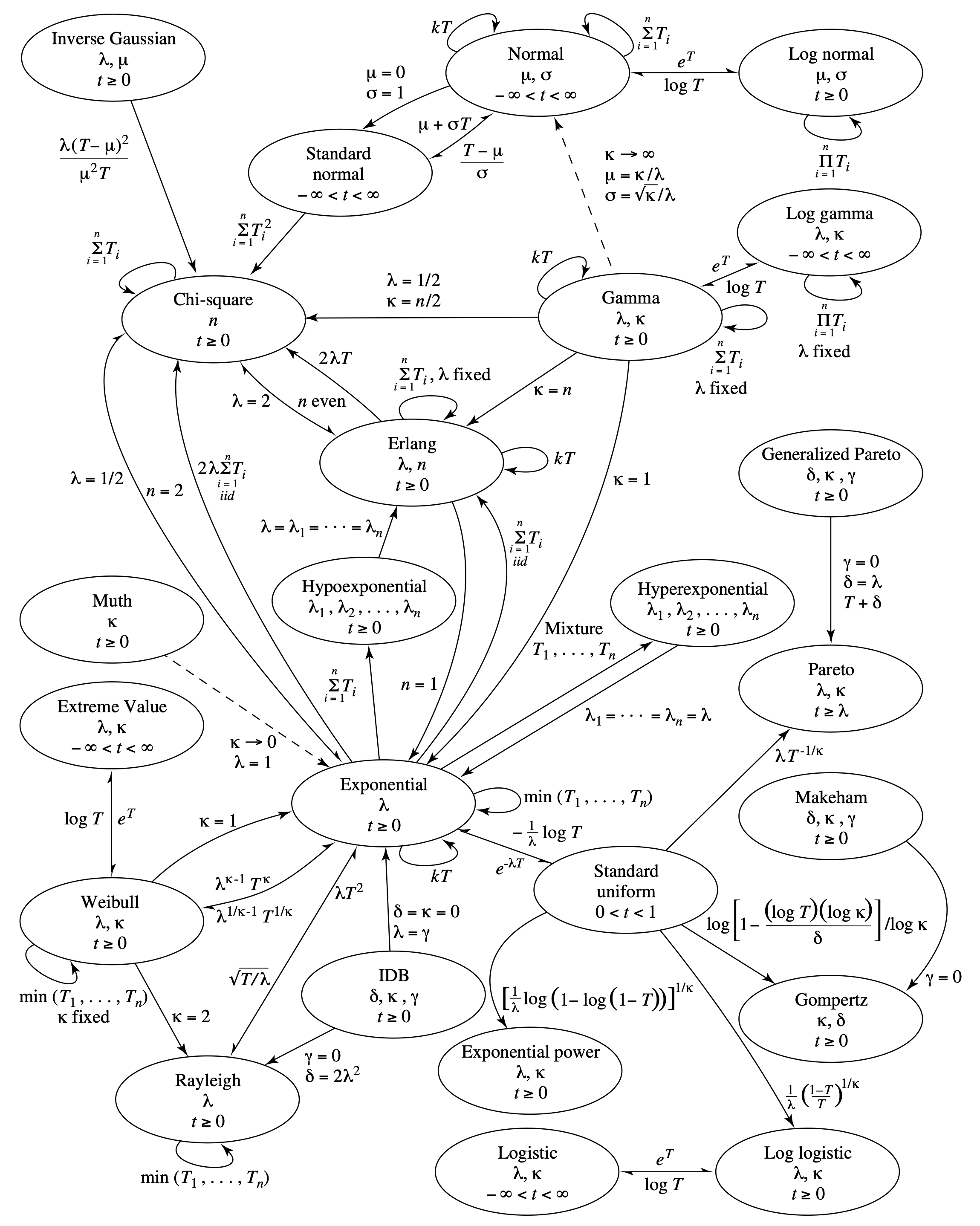
Long Description for Figure 4.13
Each distribution is represented by an oval. Solid arrows connecting the distributions indicate special cases and transformations. Dashed arrows represent the limiting distribution. Some of the distributions are as follows. A solid arrow pointing from Weibull distribution to exponential is labeled k equals 1. A solid arrow pointing from standard uniform to exponential is e to the power of negative lambda T. The self loop transformation is exponential with the minimum of T 1 to T n, and k T. A solid arrow from I D B to exponential distribution is delta equals k equals 0, and lambda equals gamma. A solid arrow from I D B to Rayleigh is labeled gamma equals 0 and delta equals 2 lambda squared. A dashed arrow from Muth to Exponential represents k tending to 0 as lambda equals 1. A dashed arrow from Gamma to Normal distribution represents k tends to infinity as mu equals k over lambda and sigma equals the square root of k over lambda. Solid arrows connecting other distributions are as follows. Inverse Gaussian and Chi square, Standard normal and chi square, normal and standard normal, Log normal and normal, Gamma and Chi square, Gamma and log gamma, Erlang and chi square, Erlang and Gamma, hypo exponential and Erlang, Exponential and hypo exponential, Exponential and hyper exponential, Standard uniform and exponential, Standard uniform and exponential power, logistic and log logistic, Standard uniform and Gompertz, Standard uniform and Log logistic, Standard uniform and Pareto, Generalized Paretto and Paretto etcetera. The self loop distributions are gamma, exponential, Weibull, Rayleigh, chi square, Normal, and log gamma functions.
Table 4.5 contains a summary of the distribution classes to which the distributions belong. Double lines are used to separate the distributions by the number of parameters. For each class to which a distribution belongs, the corresponding set of parameter values is specified. The distribution classes that are considered are IFR, DFR, BT, and UBT.
|
Distribution |
IFR |
DFR |
BT |
UBT |
|---|---|---|---|---|
|
Exponential |
[latex]{\rm YES}_{\rm \, all \ \lambda}[/latex] |
[latex]{\rm YES}_{\rm \, all \ \lambda}[/latex] |
NO |
NO |
|
Muth |
[latex]{\rm YES}_{\rm \, all \ \kappa}[/latex] |
NO |
NO |
NO |
|
Weibull |
[latex]{\rm YES}_{\, \kappa \ge 1}[/latex] |
[latex]{\rm YES}_{\, \kappa \le 1}[/latex] |
NO |
NO |
|
Gamma |
[latex]{\rm YES}_{\, \kappa \ge 1}[/latex] |
[latex]{\rm YES}_{\, \kappa \le 1}[/latex] |
NO |
NO |
|
Uniform |
[latex]{\rm YES}_{{\rm \, all} \ a \ {\rm and} \ b}[/latex] |
NO |
NO |
NO |
|
Log normal |
NO |
NO |
NO |
[latex]{\rm YES}_{\rm \, all \ \mu \ and \ \sigma}[/latex] |
|
Log logistic |
NO |
[latex]{\rm YES}_{\, \kappa \le 1}[/latex] |
NO |
[latex]{\rm YES}_{\, \kappa > 1}[/latex] |
|
Inverse Gaussian |
NO |
NO |
NO |
[latex]{\rm YES}_{\rm \, all \ \lambda \ and \ \mu}[/latex] |
|
Exponential Power |
[latex]{\rm YES}_{\, \kappa \ge 1}[/latex] |
NO |
[latex]{\rm YES}_{\, \kappa < 1}[/latex] |
NO |
|
Pareto |
NO |
[latex]{\rm YES}_{\rm \, all \ \kappa}[/latex] |
NO |
NO |
|
Gompertz |
[latex]{\rm YES}_{\rm \, all \ \delta\ and \ \kappa}[/latex] |
NO |
NO |
NO |
|
Makeham |
[latex]{\rm YES}_{\rm \, all \ \delta\ and \ \kappa}[/latex] |
NO |
NO |
NO |
|
IDB |
[latex]{\rm YES}_{\, \delta \ge \gamma \kappa}[/latex] |
[latex]{\rm YES}_{\, \delta = 0}[/latex] |
[latex]{\rm YES}_{\, 0 < \delta < \gamma \kappa}[/latex] |
NO |
|
Generalized Pareto |
[latex]{\rm YES}_{\, \kappa \le 0}[/latex] |
[latex]{\rm YES}_{\, \kappa \ge 0}[/latex] |
NO |
NO |
|
Hypoexponential |
[latex]{\rm YES}_{\rm \, all \ \lambda_1, \, \lambda_2, \ldots , \, \lambda_n}[/latex] |
[latex]{\rm YES}_{\, n = 1}[/latex] |
NO |
NO |
|
Hyperexponential |
[latex]{\rm YES}_{\, \lambda_1 = \lambda_2 = \cdots = \lambda_n}[/latex] |
[latex]{\rm YES}_{\rm \, all \ \lambda_1, \, \lambda_2, \ldots , \, \lambda_n}[/latex] |
NO |
NO |
4.5 Moment Ratio Diagrams
The lifetime distributions introduced in this chapter have been presented in a serial fashion without much attention being directed toward looking at all of them simultaneously. Isolating their presentation in this fashion is unfortunate; it would be of benefit to view all of these distributions simultaneously. One way to view these probability distributions simultaneously is to place them on a graph of their moments. These graphs are often known as moment-ratio diagrams. A moment-ratio diagram is the locus of pairs of standardized moments for a particular probability distribution plotted on a single set of axes. Moment-ratio diagrams are useful for (1) quantifying the “distance” or “proximity” between univariate probability distributions based on their second, third, and fourth moments, (2) illustrating the limiting behavior of probability distributions, (3) highlighting the versatility of a particular probability distribution based on the range of values that the moments can assume, and (4) generating a list of potential probability models based on a data set.
4.5.1 Skewness vs. Coefficient of Variation
As one illustration of a moment-ratio diagram, Figure 4.14 contains a plot of the population skewness
on the vertical axis, versus the population coefficient of variation
on the horizontal axis for several of the lifetime distributions introduced in this chapter, where μ and σ are the population mean and standard deviation of the random variable T. Some features of this moment-ratio diagram are listed below.
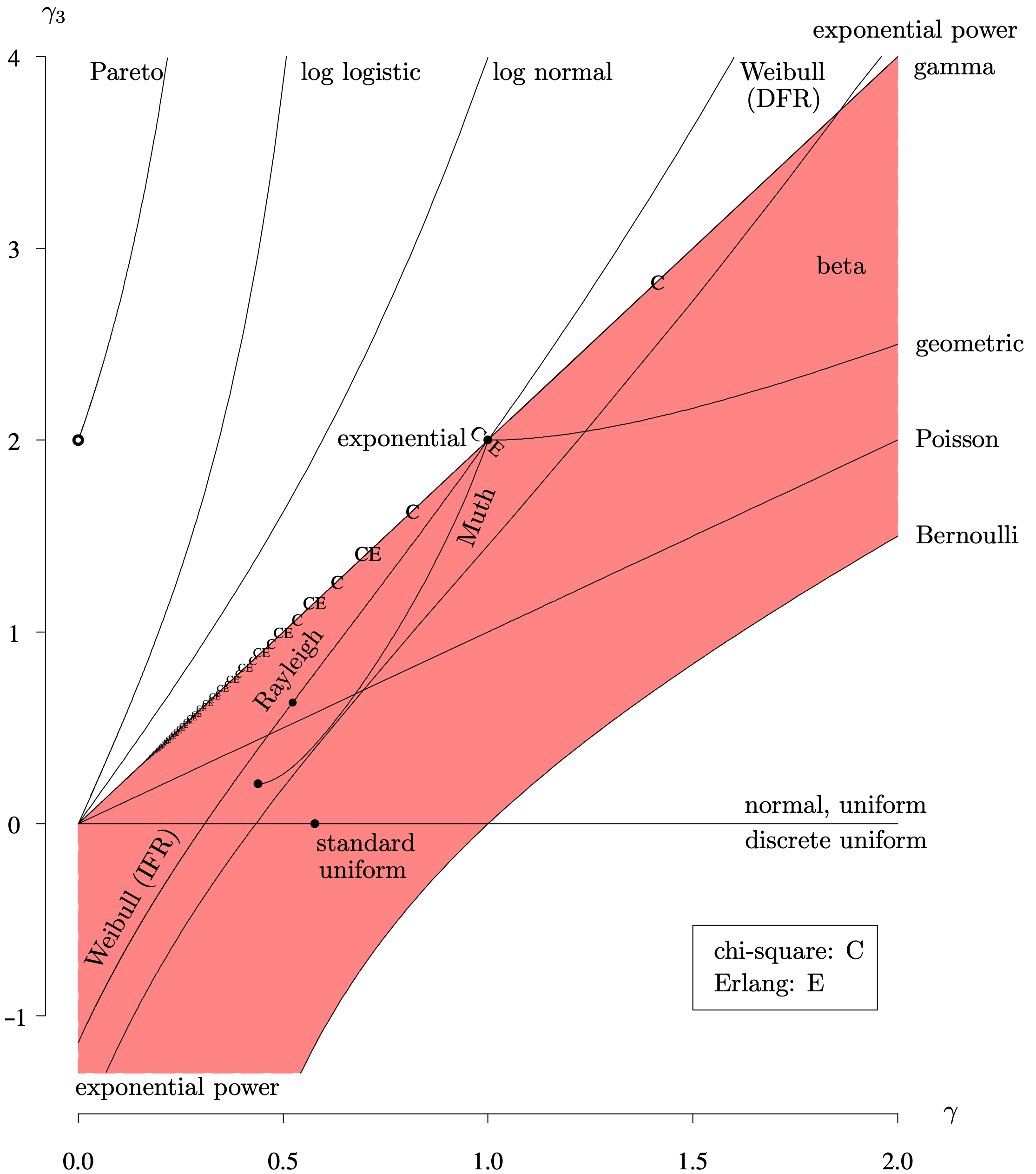
Long Description for Figure 4.14
The horizontal axis measures the population coefficient of variation and ranges from 0.0 to 2.0 in increments of 0.5 units. The vertical axis measures the skewness of gamma 3 and ranges from negative 1 to 4. A horizontal line is drawn at a gamma 3 value of 0 representing standard normal distribution. Above the horizontal line is a normal and uniform distribution. Below the horizontal line is the discrete uniform distribution. Poisson distribution is drawn as a line from (0, 0) to (2.0, 2). The overlapping gamma and Weibull D F R distributions are drawn from (0, 0) to (2.0, 4). Log normal curves concave upward from (0, 0) to (1.0, 4). Log logistic curves concave upward from (0, 0) to (0.5, 4). The Pareto function begins with an open dot at (0.0, 2), and curves concave up to (0.2, 4). Muth distribution begins with a solid dot at (0.4, 0.2), increases in a concave up manner, intersects the gamma distribution at (1.0, 2), and from there the geometric distribution increases to (2.0, 2.4). The Weibull I F R distribution increases from (0.0, negative 1) to (1.0, 2) with the Rayleigh function plotted at (0.5, 0.7). The Chi square C and Erlang E functions are plotted along the gamma function. Bernoulli function increases in a concave down manner from (0.5, negative 1) to (2.0, 1.5). The exponential distribution increases from (0.2, negative 1) to (2.0, 4). The region between gamma function and Bernoulli function is shaded. All data are estimated.
- The locus of points associated with the various probability distribution consist of either a single point (for example, the Rayleigh distribution), a curve (for example, the log logistic distribution), or a region (for example, the beta distribution).
- There are two gathering points: the exponential distribution at [latex]\left( \gamma , \, \gamma_3 \right) = (1, \, 2)[/latex] and a degenerate distribution at [latex]\left( \gamma , \, \gamma_3 \right) = (0, \, 0)[/latex].
- The Poisson distribution, with [latex]\gamma_3 = \gamma[/latex], and the gamma distribution, with [latex]\gamma_3 = 2 \gamma[/latex], have linear relationships between γ and γ3.
- The limiting values of the beta distribution region are the line associated with the gamma distribution [latex]\gamma_3 = 2 \gamma[/latex] and the curve associated with the Bernoulli distribution [latex]\gamma_3 = \gamma - 1 / \gamma[/latex].
- Symmetric distributions, such as the [latex]N\left( \mu, \, \sigma ^ {\, 2} \right)[/latex], [latex]U(a, \, b)[/latex], and discrete uniform distributions, all have population skewness [latex]\gamma_3 = 0[/latex].
- The curves associated with the gamma and Weibull distributions intersect at the exponential distribution, which is associated with shape parameter [latex]\kappa = 1[/latex].
- The open point associated with the Pareto distribution gives the limiting distribution as [latex]\kappa \rightarrow \infty[/latex]. The values of γ and γ3 are defined for [latex]\kappa > 3[/latex].
- The chi-square distribution, indicated by a C for various values of its degrees of freedom, and the Erlang distribution, indicated by an E for various values of its integer shape parameter, coincide when the degrees of freedom for the chi-square distribution are even. This accounts for the alternating pattern of C and CE labels along the line for the gamma distribution.
4.5.2 Kurtosis vs. Skewness
A second moment-ratio diagram, which is given in Figure 4.15 is a plot of the population kurtosis
on the vertical axis, versus the population skewness
on the horizontal axis for several lifetime distributions introduced in this chapter. (Some authors prefer to work with the excess population kurtosis [latex]\gamma_4 - 3[/latex].) Although it uses higher-order moments, it is considered the more classic moment-ratio diagram because the distributions plotted consist of points, curves, and regions that are independent of location and scale parameters. The population skewness scale can sometimes be replaced by the squared skewness, resulting in what is known as a Cullen and Frey graph. Figure 4.15 contains a moment-ratio diagram for the population skewness versus the population kurtosis, plotted upside down per tradition.
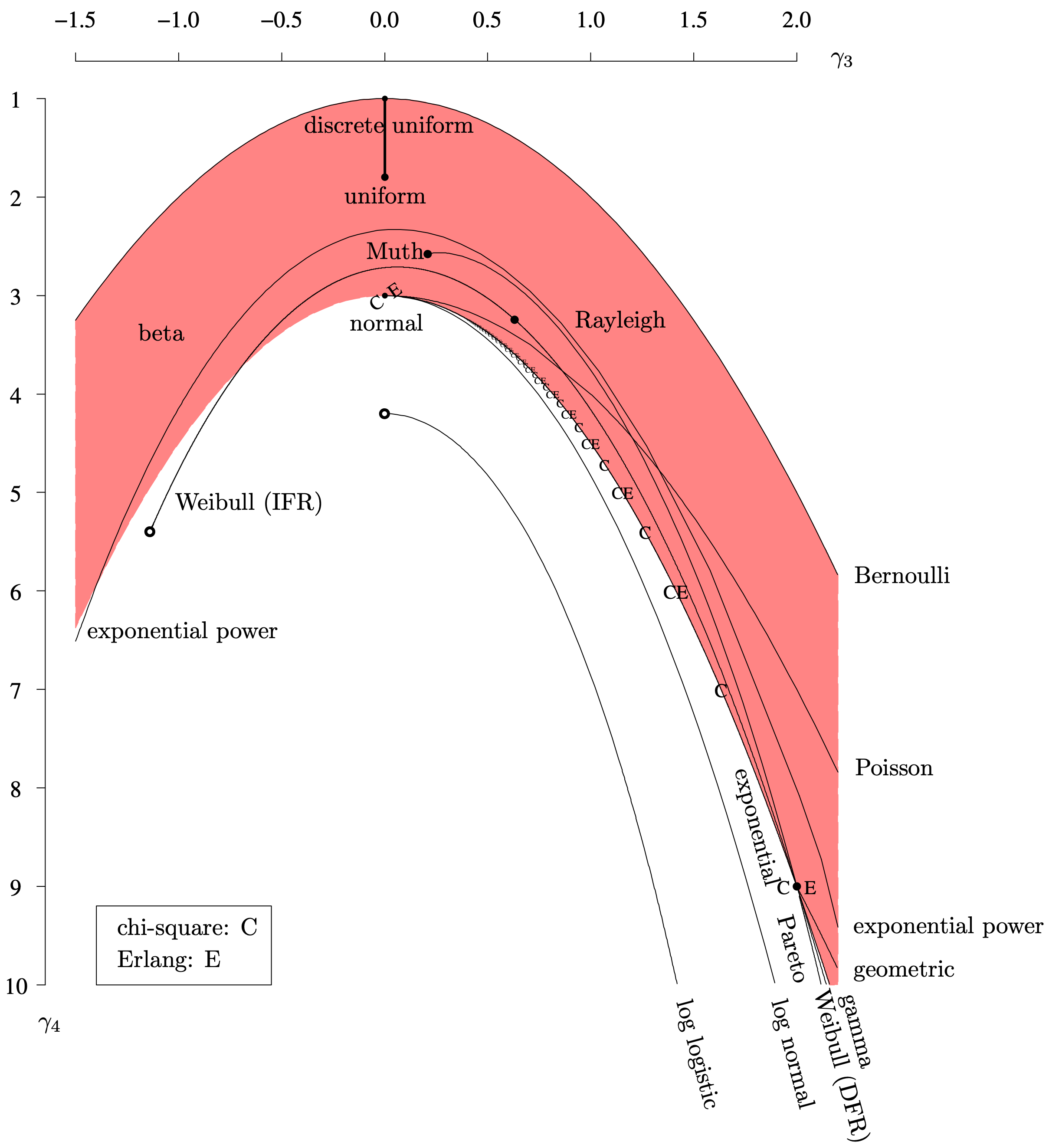
Long Description for Figure 4.15
The horizontal axis measures the population skewness gamma 3 and ranges from negative 1.5 to 2.0 in increments of 0.5 units. The vertical axis measures the population kurtosis gamma 4 and ranges from 1 to 10 from top to bottom. All distributions are plotted upside down in a concave down manner. The discrete function and Bernoulli begins at (negative 1.5, 3), peak at (0.0, 1), and ends at (2.0, negative 6). The Muth function starts at (negative 1.5, 6.5), peaks at (0.0, 2.5), and ends at (2.0, 5.5). The Weibull I F R Function begins with an open dot at (negative 1.0, 5.5), peaks at (0.0, 3), and then decreases. The exponential power and geometric, Poisson distributions, Pareto distribution, and Weibull D F R all are plotted in a concave down manner with a peak at 0.0. The log logistic curve begins with an open dot at (0.0, 4.5), and increases to (1.5, 10). The Chi-square C distribution and Erlang distribution E are plotted. The region between the discrete uniform function and the normal function are shaded, and they include the beta function, Rayleigh function, and Muth function. All data are estimated.
The locus of [latex]\left( \gamma_3 , \, \gamma_4 \right)[/latex] values that a distribution occupies in Figure 4.15 typically depends on the number of shape parameters. The Rayleigh(λ) distribution, for example, with just a scale parameter, occupies just the single point because it has no shape parameters. The gamma distribution, on the other hand, occupies the curve [latex]\gamma_3 = 3 \gamma_2 ^ {\kern 0.08em 2} + 3[/latex] because it has one shape parameter. Finally, the beta distribution occupies a region because it has two shape parameters. Some further features of this moment-ratio diagram are listed below.
-
- There are two gathering points: the exponential distribution at [latex]\left( \gamma_3 , \, \gamma_4 \right) = (2, \, 9)[/latex] and the normal distribution at [latex]\left( \gamma_3 , \, \gamma_4 \right) = (0, \, 3)[/latex]. This is further evidence of the centrality of these two distributions in probability theory: the exponential distribution plays a pivotal role in stochastic processes (for example, queueing theory and survival analysis) and the normal distribution plays a pivotal role in classical statistics. Stochastic processes can be thought of as probability over time; statistics can be thought of as probability applied to data.
- Once again, the beta distribution covers the largest amount of territory in Figure 4.15, highlighting its versatility as a probability model.
- The smallest possible value of the population kurtosis is [latex]\gamma_4 = 1[/latex], which is achieved by the Bernoulli distribution with [latex]p = 1 / 2[/latex]. This distribution is equivalent to the discrete uniform distribution with parameters 0 and 1.
- The curves associated with the gamma and Weibull distributions again intersect at the exponential distribution at [latex]\left( \gamma_3 , \, \gamma_4 \right) = (2, \, 9)[/latex], which corresponds to the shape parameter [latex]\kappa = 1[/latex].
-
- The discrete uniform distribution is plotted as a solid line between its limits as a two-mass value at [latex]\left(\gamma_3, \, \gamma_4 \right) = (0, \, 1)[/latex] and its limiting distribution (as the number of mass values increases) at [latex]\left(\gamma_3, \, \gamma_4 \right) = (0, \, 1.8)[/latex]. The locus of points is actually a series of points along this line.
A statistician can plot the sample skewness and the sample kurtosis
for a set of data values [latex]T_1, \, T_2, \, \ldots, \, T_n[/latex], sample mean [latex]\bar T[/latex], and sample standard deviation S on Figure 4.15 for a particular data set. Doing so gives a sense for which of the distributions might be candidate probability models for the implied population distribution. The moment-ratio diagram allows a statistician to compare several candidate distributions simultaneously in terms of their moments.
4.6 Proportional Hazards Model
The proportional hazards model is appropriate for including a vector of covariates (for example, the turning speed and feed rate for a drill bit) in a lifetime model. It is often known as the Cox proportional hazards model because it was devised by British statistician Sir David Cox in 1972. A covariate—often called an explanatory variable—is a variable that influences the survival time of the item under consideration. Covariates might account for the fact that the population is not truly homogeneous, or they might account for treatments imposed on the population.
The [latex]q \times 1[/latex] vector [latex]{\boldsymbol z = (z_1, \, z_2, \, \ldots, \, z_q) ^ \prime}[/latex] contains q covariates associated with a particular item. These covariates might be treatments, stresses, intrinsic properties of items, or exogenous (environmental) variables. The simplest case is the two-population situation modeled by a single ([latex]q = 1[/latex]) binary covariate z, where [latex]z = 0[/latex] typically corresponds to the control group and [latex]z = 1[/latex] typically corresponds to the treatment group. A second, slightly more complicated example arises when a single covariate assumes a continuous value (for example, dosage in a medical setting or turning speed in a manufacturing setting). The objective in an analysis of this type might be to find the dosage or turning speed that minimizes risks or costs, respectively. Other possibilities for the elements of [latex]{\boldsymbol z}[/latex] include cumulative load applied, time-varying stresses, and environmental factors.
The covariates increase or decrease the hazard function in the proportional hazards model. This model was originally developed for medical settings in which covariates are usually patient characteristics such as age, gender, cholesterol level, or blood pressure. The models are often used to determine which covariate has the most significant impact on survival or to compare the survival patterns for different treatments (for example, chemotherapy versus surgery for cancer) by factoring out the impact of the covariates.
One issue of immediate interest is how to link the covariates to a lifetime distribution. One approach is to define one lifetime model when [latex]{\boldsymbol z} = {\bf 0}[/latex] (often called the baseline distribution) and other models when [latex]{\boldsymbol z} \not= {\bf 0}[/latex]. One problem that arises with this approach is that there might be dozens or even thousands of possible values associated with [latex]{\boldsymbol z} \not= {\bf 0}[/latex], and a separate lifetime model would need to be defined for each of these vectors. The more practical approach is to define a single lifetime model which is appropriate for all values of [latex]{\boldsymbol z}[/latex] in order to simplify the modeling.
The baseline distribution corresponds to having all the covariates equal to zero. In a reliability setting, this is typically the normal operating conditions for the item. Other covariate vectors are often used for accelerated environmental conditions. In a biomedical setting, the baseline is typically the control group that receives either no treatment or the standard treatment for a particular disease. The covariates are linked to the lifetime by the link function [latex]\psi ({\boldsymbol z})[/latex], which typically satisfies [latex]\psi({\boldsymbol 0}) = 1[/latex] and [latex]\psi ({\boldsymbol z}) > 0[/latex] for all [latex]{\boldsymbol z}[/latex]. When a link function satisfies these conditions, then [latex]{\boldsymbol z = }{\bf 0}[/latex] implies that [latex]S_0 (t) \equiv S(t)[/latex]. The most general case is to let [latex]\psi ({\boldsymbol z})[/latex] be any function of the covariates.
The covariates increase the hazard function when [latex]\psi ({\boldsymbol z}) > 1[/latex] or decrease the hazard function when [latex]\psi ({\boldsymbol z}) < 1[/latex]. A popular choice is the log-linear link function [latex]\psi ({\boldsymbol z}) = e^{\kern 0.09em {\boldsymbol \beta}^ \prime {\boldsymbol z}}[/latex], where [latex]{\boldsymbol \beta} = (\beta_1, \, \beta_2, \, \ldots, \, \beta_q) ^ \prime[/latex] is a [latex]q \times 1[/latex] vector of regression coefficients corresponding to the q covariates. The log-linear link function satisfies [latex]\psi ({\boldsymbol z}) > 0[/latex] for all vectors [latex]{\boldsymbol z}[/latex] and [latex]{\boldsymbol \beta}[/latex]. Other, less popular choices for the link function are [latex]\psi ({\boldsymbol z}) = {\boldsymbol \beta} ^ {\kern 0.00em \prime} {\boldsymbol z}[/latex] and [latex]\psi ({\boldsymbol z}) = ({\boldsymbol \beta} ^ {\kern 0.00em \prime} {\boldsymbol z})^{-1}[/latex]. Both alternative choices suffer from the limitation that [latex]{\psi ({\boldsymbol z}) < 0}[/latex] for some values of [latex]{\boldsymbol \beta}[/latex] and [latex]{\boldsymbol z}[/latex], resulting in a constrained optimization problem when the models are fitted to data. The left-hand side of this model is often written as [latex]h(t; \, {\boldsymbol z})[/latex] because survival is now a function of both time and the covariate vector [latex]{\boldsymbol z}[/latex].
Regression modeling tools, such as indicator variables, modeling of interaction terms, modeling of nonlinear relationships between variables, and stepwise selection of significant covariates, can all be used here in the same fashion as in regression modeling covered earlier in the text. Estimation of the regression coefficients [latex]\beta_1, \, \beta_2, \, \ldots, \, \beta_q[/latex] and the baseline distribution parameters from a data set consisting of times to failure and associated covariates is introduced in the next chapter. The proportional hazards model has a unique feature that allows estimation of the regression parameters (the [latex]{\boldsymbol \beta}[/latex] vector) without knowledge of the baseline distribution.
Reliability engineers often use accelerated conditions to induce failures. These conditions include voltage, current, pressure, impact, and humidity. The results from the fitted proportional hazards model can then be extrapolated back to the standard operating conditions by adjusting the values of the covariates. The accelerated levels of the covariates must be chosen carefully based on sound engineering judgment and previous experience in order to assure that failure modes that would not occur in the standard operating conditions are not induced by the accelerated testing environment.
The other lifetime distribution representations can be determined for the proportional hazards model. For example, the cumulative hazard function for a random variable T with covariates [latex]{\boldsymbol z}[/latex] is
Similarly,
Finally,
The notation has been simplified in the three expressions above; these functions are more accurately expressed as [latex]H(t, \, {\boldsymbol z} )[/latex], [latex]S(t, \, {\boldsymbol z} )[/latex], and [latex]f(t, \, {\boldsymbol z} )[/latex]. Table 4.6 summarizes the various lifetime distribution representations for the proportional hazards models. This table allows a modeler to determine any of the four lifetime distribution representations for either model once the baseline distribution and link function are specified, as illustrated in the next example.
|
Representation |
Proportional Hazards |
|---|---|
|
[latex]S(t)[/latex] |
[latex]\big[S_0 (t)\big]^{\psi ({\boldsymbol z})}[/latex] |
|
[latex]f(t)[/latex] |
[latex]f_0 (t) \psi ({\boldsymbol z}) \big[S_0 (t)\big] ^ {\psi ({\boldsymbol z}) - 1}[/latex] |
|
[latex]h(t)[/latex] |
[latex]\psi ({\boldsymbol z}) h_0 (t)[/latex] |
|
[latex]H(t)[/latex] |
[latex]\psi ({\boldsymbol z}) H_0 (t)[/latex] |
This chapter has contained a brief introduction to probability models for univariate lifetime distributions, both without and with associated covariates. These models are appropriate for a nonnegative random variable T with applications in reliability, biostatistics, actuarial science, economics, sociology, etc. The distribution of T can be defined by one of five lifetime distribution representations: the survivor function, the probability density function, the hazard function, or the cumulative hazard function. The exponential distribution is a key central lifetime distribution because it is the only continuous distribution having both a constant hazard function and the memoryless property. The Weibull distribution is a two-parameter lifetime distribution that includes the exponential distribution as a special case when its shape parameter [latex]\kappa[/latex] is equal to 1. The Cox proportional hazards model provides one way to incorporate a vector of covariates [latex]{\boldsymbol z}[/latex] into a lifetime model. This model contains a link function [latex]\psi({\boldsymbol z})[/latex] which links the values of the covariates to the failure time distribution. The next chapter introduces statistical methods that can be applied to lifetime data.
4.7 Exercises
-
4.1 Let [latex]t^{\ast} > 0[/latex] be the mode value for a continuous lifetime T. Show that [latex]h ^ {\kern 0.04em \prime}( t^{\ast} ) = [h( t^{\ast} )]^2[/latex].
-
4.2 The probability that an item will survive a 1000-hour mission is 0.4. If the item is operating 800 hours into the mission, the probability of surviving the remaining 200 hours of the mission is 0.85. What is the probability that the item survives the initial 800 hours of the mission?
-
4.3 The hazard function shown below is for a continuous random variable measured in hours.
- Find [latex]S(4)[/latex].
- Find [latex]S(10)[/latex].
- Find [latex]f(10)[/latex].
-
4.4 Draw the survivor function corresponding to the probability density function illustrated below. Use a straight edge whenever the function is linear. The rectangles and triangle on the probability density function all have area [latex]1 / 3[/latex].
Long Description for Unnumbered Figure 1
The horizontal axis t ranges from 0 to 12 in increments of 1 unit. The vertical axis f of t ranges from 0.0 to 0.3 in increments of 0.1 units. The pattern of the function is as follows. A solid horizontal line runs from (0, 0.0) to (3, 0.0), a dashed vertical line rises from (3, 0.0) to (3, 0.1), a solid horizontal line runs from (3, 0.12) to (6, 0.12), and a dashed vertical line runs from (6, 0.12) to (6, 0.0). There is a solid horizontal line from (6, 0.0) to (8, 0.0), a dashed vertical line from (8, 0.0) to (8, 0.35), a diagonal line from (8, 0.35) to (8, 0.0), a solid horizontal line from (10, 0.0) to (11 0.0), a dashed vertical line from (11, 0.0) to (11, 0.35), a solid horizontal line from (11, 0.35) to (12, 0.35), and a dashed vertical line from (12, 0.35) to (12, 0.0). All data are estimated.
-
4.5 Consider the hazard function
What conditions must the parameters α and β meet for [latex]h(t)[/latex] to be a legitimate hazard function for a random lifetime T?
-
4.6 Jordan has designed a new screwdriver. Its lifetime, measured in years, follows a distribution with survivor function
where λ and [latex]\kappa[/latex] are positive parameters. If [latex]\kappa = 1 / 2[/latex] and [latex]\lambda = 1 / 7[/latex], find the probability that a screwdriver that is still functioning after 5 years of use will last another 3 years.
-
4.7 Let the time to failure of a bar code reader have survivor function
where [latex]\theta > 0[/latex]. If Ellen places n bar code readers on test simultaneously at time [latex]t = 0[/latex], find the expected number that fail by time [latex]t_0[/latex].
-
4.8 The lifetime of a motor, in years, is a continuous random variable with probability density function
Find the warranty period so that 5% of the motors will fail during the warranty period on average.
-
4.9 Carrie purchases a hammer whose lifetime T is a random variable with survivor function
where λ is a positive scale parameter and [latex]\kappa[/latex] is a positive shape parameter. Assuming that [latex]\lambda = 0.001[/latex] and [latex]\kappa = 2[/latex], find [latex]P(T > 80 \, | \, T > 50)[/latex].
-
4.10 Let the lifetime T have hazard function
for positive parameter λ. Find the associated survivor function [latex]S(t)[/latex].
-
4.11 Consider a random lifetime T with survivor function
Give a variate generation algorithm for this probability distribution.
-
4.12 Show that
can also be found by
for any continuous random variable T with nonnegative support and a finite population mean whenever [latex]\lim_{\, {t} \, \to \, \infty} \, t \, S(t) = 0[/latex].
-
4.13 Consider the random variable T with hazard function
- Find [latex]S(t)[/latex].
- Find the median of T.
- Find the 95th percentile of T.
-
4.14 Let T be a random variable with hazard function
where [latex]\kappa[/latex] is a positive parameter.
- Use numerical methods to determine a value of [latex]\kappa[/latex] such that [latex]E[T] = 1/5[/latex].
- Conduct a Monte Carlo simulation experiment that supports the value of [latex]\kappa[/latex] determined in part (a).
-
4.15 The random variable T has hazard function
Find [latex]E[T][/latex].
-
4.16 An insurance company issues a 30-month warranty on an automobile transmission. Lisa has purchased a 30-month warranty on her transmission and has not made a claim during the 30 months. She would like to purchase a 12-month extension to the warranty. This insurance company will pay a fixed $5000 for a new transmission on the extended warranty if her transmission fails within the next 12 months. Let the continuous random variable T denote the lifetime of Lisa’s transmission, measured in months, from the date of the purchase of the automobile. The survivor function of T is [latex]S(t)[/latex]. Find an expression for the expected payment that the insurance company will make on Lisa’s extended warranty.
-
4.17 Find the population skewness and kurtosis for an exponential(λ) random variable.
-
4.18 Which of the following lifetimes is the best candidate for being well approximated by an exponential distribution?
- The burning time for a particular type of candle.
- The duration of a woman’s pregnancy associated with her newborn baby.
- The duration of a strike.
- The duration of a men’s haircut by John at John’s barbershop.
- The breaking strength of a particular type of yarn.
-
4.19 Tami purchases a battery whose lifetime T is [latex]\hbox{exponential}(\lambda)[/latex], for some fixed, positive failure rate λ. The battery is placed in storage on the interval [latex][0, \, t_0][/latex], where [latex]t_0[/latex] is a fixed, positive constant time value, then monitored continuously for failure thereafter. Thus, the time to detect failure is [latex]X = \max\{ T, \, t_0 \}[/latex]. Find [latex]E[X][/latex].
-
4.20 Consider the continuous random variables T1 and T2, each with positive support. Let [latex]S_1(t)[/latex] denote the survivor function of T1 and [latex]S_2(t)[/latex] denote the survivor function of T2. When [latex]{S_1(t) \ge S_2(t)}[/latex] for all values of [latex]t \ge 0[/latex], T1 is said to “stochastically dominate” T2. This is one way of showing the superiority of the probability distribution of T1 over the probability distribution of T2. One measure of the difference between T1 and T2 is the Kolmogorov metric
Calculate the value of D for the independent random variables [latex]T_1 \sim \hbox{exponential}(\lambda_1)[/latex] and [latex]T_2 \sim \hbox{exponential}(\lambda_2)[/latex], where [latex]\lambda_1 < \lambda_2[/latex].
-
4.21 Rosie purchases a light bulb whose lifetime follows an exponential distribution. If the mean lifetime is one year longer than the median lifetime, find the value of the mean lifetime.
-
4.22 Marian purchases 30 sixty-watt light bulbs, each having a lifetime which is exponentially distribution with a mean of 1000 hours. If she places the 30 bulbs on a life test without replacement upon failure, find the probability that 10 or fewer of these light bulbs survive to 1200 hours.
-
4.23 An automobile insurance policy is structured as follows. For claims below $1000, the policyholder bears the entire cost of the claim. For claims between $1000 and $2000, the policyholder bears the first $1000 of the claim and the policy pays any additional amount. For claims over $2000, the policyholder bears the first $1000 of the claim and the policy pays $1000 plus half of the amount that exceeds $2000. The distribution of a claim T has the exponential distribution with mean $3000. Find the cumulative distribution function of the reimbursement amount that the insurance company pays on a claim.
-
4.24 Let [latex]T_1, \, T_2, \, \ldots , \, T_5[/latex] be independent and identically distributed exponential(λ) random variables.
- Find the probability density function of the second order statistic [latex]T_{(2)}[/latex].
- Find [latex]P\left( T_{(2)} \le 1 / \lambda \right)[/latex].
-
4.25 Let T1, T2, T3, be independent and identically distributed exponential(λ) random variables. Find the 96th percentile of the random variables:
- [latex]3 \min\{T_1, \, T_2, \, T_3 \}[/latex],
- [latex]T_1 + T_2 - T_3[/latex].
-
4.26 Troy is a bicyclist. His bike has a front wheel with eight spokes. The wheel is in the failed state when two consecutive spokes have failed. The initial lifetime distributions of the eight spokes are independent and identically distributed exponential random variables with failure rates of one failure per year. When a spoke fails, the failure rate of the two adjacent operating spokes doubles. Conduct a Monte Carlo simulation experiment to estimate the population mean time to wheel failure (considering only the spokes) to two-digit accuracy.
-
4.27 For the Weibull random lifetime T, show that
regardless of the value of [latex]\kappa[/latex].
-
4.28 Find the population skewness and kurtosis of a Weibull([latex]\lambda, \, \kappa[/latex]) random variable.
-
4.29 Find the value of the shape parameter in the Weibull distribution associated with a population skewness of zero.
-
4.30 Drea is using a graphics design software package that has a Weibull time to failure. Find the mode of the time to failure distribution. For which parameter values is this value the mode? Find the probability that the software package is still functioning at the mode value.
-
4.31 Let [latex]T \sim \hbox{Weibull}(\lambda, \, \kappa)[/latex].
- Find expressions for the mean, median, and mode of T. (Hint: they might not all be closed-form.)
- Find parameter values associated with the following three cases: the median and mode of the distribution are equal; the mean and median of the distribution are equal; the mean and mode of the distribution are equal.
-
4.32 Katherine designs a scanner and desires a one-month reliability of 0.8. She finds that the failure time of the scanner has a Weibull distribution with parameters [latex]\lambda = 8.33[/latex] and [latex]\kappa = 0.334[/latex], with time measured in months. Unfortunately, she finds that the one-month reliability is
which is clearly unacceptable. Fortunately, this Weibull distribution has a decreasing failure rate, so she knows that if she burns in the scanners, she can increase their one-month reliability. How long should she burn in the scanners to achieve a one-month reliability of 0.8 for scanners that survive the test? What fraction of the scanners placed on the burn-in test will fail during the test?
-
4.33 Statistical applications involving the Weibull distribution can benefit from reparameterizing the distribution. One such reparameterization replaces the scale parameter λ with a particular fractile of the distribution. More specifically, let p0 be a prescribed constant satisfying [latex]{0 < p_0 < 1}[/latex]. Denote the associated fractile of the Weibull distribution as [latex]t_{p_0}[/latex]. Perform the necessary algebra to write the survivor function of the reparameterized Weibull distribution in terms of the parameters [latex]t_{p_0}[/latex] and [latex]\kappa[/latex].
-
4.34 Alex purchases a laptop computer with a lifetime T, in years, which has a Weibull distribution with [latex]\lambda = 0.2[/latex] and [latex]\kappa = 2[/latex]. The laptop computer can be purchased for $600. The manufacturer of the laptop provides a full refund if the laptop fails within the first year after purchase, a one-third refund if the laptop fails during the second year after purchase, and no refund if the laptop fails thereafter. What is the expected refund on a laptop?
-
4.35 Steve takes three generators to a work site. He will use the three generators in a cold standby system to provide electrical power. The lifetimes of the generators are exponentially distributed with mean 1000 hours. Find the variance of the total amount of time that electrical power can be supplied by the generators.
-
4.36 Find [latex]E \left[ T^r \right][/latex] for [latex]r = 1, \, 2, \, \ldots[/latex] for a log logistic random variable.
-
4.37 Find the population skewness and kurtosis of a log logistic random variable.
-
4.38 Lindsay purchases a jack hammer. Let the lifetime of an item be defined by a special case of the log logistic distribution with survivor function
where λ is a positive scale parameter. If the item has been operating for a time units, find
- the probability it will last another r time units,
- the expected remaining time to failure.
-
4.39 Consider the random variable X having the logistic distribution with location parameter η, positive scale parameter [latex]\rho > 0[/latex], and probability density function
Show that [latex]e^{\kern 0.04em X}[/latex] has the log logistic distribution.
-
4.40 Derive [latex]\lim_{\, {t} \, \to \, \infty} h(t)[/latex] for the log normal distribution.
-
4.41 Many life insurance companies offer a “last-to-die” policy for couples or business partners that pays out when the second of the two individuals dies. These policies are often purchased to pay tax liabilities on small businesses. Assume that David, age 40, and his wife Laura, age 35, celebrate their mutual birthday by purchasing a one-year, $100,000 term last-to-die policy. Find, to the nearest penny, the revenue-neutral premium (that is, where the premium equals the expected payout). For simplicity, assume that
- all new-born baby boys have Weibull random lifetimes with [latex]\lambda = 1 / 65[/latex] and [latex]\kappa = 3 / 2[/latex],
- all new-born baby girls have exponential power random lifetimes with [latex]\lambda = 1 / 12[/latex] and [latex]\kappa = 1 / 2[/latex],
- health care, lifestyle, environmental factors, etc. remain constant throughout David and Laura’s lifetimes,
- there is no overhead or profit associated with the premium,
- the prevailing interest rate during the next year is 0%, and
- their two lifetimes are independent.
-
4.42 Meghan purchases a book stand for a rare book, which has lifetime T. If T has the log logistic distribution, [latex]{S(1) = 1 / 5}[/latex] and [latex]{S(3) = 1 / 37}[/latex], find [latex]S(2)[/latex].
-
4.43 Joanna purchases a food truck whose lifetime is a continuous random variable T with the power distribution, having probability density function
where α is a positive scale parameter and β is a positive shape parameter. Find the median of T.
-
4.44 Summer and Brigid are conducting a study concerning the random time T required to reshelve a book after it has been returned to a library. The time between the return of a book and the time it is reshelved has a special case of the extreme value distribution with survivor function
For real constants a and b satisfying [latex]a < b[/latex], find [latex]P(a < T < b)[/latex].
-
4.45 Daneen is modeling the lifetimes of light bulbs (in years) with the proportional hazards model with [latex]q = 2[/latex] covariates: wattage ([latex]z_1[/latex]) and operating temperature in degrees Fahrenheit ([latex]z_2[/latex]). The baseline distribution is exponential with a failure rate of 1.1 failures per year and the log-linear form of the link function [latex]\psi ( {\bf z})[/latex] is used. If previous data has shown that the associated regression coefficients are [latex]\beta_1 = 0.003[/latex] and [latex]\beta_2 = 0.004[/latex], what is the expected time to failure of a 60-watt bulb operating in a constant 72°F environment?
-
4.46 In a log logistic regression model with a single covariate z, the lifetime T can be expressed as
where β0 and β1 are regression parameters, [latex]\theta > 0[/latex] is a parameter of the model, and Y has probability density function
- Find the survivor function of T for one particular value of the covariate z; that is, find [latex]S_{T \, | \, Z = z}(t \, | \, Z = z)[/latex].
- The odds ratio
gives the odds that an item fails by time t for one particular value of the covariate z. Calculate the odds ratio for the log logistic regression model.
- Consider two different items with covariates z1 and z2. Prove that the quotient of their odds ratios is independent of t for any time [latex]t > 0[/latex].
-
4.47 Consider the baseline hazard function
In a proportional hazards model, find the probability that an item with covariates [latex]{\boldsymbol z}[/latex] and link function [latex]\psi ({\boldsymbol z})[/latex] survives to time t.
-
4.48 A proportional hazards model is applied to a lifetime that has a single binary covariate z with regression coefficient β, link function [latex]\psi (z) = e^{\kern 0.04em \beta z}[/latex], and Weibull baseline hazard function. Find
- the survivor function for the time to failure,
- the mean time to failure when [latex]z = 0[/latex],
- the mean time to failure when [latex]z = 1[/latex].
-
4.49 Ali purchases a freezer with a lifetime that is well approximated by the proportional hazards model with [latex]q = 2[/latex] covariates: external temperature z1 (measured in degrees Celsius) and humidity z2. Assume that the Weibull baseline distribution and a log-linear link function are used.
- What would you expect the sign (positive or negative) of [latex]\hat{\beta}_1[/latex] to be if a large sample of failure times and associated covariates was collected? Explain your reasoning.
- Find the probability that such a component survives to time t for any covariate vector [latex]{\boldsymbol z}[/latex] and regression coefficients [latex]\boldsymbol{\beta}[/latex].
-
4.50 Write a few sentences describing the suitability of the link functions
for a proportional hazards model with [latex]q = 2[/latex] covariates.
-
4.51 Consider the Cox proportional hazards model
with [latex]q = 2[/latex]covariates, z1 and z2, which includes an interaction term between the covariates. The link function assumes the log linear formml:
Find the ratio of the hazard function for covariates z1 and z2 to the hazard function for covariates z1 and [latex]z_2 + 5[/latex].

