Chapter 6: Topics in Survival Analysis

Lawrence M. Leemis

Chapter 6 Topics in Survival Analysis

The previous two chapters have introduced some probabilistic models and statistical methods that arise in survival analysis. This chapter surveys some topics that would be a part of a full-semester course in survival analysis. The first section considers nonparametric methods that arise in survival analysis, with a focus on estimating the survivor function. The empirical survivor function is used in the case of a complete data set and the Kaplan–Meier product–limit estimator is used in the case of a right-censored data set. These methods require no parametric assumptions from the modeler. The log-rank test, which is a nonparametric hypothesis test used to compare two survivor functions, is also introduced. The second section introduces the competing risks model, which is appropriate when multiple risks compete for the lifetime of an item. The third section considers not just a single failure time, but items which undergo multiple failures, such as an automobile.

6.1 Nonparametric Methods

Nonparametric methods require no parametric assumptions (for example, exponential or Weibull lifetime models) concerning the lifetime of an item. The emphasis is to let the data speak for itself, rather than approximating the lifetime distribution by a parametric model. In many applications, the modeler does not have any clues revealing an appropriate parametric model, so a nonparametric approach is warranted. The first subsection considers the estimation of the survivor function for a complete data set of n items placed on test. The second subsection considers the estimation of the survivor function for a randomly right-censored data set of n items placed on test. Two different types of derivations both lead to the Kaplan–Meier product–limit estimator. The third subsection considers the problem of comparing the estimated survivor functions of two different types of items. In the reliability setting, this might be to compare the lifetimes of Product A versus Product B. In the biostatistical setting, this might be to compare the survival times of patients undergoing radiation and chemotherapy for a particular type of cancer.

6.1.1 Survivor Function Estimation for Complete Data Sets

Consider the nonparametric estimation of the survivor function from a complete data set of n lifetimes with no ties. The risk set [latex]R(t)[/latex] contains the indexes of all items at risk just prior to time t. Let [latex]n(t) = |R(t)|[/latex] be the cardinality of [latex]R(t)[/latex]. In other words, [latex]n(t)[/latex] is the number of elements in [latex]R(t)[/latex]. The simplest and most popular nonparametric estimate for the survivor function is

$\begin{array}{l} \hat{S} (t) = \frac{n (t)}{n} t \geq 0, \end{array}$

which is often referred to as the empirical survivor function. This step function takes a downward step of size [latex]1 / n[/latex] at each observed lifetime. It is also the survivor function corresponding to a discrete distribution with n equally likely mass values. Ties are not difficult to adjust for because the formula for [latex]\hat{S}(t)[/latex] remains the same, but the function will take a downward step of [latex]d / n[/latex] if there are d tied observations at a particular time value.

When there are no ties in the data set, one method for determining asymptotically exact confidence intervals for the survivor function is based on the normal approximation to the binomial distribution. Recall that a binomial random variable X models the number of successes in n independent Bernoulli trials, each with probability of success p. The expected value and population variance of the number of successes are [latex]E[X] = np[/latex] and [latex]V[X] = np(1-p)[/latex]. The fraction of successes, [latex]X / n[/latex], on the other hand, has expected value [latex]E[X/n] = p[/latex] and population variance [latex]V[X/n] = p(1-p) / n[/latex].

Survival to a fixed time t can be considered a Bernoulli trial for each of the n items on test. An item either survives to time t or it does not. Thus, the number of items that survive to time t, which is [latex]n(t)[/latex], has the binomial distribution with parameters n and probability of success [latex]S(t)[/latex], where success is defined to be survival to time t. The empirical survivor function introduced earlier, [latex]\hat{S}(t) = n(t) / n[/latex], is the fraction of successes, which has expected value

$\begin{array}{l} E [\hat{S} (t)] = S (t) \end{array}$

and population variance

$\begin{array}{l} V [\hat{S} (t)] = \frac{S (t) (1 - S (t))}{n} . \end{array}$

So [latex]\hat S(t)[/latex] is an unbiased and consistent estimator of [latex]S(t)[/latex] for all values of t. Furthermore, when the number of items on test n is large and [latex]S(t)[/latex] is not too close to 0 or 1, the binomial distribution assumes a shape that is closely approximated by a normal probability density function and thus can be used to find an interval estimate for [latex]S(t)[/latex]. Notice that such an interval estimate is most accurate, in terms of coverage, around the median of the distribution because the normal approximation to the binomial distribution works best when the probability of success is about [latex]1/2[/latex], where the binomial distribution is symmetric. Replacing [latex]S(t)[/latex] by [latex]\hat S(t)[/latex] in the population variance formula, an asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for the probability of survival to time t is

$\begin{array}{l} \hat{S} (t) - z_{α / 2} \sqrt{\frac{\hat{S} (t) (1 - \hat{S} (t))}{n}} < S (t) < \hat{S} (t) + z_{α / 2} \sqrt{\frac{\hat{S} (t) (1 - \hat{S} (t))}{n}} . \end{array}$

This confidence interval is also appropriate when there are tied observations, although it becomes more approximate as the number of ties increases. Confidence limits greater than 1 or less than 0 are typically truncated, as illustrated in the following example.

Example 6.1 For the ball bearing data set from Example 5.5 with [latex]n = 23[/latex] bearings placed on test until failure, find a nonparametric survivor function estimator and an approximate two-sided 95% confidence interval for the probability that a ball bearing will survive 50,000,000 cycles.

Recall that the ball bearing failure times in 10⁶ revolutions are

$\begin{array}{l} 17.88 28.92 33.00 41.52 42.12 45.60 48.48 51.84 51.96 \\ 54.12 55.56 67.80 68.64 68.64 68.88 84.12 93.12 98.64 \\ 105.12 105.84 127.92 128.04 173.40 . \end{array}$

The nonparametric survivor function estimate [latex]\hat S(t)[/latex] is shown as the solid line in Figure 6.1. In this figure and others, the downward steps in [latex]\hat S(t)[/latex] have been connected by vertical lines. Many analysts find this useful when visually comparing a nonparametric estimator of [latex]S(t)[/latex] to a fitted parametric model. The empirical survivor function takes a downward step of size [latex]1 / 23[/latex] at each data value, with the exception of the tied value, 68.64, where it takes a downward step of [latex]2 / 23[/latex]. By convention, the survivor function estimate cuts off after the largest observed failure time. Since the data is given in 10⁶ revolutions, a point estimate for the survivor function at [latex]t = 50[/latex] is

$\begin{array}{l} \hat{S} (50) = \frac{16}{23} = 0.6957, \end{array}$

and an approximate two-sided 95% confidence interval for the survivor function at [latex]t = 50[/latex] is

$\begin{array}{l} \hat{S} (50) - 1.96 \sqrt{\frac{\hat{S} (50) (1 - \hat{S} (50))}{23}} < S (50) < \hat{S} (50) + 1.96 \sqrt{\frac{\hat{S} (50) (1 - \hat{S} (50))}{23}}, \end{array}$

which reduces to

$\begin{array}{l} 0.5076 < S (50) < 0.8837 . \end{array}$

This process can be performed for all t values, yielding the approximate two-sided 95% confidence bands for [latex]S(t)[/latex] given by the dashed lines in Figure 6.1. The confidence bands are truncated at 0 and 1. Also, the lower confidence band appears to be absent prior to the first observed failure at [latex]t_{(1)}[/latex] = 17.88. This is due to the fact that [latex]\hat{S}(t)[/latex] is 1 for t values between 0 and the first failure time, so the upper and lower confidence limits are both equal to 1.

Figure 6.1: Nonparametric survivor function estimate for the ball bearing data set.

Long Description for Figure 6.1

The horizontal axis t ranges from 0 to 200 in increments of 50 units. The vertical axis S of t ranges from 0.0 to 1.0 in increments of 0.2 units. The downward step function with 19 steps decreases rapidly from 1.0 to 0.5 as time increases from 0 to 50 units. It then decreases gradually to 0.1 as time increases to 150 units. The two sided 95 percent confidence bands are drawn along with the survivor function as dashed lines, one lies above, and the other lies below. All three follow the same pattern and appear parallel. The one above the survivor function decreases from 1.0 to 0.15 as t increases from 0 to 150. The one below the survivor function decreases rapidly from 0.9 to 0.2, whilst the t increases from 25 to 75, and then decreases gradually and maintains 0.0 for t equals 100 to 200. All data are estimated.

Even though the confidence interval for [latex]S(t)[/latex] from a complete data set of n lifetimes used in the previous example is intuitive and easy to compute, its performance in terms of its actual coverage is notoriously poor. One particular instance of its poor performance occurs at time [latex]t = 10[/latex], where the approximate two-sided 95% confidence interval has lower and upper bounds equal to 1. It is known as the Wald confidence interval, and its use is generally frowned upon because better alternatives exist. Four such alternatives are outlined (without derivation) in the next four paragraphs.

The approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] Clopper–Pearson confidence interval for [latex]S(t)[/latex] has bounds that can be expressed as the fractiles of beta distributions:

$\begin{array}{l} B_{n (t), n - n (t) + 1, 1 - α / 2} < S (t) < B_{n (t) + 1, n - n (t), α / 2}, \end{array}$

for [latex]n(t) = 0, \, 1, \, 2, \, \ldots, \, n[/latex], where the first two values in the subscripts of B are the parameters of the beta distribution and the third value in the subscripts is a right-hand tail probability. The Clopper–Pearson confidence interval bounds can also be written as functions of fractiles of the F distribution.

The bounds on the Wilson–score approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]S(t)[/latex] are

$\begin{array}{l} \frac{1}{1 + z_{α / 2}^{2} / n} [\hat{S} (t) + \frac{z_{α / 2}^{2}}{2 n} \pm z_{α / 2} \sqrt{\frac{\hat{S} (t) (1 - \hat{S} (t))}{n} + \frac{z_{α / 2}^{2}}{4 n^{2}}}], \end{array}$

where [latex]z_{\alpha/2}[/latex] is the [latex]1 - \alpha / 2[/latex] fractile of the standard normal distribution. The center of the Wilson–score confidence interval is

$\begin{array}{l} \frac{\hat{S} (t) + z_{α / 2}^{2} / (2 n)}{1 + z_{α / 2}^{2} / n}, \end{array}$

which is a weighted average of the point estimator [latex]\hat S(t) = n(t) / n[/latex] and [latex]1 / 2[/latex], with more weight on [latex]\hat S(t)[/latex] as n increases.

The Jeffreys approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] interval estimate for [latex]S(t)[/latex] is a Bayesian credible interval that uses a Jeffreys non-informative prior distribution for [latex]S(t)[/latex]. As was the case with the Clopper–Pearson confidence interval, the bounds of the Jeffreys interval for [latex]S(t)[/latex] are fractiles of beta random variables:

$\begin{array}{l} B_{n (t) + 1 / 2, n - n (t) + 1 / 2, 1 - α / 2} < S (t) < B_{n (t) + 1 / 2, n - n (t) + 1 / 2, α / 2} \end{array}$

for [latex]n(t) = 1, \, 2, \, \ldots, \, n - 1[/latex]. When [latex]n(t) = 0[/latex], the lower bound is set to zero and the upper bound calculated using the formula above; when [latex]n(t) = n[/latex], the upper bound is set to one and the lower bound calculated using the formula above.

The bounds of the Agresti–Coull approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]S(t)[/latex] are

$\begin{array}{l} \tilde{S} (t) \pm z_{α / 2} \sqrt{\frac{\tilde{S} (t) (1 - \tilde{S} (t))}{\tilde{n}}}, \end{array}$

where [latex]\tilde n = n + z_{\alpha / 2}^2[/latex] and [latex]\tilde S(t) = \big(n(t) + z_{\alpha / 2}^2 / 2 \big)/ \tilde n[/latex]. In the special case of [latex]\alpha = 0.05[/latex], if one is willing to round [latex]z_{\alpha / 2} = 1.96[/latex] to 2, this interval can be interpreted as “add two successes and add two failures and use the Wald confidence interval formula.”

Example 6.2 Find the Clopper–Pearson, Wilson–score, Jeffreys, and Agresti–Coull approximate two-sided 95% confidence intervals for [latex]S(50)[/latex] for the ball bearing lifetimes from Example 5.5.

As in the previous example, the point estimator for [latex]S(50)[/latex] is [latex]\hat S(50) = 16/23 = 0.6957[/latex]. Using the parameters [latex]n = 23[/latex], [latex]n(50) = 16[/latex], [latex]\alpha = 0.05[/latex], the approximate two-sided 95% Clopper–Pearson, Wilson–score, Jeffreys, and Agresti–Coull confidence intervals for [latex]S(50)[/latex] are given in Table 6.1. The R code to compute these confidence intervals is given below. All confidence intervals are calculated using the binomTest function from the conf package.

Table 6.1: Approximate 95% confidence intervals for [latex]S(50)[/latex] for the ball bearing data.
Method	95% confidence interval
Wald	[latex]0.508 < S(50) < 0.884[/latex]
Clopper–Pearson	[latex]0.471 < S(50) < 0.868[/latex]
Wilson–score	[latex]0.491 < S(50) < 0.844[/latex]
Jeffreys	[latex]0.493 < S(50) < 0.852[/latex]
Agresti–Coull	[latex]0.489 < S(50) < 0.846[/latex]

The confidence interval bounds vary significantly between the techniques. The narrowest confidence interval is the Wilson–score and the widest confidence interval is the Clopper–Pearson. Some analysts prefer the Clopper–Pearson confidence interval because it is conservative in the sense that its actual coverage always exceeds the stated coverage (which is 95% in this example) for all values of [latex]S(t)[/latex]. This implies that you will never claim more precision with your confidence interval than is implied by the stated coverage. The Clopper–Pearson 95% confidence intervals for [latex]S(t)[/latex] for all values of t are plotted as confidence bands in Figure 6.2. Unlike the Wald confidence bands depicted in Figure 6.1, these confidence intervals are not symmetric about the associated point estimators given by the solid lines, and this non-symmetry is particularly pronounced at the extremes.

Figure 6.2: Clopper–Pearson confidence bands for the ball bearing data set.

Long Description for Figure 6.2

The horizontal axis t ranges from 0 to 200 in increments of 50 units. The vertical axis S of t ranges from 0.0 to 1.0 in increments of 0.2 units. The downward step function with 19 steps decreases rapidly from 1.0 to 0.5 as time increases from 0 to 50 units. It then decreases gradually to 0.1 as time increases to 150 units. The Clopper Pearson confidence bands are drawn, along with the survivor function, as dashed lines, one above and one below. All three follow almost the same pattern, and appear parallel. The one above the survivor function decreases rapidly from 1.0 to 0.7 as t increases from 0 to 50, then decreases progressively to 0.3 as t increases to 150. The one below the survivor function decreases rapidly from 0.85 to 0.2 as t increases from 0 to 50, and then decreases gradually and maintains 0.0 for t equals 120 to 200. All data are estimated.

There are dozens of confidence interval procedures for calculating an approximate confidence interval for [latex]S(t)[/latex]. The intervals illustrated in the previous example were selected because of (a) their popularity with statisticians, (b) their availability in statistical software packages, and (c) their statistical properties, particularly their actual coverage. The four confidence interval procedures illustrated in the previous example all possess the following properties.

For a fixed number of items on test n, the confidence intervals are complementary for any particular [latex]n(t)[/latex] and [latex]n - n(t)[/latex].
The confidence intervals are asymptotically exact for [latex]0 < S(t) < 1[/latex].
The confidence intervals do not degenerate to a confidence intervals of width zero for [latex]n(t) = 0[/latex] or [latex]n(t) = n[/latex] as was the case with the Wald confidence interval.

This concludes the discussion concerning finding point and interval estimators for [latex]S(t)[/latex] from a complete data set of lifetimes. We now introduce techniques for estimating [latex]S(t)[/latex] from a right-censored data set.

6.1.2 Survivor Function Estimation for Right-Censored Data Sets

The general case in which there are both ties and right-censored data values is now considered. Some new notation must be established in order to derive the nonparametric estimator for [latex]S(t)[/latex]. As before, assume that n items are on test. Let [latex]y_1 < y_2 < \cdots < y_k[/latex] denote the k distinct observed failure times, and let d_j denote the number of observed failures at y_j, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Let [latex]n_j = n(y_j)[/latex] denote the number of items on test just before time y_j, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex], and it is customary to include any values that are right censored at y_j in this count.

The search for a survivor function estimator begins by assuming that the data arose from a discrete distribution with mass values [latex]y_1 < y_2 < \cdots < y_k[/latex]. For a discrete distribution, [latex]h(y_j)[/latex] is a conditional probability with interpretation [latex]h(y_j) = P( T = y_j \,|\, T \ge y_j )[/latex]. The survivor function can be written in terms of the hazard function at the mass values as

$\begin{array}{l} S (t) = \prod_{j | y_{j} \leq t} [1 - h (y_{j})] t \geq 0. \end{array}$

Thus, a reasonable estimator for [latex]S(t)[/latex] is [latex]\prod_{j \, | \, y_j < \, t} \big[1 - \hat{h}(y_j)\big][/latex], which reduces the problem of estimating the survivor function to that of estimating the hazard function at each mass value. An appropriate element in the likelihood function at mass value y_j is

$\begin{array}{l} h (y_{j})^{d_{j}} [1 - h (y_{j})]^{n_{j} - d_{j}} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. The above expression is correct because d_j is the number of failures at y_j, [latex]h(y_j)[/latex] is the conditional probability of failure at y_j, [latex]n_j - d_j[/latex] is the number of items on test not failing at y_j, and [latex]1 - h( y_j )[/latex] is the probability of failing after time y_j conditioned on survival to time y_j. Thus, the likelihood function for [latex]h (y_1), \, h(y_2), \, \ldots, \, h(y_k)[/latex] is

$\begin{array}{l} L (h (y_{1}), h (y_{2}), \dots, h (y_{k})) = \prod_{j = 1}^{k} h (y_{j})^{d_{j}} [1 - h (y_{j})]^{n_{j} - d_{j}} \end{array}$

and the log likelihood function is

$\begin{array}{l} \ln L (h (y_{1}), h (y_{2}), \dots, h (y_{k})) = \sum_{j = 1}^{k} {d_{j} \ln h (y_{j}) + (n_{j} - d_{j}) \ln [1 - h (y_{j})]} . \end{array}$

The ith element of the score vector is

$\begin{array}{l} \frac{\partial \ln L (h (y_{1}), h (y_{2}), \dots, h (y_{k}))}{\partial h (y_{i})} = \frac{d_{i}}{h (y_{i})} - \frac{n_{i} - d_{i}}{1 - h (y_{i})} \end{array}$

for [latex]i = 1, \, 2, \, \ldots, \, k[/latex]. Equating this element of the score vector to zero and solving for [latex]h ( y_i )[/latex] yields the maximum likelihood estimate

$\begin{array}{l} \hat{h} (y_{i}) = \frac{d_{i}}{n_{i}}, \end{array}$

for [latex]i = 1, \, 2, \, \ldots, \, k[/latex]. This estimate for [latex]\hat{h} (y_i)[/latex] is sensible because d_i of the n_i items on test at time y_i fail, so the ratio of d_i to n_i is an appropriate estimate of the conditional probability of failure at time y_i. This derivation may strike a familiar chord because at each time y_i, estimating [latex]h( y_i )[/latex] with d_i divided by n_i is equivalent to estimating the probability of success (that is, failing at time y_i) for each of the n_i items on test. Thus, this derivation is equivalent to finding the maximum likelihood estimators for the probability of success for k binomial random variables.

Using this particular estimate for the hazard function at y_i, the survivor function estimate becomes

$\begin{array}{l} \hat{S} (t) = \prod_{j | y_{j} \leq t} [1 - \hat{h} (y_{j})] = \prod_{j | y_{j} \leq t} [1 - \frac{d_{j}}{n_{j}}], \end{array}$

for [latex]t \ge 0[/latex], commonly known as the Kaplan–Meier or product–limit estimator. When the largest data value recorded corresponds to a failure, the product–limit estimator drops to zero; when the largest data value recorded corresponds to a right-censored observation, a common convention is to cut off the product–limit estimator at the current positive value of [latex]\hat S(t)[/latex]. The original journal article by American mathematician Edward Kaplan and American statistician Paul Meier in 1958 that established the product–limit estimator is one of the most heavily cited papers in the statistics literature. The following example illustrates the process of calculating the product–limit estimate.

Example 6.3 Use the product–limit estimator to calculate a point estimate of the probability that a remission time in the treatment group in the 6–MP clinical trial described in Example 5.6 exceeds 14 weeks. In other words, estimate [latex]S(14)[/latex] using the Kaplan–Meier estimator.

The data set contains [latex]n = 21[/latex] patients on test, [latex]r = 9[/latex] observed failures (leukemia relapses), and [latex]k = 7[/latex] distinct observed failure times. The data values, in weeks, are

$\begin{array}{l} 6 6 6 6^{*} 7 9^{*} 10 10^{*} 11^{*} 13 16 \\ 17^{*} 19^{*} 20^{*} 22 23 25^{*} 32^{*} 32^{*} 34^{*} 35^{*} . \end{array}$

Table 6.2 gives the values of y_j, d_j, n_j, and [latex]1 - d_j / n_j[/latex] for [latex]j = 1, \, 2, \, \ldots, \, 7[/latex]. The product–limit survivor function estimate at [latex]t = 14[/latex] weeks is

$\begin{array}{l} \hat{S} (14) & = \prod_{j | y_{j} \leq 14} [1 - \frac{d_{j}}{n_{j}}] \\ = [1 - \frac{3}{21}] [1 - \frac{1}{17}] [1 - \frac{1}{15}] [1 - \frac{1}{12}] \\ = \frac{176}{255} \\ = 0.69 . \end{array}$

Table 6.2: Product–limit calculations for 6–MP treatment case.
j	y_j	d_j	n_j	$1 - \frac{d_{j}}{n_{j}}$
1	6	3	21	$1 - \frac{3}{21}$
2	7	1	17	$1 - \frac{1}{17}$
3	10	1	15	$1 - \frac{1}{15}$
4	13	1	12	$1 - \frac{1}{12}$
5	16	1	11	$1 - \frac{1}{11}$
6	22	1	7	$1 - \frac{1}{7}$
7	23	1	6	$1 - \frac{1}{6}$

The product–limit survivor function estimate for all t values is plotted in Figure 6.3. Downward steps occur at the [latex]k = 7[/latex] observed failure times. Some software packages place a vertical hash mark on the Kaplan–Meier estimate to highlight censored values that occur between observed failure times; these occur at times 9, 11, 17, 19, 20, 25, 32, and 34 in Figure 6.3. The effect of censored observations in the survivor function estimate is a larger downward step at the next subsequent observed failure time. If there is a tie between an observed failure time and censoring time (as there is at time 6 in this example) the standard convention of including the censored value(s) in the risk set when computing the number of items at risk means that there will be a larger downward step in the survivor function estimate following the tied value. Since the last observed data value, 35*, corresponds to a right-censored observation, the survivor function estimate is truncated at time 35 and is assumed to be undefined for [latex]t > 35[/latex].

Figure 6.3: Product–limit survivor function estimate for the 6–MP treatment group.

Long Description for Figure 6.3

The horizontal axis t ranges from 0 to 35 in increments of 5 units. The vertical axis S of t ranges from 0.0 to 1.0 in increments of 0.2 units. The downward step function with 8 steps decreases from 1.0 to 0.4, whilst the t increases from 0 to 35. The first step is from t equals 0 to 5, and the last step is from t equals 23 to 35, which are the longest steps. The vertical hash marks are placed on the Kaplan Meier estimate at the values of t equals 9, 11, 17, 19, 20, 25, 32, and 34.

The R code to generate this plot uses the survfit function from the survival package. The failure and censoring times [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] are held in the vector named time. The indicator variables [latex]\delta_1, \, \delta_2, \, \ldots, \, \delta_n[/latex] are held in the vector named status. The Surv function creates a survival object, which is used in the left-hand side of the formula argument passed to survfit. The right-hand side of the formula argument to survfit contains just 1 to indicate that there are no covariates being considered when computing the product–limit estimator for just the remission times in the treatment group. The summary function reveals the calculations used in estimating the product–limit estimate and the plot function generates a graph of the product–limit estimate, which is given in Figure 6.3.

There is a second and perhaps more intuitive way of deriving the product–limit estimator, often referred to as the “redistribute-to-the-right” algorithm. This technique begins by defining an initial probability mass function that apportions equal probability to each of the n data values. In subsequent passes through the data, this probability mass function estimate is modified as the probability is redistributed to the right, with special treatment given to right-censored observations. The algorithm is illustrated next on the 6–MP treatment group data set from Example 5.6.

Example 6.4 Implement the redistribute-to-the-right algorithm for calculating the Kaplan–Meier product–limit estimate of the survivor function for the remission time in the treatment group in the 6–MP clinical trial from Example 5.6.

For the [latex]n = 21[/latex] individuals in the treatment group for the 6–MP experiment, each failure or censoring time is initially assigned a mass value of [latex]1 / n[/latex] as follows:

6	6	6	6^*	7	9^*	10	10^*	11^*	13	…
$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	…

If there were no censored observations, the fractions would be the appropriate estimators for the probability mass function values. This probability mass function corresponds to the empirical survivor function described earlier in this section. Combining the three tied observed failures at [latex]t = 6[/latex] yields

6	6^*	7	9^*	10	10^*	11^*	13	…
$\frac{1}{7}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	$\frac{1}{21}$	…

As indicated earlier, there are mass values in the product–limit estimator only at observed failure times. Since the random censoring model is assumed, the mass associated with the individual whose remission time is right censored at 6 weeks can be split evenly among each of the 17 subsequent failure/censoring times:

$\begin{array}{l} \begin{array}{c} 6 & 6^{*} & 7 & 9^{*} & 10 & 10^{*} & 11^{*} & 13 & \dots \\ \frac{1}{7} & 0 & \frac{6}{119} & \frac{6}{119} & \frac{6}{119} & \frac{6}{119} & \frac{6}{119} & \frac{6}{119} & \dots \end{array} \end{array}$

because [latex]{1 \over 21} + {1 \over 17} \cdot {1 \over 21} = {6 \over 119}[/latex]. The probability mass function estimates at [latex]t = 6[/latex] and [latex]t = 7[/latex] have now been determined. The mass value [latex]{6 \over 119}[/latex] associated with the right censored observation at time 9 can be allocated among the 15 subsequent failure/censoring times as

$\begin{array}{l} \begin{array}{c} 6 & 6^{*} & 7 & 9^{*} & 10 & 10^{*} & 11^{*} & 13 & \dots \\ \frac{1}{7} & 0 & \frac{6}{119} & 0 & \frac{32}{595} & \frac{32}{595} & \frac{32}{595} & \frac{32}{595} & \dots \end{array} \end{array}$

because [latex]{6 \over 119} + {1 \over 15} \cdot {6 \over 119} = {96 \over 1785} = {32 \over 595}[/latex]. After allocating the mass at 10^* to the subsequent 13 data values and the mass at 11^* to the subsequent 12 data values, the estimator becomes

$\begin{array}{l} \begin{array}{c} 6 & 6^{*} & 7 & 9^{*} & 10 & 10^{*} & 11^{*} & 13 & \dots \\ \frac{1}{7} & 0 & \frac{6}{119} & 0 & \frac{32}{595} & 0 & 0 & \frac{16}{255} & \dots \end{array} \end{array}$

When this process is continued through all the data values, the resulting probability mass function defined on the observed failure times corresponds to the product–limit estimator. To check this for one specific time value, the survivor function estimate at time 14 is

$\begin{array}{l} \hat{S} (14) = 1 - \frac{1}{7} - \frac{6}{119} - \frac{32}{595} - \frac{16}{255} = \frac{176}{255} = 0.69, \end{array}$

which matches the result from the previous example.

Since we now have a point estimate for the survivor function, our attention turns to estimating its population variance in order to construct confidence intervals and conduct hypothesis tests. To find an estimate for the population variance of the product–limit estimate is significantly more difficult than for the uncensored case. The Fisher and observed information matrices require the following partial derivative of the score vector:

$\begin{array}{l} \frac{\partial^{2} \ln L (h (y_{1}), h (y_{2}), \dots, h (y_{k}))}{\partial h (y_{i}) \partial h (y_{j})} = - \frac{d_{i}}{h (y_{i})^{2}} - \frac{n_{i} - d_{i}}{(1 - h (y_{i}))^{2}} \end{array}$

when [latex]i = j[/latex] and 0 otherwise, for [latex]i = 1, \, 2, \, \ldots, \, k[/latex] and [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Both the Fisher and observed information matrices are diagonal. Replacing [latex]h (y_i)[/latex] by its maximum likelihood estimate, the diagonal elements of the observed information matrix are

$\begin{array}{l} {[- \frac{\partial^{2} \ln L (h (y_{1}), h (y_{2}), \dots, h (y_{k}))}{\partial h (y_{i})^{2}}]}_{h (y_{i}) = d_{i} / n_{i}} = \frac{n_{i}^{3}}{d_{i} (n_{i} - d_{i})} \end{array}$

for [latex]i = 1, \, 2, \, \ldots, \, k[/latex]. Using some approximations, an estimate for the variance of the estimated survivor function is

$\begin{array}{l} \hat{V} [\hat{S} (t)] = [\hat{S} (t)]^{2} \sum_{j | y_{j} \leq t} \frac{d_{j}}{n_{j} (n_{j} - d_{j})}, \end{array}$

commonly referred to as Greenwood’s formula. The formula can be used to find an asymptotically exact two-sided confidence interval for [latex]S(t)[/latex] by using the normal critical values as in the uncensored case:

$\begin{array}{l} \hat{S} (t) - z_{α / 2} \sqrt{\hat{V} [\hat{S} (t)]} < S (t) < \hat{S} (t) + z_{α / 2} \sqrt{\hat{V} [\hat{S} (t)]} . \end{array}$

As was the case with the Wald confidence interval for [latex]S(t)[/latex] in the case of a complete data set, the confidence interval bounds should be truncated when they are greater than 1 or less than 0, as illustrated in the next example.

Example 6.5 Use Greenwood’s formula to construct an approximate two-sided 95% confidence interval for the probability that a remission time in the treatment group in the 6–MP clinical trial described in Example 5.6 exceeds 14 weeks.

The point estimator for the probability of survival to time 14 from the previous two examples is [latex]\hat{S}(14) = 176 / 255 = 0.69[/latex]. The estimated variance of the survivor function estimator at time 14 via Greenwood’s formula is

$\begin{array}{l} \hat{V} [\hat{S} (14)] & = [\hat{S} (14)]^{2} \sum_{j | y_{j} \leq 14} \frac{d_{j}}{n_{j} (n_{j} - d_{j})} \\ = {(\frac{176}{255})}^{2} [\frac{3}{21 (21 - 3)} + \frac{1}{17 (17 - 1)} + \frac{1}{15 (15 - 1)} + \frac{1}{12 (12 - 1)}] \\ = 0.011 . \end{array}$

Thus, an estimate for the standard deviation of the survivor function estimate at [latex]t = 14[/latex] is [latex]\sqrt{0.011} = 0.11[/latex]. An approximate two-sided 95% confidence interval for [latex]S(14)[/latex] is

$\begin{matrix} \hat{S} (14) - z_{0.025} \sqrt{\hat{V} [\hat{S} (14)]} < S (14) < \hat{S} (14) + z_{0.025} \sqrt{\hat{V} [\hat{S} (14)]} \\ 0.69 - 1.96 \sqrt{0.011} < S (14) < 0.69 + 1.96 \sqrt{0.011} \\ 0.48 < S (14) < 0.90. \end{matrix}$

Using this confidence interval procedure for all values of t, Figure 6.4 shows the 95% confidence bands for the survivor function. These confidence intervals have also been cut off after [latex]t = 35[/latex] because the last observation corresponds to a right-censored individual. The bounds are particularly wide because there are only [latex]r = 9[/latex] observed failure times.

Figure 6.4: Confidence bands for the product–limit estimate for the 6–MP treatment group.

Long Description for Figure 6.4

The horizontal axis t ranges from 0 to 35 in increments of 5 units. The vertical axis S of t ranges from 0.0 to 1.0 in increments of 0.2 units. The downward step function with 8 steps decreases from 1.0 to 0.4, whilst the t increases from 0 to 35. The first step is from t equals 0 to 5, and the last step is from t equals 23 to 35, which are the longest steps. The vertical hash marks are placed on the Kaplan Meier estimate at t equals 9, 11, 17, 19, 20, 25, 32, and 34. One band with seven steps lies above the survivor function, with S of t decreases from 1.0 to 0.7 as t increases from 5 to 23 and then maintains a value of 0.7 for the remaining t values. Another band with seven steps lies below the survivor function, and S of t decreases progressively from 0.7 to 0.2 as t increases from 5 to 22, and maintains the same 0.2 for the remaining t values. All values are estimated.

The R code to calculate this confidence interval for [latex]S(14)[/latex] and plot confidence bands around the product–limit estimate is given below. Setting the conf.type argument to “plain” in the call to survfit results in the calculations for the 95% confidence interval for [latex]S(14)[/latex] presented here. These are displayed in the two right-hand columns in the call to the summary function. Setting the mark.time argument to TRUE in the call to plot results in hash marks on the estimated survivor function.

6.1.3 Comparing Two Survivor Functions

This subsection introduces a nonparametric statistical test for determining whether samples of lifetimes from two populations arose from the same probability distribution. This test is nonparametric in the sense that it places no assumptions on the lifetime distribution of either population. The log-rank test (also known as the Mantel–Cox test, named after American biostatistician Nathan Mantel and British statistician David Cox or the Mantel–Haenszel test, named after American epidemiologist William Haenszel) is a nonparametric statistical test that can be used to test the equality of two survivor functions based on two randomly right-censored data sets collected from the two populations.

The null and alternative hypotheses for the log-rank test are

$\begin{array}{l} H_{0} : & S_{1} (t) = S_{2} (t) \\ H_{1} : & S_{1} (t) \neq S_{2} (t), \end{array}$

where [latex]S_1(t)[/latex] is the survivor function of the lifetimes of items from population 1 and [latex]S_2(t)[/latex] is the survivor function of the lifetimes of items from population 2. A randomly right-censored data set is collected from each population. The notation established below is similar to that used in the Kaplan–Meier product–limit estimator. Let [latex]y_1 < y_2 < \cdots < y_k[/latex] be the observed failure times in the combined data set. Let

[latex]n_{1j}[/latex] be the number of items from data set 1 at risk just prior to time y_j,
[latex]n_{2j}[/latex]be the number of items from data set 2 at risk just prior to time y_j,
[latex]n_j = n_{1j} + n_{2j}[/latex],
[latex]d_{1j}[/latex] be the number of items from data set 1 that fail at time y_j,
[latex]d_{2j}[/latex] be the number of items from data set 2 that fail at time y_j,
[latex]d_j = d_{1j} + d_{2j}[/latex],

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].

Just before time y_j, there are n_j items in the combined sample that are at risk and subject to potential failure, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Of the n_j items at risk just before time y_j, there are [latex]n_{1j}[/latex] items from population 1 and [latex]n_{2j}[/latex] items from population 2 that are at risk, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Under H₀, each of the n_j items at risk has an identical conditional time to failure (conditioned on survival to time y_j), for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Under H₀, the random number of failures from population 1 at time y_j, [latex]d_{1j}[/latex], is equivalent to sampling d_j items without replacement from n_j items, [latex]n_{1j}[/latex] of which are type 1 and [latex]n_j - n_{1j}[/latex] of which are type 2. Thus, [latex]d_{1j}[/latex] has the hypergeometric distribution under H₀ with parameters n_j, [latex]n_{1j}[/latex], and d_j, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].

The population mean of the hypergeometric random variable [latex]d_{1j}[/latex] under H₀ is

$\begin{array}{l} E [d_{1 j}] = \frac{d_{j} n_{1 j}}{n_{j}} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. The population variance of [latex]d_{1j}[/latex] under H₀ is

$\begin{array}{l} V [d_{1 j}] = \frac{d_{j} (n_{1 j} / n_{j}) (1 - n_{1 j} / n_{j}) (n_{j} - d_{j})}{n_{j} - 1} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. So the random variables [latex]d_{11}, \, d_{12}, \, \ldots , \, d_{1k}[/latex] are marginally hypergeometric with population means and variances given above. Standardizing and summing, the log-rank test statistic

$\begin{array}{l} Z = \frac{\sum_{j = 1}^{k} (d_{1 j} - E [d_{1 j}])}{\sqrt{\sum_{j = 1}^{k} V [d_{1 j}]}} \end{array}$

is asymptotically standard normal in k under H₀. Large and small values of the test statistic Z correspond to departures from H₀.

Example 6.6 Perform a log-rank test to compare the survivor functions of the remission times in the treatment and control groups in the 6–MP clinical trial data from Example 5.6.

Recall from Example 5.6 that the remission times (in weeks) for the treatment group (population 1) are

$\begin{array}{l} 6 6 6 6^{*} 7 9^{*} 10 10^{*} 11^{*} 13 16 \\ 17^{*} 19^{*} 20^{*} 22 23 25^{*} 32^{*} 32^{*} 34^{*} 35^{*} \end{array}$

and the remission times for the control group (population 2) are

$\begin{array}{l} 1 1 2 2 3 4 4 5 5 8 8 \\ 8 8 11 11 12 12 15 17 22 23. \end{array}$

The estimated survivor functions for the control and treatment groups are displayed in Figure 6.5. The use of 6–MP appears to be effective in prolonging remission times, but is the difference between the two survivor functions statistically significant? The log-rank test will answer this question.

Figure 6.5: Estimated survivor functions for the 6–MP control and treatment and groups.

Long Description for Figure 6.5

The horizontal axis t ranges from 0 to 35 in increments of 5 units. The vertical axis S of t ranges from 0.0 to 1.0 in increments of 0.2 units. The downward step function Control with 12 steps decreases rapidly from 1.0 to 0.4, whilst the t increases from 0 to 23. All are small steps and the long step ranges from t equals 17 to 23. Another downward step function treatment with 8 steps decreases from 1.0 to 0.4 as t increases from 0 to 35. The first step from t equals 0 to 5, the sixth step from t equals 15 to 22, and the last step from t equals 23 to 35 are the longest steps. The vertical hash marks are placed on the Kaplan Meier estimate at t equals 9, 11, 17, 19, 20, 25, 32, and 34. All values are estimated.

The [latex]k = 17[/latex] distinct observed failure times [latex]y_1 < y_2 < \cdots < y_{17}[/latex] in the combined sample are given in the second column of Table 6.3. The next three columns give the number of patients at risk just prior to time y_j in the combined data set (n_j), the number of patients at risk just prior to time y_j from population 1 [latex](n_{1j})[/latex], and number of patients at risk just prior to time y_j from population 2 [latex](n_{2j})[/latex]. The final three columns give the number of overall observed remission times at time y_j in the combined data set (d_j), the number of observed remission times at time y_j from population 1 [latex](d_{1j})[/latex], and the number of observed remission times at time y_j from population 2 [latex](d_{2j})[/latex].

Table 6.3: Data for calculating the log-rank test statistic.
j	y_j	n_j	$n_{1 j}$	$n_{2 j}$	d_j	$d_{1 j}$	$d_{2 j}$
1	1	42	21	21	2	0	2
2	2	40	21	19	2	0	2
3	3	38	21	17	1	0	1
4	4	37	21	16	2	0	2
5	5	35	21	14	2	0	2
6	6	33	21	12	3	3	0
7	7	29	17	12	1	1	0
8	8	28	16	12	4	0	4
9	10	23	15	8	1	1	0
10	11	21	13	8	2	0	2
11	12	18	12	6	2	0	2
12	13	16	12	4	1	1	0
13	15	15	11	4	1	0	1
14	16	14	11	3	1	1	0
15	17	13	10	3	1	0	1
16	22	9	7	2	2	1	1
17	23	7	6	1	2	1	1

The null and alternative hypotheses for the test are

$\begin{array}{l} H_{0} : & S_{1} (t) = S_{2} (t) \\ H_{1} : & S_{1} (t) \neq S_{2} (t), \end{array}$

and the test statistic is

$\begin{array}{l} Z = \frac{\sum_{j = 1}^{17} (d_{1 j} - E [d_{1 j}])}{\sqrt{\sum_{j = 1}^{17} V [d_{1 j}]}} = - 4.1 . \end{array}$

This test statistic is negative because the observed [latex]d_{1j}[/latex] values are smaller than their expected values. Fewer remissions occur in sample 1 (those patients treated with 6–MP) than expected if the remission time distributions in the two populations were identical. Since the test statistic is 4.1 standard deviation units from its population mean under H₀, we expect a small p-value, and a rejection of the null hypothesis H₀. The p-value is

$\begin{array}{l} p = 2 \cdot P (Z < - 4.1) = 0.00004, \end{array}$

so the conclusion is to reject H₀. There is statistical evidence that the survivor functions for the control and treatment groups differ. Figure 6.5 shows that the patients taking 6–MP have longer remission times.

Here are three final observations on the log-rank test. First, the test has been extended from testing the equality of two populations to testing the equality of several populations. Second, the Peto log-rank test statistic (named after British statistician Julian Peto) gives differing weights to the observed failure times. Third, there are several competitors to the log-rank test which should be considered when using this test.

6.2 Competing Risks

In competing risks models, several causes of failure compete for the lifetime of an item. These models are also useful for analyzing the relationships between the causes of failure. In addition, competing risks models are one way of combining several distributions to achieve a lifetime distribution with, for example, a bathtub-shaped hazard function.

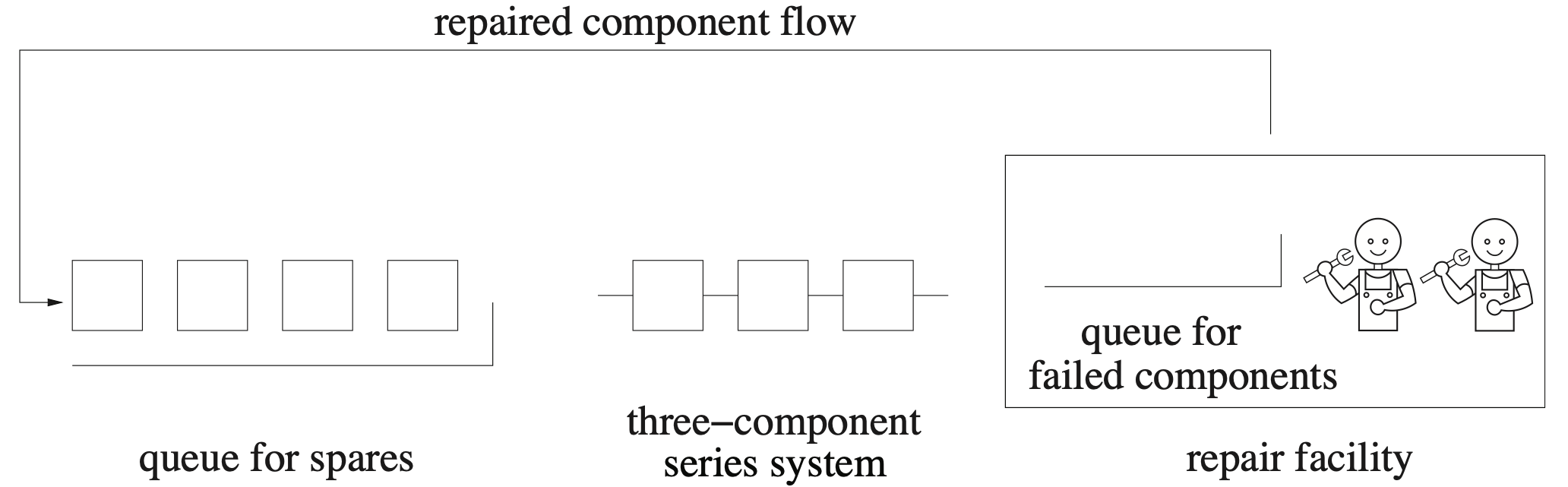
In some situations, causes of failure can be grouped into k classes. An electrical engineer, for instance, might use failure by short and failure by open as a two-element competing risks model for the lifetime of a diode. Likewise, an actuary might use heart disease, cancer, accidents, and all other causes as a four-element competing risks model for human lifetimes. In competing risks analysis, an item is assumed to be subject to k competing risks (or causes) denoted by [latex]C_1, \, C_2, \, \ldots, \, C_k[/latex]. Competing risks, often called multiple decrements by actuaries, can be viewed as a series system of components. Each risk can be thought of as a component in a series system in which system failure occurs when any component fails. Analyzing problems by competing risks might require the modeler to include an “all other risks” classification in order to study the effect of reduction or elimination of one risk. The origins of competing risks theory can be traced to a study by Daniel Bernoulli in the 1700s concerning the impact of eliminating smallpox on mortality for various age groups.

A second and equally appealing use of competing risks models is that they can be used to combine component distributions to form more complicated models. Although a distribution with a bathtub-shaped hazard function is often cited as an appropriate lifetime model, none of the five most popular lifetime distribution models (exponential, Weibull, gamma, log normal, and log logistic) can achieve this shape. Competing risks models are one way of combining several distributions to achieve a bathtub-shaped lifetime distribution. As shown in Figure 6.6, if a DFR Weibull distribution is used to model manufacturing defect failures and an IFR Weibull distribution is used to model wear-out failures, then a competing risks model with [latex]k = 2[/latex] risks yields a bathtub-shaped hazard function because the hazard functions are summed. We will formally develop this result later in this section.

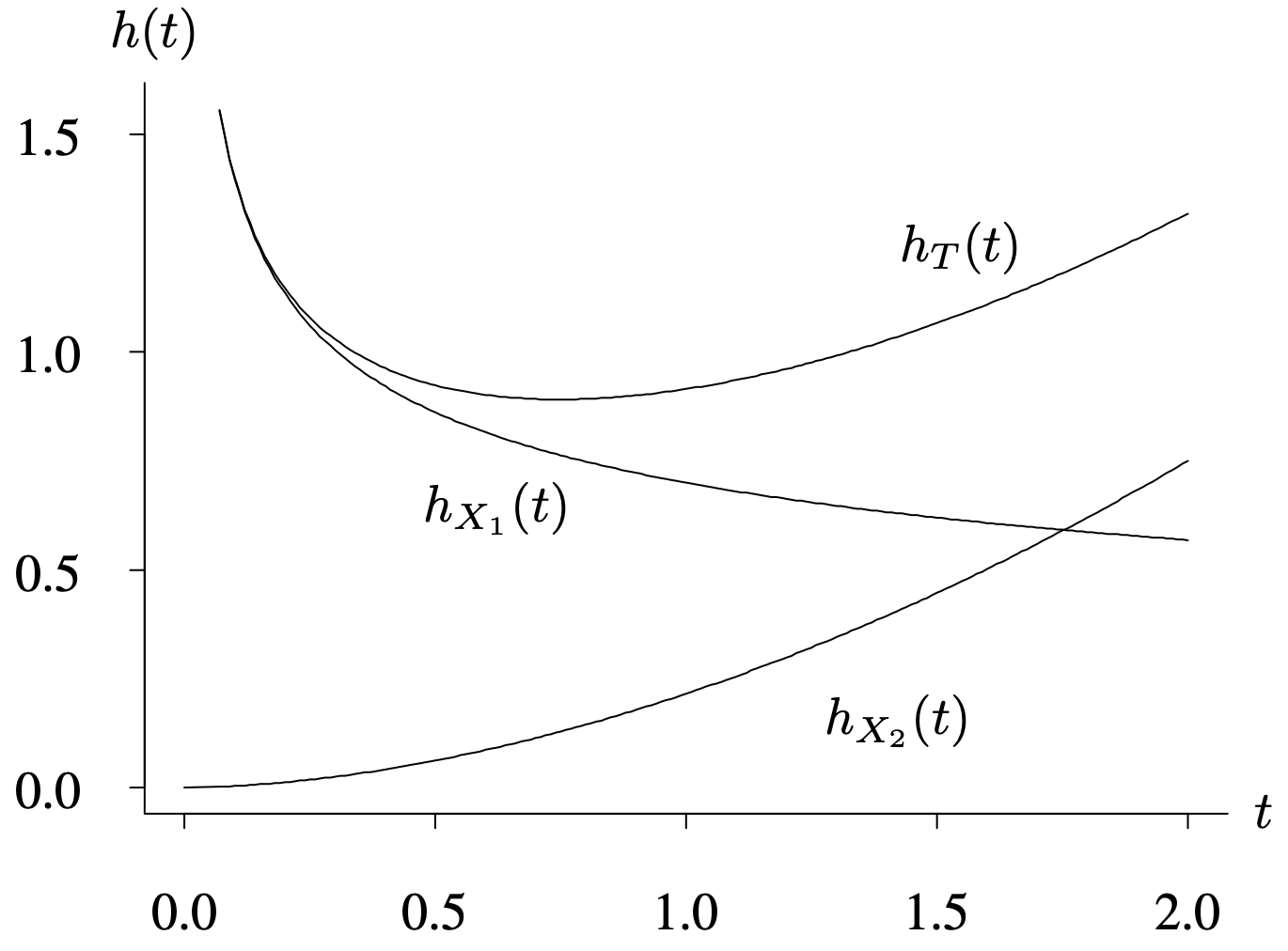
A graph of the three hazard functions on a coordinate plane. — Figure 6.6: Hazard functions for a competing risks model.

Long Description for Figure 6.6

The horizontal axis t ranges from 0.0 to 2.0 in increments of 0.5 units. The vertical axis h of t ranges from 0.0 to 1.5 in increments of 0.5 units. The function h subscript uppercase T of lowercase t is a concave curve, which decreases from (0.0, 1.5), reaches a low point at (0.6, 1.1), and increases to (2.0, 1.3). The concave curve of function h subscript X 1 decreases from (0.0, 1.5) to (2.0, 0.5). The concave curve of function h subscript X 2 of t increases from (0.0, 0.0) to (2.0, 0.75). All data are estimated.

6.2.1 Net Lifetimes

Competing risks theory is complicated by the existence of net and crude lifetimes. When working with net lifetimes or net probabilities, the causes [latex]C_1, \, C_2, \, \ldots, \, C_k[/latex] are viewed individually; that is, risk C_j, [latex]j = 1, \, 2, \, \ldots, \, k[/latex], is analyzed as if it is the only risk acting on the population. When working with crude lifetimes or crude probabilities, the lifetimes are considered in the presence of all other risks. The random variables associated with net lifetimes are defined next.

Unless all risks except j are eliminated, X_j is not necessarily observed. In this sense, each net lifetime is a potential lifetime that is observed with certainty only if all the other [latex]k-1[/latex] risks are eliminated. The observed lifetime of an item, T, is the minimum of [latex]X_1, \, X_2, \, \ldots, \, X_k[/latex]. When the net lives are independent random variables, the hazard function for the observed time to failure is [latex]h_T (t) = \sum_{{j\,=\,1}}^k h_{X_j} (t)[/latex], because [latex]S_T (t) = \prod_{{j\,=\,1}}^k S_{X_j} (t)[/latex] for a series system of k independent components, [latex]H_{T}(t) = -\ln \, S_{T}(t)[/latex], and [latex]h_{T}(t) = H_{T}^\prime (t)[/latex]:

$\begin{array}{l} h_{T} (t) & = \frac{d}{d t} H_{T} (t) \\ = \frac{d}{d t} [- \ln S_{T} (t)] \\ = \frac{d}{d t} [- \ln (\prod_{j = 1}^{k} S_{X_{j}} (t))] \\ = \frac{d}{d t} [\sum_{j = 1}^{k} - \ln S_{X_{j}} (t)] \\ = \frac{d}{d t} [\sum_{j = 1}^{k} H_{X_{j}} (t)] \\ = \sum_{j = 1}^{k} \frac{d}{d t} H_{X_{j}} (t) \\ = \sum_{j = 1}^{k} h_{X_{j}} (t) t \geq 0. \end{array}$

The net probability of failure in the time interval [latex][a, \, b)[/latex] from risk j, denoted by [latex]q_j (a, \, b)[/latex], is the probability of failure in [latex][a, \, b)[/latex] from risk j if risk j is the only risk present, conditioned on survival to time a. So

$\begin{array}{l} q_{j} (a, b) & = P (a \leq X_{j} < b | X_{j} \geq a) \\ = 1 - P (X_{j} \geq b | X_{j} \geq a) \\ = 1 - \frac{P (X_{j} \geq b)}{P (X_{j} \geq a)} \\ = 1 - \frac{S_{X_{j}} (b)}{S_{X_{j}} (a)} \\ = 1 - \frac{e^{- H_{X_{j}} (b)}}{e^{- H_{X_{j}} (a)}} \\ = 1 - e^{- (H_{X_{j}} (b) - H_{X_{j}} (a))} \\ = 1 - e^{- \int_{a}^{b} h_{X_{j}} (t) d t} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].

6.2.2 Crude Lifetimes

Crude lifetimes are more difficult to work with than net lifetimes because they consider each of the causes of failure in the presence of all other causes of failure. Crude lifetimes are observed when lifetime data values are collected in a competing risks model in which all causes of failure are acting simultaneously in the population.

The crude probability of failure in the time interval [latex][a, \, b)[/latex] from cause j, denoted by [latex]Q_j (a, \, b)[/latex], is the probability of failure in [latex][a, \, b)[/latex] from risk j in the presence of all other risks, conditioned on survival of all risks to time a. A well-known result in competing risks theory gives this probability as

$\begin{array}{l} Q_{j} (a, b) & = P (a \leq X_{j} < b, X_{j} < X_{i} for all i \neq j | T \geq a) \\ = \int_{a}^{b} h_{X_{j}} (x) e^{- \int_{a}^{x} h_{T} (t) d t} d x \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Rather than isolating individual risks, as in the case of net lifetimes, this quantity considers risk j as it works in the presence of the [latex]k - 1[/latex] other risks. The probability of failure due to risk j is defined by [latex]\pi_j = P(X_j = T)[/latex], for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Since failure will occur from one of the causes,

$\begin{array}{l} \sum_{j = 1}^{k} π_{j} = 1. \end{array}$

A simple example to illustrate some of the concepts in competing risks is given next before the general theory is developed.

Example 6.7 Consider an item that is subject to [latex]k= 2[/latex] causes of failure. Let the random variables X₁ and X₂ be the net lives for causes C₁ and C₂. If the item under consideration is a cell phone, for instance, cause 1 might be dropping the cell phone and cause 2 might be all other causes (for example, battery or display failure). In this case, X₁ is the life of the cell phone if the only way it can fail is by being dropped. The second net life, X₂, is the lifetime of the cell phone if it is bolted to a desk and cannot be dropped. The first crude life, Y₁, is the failure time of a cell phone that failed due to being dropped in the presence of the second cause of failure. Likewise, Y₂ is the lifetime of a cell phone that failed by some mode other than being dropped, but was not bolted to a desk to avoid its being dropped. Let the observed lifetime, T, be the minimum of X₁ and X₂. Also, assume that X₁ and X₂ are independent and have exponential distributions with population means 1 and [latex]1/2[/latex], respectively. Thus,

$\begin{array}{l} S_{X_{1}} (t) = e^{- t} f_{X_{1}} (t) = e^{- t} h_{X_{1}} (t) = 1 \end{array}$

and

$\begin{array}{l} S_{X_{2}} (t) = e^{- 2 t} f_{X_{2}} (t) = 2 e^{- 2 t} h_{X_{2}} (t) = 2 \end{array}$

for [latex]t \ge 0[/latex]. The net probabilities of failure in the interval [latex][a,b)[/latex] are

$\begin{array}{l} q_{1} (a, b) = 1 - e^{- \int_{a}^{b} 1 d t} = 1 - e^{- (b - a)} \end{array}$

and

$\begin{array}{l} q_{2} (a, b) = 1 - e^{- \int_{a}^{b} 2 d t} = 1 - e^{- 2 (b - a)} \end{array}$

for [latex]0 < a < b[/latex]. The crude probability of failure due to the first risk in the interval [latex][a, \, b)[/latex], [latex]Q_1 (a, \, b)[/latex], is the integral of the joint probability density function of X₁ and X₂ over the shaded area in Figure 6.7 (illustrated for [latex]a = 0.5[/latex] and [latex]b = 1.2[/latex]), divided by the integral of the joint probability density function of X₁ and X₂ over the area to the northeast of the point [latex](a, \, a)[/latex]. Thus,

$\begin{array}{l} Q_{1} (a, b) & = P (a \leq X_{1} < b and X_{1} < X_{2} | T \geq a) \\ = \frac{P (a \leq X_{1} < b and X_{1} < X_{2})}{P (X_{1} \geq a, X_{2} \geq a)} \\ = \frac{\int_{a}^{b} \int_{x_{1}}^{\infty} e^{- w_{1}} 2 e^{- 2 w_{2}} d w_{2} d w_{1}}{\int_{a}^{\infty} \int_{a}^{\infty} e^{- w_{1}} 2 e^{- 2 w_{2}} d w_{2} d w_{1}} \\ = \frac{1}{3} [1 - e^{- 3 (b - a)}] \end{array}$

Figure 6.7: Numerator integration region for [latex]Q_1(a, \, b)[/latex] for [latex]a = 0.5[/latex] and [latex]b = 1.2[/latex].

for [latex]0 < a < b[/latex]. Similarly,

$\begin{array}{l} Q_{2} (a, b) = \frac{2}{3} [1 - e^{- 3 (b - a)}] \end{array}$

for [latex]0 < a < b[/latex]. The [latex]Q_j (a, \, b)[/latex] expressions have been determined by using their definitions. Alternatively, the formula given earlier,

$\begin{array}{l} Q_{j} (a, b) = \int_{a}^{b} h_{X_{j}} (x) e^{- \int_{a}^{x} h_{T} (t) d t} d x, \end{array}$

for [latex]j = 1, \, 2[/latex], can be used to determine these quantities. For this particular example,

$\begin{array}{l} Q_{1} (a, b) = \int_{a}^{b} e^{- \int_{a}^{x} 3 d t} d x = \frac{1}{3} [1 - e^{- 3 (b - a)}] \end{array}$

and

$\begin{array}{l} Q_{2} (a, b) = \int_{a}^{b} 2 e^{- \int_{a}^{x} 3 d t} d x = \frac{2}{3} [1 - e^{- 3 (b - a)}] \end{array}$

for [latex]0 < a < b[/latex] because [latex]h_T(t) = h_{X_1}(t) + h_{X_2}(t) = 1 + 2 = 3[/latex] for [latex]t \ge 0[/latex]. The probability of failure due to risk 1, π₁, can be found by integrating the joint density of the net lives [latex]f(x_1, \, x_2)[/latex] over the area [latex]X_1 < X_2[/latex] or, equivalently, using [latex]a= 0[/latex] and [latex]b= \infty[/latex] as arguments in [latex]Q_1 (a, \, b)[/latex], yielding [latex]\pi_1= 1 / 3[/latex]. Similarly, [latex]\pi_2= 2 / 3[/latex].

The focus now shifts to the determination of the distribution of the crude lives, Y₁ and Y₂. What is the survivor function for items that fail from one risk in the presence of the other risk? This survivor function is important because data collected in competing risks models often come in pairs: the cause of failure and the time of failure. The observed time of failure is typically a crude lifetime because it is observed in the presence of the other cause(s). The survivor function for the first crude lifetime, [latex]S_{Y_1}(y_1 )[/latex] corresponds to a cell phone that fails by being dropped in the presence of risk C₂. If an analyst had a large data set of cell phone failure times for those cell phones that failed by being dropped, an empirical survivor function will converge to [latex]S_{Y_1}(y_1 )[/latex] as the sample size increases. The survivor function for Y₁ is

$\begin{array}{l} S_{Y_{1}} (y_{1}) & = P (T \geq y_{1} | X_{1} = T) \\ = \frac{P (T \geq y_{1}, X_{1} = T)}{π_{1}} \\ = \frac{\int_{y_{1}}^{\infty} \int_{x_{1}}^{\infty} e^{- w_{1}} 2 e^{- 2 w_{2}} d w_{2} d w_{1}}{1 / 3} \\ = e^{- 3 y_{1}} y_{1} \geq 0. \end{array}$

Similarly,

$\begin{array}{l} S_{Y_{2}} (y_{2}) = e^{- 3 y_{2}} y_{2} \geq 0. \end{array}$

This surprising result, that both Y₁ and Y₂ have the same exponential distribution with population mean [latex]1/3[/latex], can be attributed to the definition of a crude lifetime. Since the two crude lifetimes are the minimum of two exponential random variables (the exponential net lifetimes), each will have an exponential distribution with a parameter being the sum of the rates. The crude lifetime Y₁, for example, consists of only those exponential(1) random variables that are smaller than another independent exponential(2) random variable. Likewise, the crude lifetime Y₂ consists of only those exponential(2) random variables that are smaller than another independent exponential(1) random variable. Theorem 4.4 provides the basis for the fact that the minimum of independent exponential random variables is also exponentially distributed.

As a result, there are two valid ways to generate a random lifetime T for use in Monte Carlo simulation. First, taking the net lifetime perspective, generate an exponential(1) random variate and an exponential(2) random variate and choose the minimum as T. Second, taking the crude lifetime perspective, generate an exponential(3) random variate T and indicate this is failure from risk 1 with probability [latex]1/3[/latex] and failure from risk 2 with probability [latex]2/3[/latex].

6.2.3 General Case

A general theory for competing risks is now developed based on the definitions for net and crude lifetimes given previously. Let [latex]X_1, \, X_2, \, \ldots, \, X_k[/latex] be the k continuous net lives and [latex]{T = \min \{X_1 , \, X_2, \, \ldots, \, X_k \}}[/latex] be the observed failure time of the item. The X_j‘s are not necessarily independent as they were in Example 6.7. Letting the net lives have joint probability density function [latex]f(x_1 , \, x_2, \, \ldots, \, x_k )[/latex], the joint survivor function is

$\begin{array}{l} S (x_{1}, x_{2}, \dots, x_{k}) & = P (X_{1} \geq x_{1}, X_{2} \geq x_{2}, \dots, X_{k} \geq x_{k}) \\ = \int_{x_{k}}^{\infty} \dots \int_{x_{2}}^{\infty} \int_{x_{1}}^{\infty} f (t_{1}, t_{2}, \dots, t_{k}) d t_{1} d t_{2} \dots d t_{k} \end{array}$

and the marginal net survival function is

$\begin{array}{l} S_{X_{j}} (x_{j}) = P (X_{j} \geq x_{j}) = S (0, \dots, x_{j}, \dots, 0) \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. The survivor function for the observed lifetime T is

$\begin{array}{l} S_{T} (t) = P (T \geq t) = S (t, t, \dots, t) . \end{array}$

The probability of failure from risk j can be determined from the joint survivor function because

$\begin{array}{l} - \frac{\partial}{\partial x_{j}} S (x_{1}, \dots, x_{j}, \dots, x_{k}) = lim_{Δ x \to 0} \frac{S (x_{1}, \dots, x_{j}, \dots, x_{k}) - S (x_{1}, \dots, x_{j} + Δ x, \dots, x_{k})}{Δ x} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex] by the definition of the derivative. Thus,

$\begin{array}{l} π_{j} = \int_{0}^{\infty} - {[\frac{\partial}{\partial x_{j}} S (x_{1}, \dots, x_{j}, \dots, x_{k})]}_{x_{1} = x_{2} = \dots = x_{k} = x} d x \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. To derive a survivor function for the crude lifetimes, let the random variable J be the index of the cause of failure so that

$\begin{array}{l} P (T \geq t, J = j) & = P (X_{j} \geq t, X_{j} < X_{i} for all i \neq j) \\ = \int_{t}^{\infty} [\int_{x_{j}}^{\infty} \dots \int_{x_{j}}^{\infty} \int_{x_{j}}^{\infty} f (x_{1}, x_{2}, \dots, x_{k}) \prod_{i \neq j} d x_{i}] d x_{j} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex], where the survivor function for T is obtained by conditioning:

$\begin{array}{l} S_{T} (t) & = P (T \geq t) \\ = \sum_{j = 1}^{k} P (T \geq t | J = j) P (J = j) \\ = \sum_{j = 1}^{k} P (T \geq t, J = j) . \end{array}$

When [latex]t = 0[/latex], each term in the last summation is one of the π_j‘s because

$\begin{array}{l} π_{j} = P (J = j) = P (T \geq 0, J = j) \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex]. Thus, the distribution of the jth crude life, Y_j, is the distribution of T conditioned on [latex]J = j[/latex]:

$\begin{array}{l} S_{Y_{j}} (y_{j}) = P (T \geq y_{j} | J = j) = \frac{P (T \geq y_{j}, J = j)}{P (J = j)} \end{array}$

for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].

Example 6.8 The competing risks model from Example 6.7, which considered two independent, exponentially distributed risks, is used to illustrate the use of the formulas developed thus far. As before, let the net lives have marginal survivor functions

$\begin{array}{l} S_{X_{1}} (t) = e^{- t} S_{X_{2}} (t) = e^{- 2 t} \end{array}$

for [latex]t \ge 0[/latex]. Since the risks are independent, the joint survivor function is

$\begin{array}{l} S (x_{1}, x_{2}) = S_{X_{1}} (x_{1}) \cdot S_{X_{2}} (x_{2}) = e^{- x_{1} - 2 x_{2}} x_{1} \geq 0, x_{2} \geq 0. \end{array}$

The probability of failure from the first risk is

$\begin{array}{l} π_{1} & = \int_{0}^{\infty} - {[\frac{\partial}{\partial x_{1}} S (x_{1}, x_{2})]}_{x_{1} = x_{2} = x} d x \\ = \int_{0}^{\infty} - [- e^{- x_{1} - 2 x_{2}}]_{x_{1} = x_{2} = x} d x \\ = \int_{0}^{\infty} e^{- 3 x} d x \\ = \frac{1}{3} . \end{array}$

Since [latex]\pi_2 = 1 - \pi_1[/latex],

$\begin{array}{l} π_{2} = \frac{2}{3} . \end{array}$

The probability of survival to time t and risk 1 being the cause of failure is

$\begin{array}{l} P (T \geq t, J = 1) & = P (X_{1} \geq t, X_{1} < X_{2}) \\ = \int_{t}^{\infty} [\int_{x_{1}}^{\infty} f (x_{1}, x_{2}) d x_{2}] d x_{1} \\ = \int_{t}^{\infty} \int_{x_{1}}^{\infty} 2 e^{- x_{1} - 2 x_{2}} d x_{2} d x_{1} \\ = \int_{t}^{\infty} e^{- 3 x_{1}} d x_{1} \\ = \frac{1}{3} e^{- 3 t} t \geq 0. \end{array}$

Similarly,

$\begin{array}{l} P (T \geq t, J = 2) = \frac{2}{3} e^{- 3 t} t \geq 0. \end{array}$

Thus, the survival function for the first crude lifetime is

$\begin{array}{l} S_{Y_{1}} (y_{1}) = \frac{P (T \geq y_{1}, J = 1)}{P (J = 1)} = e^{- 3 y_{1}} y_{1} \geq 0 \end{array}$

and the survival function for the second crude lifetime is

$\begin{array}{l} S_{Y_{2}} (y_{2}) = \frac{P (T \geq y_{2}, J = 2)}{P (J = 2)} = e^{- 3 y_{2}} y_{2} \geq 0. \end{array}$

These results are identical to those derived from first principles in the previous example. Both crude lifetimes have an exponential(3) distribution.

To this point, it has been shown how the distribution of the net lives [latex]X_1, \, X_2, \, \ldots, \, X_k[/latex] determines the distribution of the crude lives [latex]Y_1, \, Y_2, \, \ldots, \, Y_k[/latex]. Net lives can be interpreted as potential lifetimes, while crude lives are the observed lifetimes. When lifetime data for the known cause of failure are collected, the observed values are Y_j‘s. An important question is whether the distribution of each Y_j contains enough information to determine the distribution of the X_j‘s. In general, the answer is no, but under the assumption of independence of the net lives, the answer is yes. The following discussion considers results under the assumption of independent net lives. This independence can often be attained by grouping the k risks so that dependencies occur within, but not between, risks.

The proof of this result is given in a reference listed in the preface. This result is useful for determining the effect of removing one or more risks when the distributions of the crude lives are determined from a data set, as illustrated in the next example.

Example 6.9 Consider again the competing risks model from Example 6.8 in which the [latex]k = 2[/latex] risks were assumed to be independent. If a large number of failure times are collected, and the cause of failure is identifiable (that is, both the failure time and the index of the risk that caused failure are known), it might be possible to determine the distribution of the two crude lifetimes. If both are well fitted with an exponential distribution with failure rate [latex]\lambda = 3[/latex], and approximately one-third of the failures are from cause 1, then

$\begin{array}{l} π_{1} = P (J = 1) = \frac{1}{3} π_{2} = P (J = 2) = \frac{2}{3} \end{array}$

and

$\begin{array}{l} S_{Y_{1}} (t) = e^{- 3 t} S_{Y_{2}} (t) = e^{- 3 t} \end{array}$

for [latex]t \ge 0[/latex]. Therefore, by Theorem 6.1 the hazard functions for the net lives are

$\begin{array}{l} h_{X_{1}} (t) = \frac{\frac{1}{3} \cdot 3 e^{- 3 t}}{\frac{1}{3} e^{- 3 t} + \frac{2}{3} e^{- 3 t}} = 1 t \geq 0 \end{array}$

and

$\begin{array}{l} h_{X_{2}} (t) = \frac{\frac{2}{3} \cdot 3 e^{- 3 t}}{\frac{1}{3} e^{- 3 t} + \frac{2}{3} e^{- 3 t}} = 2 t \geq 0. \end{array}$

This result is consistent with the previous two examples.

The previous three examples have considered competing risks models with [latex]k = 2[/latex] risks and exponentially distributed net and crude lifetimes. This section concludes with an example of a competing risks model with [latex]k = 3[/latex] risks and non-exponential net lifetimes.

Example 6.10 An item is subject to [latex]k = 3[/latex] competing risks C₁, C₂, and C₃ with the three associated independent net lifetimes: [latex]X_1 \sim \hbox{Weibull}(1, \, 2)[/latex], [latex]X_2 \sim \hbox{exponential}(1)[/latex], and [latex]X_3 \sim \hbox{Weibull}(1, \, 3)[/latex].

What is the population mean time to failure of the item?
If one of the risks could be eliminated, the elimination of which risk results in the greatest increase in the population mean time to failure of the item?

The hazard function associated with a Weibull([latex]\lambda, \, \kappa[/latex]) random variable is
$\begin{array}{l} h (t) = κ λ^{κ} t^{κ - 1} t \geq 0. \end{array}$

The hazard functions for the three net lifetimes are

$\begin{array}{l} h_{X_{1}} (t) = 2 t h_{X_{2}} (t) = 1 h_{X_{3}} (t) = 3 t^{2} \end{array}$

for [latex]t \ge 0[/latex]. The hazard function for the time to failure of the item T is the sum of the hazard functions for the three net lifetimes:

$\begin{array}{l} h_{T} (t) = 3 t^{2} + 2 t + 1 t \geq 0. \end{array}$

The associated cumulative hazard function is

$\begin{array}{l} H_{T} (t) & = \int_{0}^{t} h_{T} (τ) d τ \\ = \int_{0}^{t} (3 τ^{2} + 2 τ + 1) d τ \\ = {[τ^{3} + τ^{2} + τ]}_{0}^{t} \\ = t^{3} + t^{2} + t t \geq 0. \end{array}$

The associated survivor function is

$\begin{array}{l} S_{T} (t) = e^{- H_{T} (t)} = e^{- t^{3} - t^{2} - t} t \geq 0. \end{array}$

So the population mean time to failure of the item is

$\begin{array}{l} E [T] = \int_{0}^{\infty} S_{T} (t) d t = \int_{0}^{\infty} e^{- t^{3} - t^{2} - t} d t ≅ 0.4630, \end{array}$

where the integral must be evaluated numerically.
The same procedure given in part (a) can be used to assess the effect of removing risks. The results are given in Table 6.4. Removing risk 2 makes the greatest improvement on the population mean lifetime of the item.

Table 6.4: Mean lifetimes associated with eliminated risks.
Risk eliminated	Risk 1	Risk 2	Risk 3
E[T]	0.5689	0.6637	0.5456

To summarize this section, competing risks models are appropriate when there are k causes of failure and the occurrence of failure due to any risk causes the item to fail. These k risks can be thought of conceptually as a k-component series system. The probabilities of failure from the various causes are denoted by [latex]\pi_1, \, \pi_2, \, \ldots, \, \pi_k[/latex]. The net lifetimes [latex]X_1 , \, X_2, \, \ldots, \, X_k[/latex] occur if only one risk is evident at a time in the population. The crude lifetimes [latex]Y_1, \, Y_2, \, \ldots, \, Y_k[/latex] occur in the presence of all other risks. If the net lives are independent, once the distributions of [latex]Y_1, \, Y_2, \, \ldots, \, Y_k[/latex] and [latex]\pi_1, \, \pi_2, \, \ldots, \, \pi_k[/latex] are determined, the distribution of the net lives [latex]X_1 , \, X_2, \, \ldots, \, X_k[/latex] can be determined.

6.3 Point Processes

So far, the focus has been on a single random variable T, generically referred to as a lifetime, and methods for estimating its probability distribution. In a reliability setting, T might be the lifetime of a light bulb. In a biostatistical setting, T might be the post-surgery remission time for a patient having a particular type of cancer. In an actuarial setting, T might be the time of death for a insured individual having a life insurance policy. In all of these examples, there is only a single random variable T that is of interest.

Occasions arise, however, when there are multiple events of interest. In a reliability setting, the sequence of events might be the repair times for an automobile. In a biostatistical setting, the sequence of events might be the times at which a cortisone injection is administered to a patient. In an actuarial setting, the sequence of events might be the times of insurance claims on an insured dwelling. In all of these examples, the probability mechanism governing the sequence of observations is of interest.

Point process models are often used to describe the probability mechanism governing a series of event times. The three elementary point process models considered in this section are Poisson processes, renewal processes, and nonhomogeneous Poisson processes.

Point process models can be applied to more than just failure times of repairable systems. Point processes have been used to describe arrival times to queues, earthquake times, hurricane landfall times, pothole positions on a highway, and other physical phenomena. They have also been used to describe the occurrence times of sociological events such as crimes, strikes, bankruptcies, and wars.

The examples in this section use reliability jargon, leaving it to the reader to extend the models to other disciplines. The reliability-centric term “failure” is used instead of the more generic term “event” for all of the point processes described in this section. The object of interest will continue to be referred to generically as an “item.”

When the time to repair or replace an item is negligible, point processes are appropriate for modeling the probabilistic mechanism underlying the failure times. This would be the case for an automobile that works without failure for months, and then is in the shop for one hour for a repair in which no mileage is accrued while the maintenance is being performed. These models would not be appropriate, for example, for an aircraft that spends several months having its engine overhauled before being placed back into service if availability is of interest. The down time needs to be explicitly modeled in this case.

A small but important bit of terminology is used to differentiate between nonrepairable items, which were considered in the previous chapters, and repairable items, which are considered here. A nonrepairable item, such as a light bulb, has one failure, and the term burn in is used if its hazard function is decreasing and the term wear out is used if its hazard function is increasing. Figure 6.8 shows hazard functions for an item that undergoes burn in and another that wears out. The × on the time axis denotes a realization of one possible failure time. The lifetimes of nonrepairable items are described by the distribution of a single nonnegative random variable, usually denoted by T.

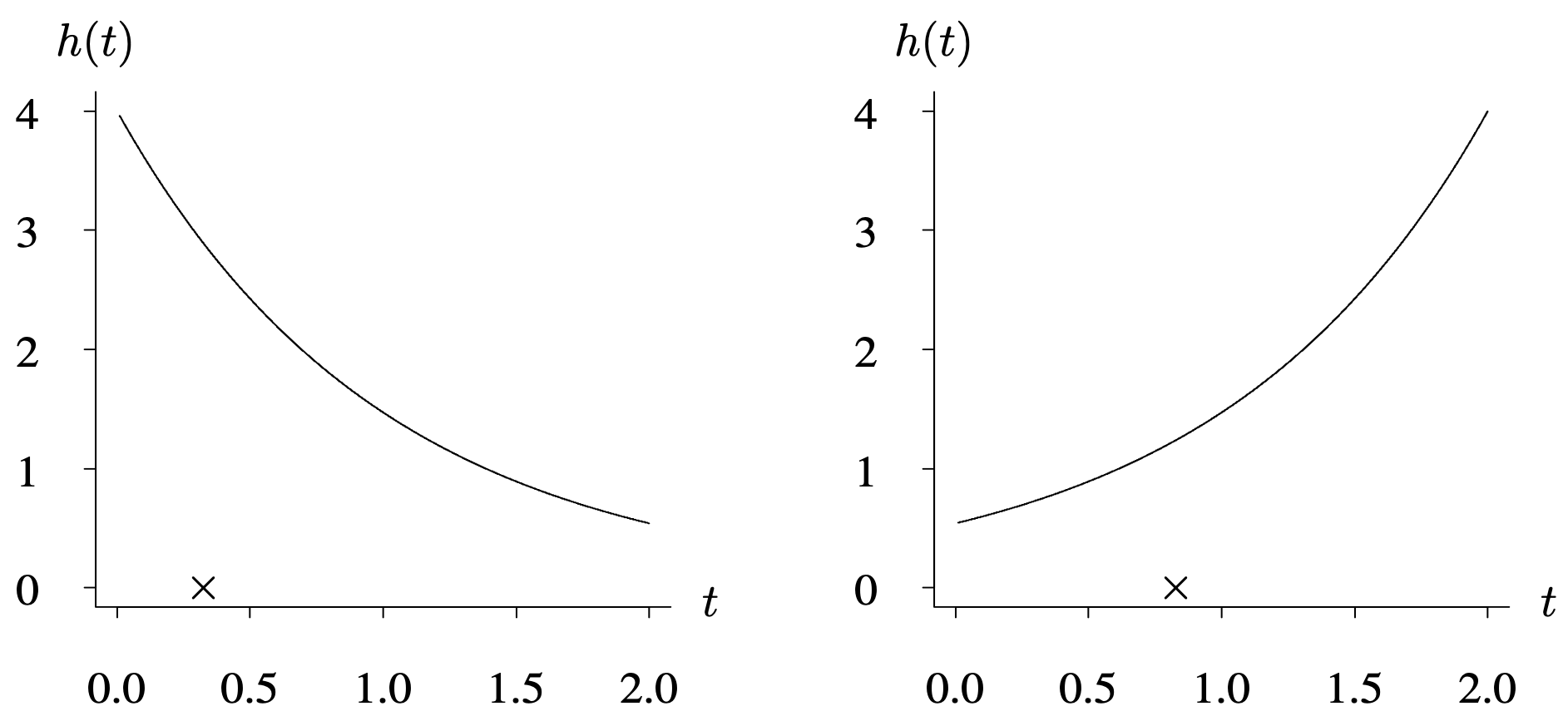
Graphs of the two hazard functions for non repairable items. — Figure 6.8: Hazard functions for nonrepairable items in the DFR and IFR classes.

Long Description for Figure 6.8

In both graphs, the horizontal axis t ranges from 0.0 to 2.0 in increments of 0.5 units. The vertical axis h of t ranges from 0 to 4 in increments of 1 unit. In the first graph, the function decreases from (0.0, 4) through (1, 1.5) to (2.0, 0.8) in a concave curve. The x mark is at (0.3, 0). In the second graph, the function increases from (0, 0.5) through (1.0, 1.5) to (2.0, 4) in a concave curve. The X is plotted at (0.8, 0). All data are estimated.

In contrast, a repairable item, such as an automobile, typically fails at several points in time. In many situations, a nonhomogeneous Poisson process, which is governed by the intensity function [latex]\lambda (t)[/latex] that reflects the rate of occurrence of failures, might be the appropriate probabilistic mechanism for modeling the failure history of the item. The intensity function is analogous to the hazard function in the sense that higher levels of [latex]\lambda (t)[/latex] indicate an increased probability of failure. The term improvement is used if the intensity function is decreasing, and the term deterioration is used if the intensity function is increasing. Figure 6.9 shows intensity functions for an item that improves and another that deteriorates. Each × on the time axis denotes a failure time associated with a realization. The improving item has failures that tend to be less frequent as time passes; the deteriorating item has failures that tend to be more frequent as time passes. The failure times of repairable items are described by the probability mechanism underlying a sequence of random variables, often denoted by [latex]T_1, \, T_2, \, \ldots[/latex]. These terms are summarized in Table 6.5.

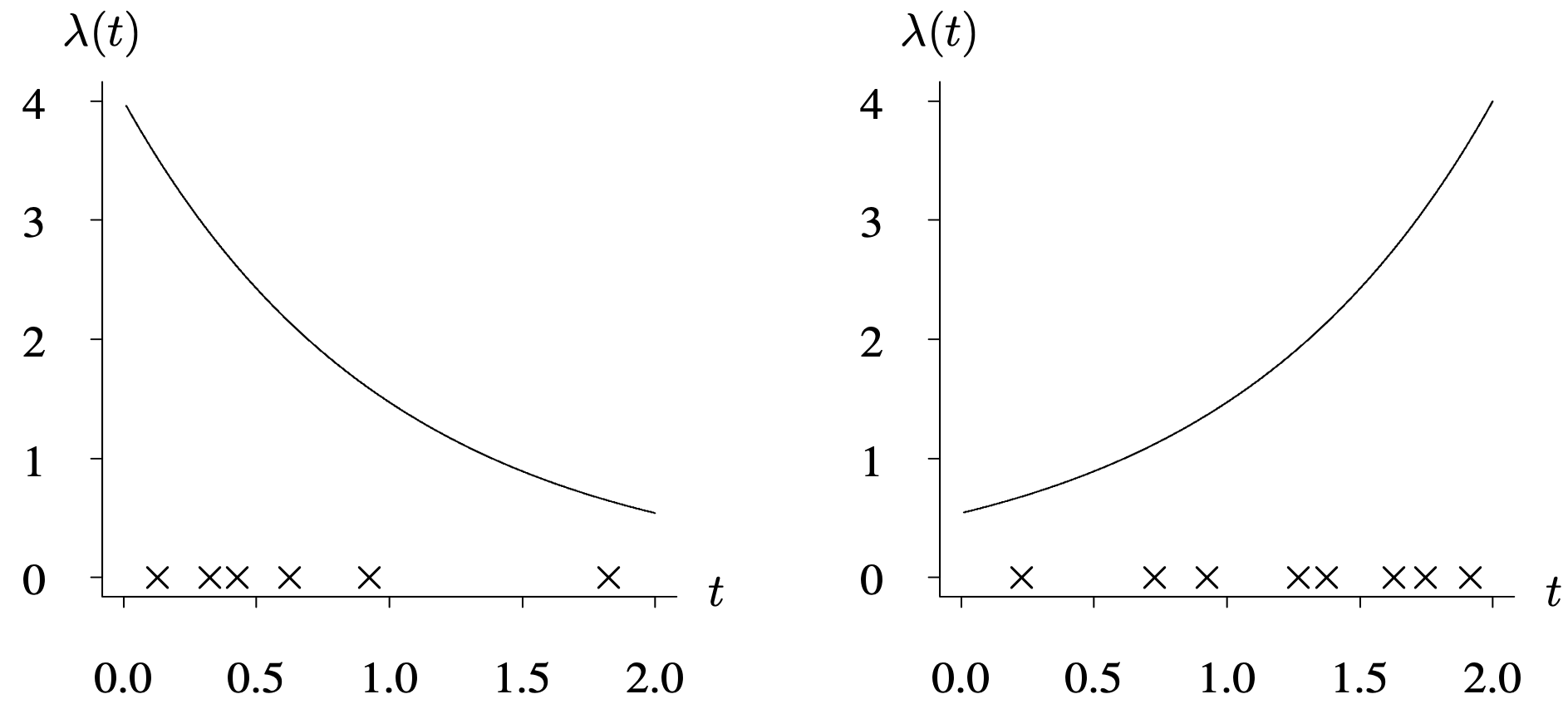
Graphs of the intensity functions for repairable improving and deteriorating items. — Figure 6.9: Intensity functions for a repairable improving and deteriorating items.

Long Description for Figure 6.9

In both graphs, the horizontal axis t ranges from 0.0 to 2.0 in increments of 0.5 units. The vertical axis lambda of t ranges from 0 to 4 in increments of 1 unit. In the first graph, the function decreases from (0.0, 4) through (1, 1.5) to (2.0, 0.8) in a concave curve. The X marks are on the horizontal axis at t values 0.1, 0.3, 0.4, 0.6, 0.9, an 1.8. In the second graph, the function increases from (0, 0.5) through (1.0, 1.5) to (2.0, 4) in a concave curve. The X marks are plotted on the horizontal axis at t values 0.2, 0.7, 0.9, 1.2, 1.3, 1.6, 1.7, and 1.9. All data are estimated.

Table 6.5: Terminology for nonrepairable and repairable items in the reliability setting.
	Nonrepairable	Repairable
Item gets better as time passes	Burn in, [latex]h ^ {\kern 0.04em \prime} (t) \le 0[/latex]	Improving, [latex]\lambda ^ \prime(t) \le 0[/latex]
Item gets worse as time passes	Wear out, [latex]h ^ {\kern 0.04em \prime} (t) \ge 0[/latex]>	Deteriorating, [latex]\lambda ^ \prime (t) \ge 0[/latex]

The notation that applies to all three point process models surveyed in this section is presented next.

In the point processes discussed in this section, failures occur at times [latex]T_1, \, T_2, \, \ldots \,[/latex], and the time to replace or repair an item is assumed to be negligible. The origin is defined to be [latex]T_0 = 0[/latex]. The times between the failures are [latex]X_1, \, X_2, \, \ldots \,[/latex], so T_k = [latex]X_1 + X_2 + \cdots + X_k[/latex], for [latex]k = 1, \, 2, \, \ldots \ \,[/latex]. The counting function [latex]N(t)[/latex] is the number of failures that occur in the time interval [latex](0, \, t][/latex]. In other words,

$\begin{array}{l} N (t) = max {k | T_{k} \leq t} \end{array}$

for [latex]t > 0[/latex]. The nondecreasing, integer-valued stochastic process described by [latex]\{N(t), \, t > 0 \}[/latex] is often called a counting process and satisfies the following two properties.

If [latex]t_1 < t_2[/latex], then [latex]N(t_1) \le N(t_2)[/latex].
If [latex]t_1 < t_2[/latex], then [latex]N(t_2) - N(t_1)[/latex] is the number of failures in the time interval [latex](t_1, \, t_2][/latex].

Let [latex]\Lambda (t) = E[N(t)][/latex] be the expected number of failures that occur in the interval [latex](0, \, t][/latex]. The derivative of [latex]\Lambda (t)[/latex], which is [latex]\lambda (t) = \Lambda ^ \prime (t)[/latex], is the rate of occurrence of failures. Figure 6.10 shows one realization of a point process, where [latex]N(t)[/latex] is shown as a step function and the ×s denote the failure times on the horizontal axis. The curve for the expected number of events by time t, [latex]\Lambda (t)[/latex], is also on the same axis as [latex]N(t)[/latex]. It should be kept in mind that [latex]N(t)[/latex] on this axis is a realization that will change from one item to another item, but [latex]\Lambda (t)[/latex] is the underlying population probabilistic mechanism describing the sequence of events and does not change from one item to another item.

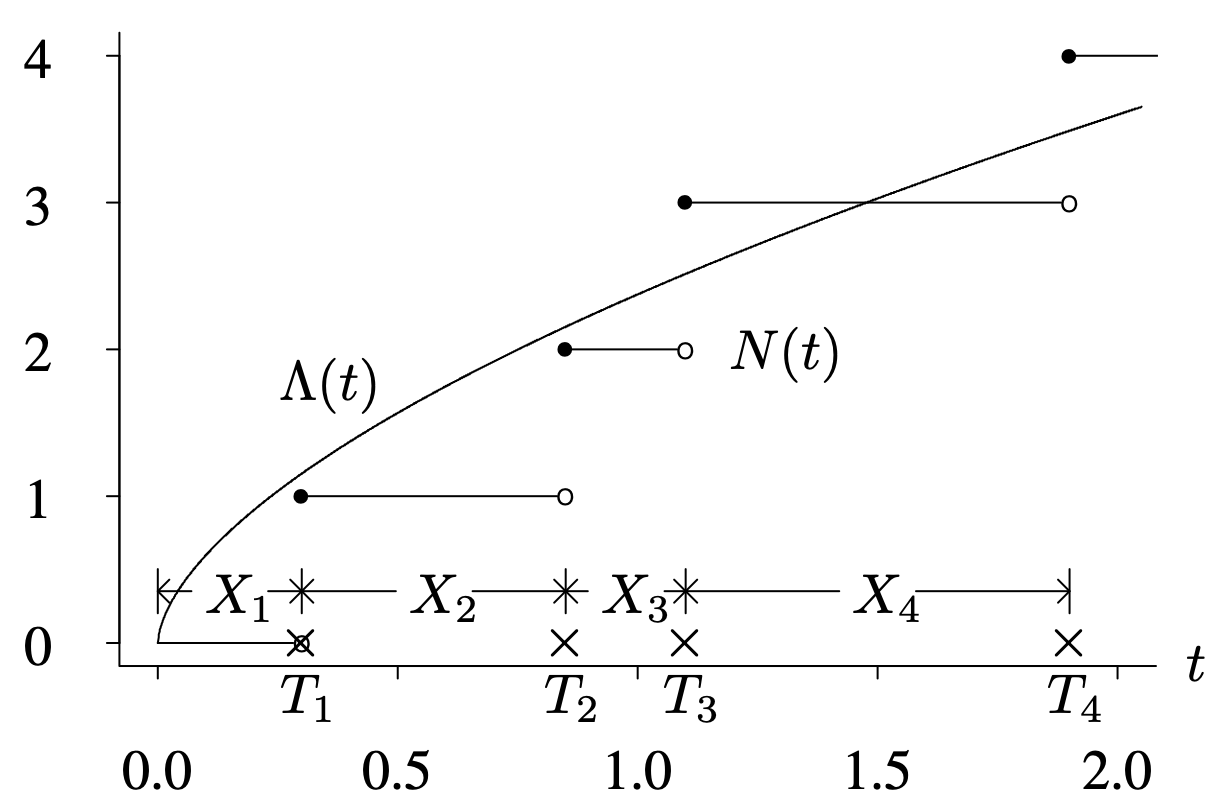
A graph of the counting function, with the expected number of failures. — Figure 6.10: Point process realization.

Long Description for Figure 6.10

The horizontal axis t ranges from 0.0 to 2.0 in increments of 0.5 units. The vertical axis ranges from 0 to 4 in increments of 1 unit. The discontinuous increasing step function has several horizontal segments, each with a solid dot at the left end and an open dot at the right as follows. from (0.25, 1) to (0.8, 1), from (0.8, 2) to (1.1, 2), and from (1.1, 3) to (1.9, 3). The X marks are plotted on the horizontal axis at t values 0.25, 0.8, 1.1, and 1.9 which are marked as T 1, T 2, T 3, and T 4, respectively. The horizontal distance from the origin to tick mark T 1 is X 1, and the remaining horizontal line segments have lengths X 2, X 3, and X 4, respectively. The counting function begins from the origin and increases through (0.75, 2), (1.5, 3), and (2, 3.5).

The behavior of the interevent times [latex]X_1, \, X_2, \, \ldots[/latex] is always of interest in analyzing a repairable item. If the interevent times tend to increase with time, the item is improving; if the interevent times tend to decrease with time, the item is deteriorating. Other variables, such as a new untrained operator or repairman, must be considered when analyzing the failure times of a repairable item. These variables are ignored in the presentation of the point process models, but can result in erroneous conclusions if not considered along with the observed times between failures.

There are two properties that are important to discuss before introducing specific point processes. The first property is called independent increments. A point process has independent increments if the number of failures in mutually exclusive intervals are independent. As shown in the realization depicted in Figure 6.11, this property implies that the number of failures (the failure times are depicted by ×s) between times t₁ and t₂ are independent of the number of failures between times t₃ and t₄ because the intervals [latex](t_1, \, t_2][/latex] and [latex](t_3, \, t_4][/latex] are nonoverlapping. A second property is called stationarity. A point process is stationary if the distribution of the number of failures in any time interval depends only on the length of the time interval. Equivalently, failures are no more or less likely to occur at one time than another for an item. This is a rather restrictive assumption for an item because the item can neither deteriorate nor improve.

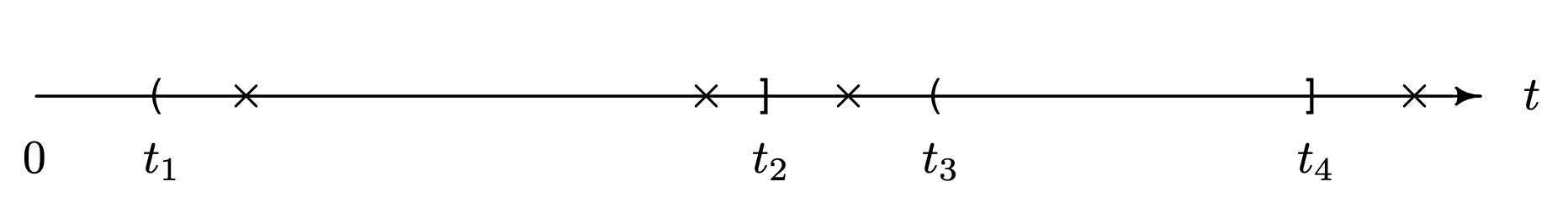
A horizontal line t ranges from 0 and is marked with times t 1, t 2, t 3, and t 4 at irregular intervals. There is an open parenthesis at t 1 and a closed square bracket at t 2. Two X marks are plotted on the line in this interval, one lying near t 1 and the other lying near t 2. Another X mark is plotted between times t 2 and t 3. There is an open parenthesis at t 3 and a closed square bracket at t 4. There is an X mark to the right of t 4. — Figure 6.11: Independent increments illustration.

The three point process models, Poisson processes, renewal processes, and nonhomogeneous Poisson processes, are introduced in separate subsections.

6.3.1 Poisson Processes

The well-known Poisson process is a popular model due to its mathematical tractability, although it applies only to limited situations. These limited situations include replacement models with exponential standby items and repairable items with exponential times to failure and negligible repair times.

There are several implications of this definition of a Poisson process. First, by the last condition for a Poisson process, the distribution of the number of failures in the interval [latex](t_1, \, t_2][/latex] has the Poisson distribution with parameter [latex]\lambda (t_2 - t_1)[/latex]. Therefore, the probability mass function of the number of failures in the interval [latex](t_1, \, t_2][/latex] is

$\begin{array}{l} P (N (t_{2}) - N (t_{1}) = x) = \frac{[λ (t_{2} - t_{1})]^{x} e^{- λ (t_{2} - t_{1})}}{x!} x = 0, 1, 2, \dots . \end{array}$

Second, the number of failures by time t, denoted by [latex]N(t)[/latex], has the Poisson distribution with population mean

$\begin{array}{l} Λ (t) = E [N (t)] = λ t t > 0, \end{array}$

where λ is often called the rate of occurrence of failures. The intensity function is therefore given by [latex]\lambda (t) = \Lambda ^ \prime (t) = \lambda[/latex] for [latex]t > 0[/latex]. Third, if [latex]X_1, \, X_2, \, \ldots[/latex] are independent and identically distributed exponential random variables, then [latex]N(t)[/latex] corresponds to a Poisson process.

Example 6.11 Consider a socket model in which an infinite supply of light bulbs is used in a single-component standby system composed of a single socket. As each bulb fails, it is immediately replaced by a new bulb, and each bulb has an exponential(λ) time to failure. Find the probability that there are n or fewer failures by time t.

Since the light bulb failure time distributions are each exponential, and the replacement time is negligible, a Poisson process is the appropriate model here. The probability that there are n or fewer failures by time t is therefore

$\begin{array}{l} P (N (t) \leq n) = \sum_{k = 0}^{n} \frac{(λ t)^{k} e^{- λ t}}{k!} n = 0, 1, 2, \dots \end{array}$

for [latex]t > 0[/latex]. When [latex]n = 0[/latex], this solution reduces to the survivor function for an exponential distribution (the nonrepairable case). It is easily recognized here that the time of the nth failure has the Erlang distribution with scale parameter λ and shape parameter n because [latex]T_n = X_1 + X_2 + \cdots + X_n[/latex] and [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are independent and identically distributed exponential(λ) random variables.

This model is sometimes also called a homogeneous Poisson process because the failure rate λ does not change with time (that is, the model is stationary). The next two models are generalizations of homogeneous Poisson processes. In a renewal process, the assumption of exponentially distributed times between failures is relaxed; in a nonhomogeneous Poisson process, the stationarity assumption is relaxed.

6.3.2 Renewal Processes

A renewal process is a natural extension of a Poisson process in which the times between failure are assumed to have any lifetime distribution, rather than just the exponential distribution.

The term renewal is appropriate for these models because an item is assumed to be renewed to its original state after it fails. This is typically not the case for a repairable system consisting of many components, because only a few of the components are typically replaced upon failure. The remaining components that did not fail will only be as good as new if they have exponential lifetimes. Renewal processes are often used, for example, to determine the number of spare components to take on a mission or to determine the timing of a sequence of repairs.

One classification of renewal processes that is useful in the study of socket models concerns the coefficient of variation [latex]\gamma = \sigma / \mu[/latex] of the distribution of the times between failures. This classification divides renewal processes into underdispersed and overdispersed processes.

Figure 6.12 displays realizations of three different renewal process. The first process is underdispersed because the coefficient of variation of the distribution of the time between failures is less than 1. An extreme case of an underdispersed process is one in which the coefficient of variation of the distribution of the time between failures is 0 (that is, a deterministic failure time for each item because [latex]\sigma / \mu = 0[/latex] implies that [latex]\sigma = 0[/latex]), which would yield a deterministic renewal process. The underdispersed process is much more regular in its failure times; hence, it is easier to determine when it is appropriate to replace an item if failure is catastrophic or expensive. A design engineer’s goal might be to reduce the variability of the lifetime of an item, which in turn decreases the coefficient of variation. Reduced variation with increased mean is desirable for most items. The second axis in Figure 6.12 corresponds to a realization of a renewal process that has a coefficient of variation of the distribution of the time between failures equal to 1. This case sits in between the underdispersed and overdispersed cases. There is more clumping of failures than in the underdispersed case. The third axis corresponds to a realization of an overdispersed distribution. There is extreme clumping of failures here, and many failures occur soon after an item is placed into service. Fortunately, the overdispersed case occurs less often in practice than the underdispersed case.

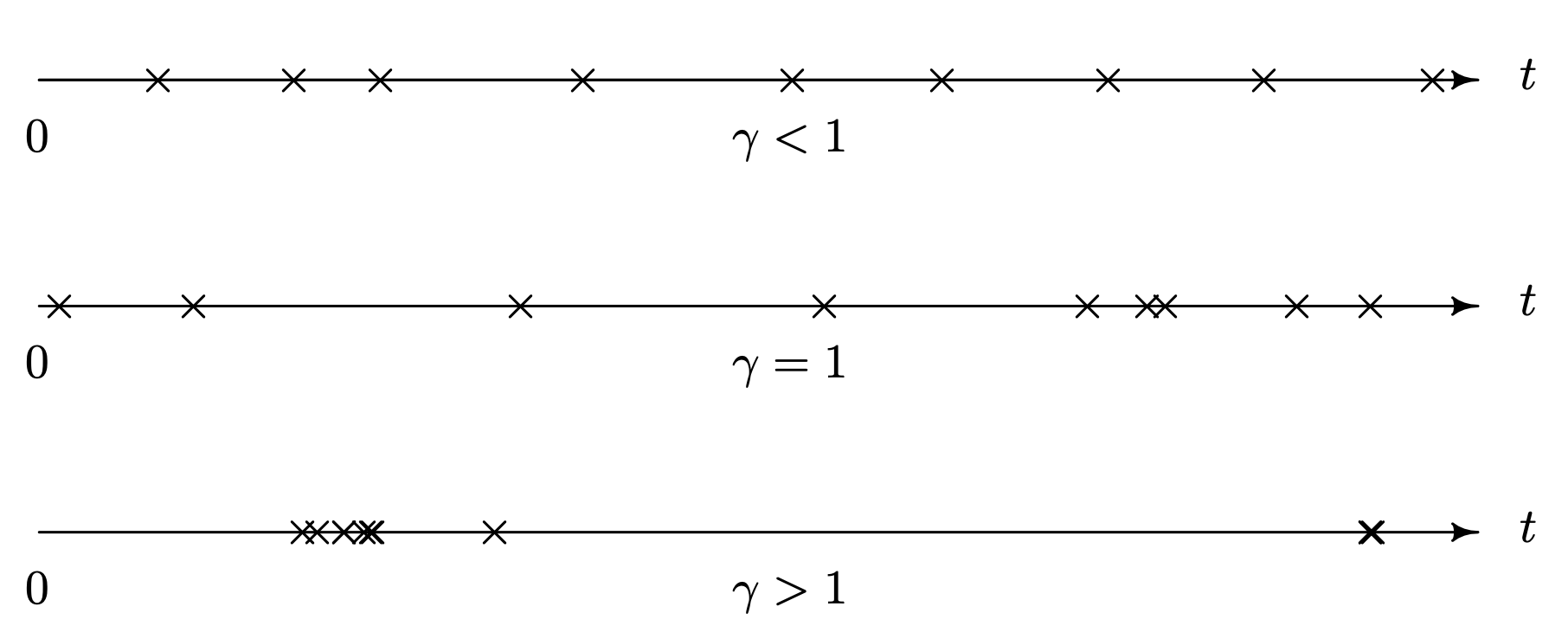
Three different renewal processes of realization, based on the coefficient of variation. — Figure 6.12: Classifying renewal processes based on the coefficient of variation.

Long Description for Figure 6.12

All three processes have a horizontal line t ranges from 0 and have several X marks. The first process has a coefficient of variation gamma less than 1. Here, nine X marks are almost equally spaced on the horizontal line. The second process has a coefficient of variation gamma equals 1. The first four X marks are separated from each other, and the last five X marks are close together. The third process has a coefficient of variation gamma greater than 1. Here, the first six X marks form a cluster on the left end, followed by the seventh X mark which apart from the cluster. The eighth and the ninth X marks are overlapped, and lie on the right end, apart from the remaining X marks.

Example 6.12 Consider a renewal process with Weibull([latex]\lambda, \, \kappa[/latex]) time between failures. Classify the renewal processes into the underdispersed and overdispersed cases.

The shape parameter [latex]\kappa[/latex] partitions the renewal process into the various cases. When [latex]\kappa > 1[/latex], the process is underdispersed; when [latex]\kappa < 1[/latex], the process is overdispersed; when [latex]\kappa = 1[/latex], the process reduces to a Poisson process because the time between failures is exponential(λ). The sequence of failures depicted on the time axes in Figure 6.12 were generated by Monte Carlo simulation using Weibull([latex]\lambda, \, \kappa[/latex]) times between failures. The top axis corresponds to [latex]\kappa = 5[/latex] (an IFR time between failures distribution) and the pattern of failures reflects the relatively small standard deviation of the time between failures distribution. The middle axis corresponds to [latex]\kappa = 1[/latex] (the exponential special case of the Weibull distribution), so this is a realization of a Poisson process. This case is the dividing line between an underdispersed renewal process and an overdispersed renewal process. There is more clumping of failures than in the underdispersed case because the mode of the exponential distribution is zero. A replacement policy is ineffective in this case because of the memoryless property of the exponential distribution. The bottom axis corresponds to [latex]\kappa = 1 / 2[/latex] (a DFR time between failures distribution), and the clumping of failures becomes even more extreme. On all three axes, there are nine failures, but the pattern of failures differs significantly for the various values of [latex]\kappa[/latex].

Two measures of interest that often arise when using a renewal process are the distribution of T_n, the time of the nth failure, and the distribution of the number of failures by time t. In terms of the distribution of T_n, there are simple results for the expected value and population variance of T_n, but the tractability of the distribution of T_n depends on the tractability of the distribution of the times between failures. Since [latex]T_n = X_1 + X_2 + \cdots + X_n[/latex], and the X_i‘s are mutually independent and identically distributed, the expected value and population variance of T_n are

$\begin{array}{l} E [T_{n}] = n E [X] and V [T_{n}] = n V [X], \end{array}$

where E[X] and V[X] are the expected value and population variance of the time between failures. The survivor function for the time of the nth failure, [latex]S_{T_n}(t) = P(T_n \ge t)[/latex], can be found as a function of the distribution of the X_i‘s and is tractable only for simple time between failure distributions.

The distribution of the number of failures by time t can be calculated by finding the values of the mass function [latex]P\big(N(t) = n\big)[/latex] for all values of n. Since exactly n failures occurring by time t is equivalent to T_n being less than or equal to t and [latex]T_{n + 1}[/latex] being greater than t,

$\begin{array}{l} P (N (t) = n) & = P (T_{n} \leq t < T_{n + 1}) \\ = P (T_{n + 1} \geq t) - P (T_{n} \geq t) \\ = S_{T_{n + 1}} (t) - S_{T_{n}} (t) \end{array}$

for [latex]n = 0, \, 1, \, 2, \, \ldots[/latex] and [latex]t > 0[/latex], and continuous time between failures distribution. Although using the exponential distribution as the time to failure for each item reduces a renewal process to a Poisson process, it will be used in the next example because it is one of the few distributions for which these measures can easily be calculated.

Example 6.13 Consider again a socket model for which the time to failure of each light bulb inserted in the socket has an exponential distribution with failure rate λ. Find the expected value and the population variance of T_n, the survivor function of T_n, and the probability mass function of the number of failures by time t.

First, since each item has population mean time to failure [latex]E[X] = 1 / \lambda[/latex], and population variance of the time to failure [latex]V[X] = 1 / \lambda ^ 2[/latex], the expected value and the population variance of the time of failure n are

$\begin{array}{l} E [T_{n}] = n E [X] = \frac{n}{λ} and V [T_{n}] = n V [X] = \frac{n}{λ^{2}} \end{array}$

for [latex]n = 0, \, 1, \, 2, \, \ldots[/latex]. Since T_n is the sum of independent and identically distributed exponential random variables, it has the Erlang distribution with survivor function

$\begin{array}{l} S_{T_{n}} (t) = \sum_{k = 0}^{n - 1} \frac{(λ t)^{k}}{k!} e^{- λ t} t > 0 \end{array}$

for [latex]n = 1, \, 2, \, \ldots[/latex]. To find the probability mass function for the number of failures by time t,

$\begin{array}{l} P (N (t) = n) & = S_{T_{n + 1}} (t) - S_{T_{n}} (t) \\ = \sum_{k = 0}^{n} \frac{(λ t)^{k}}{k!} e^{- λ t} - \sum_{k = 0}^{n - 1} \frac{(λ t)^{k}}{k!} e^{- λ t} \\ = \frac{(λ t)^{n}}{n!} e^{- λ t} \end{array}$

for [latex]n = 0, \, 1, \, 2, \, \ldots[/latex], and [latex]t > 0[/latex], which is recognized as the Poisson distribution with rate parameter [latex]\lambda \kern 0.02em t[/latex]. This simplest case of a renewal process corresponds to a Poisson process.

A more mathematically complicated situation occurs when the gamma distribution is used to model the time between failures.

Example 6.14 Consider a socket model with a single socket in which the lifetime of each light bulb to be placed in the socket has the gamma distribution with scale parameter [latex]\lambda = 0.001[/latex] and shape parameter [latex]\kappa = 5.2[/latex], where time is measured in hours. Find the probability that three light bulbs are sufficient to light the system for 8760 hours (one year).

Since the mean of the gamma distribution is [latex]\kappa / \lambda[/latex], each light bulb has mean time to failure [latex]\mu = 5.2/0.001 = 5200[/latex] hours. Thus, the expected time of failure number [latex]n = 3[/latex] is [latex]E\left[ T_3 \right] = 3 E[X] = 3 (5200) = \text{15,600}[/latex] hours, or almost two years. This preliminary analysis indicates that the probability that three bulbs will be sufficient for one year of operation should be fairly high.

A result that can be used to determine the exact probability is that the sum of n independent and identically distributed gamma random variables also has a gamma distribution. This result is most easily derived by using the moment generating function approach to determine the distribution of the sum of independent random variables. Let the random variable X have a gamma distribution with parameters λ and [latex]\kappa[/latex]. The moment generating function of X is

$\begin{array}{l} M_{X} (s) & = E [e^{s X}] \\ = \int_{0}^{\infty} e^{s x} \frac{λ}{Γ (κ)} (λ x)^{κ - 1} e^{- λ x} d x \\ = \frac{λ^{κ}}{Γ (κ)} \int_{0}^{\infty} x^{κ - 1} e^{- x (λ - s)} d x \\ = \frac{λ^{κ}}{Γ (κ)} \int_{0}^{\infty} {(\frac{u}{λ - s})}^{κ - 1} e^{- u} \frac{1}{λ - s} d u \\ = {(\frac{λ}{λ - s})}^{κ} \frac{1}{Γ (κ)} \int_{0}^{\infty} u^{κ - 1} e^{- u} d u \\ = {(\frac{λ}{λ - s})}^{κ} \end{array}$

for all [latex]s < \lambda[/latex]. Since [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are mutually independent and identically distributed gamma random variables, the moment generating function of [latex]T_n = X_1 + X_2 + \cdots + X_n[/latex] is the product of n of these moment generating functions:

$\begin{array}{l} M_{T_{n}} (s) = \prod_{i = 1}^{n} M_{X_{i}} (s) = {(\frac{λ}{λ - s})}^{n κ} \end{array}$

for all [latex]s < \lambda[/latex]. Thus, if [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are independent and identically distributed gamma random variables with parameters λ and [latex]\kappa[/latex], then the probability distribution of their sum has the gamma distribution with parameters λ and [latex]n \kappa[/latex]. For the problem at hand, the time to the third failure, T₃, has a gamma distribution with scale parameter λ = 0.001 and shape parameter [latex]n \kappa = (3)(5.2) = 15.6[/latex]. To find the probability that T₃ exceeds 8760,

$\begin{array}{l} P (T_{3} \geq 8760) = S_{T_{3}} (8760) = 1 - I (15.6, 8.76) = 0.9771, \end{array}$

where I is the incomplete gamma function. The R statement below computes this probability using the pgamma function, which returns the cumulative distribution function of a random variable having the gamma distribution.

This completes the brief introduction to renewal processes. The final subsection introduces nonhomogeneous Poisson processes.

6.3.3 Nonhomogeneous Poisson Processes

The third and final point process introduced here is the nonhomogeneous Poisson process. There are at least four reasons that a nonhomogeneous Poisson process should be considered for modeling the sequence of failures of a repairable item.

A homogeneous Poisson process is a special case of a nonhomogeneous Poisson process.
The probabilistic model for a nonhomogeneous Poisson process is mathematically tractable.
The statistical methods for a nonhomogeneous Poisson process are mathematically tractable.
Unlike a homogeneous Poisson process or a renewal process, a nonhomogeneous Poisson process is able to model the failure times of improving and deteriorating items.

One disadvantage with both Poisson processes and renewal processes is that they assume that the distribution of the time to failure for each item in a socket model with a single socket is identical. This means that it is not possible for the item to improve or deteriorate. A nonhomogeneous Poisson process is another generalization of the homogeneous Poisson process for which the stationarity assumption is relaxed. Instead of a constant rate of occurrence of failures λ, as in a homogeneous Poisson process, this rate varies over time according to [latex]\lambda (t)[/latex], which is often called the intensity function. The cumulative intensity function is defined by

$\begin{array}{l} Λ (t) = \int_{0}^{t} λ (τ) d τ \end{array}$

and is interpreted as the expected number of failures by time t. These two functions are generally used to describe the probabilistic mechanism governing the failure times of the item, as opposed to the five distribution representations used to describe the time to failure of nonrepairable items.

Thus, if the intensity function is decreasing, the item is improving; if the intensity function is increasing, the item is deteriorating. For nonhomogeneous Poisson processes, the times between failures are neither independent nor identically distributed. The time to the first failure in a nonhomogeneous Poisson process has the same distribution as the time to failure of a nonrepairable item with hazard function [latex]h(t) = \lambda (t)[/latex]. Subsequent failures follow a conditional version of the intensity function that does not depend on previous values of [latex]\lambda (t)[/latex]. The times between these subsequent failures do not necessarily follow any of the probability distributions (for example, the Weibull distribution) used in survival analysis.

Since the independent increments property has been retained from the definition of a homogeneous Poisson process, this model assumes that previous failure times do not affect the future failure times of the item. Although this may not be exactly true in practice, the nonhomogeneous Poisson process model is still valuable because it is mathematically tractable and allows for improving and deteriorating systems. In addition, parameter estimation for the nonhomogeneous Poisson process model is simple, which is another attractive feature.

Example 6.15 Consider a nonhomogeneous Poisson process with intensity function

$\begin{array}{l} λ (t) = κ λ^{κ} t^{κ - 1} t > 0, \end{array}$

where λ and [latex]\kappa[/latex] are positive parameters. This intensity function can be recognized as the same functional form as the hazard function for a Weibull random variable with scale parameter λ and shape parameter [latex]\kappa[/latex], and is often referred to as a power law process. For this intensity function, if [latex]\kappa < 1[/latex], the item is improving because the intensity function is decreasing, if [latex]\kappa > 1[/latex], the item is deteriorating because intensity function is increasing, and if [latex]\kappa = 1[/latex], it reduces to a homogeneous Poisson process with rate parameter λ. Find the probability that there will be exactly n failures by time t. Also, if failure n occurs at time t_n, find the conditional survivor function for the time to the next failure.

Using Definition 6.6, the number of failures by time t, [latex]N(t)[/latex], has probability mass function

$\begin{array}{l} P (N (t) = n) = \frac{{[\int_{0}^{t} λ (τ) d τ]}^{n} e^{- \int_{0}^{t} λ (τ) d τ}}{n!} n = 0, 1, 2, \dots \end{array}$

for [latex]t > 0[/latex]. Using the fact that [latex]\Lambda (t) = \displaystyle{\int_0^t \kappa \kern 0.02em \lambda^{\kappa} \tau^{\kappa - 1} d \tau} = (\lambda \kern 0.02em t)^{\kappa}[/latex] for [latex]t > 0[/latex],

$\begin{array}{l} P (N (t) = n) = \frac{(λ t)^{κ n} e^{- (λ t)^{κ}}}{n!} n = 0, 1, 2, \dots \end{array}$

for [latex]t > 0[/latex]. Finding the survivor function for the time to the next failure involves conditioning. Using independent increments, the fact that [latex]S(t) = e^{-H(t)}[/latex], and conditioning, the conditional survivor function for the time to the next failure is

$\begin{array}{l} S_{T | T > t_{n}} (t) = e^{- (Λ (t) - Λ (t_{n}))} = e^{- ((λ t)^{κ} - (λ t_{n})^{κ})} = e^{- λ^{κ} (t^{κ} - t_{n}^{κ})} t > t_{n} . \end{array}$

It was stated earlier that point process models are used in applications outside of reliability. Figure 6.13 provides an example in which the event of interest is an arrival of a car to a drive-up window at a fast food restaurant rather than the usual failure time of a repairable item. The intensity function [latex]\lambda(t)[/latex] models the arrival rate to the drive-up window, which has peaks at breakfast, lunch, and dinner times. The highest peak is at lunch when the intensity function is about 6 cars per hour. Each × along the time axis denotes an arrival time of a car to the drive-up window, and the clusters during the three meal times are apparent in the realization. The height of the intensity function is proportional to the probability of an arrival rate in the next instant. As was the case before, the arrival time values will vary from one realization to the next for the fixed intensity function illustrated in Figure 6.13.

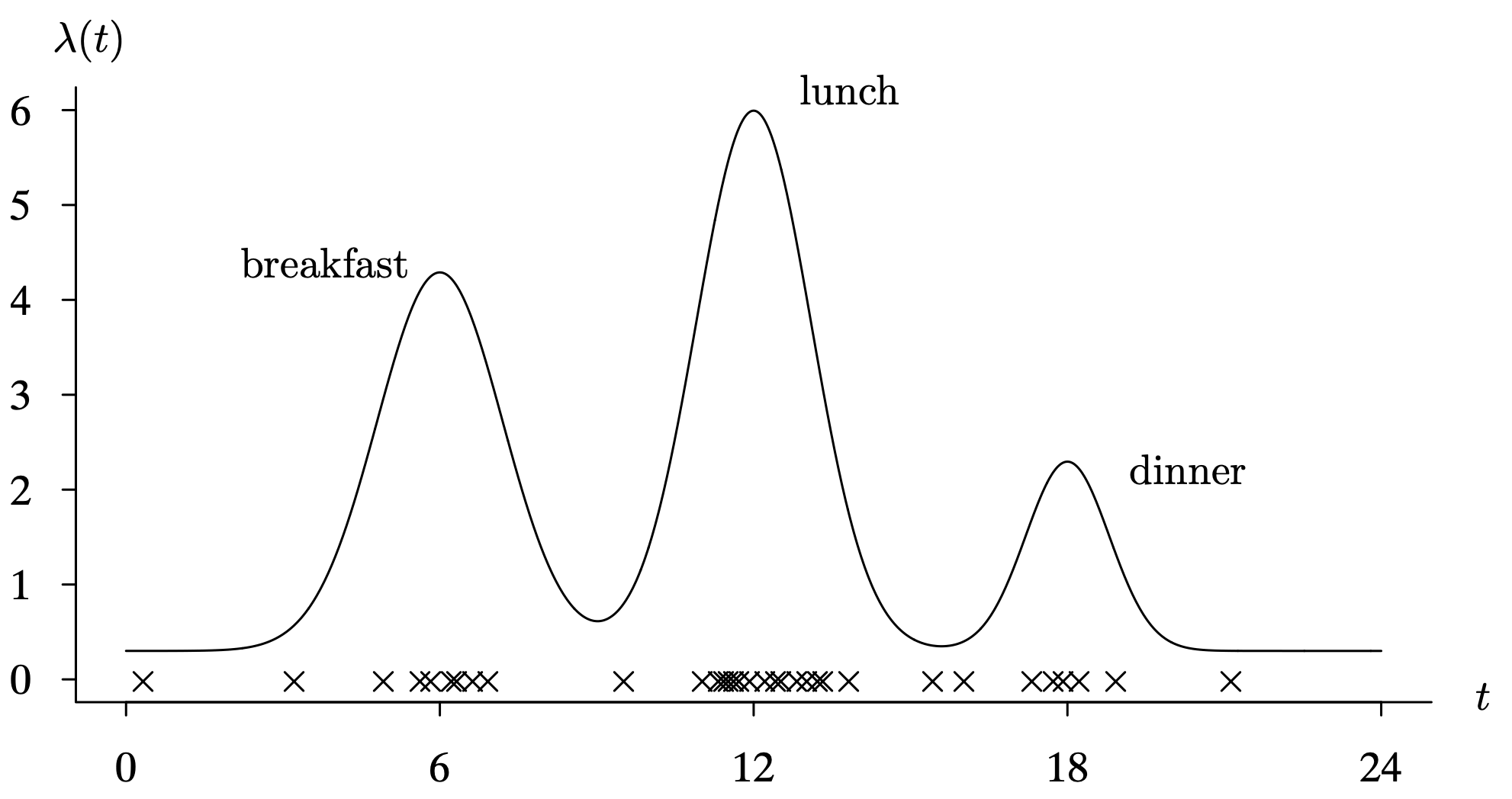
A graph of an intensity function, with three peaks for the arrival of a car to a drive up window. — Figure 6.13: Intensity function for arrivals to a fast food restaurant drive-up window.

Long Description for Figure 6.13

The horizontal axis t ranges from 0 to 24 in increments of 6 units. The vertical axis lambda of t ranges from 0 to 6 in increments of 1 unit. The intensity function has three peaks at breakfast, lunch, and dinner from left to right. The highest peak is for lunch at (12, 6), the second highest peak is for breakfast with an intensity of (6, 4), and the third peak for dinner has an intensity of (18, 2). The X marks are plotted on the horizontal axis. The cluster of X marks is for breakfast, the major cluster is for lunch, and the small cluster is for lunch. All data are estimated.

The renewal process and the nonhomogeneous Poisson process are the two most popular point process models for modeling the underlying probability mechanism associated with the failure times of a repairable item. The two models are at the extremes of the repair action associated with a repairable item with a negligible repair time. One can think of the failures and repairs in a renewal process as perfect repairs, in which the item is completely restored to a new item. One can think of the failures and repairs in a nonhomogeneous Poisson process as minimal repairs, in which the item continues along the same intensity function track that was in play prior to the failure. The terms perfect repair and minimal repair for an item (that is, a component or a system) are defined next.

There are two ways to think about a perfect repair. One way to perform a perfect repair is to discard the failed item and simply replace it with a new item. This is the case with replacement or socket model. A second way to perform a perfect repair is to perform the repair in a manner which makes the item as good as new with respect to its lifetime distribution. Regardless of which of these options occurs in practice, a renewal process is the appropriate probabilistic model to capture the time evolution of the repairable item. If all repairs on an item are perfect, then the times between failure are mutually independent and identically distributed random variables.

A nonhomogeneous Poisson process model can provide a reasonable underlying probability model for the failure sequence for a series system comprised of hundreds, or even thousands of components with roughly equal reliabilities. A component which fails and is replaced or repaired leaves the system in nearly the same condition as it was just prior to the failure. The failed component is such a small part of the overall system that using a minimal repair is appropriate.

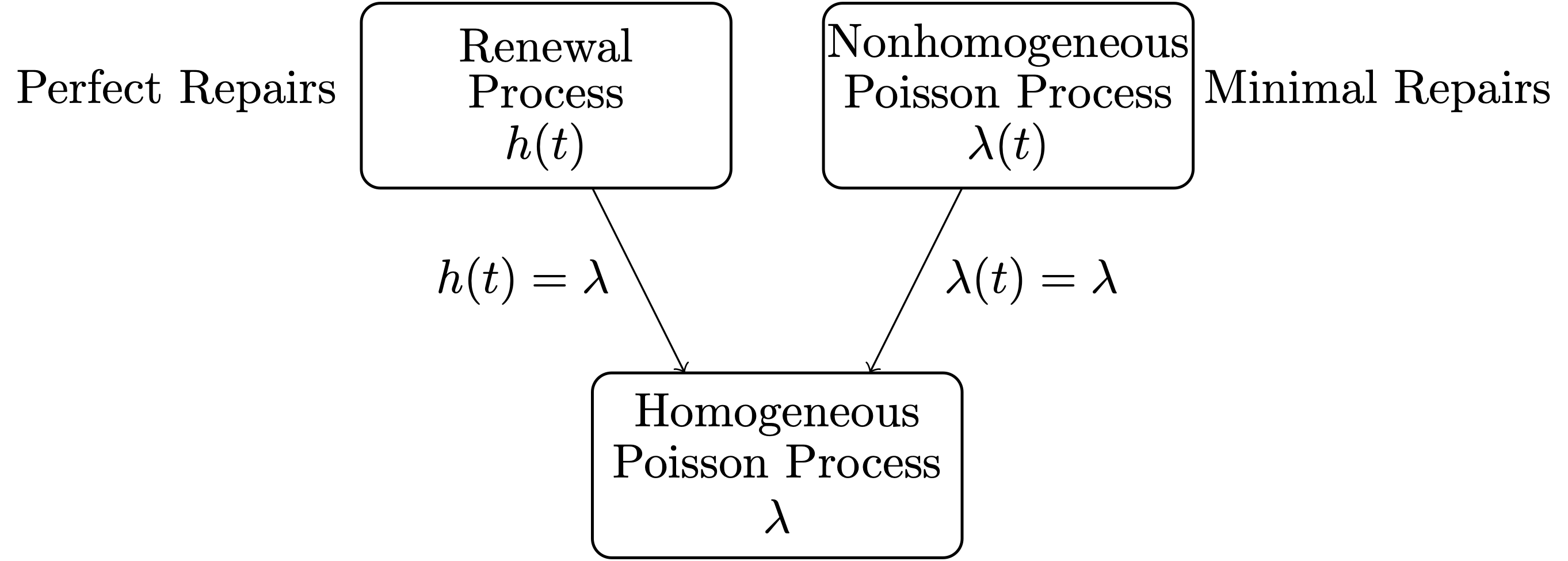
A graphic presents the relationship between the three point process models — Figure 6.14: Relationships between point processes.

Long Description for Figure 6.14

Three point process models are renewal process h of t, nonhomogeneous Poisson process lambda of t, and homogeneous Poisson Process lambda. The renewal process has perfect repair and collapses to a homogeneous Poisson process with the label h of t equals lambda. The nonhomogeneous Poisson process has minimal repairs and collapses to the homogeneous Poisson process with the label lambda of t equals lambda.

Figure 6.14 shows the relationship between the three point process models that have been presented in this section. A renewal process is defined by the probability distribution of the time between events. These events are failures in reliability modeling. This probability distribution can be defined by any of the five lifetime distribution representations defined in Section 4.1. Figure 6.14 uses the hazard function to define the probability distribution of the time between failures. A renewal process collapses to a homogeneous Poisson process with positive rate λ when

$\begin{array}{l} h (t) = λ t > 0. \end{array}$

A nonhomogeneous Poisson process can be defined by the intensity function [latex]\lambda(t)[/latex] or the cumulative intensity function [latex]\Lambda(t)[/latex]. Figure 6.14 uses the intensity function [latex]\lambda(t)[/latex] to define the probabilistic mechanism governing the failure times. A nonhomogeneous Poisson process collapses to a homogeneous Poisson process with positive rate λ when

$\begin{array}{l} λ (t) = λ t > 0. \end{array}$

The hazard function was introduced in Section 4.1 as a rate of failure using limits. The conditional intensity function can be defined in a similar fashion. Let [latex]{\cal H}_{ \, t ^ -}[/latex] represent the history of an item from time zero until just prior to time t. The most informative way to think of [latex]{\cal H}_{ \, t ^ -}[/latex] is to consider it a record of the failure times associated with the counting process [latex]N(t)[/latex] for all time values from zero until just prior to t. Given this history, we can define the conditional intensity function as

$$
\lambda(t \, | \, {\cal H}_{ \, t ^ -} )
= \lim_{{\Delta} \kern 0.02em t \, \to \, 0}
\frac{P( \hbox{failure in the interval }
(t, \, t + \Delta \kern 0.02em t ] \,|\, {\cal H}_{ \, t ^ -} ) }
{\Delta \kern 0.02em t}.
$$

The conditional intensity function for an item having independent and identically distributed times to failure in the IFR class and perfect repairs is illustrated in Figure 6.15. This corresponds to the risk profile associated with one realization of a renewal process. Each × on the time axis corresponds to a failure and repair. Each failure and repair restores the item to a like new state, so the conditional intensity function evolves after the failure like that of a new item.

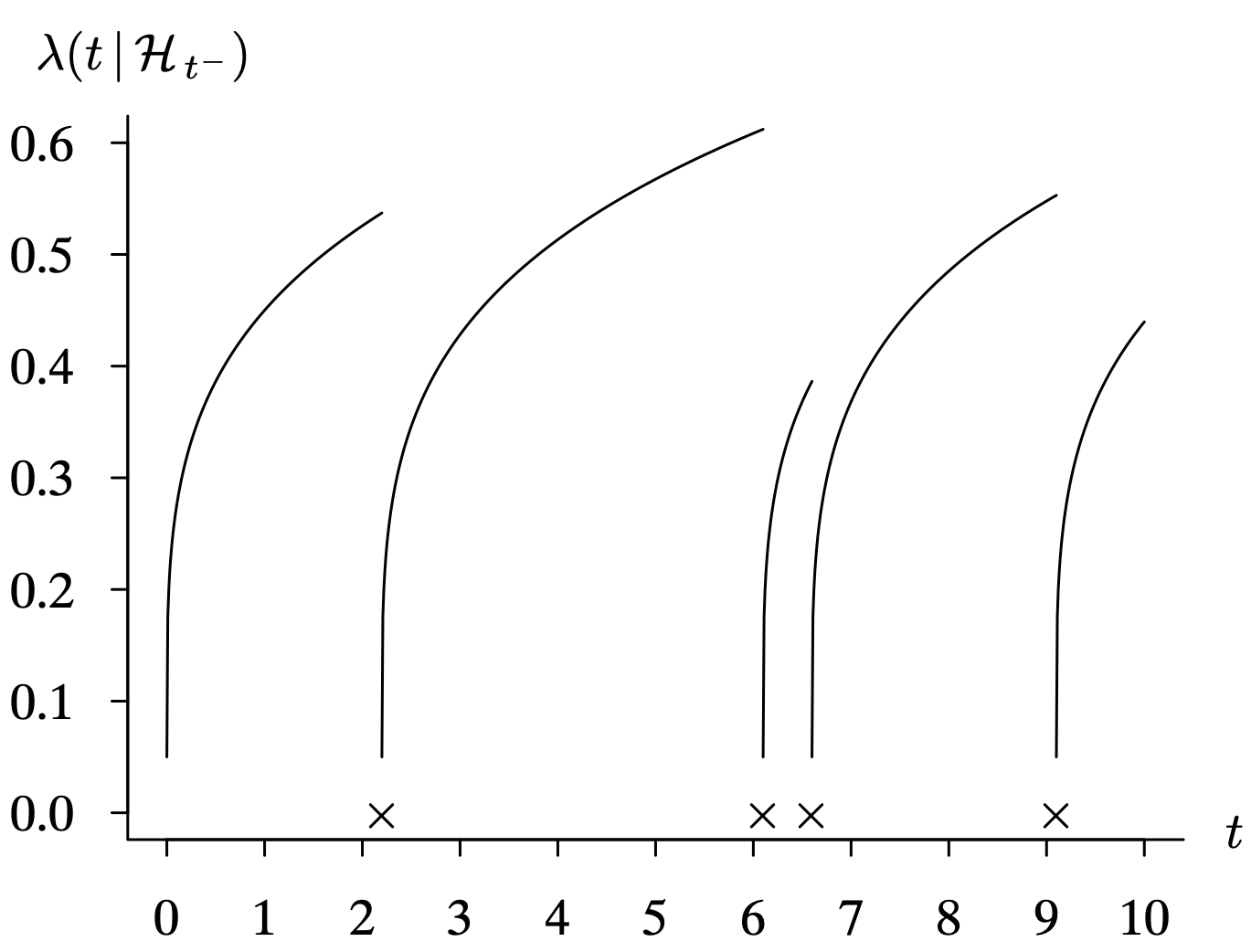
A graph of the conditional intensity function with five repairs. — Figure 6.15: Conditional intensity function for perfect repairs.

Long Description for Figure 6.15

The horizontal axis t measures time and ranges from 0 to 10 in increments of 1 unit. The vertical axis measures lambda of t such that H subscript t minus. It ranges from 0.0 to 0.6 in increments of 0.1 unit. The X marks are p at t equals 2.2, 6.1, 6.6, and 9. Five concave down increasing functions are drawn at t equals 0, 2.2, 6.1, 6.6, and 9, and all start with the intensity of 0.5. The first function increases to 0.55 at t equals 2, the second function increases to 0.6 at t equals 6, the third function increases to 0.36 at t equals 6.5, the fourth function increases to 0.55 at t equals 9, and the fifth function increases to 0.45 at t equals 10. All values are estimated.

The opposite extreme in terms of repair action is illustrated in Figure 6.16. This corresponds to the risk profile associated with one realization of a nonhomogeneous Poisson process. Each × on the time axis corresponds to a failure and a minimal repair which occurs in a negligible period of time. Each failure and minimal repair takes the item to the same condition as it was just prior to the failure in terms of its future risk. So each failure does not change the trajectory of [latex]\lambda(t)[/latex], which corresponds to a deteriorating item in this illustration.

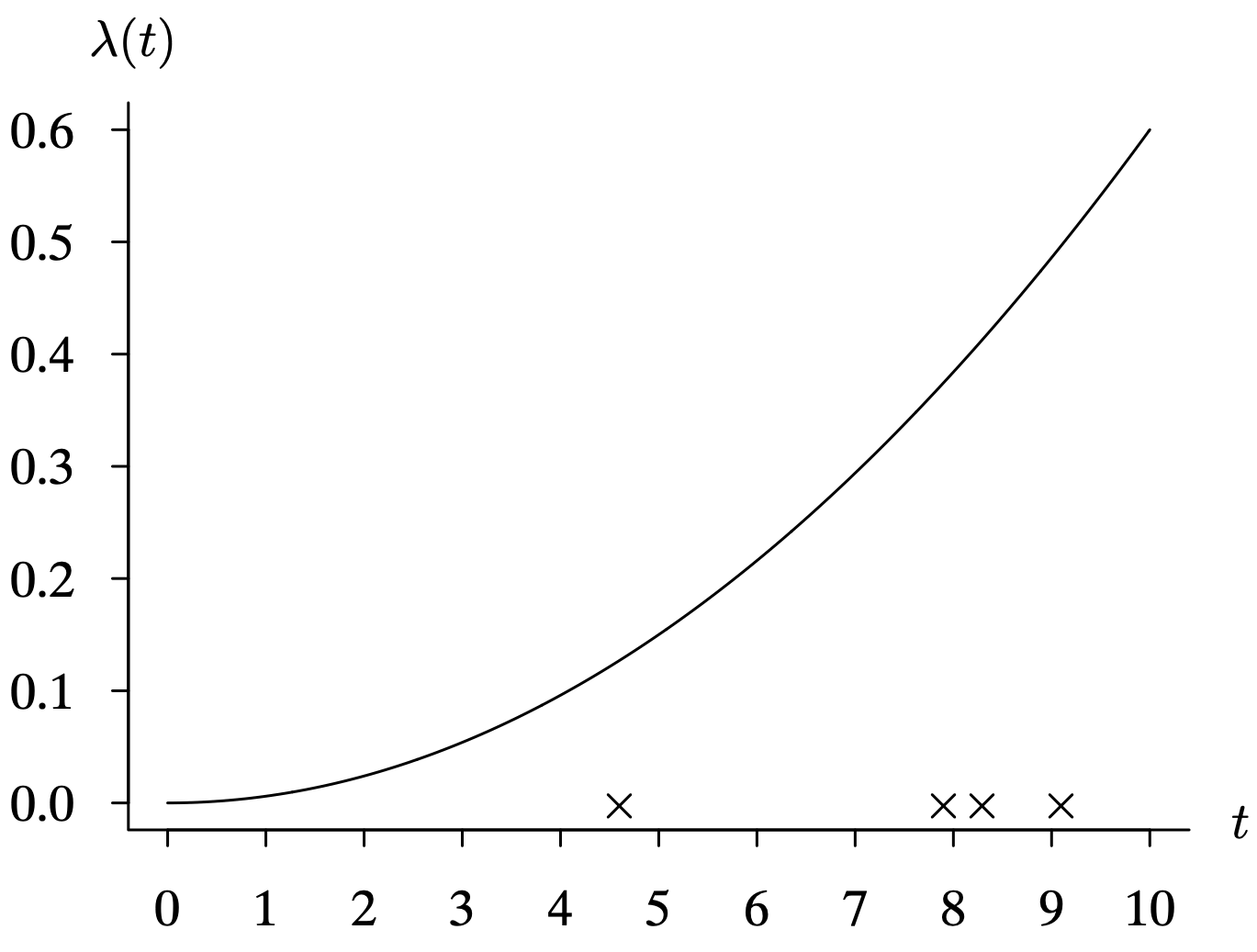
A graph of the conditional intensity function in terms of minimal repair action. — Figure 6.16: Conditional intensity function for minimal repairs.

Long Description for Figure 6.16

The horizontal axis represents time and ranges from 0 to 10 in increments of 1 unit. The vertical axis measures lambda of t and ranges from 0.0 to 0.6 in increments of 0.1 unit. The function increases exponentially through the points (0, 0.0), (4, 0.1), (8, 0.4), and (10, 0.6). All data are estimated.

There have been several schemes proposed for interpolating between renewal processes (to model perfect repairs) and nonhomogeneous Poisson processes (to model minimal repairs). One such scheme assigns a probability p to replacement of the entire item with a new item, which corresponds to a perfect repair, so that replacement or repair of just one of many components, which corresponds to a minimal repair, occurs with probability [latex]1 - p[/latex]. The extreme case of [latex]p = 0[/latex] corresponds to a nonhomogeneous Poisson process; the extreme case of [latex]p = 1[/latex] corresponds to a renewal process.

One final topic, superpositioning, can be applied to any of the three point process models considered thus far. Poisson, renewal, and nonhomogeneous Poisson processes are useful for modeling the failure pattern of a single repairable item. In some situations it is important to model the failure pattern of several items simultaneously. Examples include a job shop with k machines, a military mission with k weapons, or an item failing from one of k causes of failure. Figure 6.17 shows a superposition of the failure times of [latex]k = 3[/latex] items. The bottom axis contains the superposition of the three point process realizations on the top three axes. The superposition of several point processes is the ordered sequence of all failures that occur in any of the individual point processes. An important result that applies to superpositions of nonhomogeneous Poisson processes is: if [latex]\lambda_1 (t), \, \lambda_2 (t), \, \ldots, \, \lambda_k(t)[/latex] are the intensity functions for k independent items, then the intensity function for the superposition is [latex]\lambda (t) = \sum_{{i} \,=\, 1}^{k} \lambda_i (t)[/latex] for [latex]t > 0[/latex]. This result is similar to the result concerning the hazard functions for net lives in competing risks.

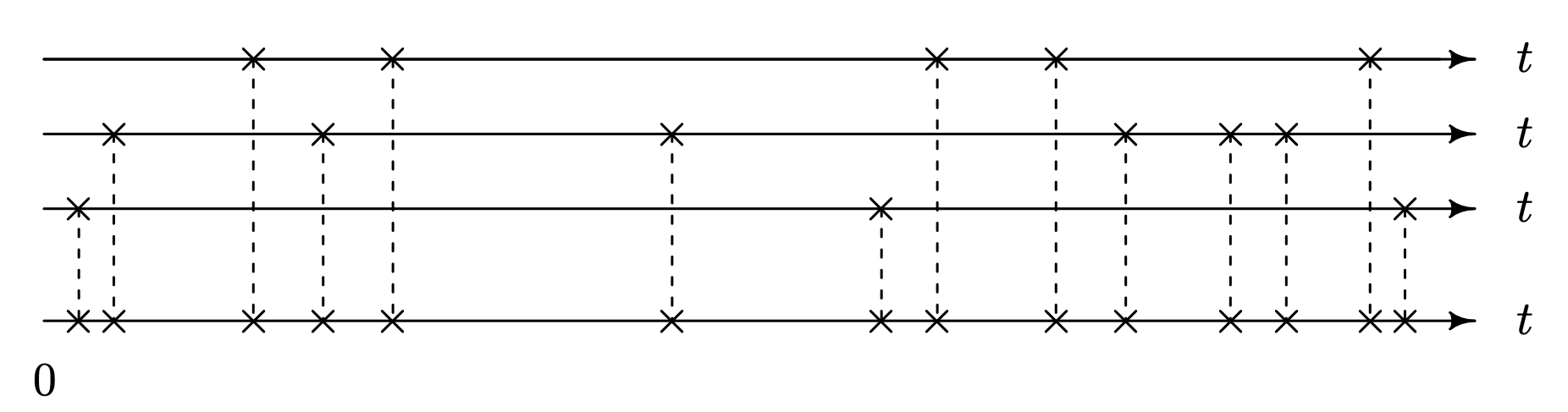
Four number lines, one of which exhibits the superimposition of the three point process realizations depicted on the other 3 lines. — Figure 6.17: Superposition of three point processes.

Long Description for Figure 6.17

All four lines are labeled t and are marked with X marks. The bottommost line has 14 X marks, of which the first five on the left end lie close to each other, the sixth one lies a little away from five X marks, and the last eight X marks lie close to each other. Above this are 3 number lines with X marks coinciding with the bottommost horizontal line. The bottom line has three X marks, the first mark aligns with the first mark, the second mark aligns with the seventh mark, and the third mark aligns with the last X mark of the bottommost horizontal line. The second line has six X marks. Those marks align with the second, fourth, sixth, tenth, eleventh, and twelfth tick marks of the bottommost number line, respectively. The top line has five X marks and are aligning with the third, fifth, eighth, ninth, and thirteenth marks of the bottommost horizontal line, respectively. The aligned X marks are connected by dotted vertical lines.

This ends the presentation of the three point process models considered here: Poisson processes, renewal processes, and nonhomogeneous Poisson processes. The first two models are only capable of modeling socket models for which the time between failures has a common distribution, whereas nonhomogeneous Poisson processes are capable of modeling improving and deteriorating systems, which are more common in practice. All three of these models are appropriate when there is a negligible down time (that is, failure and return to service occur at essentially the same point in time).

6.4 Exercises

6.1 The failure times of [latex]n = r = 20[/latex] electric generators (in hours) placed on an accelerated life test are

$\begin{array}{l} 7.5 121.5 279.8 592.1 711.5 848.2 1051.7 1425.5 1657.2 \\ 1883.6 2311.1 2951.2 5296.6 5637.9 6054.3 6303.9 6853.7 \\ 7201.9 9068.5 10, 609.7, \end{array}$

as given on page 101 of Zacks, S., Introduction to Reliability Analysis: Probabilistic Models and Statistical Methods, Springer–Verlag, Inc., New York, 1992.
1. Assuming that the time to failure of the population of generators at the accelerated conditions has the exponential distribution, find a point and 95% confidence interval estimate for the probability of survival to 6000 hours.
2. Using nonparametric methods, find a point and 95% confidence interval estimate for the probability of survival to 6000 hours under the accelerated conditions.
6.2 Show that the product–limit estimate reduces to the survivor function estimate for a complete data set when the failure times are distinct.
6.3 Show that the diagonal elements of the observed information matrix associated with the product–limit estimate are

$\begin{array}{l} {[- \frac{\partial^{2} \ln L (h (y_{1}), h (y_{2}), \dots, h (y_{k}))}{\partial h (y_{i})^{2}}]}_{h (y_{i}) = d_{i} / n_{i}} = \frac{n_{i}^{3}}{d_{i} (n_{i} - d_{i})} \end{array}$

for [latex]i=1,2,\ldots,k[/latex].
6.4 Find a point estimate and an approximate two-sided 95% confidence interval estimate for the probability that the remission times exceed 20 weeks for the control and treatment groups of the 6–MP data set from Example 5.6. Are there any conclusions that can be drawn from the two confidence intervals concerning the drug 6–MP’s influence on remission times exceeding 20 weeks?
6.5 Thirteen aircraft components are placed on a life test that is discontinued after the tenth failure. The failure times, in hours, are

$\begin{array}{l} 0.22 0.50 0.88 1.00 1.32 1.33 1.54 1.76 2.50 3.00, \end{array}$

as given on page 43 of Crowder, M.J., Kimber, A.C., Smith, R.L., and Sweeting, T.J., Statistical Analysis of Reliability Data, Chapman and Hall, New York, 1991.
1. Assuming that the time to failure of the components in the population has the exponential distribution, find a point and 95% confidence interval estimate for the probability of survival to 1.6 hours.
2. Using nonparametric methods, find a point and 95% confidence interval estimate for the probability of survival to 1.6 hours.
6.6 The survival times (in weeks) of patients with acute myelogenous leukemia in the nonmaintained group are

$\begin{array}{l} 5, 5, 8, 8, 12, 16^{*}, 23, 27, 30, 33, 43, 45, \end{array}$

where the * superscript signifies a right-censored observation, as given on page 49 of Miller, R., Survival Analysis, John Wiley & Sons, Inc., New York, 1981. Give a nonparametric estimator of the expected survival time of a patient with acute myelogenous leukemia in the nonmaintained group.

6.7 The failure times (in minutes) of electrical insulating fluid subjected to constant voltages below are from Nelson, W. B., “Graphical Analysis of Accelerated Life Test Data with the Inverse Power Law Model,” IEEE Transactions on Reliability, Vol. R–21, pp. 2–11, 1972.

Voltage (kV)	Failure time (minutes)
28	68.85	426.07	110.29	108.29	1067.6
30	17.05	22.66	21.02	175.88	139.07	144.12	20.46	43.40	194.90
	47.30	7.74
32	0.40	82.85	9.88	89.29	215.10	2.75	0.79	15.93	3.91
	0.27	0.69	100.58	27.80	13.95	53.24

Plot a nonparametric survivor function estimate for each of the three voltage levels on a single set of axes.
Fit the accelerated life model with an exponential baseline to the failure times. Report the maximum likelihood estimators and 95% confidence intervals (based on the observed information matrix) for all unknown parameters. Also, predict the mean time to failure at 26 kV voltage.

6.8 The lifetimes, in days, on [latex]n = 10[/latex] identical pieces of equipment are

$\begin{array}{l} 2 72^{*} 51 60^{*} 33 27 14 24 4 2 1^{*}, \end{array}$

as given in Lawless, J.F., Statistical Models and Methods for Lifetime Data, 2nd ed., John Wiley & Sons, Inc., Hoboken, NJ, 2003. The asterix denotes a right-censored observation. Assume that a random right censoring scheme is appropriate.
1. Find a nonparametric point estimate for [latex]S(25)[/latex].
2. Find a nonparametric 95% confidence interval for [latex]S(25)[/latex].
3. Use the relationship [latex]H(t) = -\ln \, S(t)[/latex] to determine a point estimate for [latex]H(25)[/latex] using your solution to part (a).
4. One other most popular technique for estimating [latex]H(t)[/latex] is the Nelson–Aalen estimator
  $\begin{array}{l} \hat{H} (t) = \sum_{j | y_{j} \leq t} \frac{d_{j}}{n_{j}}, \end{array}$
  
  where y_j, d_j, and n_j have the same meaning as in the Kaplan–Meier product–limit estimate. Give a point estimate for [latex]H(25)[/latex] using the Nelson–Aalen estimator.
5. Give a point estimate for [latex]S(25)[/latex] using the Nelson–Aalen estimator.
6.9 Find all possible values of the Kaplan–Meier product–limit estimate for the survivor function for n distinct failure and censoring values for [latex]n = 1, \, 2, \, \ldots, \, 10[/latex] and display these values in a graphic. Research in this area has been conducted by Qin, Y., Sasinowska, H., Leemis, L., “The Probability Mass Function of the Kaplan–Meier Product–Limit Estimator,” Forthcoming, The American Statistician, 2023.

6.10 One nonparametric technique for estimating the cumulative hazard function [latex]H(t)[/latex] is the Nelson–Aalen estimator:

$\begin{array}{l} \hat{H} (t) = \sum_{j | y_{j} \leq t} \frac{d_{j}}{n_{j}}, \end{array}$

where y_j, d_j, and n_j have the same meaning as in the Kaplan–Meier product–limit estimate. The observed failure times (in hours) of [latex]n = 4156[/latex] integrated circuits placed on a test that was terminated at 1370 hours given on page 5 of Meeker, W.Q., Escobar, L.A., Pascual, F.G., Statistical Methods for Reliability Data, 2nd ed., John Wiley & Sons, Inc., New York, 2022 are given in the table below. The ordered observed failure times are arranged in a row-wise fashion.

0.10	0.10	0.15	0.60	0.80	0.80	1.20
2.50	3.00	4.00	4.00	6.00	10.00	10.00
12.50	20.00	20.00	43.00	43.0	48.00	48.00
54.00	74.00	84.00	94.00	168.00	263.00	593.00

Give a point estimate for [latex]H(0.5)[/latex] using the Nelson–Aalen estimator.

6.11 Calculate the test statistic and the p-value for the log-rank test associated with the leukemia remission times in the control and treatment groups for the clinical trial involving 6–MP.
6.12 The remission times (in weeks) for 40 leukemia patients, with 20 patients selected at random and assigned to treatment A:

$\begin{array}{l} 1, 3, 3, 6, 7, 7, 10, 12, 14, 15, 18, 19, 22, 26, 28^{*}, 29, 34, 40, 48^{*}, 49^{*} \end{array}$

and the other 20 patients assigned to treatment B:

$\begin{array}{l} 1, 1, 2, 2, 3, 4, 5, 8, 8, 9, 11, 12, 14, 16, 18, 21, 27^{*}, 31, 38^{*}, 44. \end{array}$

are given on page 346 of Lawless, J.F., Statistical Models and Methods for Lifetime Data, 2nd ed., John Wiley & Sons, Inc., Hoboken, N.J., 2003. Conduct the log-rank test to compare the survivor functions for the two populations and report the appropriate p-value.
6.13 Three independent risks act on a population. The net lives, X_j, are exponential(λ_j), for [latex]j = 1, \, 2, \, 3[/latex]. Find
1. [latex]q_j (a, \, b)[/latex],
2. [latex]Q_j (a, \, b)[/latex],
3. π_j,
for [latex]j = 1, \, 2, \, 3[/latex].
6.14 A component can fail from one of two identifiable causes. Ken collects a large number of failures of both types and determined that

$\begin{array}{l} π_{1} = 0.73 π_{2} = 0.27 \end{array}$

and the crude lives have probability density functions

$\begin{array}{l} f_{Y_{1}} (t) = 1 0 \leq t \leq 1 \end{array}$

and

$\begin{array}{l} f_{Y_{2}} (t) = θ t^{θ - 1} 0 \leq t \leq 1 \end{array}$

for a positive parameter θ. Find the hazard functions of the net lives, X₁ and X₂, assuming that the risks are independent.
6.15 In a competing risks model, the distributions of the k crude lifetimes are exponential with identical parameter λ. In addition, the probabilities of failure from each of the risks (the [latex]\pi_{j}\mmlToken{mi}[mathvariant="normal"]{’} {s}[/latex]) are known. Assuming that the net lives are independent, find
1. the mean lifetime of the item,
2. the mean lifetime of the item if risk j is eliminated, for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].
6.16 Assume that the following are known in a competing risks model with two causes of failure:

$\begin{array}{l} π_{1} = \frac{1}{4} π_{2} = \frac{3}{4} S_{Y_{1}} (t) = e^{- α t} S_{Y_{2}} (t) = e^{- (λ t)^{κ}} \end{array}$

for [latex]t \ge 0[/latex]. Assuming that the risks are independent, find
1. the hazard function for the first net lifetime,
2. an expression for E[T],
3. an expression for the expected time to failure if risk 2 is removed.
The solutions to some parts of this problem might not be closed form.
6.17 If [latex]X_1, \, X_2, \, \ldots, \, X_k[/latex] are independent net lives and [latex]X_j \sim[/latex] exponential [latex](\lambda_j)[/latex] for [latex]j = 1, \, 2, \, \ldots, \, k[/latex], find [latex]\pi_j = P\big(X_j = \min \{X_1, \, X_2, \, \ldots, \, X_k \}\big)[/latex] for [latex]j = 1, \, 2, \, \ldots, \, k[/latex].
6.18 Beth considers independent net lives X₁ and X₂, where [latex]X_j \sim \hbox{Weibull}(\lambda_j, \, \kappa)[/latex] for [latex]j = 1, \, 2[/latex]. Find

$\begin{array}{l} π_{1} = P (X_{1} = min {X_{1}, X_{2}}) . \end{array}$
6.19 Rick uses a competing risks model with two independent risks C₁ and C₂. The net lifetime for risk 1 has a log logistic distribution with parameters λ₁ and [latex]\kappa_1[/latex]. The net lifetime for risk 2 has a log logistic distribution with parameters λ₂ and [latex]\kappa_2[/latex]. Write expressions for π₁ and π₂.
6.20 Let T be the lifetime of an item that is subject to three independent competing risks, for which the hazard functions for the crude lives are

$\begin{array}{l} h_{Y_{1}} (t) = \frac{a}{t + α} t \geq 0, \end{array}$

$\begin{array}{l} h_{Y_{2}} (t) = b t t \geq 0, \end{array}$

and

$\begin{array}{l} h_{Y_{3}} (t) = λ t \geq 0 \end{array}$

for positive parameters a, α, b, and λ. Given the values of π₁, π₂, and π₃, give an expression for the hazard function for the first net lifetime.
6.21 Consider a competing risks model with [latex]k = 2[/latex] independent risks. The first net lifetime, X₁, has a Weibull distribution with parameters λ₁ and [latex]\kappa_1[/latex]. The second net lifetime, X₂, has a Weibull distribution with parameters λ₂ and [latex]\kappa_2[/latex]. Find the expected remaining lifetime for an item that is operating at time t₀. Simplify your answer as much as possible.
6.22 Consider a competing risks model with [latex]k = 2[/latex] risks. Let X₁ be the net lifetime associated with risk 1 and let X₂ be the net lifetime associated with risk 2. The joint probability density function of X₁ and X₂ is

$\begin{array}{l} f (x_{1}, x_{2}) = 1 (x_{1}, x_{2}) \in A, \end{array}$

where A is the triangular region determined by connecting the points [latex](1, \, 2)[/latex], [latex](3, \, 2)[/latex], and [latex](3, \, 1)[/latex] in the [latex](x_1 , \, x_2 )[/latex] plane with lines.
1. Find π₁.
2. Find the survivor function of [latex]T = \min \{X_1, \, X_2 \}[/latex].
6.23 In a competing risks model with [latex]k = 2[/latex] independent risks, give an expression for [latex]Q_2 (a, \, b)[/latex], where both net lives have Weibull distributions, that is, X₁ has a Weibull distribution with parameters λ₁ and [latex]\kappa_1[/latex] and X₂ has a Weibull distribution with parameters λ₂ and [latex]\kappa_2[/latex]. Evaluate [latex]Q_2 (a, \, b)[/latex] to four decimal places when [latex]a = 1[/latex], [latex]b = 2[/latex], [latex]\lambda_1 = 3[/latex], [latex]\kappa_1 = 1 / 3[/latex], [latex]\lambda_2 = 4[/latex], and [latex]\kappa_2 = 1 / 4[/latex].
6.24 Consider the lifetime T having the bi-Weibull distribution with survivor function

$\begin{array}{l} S (t) = e^{- (λ_{1} t)^{κ_{1}} - (λ_{2} t)^{κ_{2}}} t \geq 0, \end{array}$

where λ₁, λ₂, [latex]\kappa_1[/latex], and [latex]\kappa_2[/latex] are positive parameters. The distribution has a bathtub-shaped hazard function if [latex]\min \{\kappa_1, \, \kappa_2\} < 1 < \max \{\kappa_1, \, \kappa_2\}[/latex]. Find the time value where [latex]h^\prime(t) = 0[/latex] for a bi-Weibull distribution with a bathtub-shaped hazard function.
6.25 Bonnie models the lifetime of an automobile using two dependent competing risks. The first risk is from accidents and the second risk is from all other causes. The joint survivor function of the two net lives associated with the two risks on their support is

$\begin{array}{l} S (x_{1}, x_{2}) = (1 - x_{1} / 2) (1 - x_{2} / 2) (1 + x_{1}^{2} x_{2} / 8) 0 < x_{1} < 2, 0 < x_{2} < 2, \end{array}$

where x₁ and x₂ are the odometer readings measured in hundreds of thousands of miles.
1. Find the marginal survivor function for X₁.
2. Find the joint probability density function of the net lifetimes.
3. Find π₂.
4. Find [latex]Q_2(0.5, \, 1.2)[/latex].
5. Find the expected lifetime of the automobile.
6. Perform a Monte Carlo experiment to support your solution to part (e).
6.26 The formula for the hazard function of the ith net life in a competing risks model is

$\begin{array}{l} h_{X_{i}} (t) = \frac{1}{S (t, t, \dots, t)} {[\frac{- \partial S (x_{1}, x_{2}, \dots, x_{k})}{\partial x_{i}}]}_{x_{1} = x_{2} = \dots = x_{k} = t} \end{array}$

for [latex]t \ge 0[/latex] and [latex]i = 1, \, 2, \, \ldots, \, k[/latex]. Find [latex]h_{X_1}(t)[/latex] for [latex]k = 2[/latex] risks and joint survivor function

$\begin{array}{l} S (x_{1}, x_{2}) = e^{- λ_{1} x_{1} - λ_{2} x_{2} - λ_{3} x_{1} x_{2}} x_{1} \geq 0, x_{2} \geq 0, \end{array}$

for [latex]\lambda_1 > 0[/latex], [latex]\lambda_2 > 0[/latex], and [latex]\lambda_3 > 0[/latex].
6.27 An item is subject to three competing risks with the associated three independent net lifetimes: [latex]X_1 \sim \hbox{Weibull}(1, \, 2)[/latex], [latex]X_2 \sim \hbox{exponential}(1)[/latex], and [latex]X_3 \sim \hbox{Weibull}(1, \, 3)[/latex]. Write computer code in a language of your choice to provide the numerical methods necessary to compute
1. the mean time to failure of the item,
2. the mean time to failure of the item with each of the risks eliminated individually.
In addition, calculate the mean of each net lifetime and provide a plausible explanation of why the net lifetime with the largest mean corresponds to the risk that has the greatest impact on E[T] when it is eliminated.
6.28 An item can fail from one of two competing risks. The first net lifetime is associated with accidents and is modeled by [latex]X_1 \sim \hbox{exponential}(\lambda)[/latex]. The second net lifetime is associated with wear out and is modeled by the random variable X₂ with hazard function

$\begin{array}{l} h_{X_{2}} (t) = β t t \geq 0, \end{array}$

for [latex]\beta > 0[/latex]. The net lifetimes are independent random variables.
1. Give an expression for the mean time to failure of the item; that is, find E[T], where [latex]T = \min\left\{ X_1, \, X_2 \right\}[/latex]. This expression will not be in closed form.
2. Give an expression for π₁. This expression will also not be in closed form.
3. Use numerical methods to calculate the two quantities given in parts (a) and (b) to seven digits when [latex]\lambda = 2[/latex] and [latex]\beta = 1[/latex].
4. Use Monte Carlo simulation to support your solutions in part (c).
6.29 A repairable item with negligible repair time fails according to a Poisson process with rate [latex]\lambda = 0.001[/latex] failures per hour. Find the probability of two or fewer failures between 3000 and 6000 hours.
6.30 A repairable item with negligible repair time fails according to a renewal process with interfailure time having the gamma distribution with parameters λ and [latex]\kappa[/latex]. Find the probability of n or fewer failures between times 0 and c.
6.31 Verify that the derivative of the renewal equation is satisfied when the items in a socket model have exponential lifetimes.
6.32 Consider a renewal process for which the times between failures have the Weibull distribution with scale parameter λ and shape parameter [latex]\kappa[/latex]. Find the expected value and population variance of the time of failure n for [latex]n = 1, \, 2, \, \ldots[/latex].
6.33 A repairable item with negligible repair time fails according to a nonhomogeneous Poisson process with intensity function [latex]\lambda (t) = 0.001 + 0.000001t[/latex] failures per hour, for [latex]t > 0[/latex]. Find the probability of two or fewer failures between 3000 and 6000 hours.
6.34 For a nonhomogeneous Poisson process with power law intensity function

$\begin{array}{l} λ (t) = λ κ (λ t)^{κ - 1} t > 0, \end{array}$

find the probability mass function for the number of events between times a and b.
6.35 Consider an age replacement policy model for which items are replaced at failure or at time c, whichever comes first. Assuming that the time to failure has the Pareto distribution with parameters λ and [latex]\kappa[/latex], find the expected number of failures by time b. Assume that [latex]\lambda \ll c \ll b[/latex].
6.36 Two different maintenance procedures are to be compared for a repairable itemml: age replacement and block replacement. Assume that the item has a lifetime that is a mixture of three distributions: a Weibull distribution with [latex]\lambda = 0.01[/latex] and [latex]\kappa = 0.6[/latex] (with [latex]p_1 = 0.05[/latex]), an exponential distribution with [latex]\lambda = 0.002[/latex] (with [latex]p_2 = 0.45[/latex]), and a Weibull distribution with [latex]\lambda = 0.001[/latex] and [latex]\kappa = 3.0[/latex] (with [latex]p_3 = 0.50[/latex]). Assume that time is measured in hours.
1. Calculate the theoretical mean lifetime of the item.
2. Use Monte Carlo simulation to compare the age replacement and block replacement maintenance strategies for the item with [latex]c = 1000[/latex] hours.
6.37 Georgie drives a car whose failure times are governed by a nonhomogeneous Poisson process with power law cumulative intensity function

$\begin{array}{l} Λ (t) = (λ t)^{κ} t > 0, \end{array}$

where t is measured in miles. If the car has 100,000 miles on the odometer, find the probability that Georgie can make a 1000-mile trip without a failure.
6.38 Bedrock Motors, Inc. is introducing their new “Tyrano-Taurus Rex” automobile, complete with a three-year warranty. Each Rex has a failure mechanism governed by a nonhomogeneous Poisson process with power law intensity function

$\begin{array}{l} λ (t) = λ^{κ} κ t^{κ - 1} t > 0, \end{array}$

where t is time (in years), and λ and [latex]\kappa[/latex] are positive parameters. If Fred, Wilma, Barney, and Betty each buy a Rex, find the expected number of failures under warranty that Bedrock Motors will experience for these four Rexes.
6.39 Cynthia is going camping. She takes along a flashlight which requires two batteries in order to operate. Cynthia’s batteries each have an exponential time to failure with a mean of [latex]1 / \lambda[/latex]. If Cynthia takes five batteries with her (two batteries in the flashlight and three spare batteries), what is the distribution of time that she will be able to use her flashlight? You may assume that (a) her battery replacement time is negligible, (b) her flashlight bulb never fails, and (c) she has a battery tester that allows her to determine which of the two batteries in the flashlight has failed. Write a short paragraph on the reasonableness of the assumption of exponential battery lifetimes.
6.40 The event times [latex]T_1, \, T_2, \, \ldots[/latex] in a nonhomogeneous Poisson process with cumulative intensity function [latex]\Lambda(t)[/latex] can be simulated with

$\begin{array}{l} T_{i} = Λ^{- 1} (E_{i}) \end{array}$ for [latex]i = 1, \, 2, \, \ldots[/latex], where [latex]E_1, \, E_2, \, \ldots[/latex] are the event times in a unit homogeneous Poisson process. Use this result to simulate the event times in a nonhomogeneous Poisson process with cumulative intensity function [latex]\Lambda(t) = t ^ 2[/latex] for [latex]0 < t < 2[/latex]. Provide convincing numerical evidence that you have correctly implemented the algorithm by conducting a Monte Carlo simulation experiment to estimate the number of events that have occurred by time [latex]t = 1.5[/latex].
6.41 Consider a nonhomogeneous Poisson process with intensity function [latex]\lambda(t)[/latex] and cumulative intensity function [latex]\Lambda(t)[/latex] defined on the time interval [latex]0 < t < s[/latex], where s is a prescribed, fixed, positive real number. Define the scaled intensity function as

$\begin{array}{l} λ^{⋆} (t) = \frac{λ (t)}{Λ (s)} 0 < t < s . \end{array}$
1. Show that [latex]\displaystyle{\int_0^s \lambda ^ \star (t) \, dt = 1}[/latex].
2. Find the functional forms of [latex]\lambda^\star (t)[/latex] for the following intensity functions:
  - [latex]\lambda(t) = \lambda[/latex]for [latex]0 < t < s[/latex],
  - [latex]\lambda(t) = \kappa \lambda ^ \kappa t ^ {\kappa - 1}[/latex] for [latex]0 < t < s[/latex],
  - [latex]\lambda(t) = \frac{\lambda \kappa ( \lambda t ) ^ {\kappa - 1}} {1 + ( \lambda t ) ^ \kappa}[/latex] for [latex]0 < t < s[/latex],
  for positive parameters λ and [latex]\kappa[/latex].
6.42 Barbara models the failure times of a digital camera by a nonhomogeneous Poisson process. Previous data has revealed that the intensity function for the times of warranty claims is well-modeled by the intensity function

$\begin{array}{l} λ (t) = 0.124 t t > 0, \end{array}$

where time is measured in years. The camera company is considering offering three consecutive one-year term warranties: one upon purchase of the camera, a second after one year of use, and the third after two years of use. In order to be competitive, the camera company has decided to make no profit on their warranty policies. Give the three revenue-neutral premiums that a customer has to pay for these warranties. Make the following assumptions to make your calculations simpler.
- Each repair costs exactly $100.
- A repair is instantaneous.
- Ignore the effect of the time value of money.
- Each repair is a minimal repair in the sense that the repair to the camera does not reset the intensity function to [latex]t = 0[/latex] but rather the camera’s age and intensity function are unaltered by the repair.
6.43 A truck requires a particular nonrepairable electrical component that has an exponential lifetime with a positive failure rate λ failures per hour. A site supports a large fleet of n trucks, each operating 24 hours a day, 7 days a week. A parts manager can make an order for spare parts once a week. Assuming that the lead time is 0 (that is, immediate delivery), what is the minimum number of parts that should be ordered up to each week to ensure that there is a probability of at least 0.9999 that a truck is not down for lack of this particular nonrepairable electrical component?
1. Write a paragraph describing an algorithm that the parts manager should select an order quantity.
2. Apply the algorithm from part (a) for [latex]n = 20[/latex] trucks and [latex]\lambda = 0.001[/latex] failures per hour.
3. Support your solution to part (b) via Monte Carlo simulation.
6.44 Natasha models power failures in the state of Virginia during the month of March with a Poisson process with rate [latex]\lambda = 7[/latex] failures per month. Given that there have been a total of 4 failures during the first 10 days of March, what is the probability that Virginia will have more than 12 power outages during the entire month of March?
6.45 The number of annual failures of a particular brand of carburetor is [latex]X_1 \sim \hbox{Poisson} (\lambda_1)[/latex]. The number of annual failures of a second brand of carburetor is [latex]X_2 \sim \hbox{Poisson} (\lambda_2)[/latex]. Assuming that the number of annual failures of the two types of carburetors are independent and that there are n annual failures observed for both types of carburetors (that is, [latex]X_1 + X_2 = n[/latex]), what is the probability distribution of the number of failures of the first carburetor during that particular year?
6.46 Which repairable system described below is the best candidate for being an improving system?
1. Automobile.
2. Wooden chair.
3. Blender.
4. Operating system.
5. Lawn mower.
6.47 Consider the three-component series system of repairable components with four cold-standby spares depicted below. All components are identical with failure rates 0.005 failure per hour. In this particular system, the failure detection and switching times are negligible. There is a repair facility with two repairmen. The repair rate is 0.01 repair per hour, and only one repairman can work on a failed component at a time. Find the expected time to system failure (that is, the expected time when there are fewer than three operating components) assuming all components are new at [latex]t = 0[/latex].

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Statistical Modeling: Regression, Survival Analysis, and Time Series Analysis Copyright © by Lawrence M. Leemis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Chapter 6 Topics in Survival Analysis

6.1 Nonparametric Methods

6.1.1 Survivor Function Estimation for Complete Data Sets

6.1.2 Survivor Function Estimation for Right-Censored Data Sets

6.1.3 Comparing Two Survivor Functions

6.2 Competing Risks

6.2.1 Net Lifetimes

6.2.2 Crude Lifetimes

6.2.3 General Case

6.3 Point Processes

6.3.1 Poisson Processes

6.3.2 Renewal Processes

6.3.3 Nonhomogeneous Poisson Processes

6.4 Exercises

License

Share This Book