Chapter 8 Time Series Modeling
This chapter presents several popular probability models for describing a time series, along with the associated statistical methods. Analogous to using the univariate normal distribution to model a quantitative variable which has a bell-shaped probability distribution, no time series model will provide a perfect fit to the data. The goal is to identify a probability model which provides a reasonable approximation to the time series, fit the model to an observed time series, and then use the fitted model for statistical inference, which is often forecasting.
8.1 Probability Models
A suite of probability models for time series known as linear models are introduced in this section. The unifying characteristic of these models is that they express the current value of the time series as a linear function of (a) the current noise term, (b) previous noise terms, and (c) previous values of the time series. We begin by taking a birds-eye view of these linear time series models by introducing general linear models (often abbreviated glm) and some of their properties. This is followed by a section that introduces a suite of time series models that are special cases of general linear models that are known as ARMA (autoregressive moving average) models. ARMA models are parsimonious in the sense that they are able to specify a wide variety of underlying probability models that govern a stationary time series with only a few parameters. With both general linear models and ARMA models, you will see a great deal of symmetry and some mathematics that works out beautifully on the road to developing time series models that can be implemented in real-world applications.
8.1.1 General Linear Models
General linear models provide an important way of thinking about how to define a time series model in a simple and general manner. Working with general linear models also provides some practice with using the backshift operator B, which was defined in Section 7.3.1. We also consider the causal and invertible form of general linear models. The causal form is important for establishing stationarity. The invertible form is important for ensuring a one-to-one relationship between parameter values and the associated population autocorrelation function.
The concepts of white noise from Definition 7.1 and linear filters from Section 7.3.1 are tied together in this section to define general linear models. White noise is a time series of mutually independent random variables denoted by [latex]\left\{ Z_t \right\}[/latex]. Each element in the white noise time series has common population mean 0 and common population variance [latex]\sigma _Z ^ {\, 2}[/latex]. Time series analysts often refer to the Zt values as random shocks whose purpose is to inject randomness into a time series model. Without these shocks, the time series model would be purely deterministic. Linear filters are a general way of expressing one time series as a linear combination of the values in another time series. White noise and linear filters are the key concepts in the definition of general linear models. As you will see in the next paragraph, there are two distinctly different ways of defining general linear models.
More specifically, one way to describe a general linear model is to define the current value in the time series Xt as the current white noise term Zt plus a linear combination of the previous white noise terms:
where the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] in the infinite series are real-valued constants. This time series model is stationary when appropriate restrictions are placed on the [latex]\psi_1, \, \psi_2, \, \ldots[/latex] values. Since this description of a general linear model is valid at time t, it is also valid at other time values, for example,
or
Solving these equations for the current white noise value and sequentially substituting into the first formulation of the general linear model, you can see that there is a second way to formulate a general linear model:
where the coefficients [latex]\pi_1, \, \pi_2, \, \ldots[/latex] are real-valued constants and appropriate restrictions are placed on the [latex]\pi_1, \, \pi_2, \, \ldots[/latex] values in order to achieve stationarity. In this second formulation of a general linear model, the current value of the time series is a linear combination of the previous values of the time series plus the current white noise term. This formulation is analogous to that of a multiple linear regression model with an infinite number of predictor variables.
A reasonable question to ask at this point is why there is no coefficient associated with Zt in both formulations of the general linear model. Although some authors associate a coefficient ψ0 with Zt, we avoid this practice and simply assume that [latex]\psi_0 = 1[/latex]. Including a ψ0 parameter is redundant because a nonzero constant multiplied by a white noise term is still a white noise term. The population variance of the white noise [latex]\sigma _Z ^ {\, 2}[/latex] is essentially absorbed into the ψ0 parameter. Also, some authors use a – rather than a + between terms on the right-hand side of the second formulation of the general linear model.
The two formulations for the general linear model involve a random variable on the left-hand side of the model and random variables on the right-hand side of the model. In some settings, this might be viewed as a transformation of random variables, but this is not the correct interpretation of the model in the time series setting. The general linear model formulations define a hypothesized relationship between the random variable on the left-hand side of the model and the random variables on the right-hand side of the model. In the first formulation of the general linear model, the current value of the time series Xt is hypothesized to be a linear combination of the current and previous noise values. In the second formulation of the general linear model, the current value of the time series Xt is hypothesized to be a linear combination of the previous values in the time series plus a noise term. This probability model is hypothesized to govern the process over time. The goal in constructing a time series model is to write a formula for a model which adequately captures the probabilistic relationship that governs the time series. Estimation of the model parameters will be followed by assessments to see if the model holds in an empirical sense.
The coefficients in the two formulations of a general linear model are related. To make these two formulations of the general linear model more concrete, we will now look at a specific instance.
A sleight of hand has occurred in the previous example with respect to the use of the backshift operator B, first as an operator and then as a variable. This paragraph concerns that dual use. When B is used as an operator, it has a domain or input, for instance, Xt, and a range or output, for instance, [latex]B X_t = X_{t - 1}[/latex]. In this case, the effect of the operator B on a time series value is to go back in the time series one unit of time. The input to B is the value of the time series at time t, and the output from B is the value of the time series at time [latex]t - 1[/latex]. The full domain of the operator B is the entire sequence of time series values. Why is it acceptable to take an operator like the backshift operator B and use it as a variable? It can be demonstrated that the backshift operator B functions like a linear map in the sense of allowing the standard multiplication and addition operations in its domain. In addition to the standard operations such addition, multiplication, and inversion, we may thus treat polynomials in B as polynomials in real variables.
For the particular case of the general linear model considered in the previous example, there was a relationship between the coefficients in the two formulations of the general linear model. We now consider whether there is a relationship between the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] and [latex]\pi_1, \, \pi_2, \, \ldots[/latex] in the general setting. We continue with our use of the backshift operator B. The first formulation of the general linear model is
which can be rewritten using the backshift operator as
or
The polynomial in B in this formulation of the model is denoted by [latex]\psi(B)[/latex], so the first formulation of the general linear model can be written compactly as
where [latex]\psi(B) = 1 + \psi_1 B + \psi_2 B ^ 2 + \cdots[/latex].
Now consider the second formulation of the general linear model:
Separating the time series terms on the left-hand side of the equation and the white noise term on the right-hand side of the equation results in
which can be rewritten using the backshift operator as
or
The polynomial in B in this formulation of the model is denoted by [latex]\pi(B)[/latex], so the second formulation of the general linear model can be written compactly as
where [latex]\pi(B) = 1 - \pi_1 B - \pi_2 B ^ 2 - \cdots[/latex].
Definition 8.1 gives the two formulations of the general linear model expressed in purely algebraic form and in terms of polynomials in the backshift operator.
In the previous example, we were able to perform algebraic steps to determine the relationship between the coefficients in the first formulation of the general linear model (that is, [latex]\psi_1, \, \psi_2, \, \ldots[/latex]) and the coefficients in the second formulation (that is, [latex]\pi_1, \, \pi_2, \, \ldots[/latex]). This can also be done in the more general setting. The equations that define the two formulations of the general linear model in Definition 8.1 written in terms of the backshift operator are
Applying the [latex]\psi(B)[/latex] polynomial to both sides of the second equation gives
or
or
for nonzero Xt. Since the product of the polynomials [latex]\psi(B)[/latex] and [latex]\pi(B)[/latex] is one, they are inverses. For suitable values of the coefficients, this allows us to calculate the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] from the coefficients [latex]\pi_1, \, \pi_2, \, \ldots[/latex] and vice versa. The inverse relationship between [latex]\psi(B)[/latex] and [latex]\pi(B)[/latex] will now be confirmed for the polynomials identified in the previous example.
The previous discussion constitutes a proof of the following theorem concerning writing the two forms of the general linear model in terms of polynomials in the backshift operator and the relationship between the two polynomials [latex]\psi(B)[/latex] and [latex]\pi(B)[/latex].
We will toggle between the purely algebraic formulations of the general linear model and the associated formulations using the backshift operator B based on which is more convenient and effective for the mathematics in a particular setting. Definition 8.1 gives two different ways of writing a general linear model, but is vague concerning any constraints placed on the coefficients. Some constraints on the coefficients that give the general linear model certain important characteristics are outlined next. Stationarity will play a central role in these constraints. The stationarity property implies that the time series is stable over time; this stability allows us to predict how the time series will behave in the future.
Causality and Invertibility
The general linear model is formulated in two different fashions in Definition 8.1. But we have not yet defined any general constraints on the coefficients in the two different formulations of the general linear model. We begin the consideration of appropriate constraints on the coefficients with some calculations on the first formulation of the general linear model.
The first formulation of the general linear model from Definition 8.1 using the purely algebraic form is
We would like to determine constraints on the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] that will result in a stationary model and also find expressions for quantities associated with the stationary version of this model, such as [latex]E \left[ X_t \right][/latex], [latex]V \left[ X_t \right][/latex], [latex]\gamma(k)[/latex], and [latex]\rho(k)[/latex]. Taking the expected value of both sides of the defining formula results in
because each of the white noise terms has expected value 0. This is a promising first step toward achieving stationarity. So far, no constraints are needed on the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex]. That will change when we compute the population variance of Xt. Taking the population variance of both sides of the defining formula results in
because the white noise terms are mutually independent random variables with common finite population variance [latex]\sigma _ Z ^ {\, 2}[/latex] (see Definition 7.1). Not all values of [latex]\psi_1, \, \psi_2, \, \ldots[/latex] will result in a finite population variance of Xt. Setting [latex]{\psi _ 1 = \psi _ 2 = \cdots = 1}[/latex], for example, results in an infinite population variance of Xt. In order to get a finite population variance, the ψ values must decrease in magnitude rapidly enough so that
One way to achieve this condition is to have finite values for the first q coefficients [latex]\psi_1, \, \psi_2, \, \ldots , \, \psi_q[/latex] then zeros thereafter. Any general linear model of the first formulation with coefficients that “cut off” in this fashion will satisfy the constraint. Another way of considering this constraint is to write this model using the backshift operator. Using Definition 8.1, the first formulation of the general linear model is
The polynomial in the backshift operator
will be considered for B values that can assume complex values. So B can have the form [latex]B = a + bi[/latex]. The constraint on the coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] is equivalent to [latex]\psi(B)[/latex] converging for all B values falling on or inside the unit circle. In other words, [latex]|B| \le 1[/latex].
The population autocovariance function for the general linear model stated in the form
with coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] satisfying the constraint can be calculated by using the definition of the population covariance:
for [latex]k = 1, \, 2, \, \ldots[/latex] because of the mutual independence of the terms in the white noise time series. As expected from the previous derivation, the autocovariance at lag 0 is the population variance of Xt:
where ψ0, the coefficient of Zt, equals 1. The associated autocorrelation function is
for [latex]k = 1, \, 2, \, \ldots[/latex]. Notice that [latex]\rho(0) = 1[/latex] as expected.
The derivation so far has been general, so when specific values of the coefficients [latex]\psi_1, \, \psi_2 , \, \ldots[/latex] are specified, we now have formulas to determine the population autocovariance function and the population autocorrelation function. Computing these two functions will be illustrated in the next example.
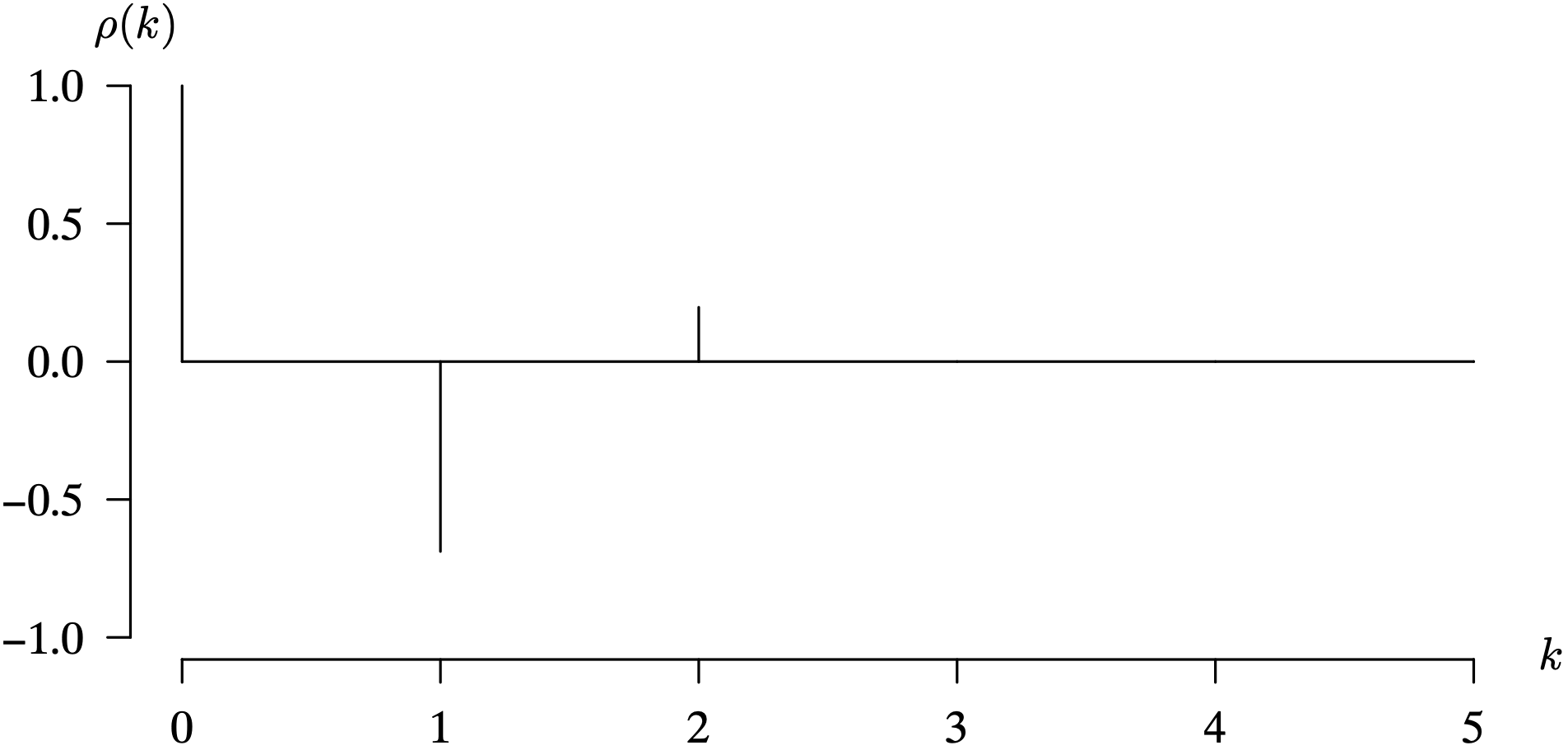
The constraint that has been placed on the values of [latex]\psi_1, \, \psi_2, \, \ldots[/latex] can be formalized in this definition of the causal representation of the general linear model.
The next example illustrates how to convert a general linear model into the causal form in order to establish stationarity.
When the second formulation of the general linear model that uses the coefficients [latex]\pi_1, \, \pi_2, \, \ldots[/latex] is used, there is an analogous property known as invertibility which is defined next. In this case the coefficients [latex]\pi_1, \, \pi_2, \, \ldots[/latex] need to decrease in magnitude rapidly enough so that
Loosely speaking, a time series model is invertible if there is a one-to-one correspondence between the coefficients [latex]\pi_1, \, \pi_2, \, \ldots[/latex] and the associated population autocorrelation function.
So causality and invertibility are dual properties. Causality indicates that a time series model can be written in the first formulation of the general linear model from Definition 8.1 with coefficients that result in a stationarity model. Invertibility indicates that a time series model can be written in the second formulation of the general linear model from Definition 8.1 with coefficients that ensure a one-to-one correspondence between the coefficients and the population autocorrelation function.
There are three unsettling aspects to the general linear model. First, it only considers linear relationships between the X‘s and the Z‘s. Situations might arise in which a quadratic term, for example, might be appropriate. Second, the general linear model has an infinite number of parameters: the coefficients [latex]\psi_1 , \, \psi_2, \, \ldots[/latex] for the first formulation and the coefficients [latex]\pi_1 , \, \pi_2, \, \ldots[/latex] for the second formulation. ARMA (autoregressive moving average) models, which are special cases of general linear models that are introduced in the next section, limit the number of parameters in the model. The third shortcoming concerns the population mean. Taking the expected value of both sides of the first formulation of the general linear model
for example, gives [latex]E \left[ X_t \right] = 0[/latex]. But the vast majority of real-world time series are not centered around zero. These problems associated with an infinite number of parameters and nonzero mean value will be overcome by the ARMA models introduced in the next section.
8.1.2 An Introduction to ARMA Models
The autoregressive moving average time series model, universally known as the ARMA model, provides two twists on the general linear model. First, the ARMA model limits the number of terms, and therefore limits the number of parameters. Second, the ARMA model includes both types of terms in the two formulations of the general linear model given in Definition 8.1.
There are several reasons for the popularity of the ARMA time series model. First, the population autocorrelation function [latex]\rho(k)[/latex] for an ARMA model can take on a wide variety of shapes, which makes it an appropriate time series model in a wide variety of applications. Second, the ARMA model is parsimonious in the sense that it typically requires only a small number of parameters to achieve an adequate representation of the probability model governing a time series. The notion of parsimony appears in all branches of statistics in which there is interest in finding an approximate probability model using the smallest number of parameters. Third, the ARMA model has been around for several decades, which means that dozens of software packages have been developed over the years for model identification, parameter estimation, forecasting, etc. Although the emphasis here will be on the R language, there are many other software packages that support time series modeling.
The general linear model from Definition 8.1 used the parameters [latex]\psi_1 , \, \psi_2, \, \ldots[/latex] for the first formulation and [latex]\pi_1 , \, \pi_2, \, \ldots[/latex] for the second formulation. Of course both of these formulations have the additional parameter [latex]\sigma _ Z ^ {\, 2}[/latex], which is the population variance of the white noise. Tradition dictates that in the conversion from the first formulation of the general linear model to the ARMA model, the Greek letter [latex]\psi[/latex] used for coefficients in the general linear model is replaced by [latex]\theta[/latex], and there are q of these coefficients: [latex]\theta_1 , \, \theta_2 , \, \ldots , \, \theta_q[/latex]. Likewise, in the conversion from the second formulation of the general linear model to the ARMA model, the Greek letter π used for the coefficients in the general model is replaced by [latex]\phi[/latex], and there are p of these coefficients: [latex]\phi_1 , \, \phi_2 , \, \ldots , \, \phi_p[/latex].
So two key parameters in specifying an ARMA model are p and q, which are both nonnegative integers. The parameter p is the number of coefficient parameters in the autoregressive portion of the model; the parameter q is the number of coefficient parameters in the moving average portion of the model. The format for specifying the orders p and q of an ARMA model with p autoregressive terms and q moving average terms is ARMA([latex]p, \, q)[/latex].
The autoregressive portion of this time series model is aptly named because the current value of the time series Xt is regressed on the p previous values of itself. White noise is injected into the model through [latex]\left\{ Z_t \right\}[/latex] because it is the widest class of the three noise processes from Definition 7.1 which gives the probabilistic properties that are derived in this chapter.
If an ARMA model only involves, for example, the autoregressive portion of the model with two terms (that is, no moving average terms because [latex]\theta_1 = \theta_2 = \cdots = \theta_q = 0[/latex]), then this ARMA([latex]2, \, 0[/latex]) model is specified as an AR(2) model. Likewise, if an ARMA model only involves, for example, the moving average portion of the model with four terms (that is, no autoregressive terms because [latex]\phi_1 = \phi_2 = \cdots = \phi_p = 0[/latex]), then this ARMA([latex]0, \, 4[/latex]) model is specified as an MA(4) model. An ARMA([latex]0, \, 0[/latex]) model is just a time series of white noise, which was analyzed in Examples 7.9 and 7.15.
The ARMA([latex]p, \, q[/latex]) time series model from Definition 8.4 can also be written in terms of the backshift operator B. Taking the original form of the ARMA([latex]p, \, q[/latex]) model
and separating the autoregressive terms on the left-hand side of the equation and the moving average terms on the right-hand side of the equation results in
This can be written in terms of the backshift operator as
or
or more compactly as
where the polynomials in B are
and
and these are often referred to as the characteristic polynomials. This algebra constitutes a proof of the alternative representation of the ARMA([latex]p, \, q[/latex]) time series model using polynomials.
Being able to convert between the purely algebraic formulation of an ARMA([latex]p, \, q[/latex]) model and the backshift operator formulation is an important skill in time series analysis. The next three examples illustrate how to perform these conversions.
The previous example converted an ARMA time series model from a purely algebraic formulation to a formulation that uses the backshift operator. The next example goes in the other direction.
The third and final example of converting between the purely algebraic formulation and backshift formulation of the ARMA([latex]p, \, q[/latex]) model would certainly be classified as a trick question. The example emphasizes the importance of looking for common factors between the [latex]\phi(B)[/latex] and [latex]\theta(B)[/latex] polynomials.
Based on this example involving a common factor in the [latex]\phi(B)[/latex] and [latex]\theta(B)[/latex] polynomials, we will henceforth assume that the modeler has removed any redundant factors in an ARMA([latex]p, \, q[/latex]) time series model. So any ARMA([latex]p, \, q[/latex]) model you see going forward will in this sense be presented in lowest terms with no common factors between [latex]\phi(B)[/latex] and [latex]\theta(B)[/latex].
Since an AR(p) model has a finite number of coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] in the autoregressive portion of the model, they always satisfy
so AR(p) models are always invertible per Definition 8.3. Likewise, since an MA(q) model has a finite number of coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex] in the moving average portion of the model, they always satisfy
so MA(q) models are always stationary per Definition 8.2. In an advanced class in time series, you will prove that an AR(p) model is stationary when all of the p complex roots of the polynomial [latex]\phi(B) = 0[/latex] lie outside of the unit circle in the complex plane. Likewise, an MA(q) model is invertible when all of the q complex roots of the polynomial [latex]\theta(B) = 0[/latex] lie outside of the unit circle in the complex plane. An ARMA([latex]p, \, q[/latex]) model is stationary when all of the p complex roots of [latex]\phi(B) = 0[/latex] lie outside of the unit circle in the complex plane. An ARMA([latex]p, \, q[/latex]) model is invertible when all of the q complex roots of [latex]\theta(B) = 0[/latex] lie outside of the unit circle in the complex plane. These results are summarized below.
We now revisit the first numeric example of a time series model that we encountered earlier in this chapter to check and see if it is both stationary and invertible.
We will get some further practice with these calculations involving the polynomials [latex]\phi(B)[/latex] and [latex]\theta(B)[/latex] when we investigate special cases of the ARMA([latex]p, \, q[/latex]) model in more detail in the sections that follow.
Shifted ARMA models
We now address a major shortcoming of the ARMA([latex]p, \, q[/latex]) model that–fortunately–is easily overcome. For a stationary ARMA([latex]p, \, q[/latex]) model as it has been defined in Definition 8.4, the expected value of Xt is [latex]E \left[ X_t \right] = 0[/latex]. But most real-world stationary time series are not centered about 0; they are typically centered about some nonzero constant value. The reason that we have waited this long to bring up the topic of a time series centered around a value other than zero is that when we shift the time series, there will be no change in the population autocovariance and autocorrelation functions because population covariance and correlation are unaffected by shifting the time series. The mathematics involved with determining these important functions is much cleaner if you assume that the time series model is centered about zero. There are two ways to tweak the ARMA([latex]p, \, q[/latex]) model to allow for it to be centered about some constant value. These two alterations are presented next.
The first way to introduce a nonzero central value for an ARMA([latex]p, \, q[/latex]) time series model is to subtract μ from all of the values in the time series. In other words, transform the usual ARMA([latex]p, \, q[/latex]) time series model
to the shifted ARMA([latex]p, \, q[/latex]) time series model
This can be written compactly in terms of the backshift operator B as
where [latex]\phi(B)[/latex] is the usual polynomial of degree p in B associated with the autoregressive portion of the model:
and [latex]\theta(B)[/latex] is the usual polynomial of degree q in B associated with the moving average portion of the model:
In this particular formulation of a shifted ARMA([latex]p, \, q[/latex]) model, the population mean of the process is [latex]E \left[ X_t \right] = \mu[/latex] when the model is stationary. This can be established by taking the expected value of both sides of the shifted ARMA([latex]p, \, q[/latex]) time series model.
A second way to formulate a shifted ARMA([latex]p, \, q[/latex]) time series model with a nonzero population mean is to simply add a constant, denoted by [latex]\tilde \mu[/latex], to the right-hand side of the model:
This can be written in terms of the backshift operator as
The reason that a tilde has been placed above μ in this formulation is that [latex]\tilde \mu[/latex] is not the population mean of the time series model. The two ways of formulating a shifted ARMA([latex]p, \, q[/latex]) time series model in these two fashions are summarized as follows.
The example that follows illustrates how to convert a shifted time series model from one of these forms to the other.
The previous example can be generalized from the shifted ARMA([latex]1, \, 1[/latex]) model to the shifted ARMA([latex]p, \, q[/latex]) model. The following theorem gives the relationship between μ and [latex]\tilde \mu[/latex] for the two formulations of the shifted ARMA([latex]p, \, q[/latex]) models in Definition 8.5.
In the previous example, the value of [latex]\mu = E \left[ X_t \right][/latex] could have been calculated by appealing to Theorem 8.4 with [latex]\tilde \mu = 8[/latex] and [latex]\phi_1 = 0.6[/latex], which gives
This provides an illustration of how Theorem 8.4 provides a mechanism for converting between the two forms of the shifted ARMA([latex]p, \, q[/latex]) models given in Definition 8.5.
This section has provided an introduction to linear models. The first subsection surveyed the two formulations of the general linear model and introduced the causality and invertibility properties. The second subsection introduced a special case of the general linear model known as the ARMA (autoregressive moving average) model. These time series models are inherently probabilistic in nature. The next section introduces some of the associated statistical topics in time series analysis: parameter estimation, forecasting, model assessment, and model selection.
8.2 Statistical Methods
The previous section introduced two linear probability models for time series: the general linear model and the ARMA model. These models contain parameters which can be used to tune the model to a particular application. This chapter introduces the statistical methods that are used to estimate these parameters and assess whether the model with its fitted parameters provides an adequate representation of the probabilistic mechanism governing the time series. As you read the rest of this book, you should be continually asking yourself whether the new material is associated with a probability model or presents a statistical method. The statistical methods are presented here in a somewhat generic manner; the specific implementations on a time series of observations occurs subsequently. The first subsection in this section introduces three methods for estimating the parameters in an ARMA model: the method of moments, least squares, and maximum likelihood. This is followed by a subsection that considers the important topic of forecasting future observations in a time series. Subsections on model assessment and model selection complete the section.
8.2.1 Parameter Estimation
The emphasis now shifts from a time series model, which is developed using probability theory, to statistical questions associated with a realization of a time series. The observed values of this realization are denoted by [latex]X_1, \, X_2, \, \ldots , \, X_n[/latex] when considered abstractly; when specific values are considered, they are denoted by [latex]x_1, \, x_2, \, \ldots , \, x_n[/latex].
Before considering parameter estimation, we consider the topic of model identification. Since p and q are nonnegative integers, there are an infinite number of ARMA([latex]p, \, q[/latex]) models from which to choose. Which model is appropriate for a particular application? Most statistical software packages that perform the analysis of a time series have functions that estimate parameters and forecast future values of the time series. So those two aspects of time series analysis are largely automated. The part of the process that requires some insight from the modeler is the specification of an appropriate time series model for a particular application. By what criteria do we decide whether an MA(1), AR(2), or ARMA([latex]2, \, 1[/latex]) is a tentative or a final time series model? The two steps associated with model identification for an ARMA([latex]p, \, q[/latex]) model are given next.
- Inspect the time series plot. The process of identifying a time series model always begins with a careful inspection of a plot of the time series. Take a few minutes to look for cyclic variation, trends, step changes, outliers, and nonconstant variance in the plot of the time series. Visually assess the time series for any serial correlation. The human eye can spot subtleties that an algorithm might miss. Only you can perform this step. We assume for now that no trends, step changes, outliers, cyclic variation, or nonconstant variance in the time series have been identified, so a stationary model for the time series is sought. Modeling cyclic variation, trends, and nonconstant variance will be taken up subsequently.
- Inspect the plots of rk and [latex]r_k^*[/latex]. Inspecting plots of the sample autocorrelation function and the sample partial autocorrelation function is an attempt to conduct a visual pattern match between the sample autocorrelation patterns with a known inventory of population autocorrelation patterns for the various ARMA([latex]p, \, q[/latex]. The minimum length of a time series in order to make meaningful visual comparisons between the sample and population autocorrelation functions is about [latex]n = 60[/latex] or [latex]n = 70[/latex] observations. As will be seen in subsequent chapters, the shape of the sample autocorrelation function and the sample partial autocorrelation function can provide clues as to an appropriate time series model. In some cases, the values of p and q in the ARMA([latex]p, \, q[/latex]) model become immediately apparent upon viewing these three plots. In other cases, the situation is murky, and there might be two or three potential ARMA([latex]p, \, q[/latex]) models that seem to be plausible. Since we have assumed that the time series is stationary in the previous paragraph, there is no need to transform or difference the data based on these plots in the current setting. The p and q values for the ARMA time series model identified from this step will be known as the tentative model. Once a tentative model has been identified, the next step is to estimate the parameters, which accounts for the remainder of this section.
We would like to estimate the parameters of a stationary and invertible tentative ARMA([latex]p, \, q[/latex]) model. It is assumed that the number of autoregressive terms p and the number of moving average terms q have been established for a tentative ARMA([latex]p, \, q[/latex]) time series model based on an inspection of the sample autocorrelation and sample partial autocorrelation functions. There are a total of [latex]p + q + 1[/latex] unknown parameters in a standard ARMA([latex]p, \, q[/latex]) model from Definition 8.4: the autoregressive coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], the moving average coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. The shifted ARMA([latex]p, \, q[/latex]) model from Definition 8.5 has the additional parameter μ.
Consistent with conventional notation in statistics, hats on unknown parameters denote their point estimators. The point estimator of the unknown parameter [latex]\phi_1[/latex], for example, is [latex]\hat \phi_1[/latex]. The point estimators developed here are random variables that take on one particular value for an observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. Point estimators are typically paired with a [latex]{100(1 - \alpha)}\%[/latex] confidence interval that gives a sense of the precision of the point estimator. A confidence interval for the unknown parameter [latex]\phi_1[/latex], for example, is typically expressed in the form [latex]L < \phi_1 < U[/latex], where L is the random lower bound of the confidence interval and U is the random upper bound of the confidence interval.
In most practical problems involving a time series model, a shifted ARMA([latex]p, \, q[/latex]) model is used because very few time series are centered around zero. Since the ARMA([latex]p, \, q[/latex]) time series model is generally assumed to be stationary and invertible, it is common practice in time series analysis to estimate the population mean parameter μ with the sample mean [latex]\bar X[/latex]. This is justified by the fact that [latex]E \left[ X_t \right] = \mu[/latex] for a stationary and invertible shifted ARMA([latex]p, \, q[/latex]) model. This is consistent with the method of moments approach. Once μ has been estimated, the new time series which is shifted by [latex]\hat{\mu} = \bar X[/latex] is
This time series can be fitted to a standard ARMA([latex]p, \, q[/latex]) model from Definition 8.4. This new time series has a sample mean value of zero because
So for now we dispatch with the parameter μ and assume that it will typically be estimated by [latex]\bar x[/latex] for a stationary and invertible ARMA([latex]p, \, q[/latex]) model by centering the time series as described above. Both the original time series and the centered time series will be denoted by as [latex]\left\{ X_t \right\}[/latex] or [latex]\left\{ x_t \right\}[/latex] in order to avoid introducing a new letter (Yt or yt) into the notation. The parameter estimation techniques that follow will be applied to a standard ARMA([latex]p, \, q[/latex]) model centered around zero, which assumes that μ has been estimated in the shifted model. This will make the notation somewhat more compact. The population variance of [latex]\bar X[/latex] for mutually independent and identically distributed observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] is the well-known formula
But for a stationary ARMA([latex]p, \, q[/latex]) time series model with population autocovariance function [latex]\gamma(k)[/latex] and population autocorrelation function [latex]\rho(k)[/latex], the population variance of the sample mean is
Notice that this formula collapses to [latex]V \big[ \bar X \big] = \sigma _ X ^ {\, 2} / n[/latex] when [latex]\rho(1) = \rho(2) = \cdots = \rho(n - 1) = 0[/latex] as expected. This formula should be kept in mind whenever statistical inferences, such as confidence intervals or hypothesis tests, are made concerning the population mean from a realization of a time series. The sample mean is a meaningful summary statistic for a time series only when appropriate transformations have been applied to the time series in order to reduce it to a stationary time series.
Three techniques for the estimation of parameters in a time series model will be introduced here: the method of moments, least squares, and maximum likelihood estimation. There are three reasons why just one parameter estimation technique is not adequate. First, an AR(3) model, for example, might be well fitted with one estimation technique, but an MA(2) model, on the other hand, might be more compatible with another estimation technique. Second, it is often the case that one technique will provide initial estimates for a numerical method associated with a second technique. Third, some of the estimation techniques provide estimators which have degraded statistical properties near the boundaries of the stationarity or invertibility regions. The three techniques will be discussed generally below, and then will be illustrated with examples subsequently using real time series data.
Method of Moments
The essence of the method of moments technique is to equate low-order population and sample moments and solve for all unknown parameters. This method was developed by English mathematician and biostatistician Karl Pearson. This approach often seems arresting to those encountering it for the first time because population moments are constants and sample moments are random variables. Equating constants and random variables is simply a device that is used to get a perfect match between low-order population and sample moments.
In a non-time-series context with data values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] and m unknown population parameters, the m equations
can be solved to arrive at the m method of moments estimators of the unknown parameters. In some settings this can be done analytically, but in other settings numerical methods are required.
Returning to a time-series context, the stationarity assumption (see Definition 7.6) places requirements on only the first two population moments [latex]E \left[ X_t \right][/latex] and [latex]E \left[ X _ t ^ 2 \right][/latex]. Stationarity places no requirements on the third and higher order moments. But stationarity does imply that the autocorrelation between two observations depends only on the lag, and this can be exploited to generate the necessary number of equations to employ the method of moments technique. Consider a stationary and invertible ARMA([latex]p, \, q[/latex]) model, for example, that has four unknown parameters. Solving the set of four equations in the four unknown parameters
yields the method of moments estimators for the four unknown parameters. The usual approach to fitting a time series model to a realization of a time series by the method of moments technique is to use the first two of these equations, and then equate population and sample autocorrelations at enough low-order lags in order to account for all unknown parameters. In this way the population and the sample autocorrelations will match at lower-order lags.
Least Squares Estimation
The least squares estimation technique is used nearly universally in regression analysis. This method developed by German mathematician Carl Friedrich Gauss. The essence of the least squares technique is to find the values of the unknown parameters that minimize the sum of squares of the error terms in a model. In the time series setting, we want to find the values of the parameters that minimize
The use of least squares for ARMA([latex]p, \, q[/latex]) models requires two steps. First, solve the target model for Zt, and then substitute that expression into the equation above. At this point, S is written in terms of the unknown parameters. Second, take the partial derivatives of S with respect to all unknown parameters and solve for the unknown parameters. The set of equations to solve is often referred to as the orthonormal equations. The solution to these equations yields the least squares estimates of the unknown parameters. In some cases these equations can be solved analytically; in other cases numerical methods are required.
Maximum Likelihood Estimation
Maximum likelihood estimation is the most prevalent technique for estimating unknown parameters from a data set in the field of statistics, particularly outside of regression. The method was popularized by English statistician Sir Ronald Fisher. The essence of the maximum likelihood estimation technique, whether applied in time series analysis or otherwise, is to select the parameters in a hypothesized model that are the most likely ones to have resulted in the observed data values. The maximum likelihood estimators of the unknown parameters are found by maximizing the likelihood function, which is the joint probability density function of the data values evaluated at their observed values. The likelihood function is a function of the unknown parameters in the model with the data values fixed at their observed values. We begin by using maximum likelihood estimation on an ARMA([latex]0, \, 0[/latex]) model in order to establish some of the issues associated with the use of the maximum likelihood estimation technique to estimate the parameters in a time series model.
Applying the maximum likelihood estimation technique to the ARMA([latex]0, \, 0[/latex]) time series model was ideal in that the point estimator for [latex]\sigma _ Z ^ {\, 2}[/latex] could be expressed in closed form and an exact two-sided confidence interval for [latex]\sigma _ Z ^ {\, 2}[/latex] could be derived to give an indication of the precision of the point estimator. There are three key take-aways from the ARMA([latex]0, \, 0[/latex]) example involving maximum likelihood estimation.
- We needed to narrow the assumption of white noise error terms to Gaussian white noise error terms in order to implement the maximum likelihood estimation technique.
- We were fortunate that the likelihood function could be factored into the product of the marginal probability density functions because of the mutual independence of the observations. This will not be the case with the ARMA([latex]p, \, q[/latex]) model with [latex]p > 0[/latex] and [latex]q > 0[/latex].
- We were fortunate in the sense that we could establish an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\sigma _Z ^ {\, 2}[/latex] based on a pivotal quantity. For ARMA([latex]p, \, q[/latex]) models with [latex]p > 0[/latex] and/or [latex]{q > 0}[/latex] we will generally have only approximate confidence intervals which are based on asymptotic results.
We now address the third take-away concerning confidence intervals for parameters in ARMA models that go beyond the ARMA([latex]0, \, 0[/latex]) model illustrated in the previous example. The mathematics associated with deriving the exact distribution of some pivotal quantity becomes too difficult once autocorrelation is injected into a model, so we use asymptotic results concerning the parameter estimates in order to arrive at approximate confidence intervals. To frame the conversation concerning these asymptotic results, some notation must be established. Let
$$
\beta = \left( \beta _ 1 , \, \beta _ 2 , \, \ldots ,
\, \beta _ r \right) ^ \prime
$$
be a vector that denotes the r unknown parameters in a time series model. In the case of a shifted ARMA([latex]p, \, q[/latex]) model, for example, the elements of β are the [latex]p + q + 2[/latex] unknown parameters [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex], [latex]\theta_1[/latex], [latex]\theta_2[/latex], [latex]\ldots[/latex], [latex]\theta_q[/latex], [latex]\mu[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex]. Let [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] denote a realization of the time series observations. The likelihood function is
and the associated log likelihood function is
The jth element of the score vector is
for [latex]j = 1, \, 2, \, \ldots, \, r[/latex]. Equating the elements of the score vector to zero and solving for the unknown parameters yields the maximum likelihood estimators [latex]\hat \beta _ 1, \, \hat \beta _ 2, \, \ldots , \, \hat \beta _ r[/latex]. The [latex](j, \, k)[/latex] element of the Fisher information matrix [latex]I(\beta)[/latex] is
for [latex]j = 1, \, 2, \, \ldots, \, r[/latex] and [latex]k = 1, \, 2, \, \ldots, \, r[/latex], when the expected values exist. The Fisher information matrix is estimated by the observed information matrix [latex]O\big( \hat \beta \big)[/latex], whose [latex](j, \, k)[/latex] element is
for [latex]j = 1, \, 2, \, \ldots, \, r[/latex] and [latex]k = 1, \, 2, \, \ldots, \, r[/latex]. The inverse of the observed information matrix is the asymptotic variance–covariance matrix of the parameter estimates. If one is willing to ignore the off-diagonal elements of this matrix, the square roots of the diagonal elements are estimates of the standard errors of the point estimators. The asymptotic normality of maximum likelihood estimators allows one to construct approximate confidence intervals for the unknown parameters.
We were able to obtain an exact two-sided confidence interval for [latex]\sigma _ Z ^ {\, 2}[/latex] for the ARMA([latex]0, \, 0[/latex]) model in the previous example; the next example goes through the appropriate steps for the model had we not been so lucky. We return to the analysis of the standard ARMA([latex]0, \, 0[/latex]) time series model because it is the only ARMA([latex]p, \, q[/latex]) model with a single unknown parameter and associated tractable mathematics.
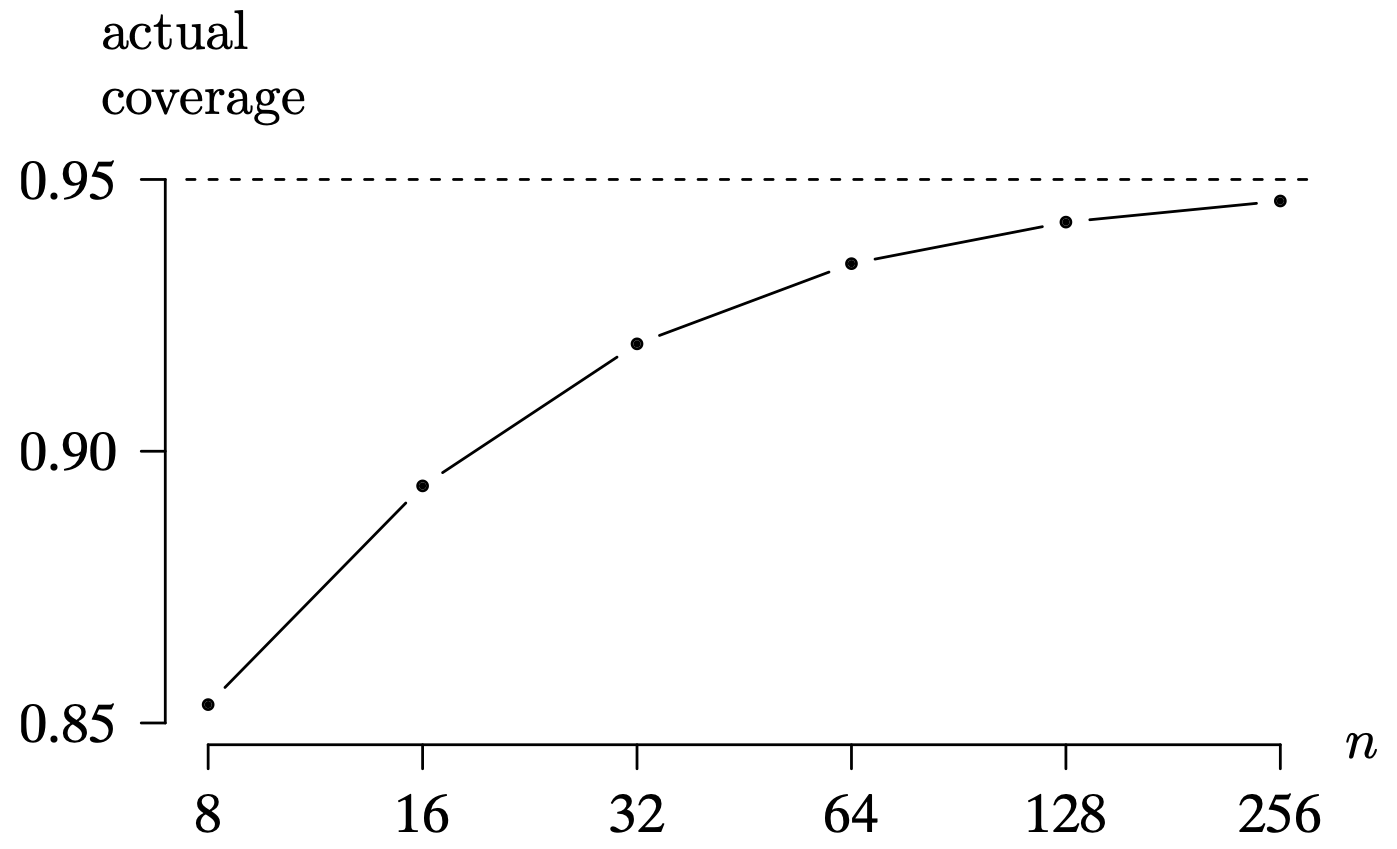
Long Description for Figure 8.3
The horizontal axis n ranges from 8 to 256 in multiples of 2. The vertical axis measures the actual coverage value and ranges from 0.85 to 0.95 in increments of 0.05. A dashed horizontal line is drawn at the actual coverage value of 0.95. A concave down curve passes through (8, 0.85), (16, 0.89), (32, 0.925), (64, 0.94), (128, 0.945), and (256, 0.947), all while approaching the dashed horizontal line. All data are estimated.
This ends the discussion of the important topic of parameter estimation. The time series model that emerges from this step is known as a fitted tentative model. Three techniques for parameter estimation have been introduced: the method of moments, least squares, and maximum likelihood estimation. In time series analysis, exact confidence intervals for the unknown parameters are typically mathematically intractable, so we must settle for asymptotically exact confidence intervals.
The next section introduces another important statistical topic that arises frequently in time series analysis: the prediction of future values in a time series based on a realization of n observations of a time series, which is typically known as forecasting.
8.2.2 Forecasting
The purpose of forecasting is to predict one or more future values of a time series based on observed values of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. Forecasting future values of a time series often plays a critical role in policy decisions. The closing price of the Dow Jones Industrial Average tomorrow, the number of oysters in the Chesapeake Bay next year, the high temperature in Tuscaloosa on Saturday, and a company’s profit next quarter are examples of applications of forecasting.
The term “forecasting” is synonymous with “prediction” and the two terms will be used interchangeably. Forecasting is a slightly more popular term in the time series literature. Both terms can be interpreted as “telling before.”
Forecasting involves extrapolation of the time series model outside of the time frame associated with the observed values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], typically into the future. The notion of backcasting, which is predicting values in the past, will not be considered here. Care must be taken to ensure that the fitted probability model still applies in the time range in which the extrapolation occurs. If future observations are governed by the same probability model as previous observations, then a forecasted value is meaningful. Furthermore, if an ARMA([latex]p, \, q[/latex]) model is used, it is subject to errors in identification (for example, the wrong values of p and q or perhaps an ARMA model is used when a non-ARMA model is appropriate) and estimation (for example, due to random sampling variability or choosing an inferior parameter estimation procedure).
There are several choices for forecasting notation. We assume that the values of a time series [latex]\left\{ X_t \right\}[/latex] are given by the observed values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. We would like to predict the value of the time series h (for “horizon”) time units into the future, given that we know the values of [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] and our forecast is being made at time n. The notation that we will use for this future value of the time series will be the random variable [latex]X_{n + h}[/latex]. Its associated predicted value will be denoted by [latex]\hat{X} _ {n + h}[/latex]. This predicted value is defined as the conditional expected value of the future value given the values of the n observed values:
We will use the alternative notation [latex]\hat{X} _ n (h)[/latex] for the forecast whenever there might be some ambiguity associated with the origin of the forecast. The default assumption for forecasting in this book is that we are making a forecast based on n observed values, and the forecast is being made at time origin n for h time units into the future. The forecasted value at time [latex]n + h[/latex] can be thought of as the average of all future possibilities given the history up to time n. But why use the conditional expectation? Might a quantile of the probability distribution of [latex]X_{n + h}[/latex], for example, the population median, provide a better forecast? The rationale behind using the conditional expectation is that it minimizes the mean square error of the predicted value, which is defined as
among all linear functions of the observed values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. For this reason, the forecasted value given by the conditional expectation is often known as the best linear predictor of [latex]X_{n + h}[/latex] in the sense of minimizing the mean square error of the predicted value.

Long Description for Figure 8.4
The horizontal axis t ranges from 1 to 7 in increments of 1 unit. The vertical axis x subscript t is unmarked. The observed points x 1, x 2, x 3, and x 4 are plotted at t values 1, 2, 3, and 4, respectively. Each is plotted a little above the other, and points are connected by lines. The forecasted values X cap 5, X cap 6, and X cap 7 are plotted as circles at t values 5, 6, and 7, respectively, forming an increasing trend. Dashed vertical lines are drawn at t values 5, 6, and 7. Bell-shaped curves are drawn on the vertical lines at t equals 5, 6, and 7 so that they have a peak to the right. As t increases, bell shaped curves are becoming wider.
Figure 8.4 illustrates the case of a (tiny) time series of just [latex]n = 4[/latex] observations: [latex]x_1, \, x_2, \, x_3, \, x_4[/latex]. (Recall that [latex]n = 60[/latex] or [latex]n = 70[/latex] is the minimum value of n in practice. This example with a tiny value of n is for illustrative purposes only.) The observed values of the time series are indicated by points which are connected by lines. Each of the three forecasted values, [latex]\hat{X}_5, \, \hat{X}_6, \, \hat{X}_7[/latex], is indicated by a [latex]\circ[/latex]. The three forecasts, associated with [latex]h = 1[/latex], [latex]h = 2[/latex], and [latex]h = 3[/latex], are made at time [latex]{t = n = 4}[/latex]. In addition, there are three probability density functions, each rotated clockwise 90°, which indicate the probability distributions of the random future observations [latex]X_5, \, X_6, \, X_7[/latex]. There are three key observations associated with this figure.
- The time series values [latex]x_1, \, x_2, \, x_3, \, x_4[/latex] increase over time, and the associated forecasted values [latex]\hat{X}_5, \, \hat{X}_6, \, \hat{X}_7[/latex] continue this trend.
- The population variance of the probability distributions of [latex]X_5, \, X_6, \, X_7[/latex] increases as the forecasting time horizon increases. This is consistent with weather prediction, for example, in that the weather prediction three days from now is less precise than the weather prediction tomorrow.
- The random sampling variability that is apparent in the four observed values [latex]x_1, \, x_2, \, x_3, \, x_4[/latex] is not apparent in the forecasted values [latex]\hat{X}_5, \, \hat{X}_6, \, \hat{X}_7[/latex]. Observed time series values typically exhibit random sampling variability; forecasted values tend to be smooth.
Our goal in this subsection is to discuss forecasting generally and to introduce techniques for determining point estimates and interval estimates for future values in a time series. The example that follows assumes that a valid ARMA model has been specified and the parameters in a time series model are known, rather than estimated from a realization of the time series. For a long realization (large n) or significant amounts of previous history associated with a particular time series, this assumption might not pose any problem. In order to derive a prediction interval for [latex]X_{n + h}[/latex], the white noise terms are assumed to be Gaussian white noise for mathematical tractability. The reason for this assumption will be apparent in the following example.
The previous example has illustrated the process for determining forecasted values and associated prediction intervals for an AR(1) time series model with known parameters. Consider generalizing this process for the h-step-ahead forecast. In order to obtain a point estimate for the forecast, take the conditional expected value of both sides of the model with [latex]X _ {n + h}[/latex] isolated on the left-hand side, which effectively results in: (a) present and past values of Xt are replaced by their observed values; (b) future values of Zt are replaced by their conditional expected values, which are zero; and (c) future values of Xt are replaced by their conditional expected values. After simplification, this results in the forecast value [latex]\hat{X} _ {n + h}[/latex].
As is typically the case in statistics, a point estimate is usually accompanied by an interval estimate which gives an indication of the precision of the point estimate. In a time series setting, a prediction interval for [latex]X_{n+h}[/latex] has the generic form
This formula assumes that the random future value at time [latex]n + h[/latex], denoted by [latex]X _ {n + h}[/latex], is normally distributed. This is usually achieved by assuming that the white noise terms consist of Gaussian white noise. Unlike confidence intervals, prediction intervals typically do not have widths that shrink to zero as the sample size n increases.
This ends the important topic of forecasting. Many more examples of forecasting will appear in subsequent sections in this chapter when special cases of ARMA([latex]p, \, q[/latex]) models are introduced. We now turn to another important statistical topic, which is model assessment.
8.2.3 Model Assessment
It is often the case that we have little or no information concerning the underlying physical mechanism governing a time series, so we must resort to an entirely data-driven approach to developing a time series model that adequately approximates the underlying probability mechanism. The usual approach to building a times series model consists of iterating through the following steps until a suitable model is formulated. The model building process is—by design—both iterative and interactive, making R an ideal platform for carrying out the process.
- Identify a tentative time series model.
- Estimate the unknown parameters of the tentative time series model.
- Assess the adequacy of the fitted time series model.
The third step is considered in this section. As an instance of this approach, let’s say we decide (based on inspecting plots of the time series, the sample autocorrelation function, and the sample partial autocorrelation function) that a shifted AR(2) time series model is a strong candidate for modeling a particular time series. After the parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] are estimated, we hope that the fitted model adequately models the underlying probability mechanism for the time series. If this is the case, then the signal associated with the time series has been captured, and all that should remain is noise. So how do we test whether or not the fitted model provides an adequate representation of the time series? One common approach taken in time series modeling is to assess whether the random shocks [latex]\left\{ Z_t \right\}[/latex] are mutually independent and identically distributed random variables with population mean zero and common population variance [latex]\sigma _ Z ^ {\, 2}[/latex]. But these Zt values are not observed by the modeler, so instead we inspect the residuals, which are estimates of the Zt values. In time series analysis, this important step is known as diagnostic checking or residual analysis. (This step is analogous to the similar step in regression analysis.) This process is the rough equivalent of goodness-of-fit testing from classical statistical theory. A residual value is defined as
The predicted value is the one-step-ahead forecast from the time [latex]t - 1[/latex]. Using the notation from the forecasting section, the residual at time t can be written as
This is one instance in which a more precise notation for a forecasted value would be helpful; this is more clearly written as
The hat is added to Zt in order to indicate that the parameters in the fitted model have been estimated from the observed time series. Only in a simulated time series with known parameters do we observe Zt. The residuals are ordered in time, so they can be viewed as a time series in their own right. If the hypothesized and fitted model are adequate, then the time series plot of the residuals will approximate a time series of white noise. The question here is how closely the residuals resemble white noise terms.
The behavior of the residuals is an indicator of whether the time series has been adequately modeled. If the model has been specified correctly and the parameter estimates are near their associated population values, then the residuals should appear to be white noise values, with common population mean zero and common population standard deviation. If this is not the case, then the search for an adequate time series model should continue.
A plot of the residuals over time is a crucial initial step in assessing whether they resemble white noise terms. Carefully examine the plot for any signs of trend, seasonality, or serial correlation. An example of a plot of Gaussian white noise was given in Figure 7.3. This step is just as important in residual analysis as was the inspection of the plot of the original time series. In addition, a plot of the sample autocorrelation function and the sample partial autocorrelation function of the residuals can be helpful in assessing whether the residuals closely approximate white noise. But rather than just a subjective visual inspection, we also want to confirm our intuition with a formal statistical test. The next four paragraphs briefly survey four statistical tests to assess the following null and alternative hypotheses:
- H0 : the residuals are mutually independent and identically distributed random variables
versus
- H1 : the residuals are not mutually independent and identically distributed random variables.
If there is no apparent visual trend, seasonality, or serial correlation in the residuals, then any one of the four hypothesis tests that follow can be conducted to confirm that the residuals do not exhibit any of these characteristics.
Count the number of significant spikes in the sample autocorrelation function. This test begins with a plot of the sample autocorrelation function of the residuals. If the residuals are well approximated by white noise terms, then the time series model can be judged to be adequate. The sample autocorrelation function values for white noise terms are approximately mutually independent and identically distributed [latex]N\left( 0, \, 1 / n \right)[/latex] random variables. So if the residuals closely approximate white noise, then any sample autocorrelation function value will fall between [latex]-1.96 / \sqrt{n}[/latex] and [latex]1.96 / \sqrt{n}[/latex] with approximate probability 0.95. We would like to conduct a hypothesis test in which the null hypothesis is that the sample autocorrelation function values of the residuals are independent [latex]N\left( 0, \, 1 / n \right)[/latex] random variables. A large number of sample autocorrelation values falling outside of the limits (which serves as the test statistic here) will result in rejecting the null hypothesis. So if each sample autocorrelation function value can be thought of as a toss of a biased coin in the case of the residuals being approximately white noise, then for, say, the first [latex]m = 40[/latex] such values, we expect [latex]40 \cdot 0.05 = 2[/latex] to fall outside of the limits [latex]\pm 1.96 / \sqrt{n}[/latex]. (Of course, the lag 0 sample autocorrelation [latex]r_0 = 1[/latex] is not included in the count.) In order to achieve an approximate level of significance [latex]\alpha = 0.05[/latex], if four or fewer of the 40 sample autocorrelation function values associated with the residuals fall outside of [latex]\pm 1.96 / \sqrt{n}[/latex], we fail to reject H0. The time series model is deemed to be adequate. But if five or more of the 40 sample autocorrelation function values associated with the residuals fall outside of [latex]\pm 1.96 / \sqrt{n}[/latex], this is evidence against the hypothesized model and we reject H0. The time series model is deemed to be inadequate. The p-value associated with four or fewer of the 40 sample autocorrelation function values associated with the residuals falling outside of the limits [latex]\pm 1.96 / \sqrt{40}[/latex] can be calculated with the R statement
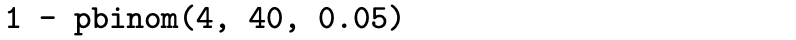
This statement returns

So the exact level of significance for this test is [latex]\alpha = 0.048[/latex], which is quite close to the desired level of significance of 0.05. Rather than using trial and error with the pbinom function to determine the number of lags to use as the critical value, the qbinom function can be used to determine the cutoff.
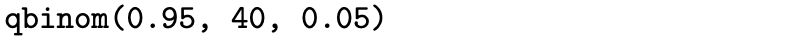
This statement returns

A similar analysis can be applied to lag counts other than the [latex]m = 40[/latex] sample autocorrelation function values illustrated above. This analysis assumes that the sample autocorrelation function values of the residuals are independent and identically distributed normal random variables. One weakness of this approach is that it simply counts the number of sample autocorrelation function values falling outside the 95% confidence interval limits and ignores (a) how far outside of the limits the values fall or (b) how close to the limits they fall when they lie within the limits. This weakness prompts us to seek a statistical test that captures all of the sample autocorrelation function values associated with the residuals and includes their magnitudes.
Box–Pierce test. Let rk be the lag k sample autocorrelation function value associated with the residuals of the fitted time series. As before, we only consider the first m such sample autocorrelation function values [latex]r_1, \, r_2, \, \ldots, \, r_m[/latex]. It is approximately true that for mutually independent and identically distributed residuals,
By the transformation technique, this implies that
Squaring this random variable gives
Assuming that the sample autocorrelation function values are uncorrelated, the sum of the first m of these random variables is
In the case in which r unknown model parameters have been estimated, the degrees of freedom are reduced by r:
This is the test statistic for the Box–Pierce test for serial correlation. Large values of this test statistic lead to rejecting H0 and indicate a poor fit. The null hypothesis is rejected at level of significance α when this test statistic is greater than [latex]\chi ^ 2 _ {m - r, \, \alpha }[/latex], where the first subscript is the number of degrees of freedom and the second subscript is the right-hand tail probability associated with this quantile of the chi-square distribution. There have been several approximations that occurred in formulating this statistical test. First, the rk values are only approximately normally distributed. Second, the rk values have variances which are less than [latex]1 / n[/latex] for small lag values k. To compound this approximation, these smaller initial variances are dependent on the model under consideration. Third, the rk values exhibit some serial correlation even when the residuals are mutually independent and identically distributed. These three weaknesses prompted a modification of the Box–Pierce test which provides a test statistic whose distribution more closely approximates the [latex]\chi ^ 2 (m - r)[/latex] distribution.
Ljung–Box test. The Box–Pierce test statistic was modified by Ljung and Box as
which is approximately [latex]\chi ^ 2 (m - r)[/latex], where r is the number of parameters estimated in the model. Comparing the Box–Pierce and Ljung–Box test statistics, since
for [latex]k = 1, \, 2, \, \ldots, \, m[/latex], the Ljung–Box test statistic always exceeds the Box–Pierce test statistic. The Box–Pierce test is more likely to accept a time series model with a poor fit than the Ljung–Box test for the same set of residuals. The Ljung–Box test should be used over the Box–Pierce because the probability distribution of its test statistic is closer to a [latex]\chi ^ 2 (m - r)[/latex] random variable under H0.
Turning point test. As opposed to focusing on the sample autocorrelation function associated with the residuals, the turning point test considers the number of turning points in the time series of residuals. A turning point in a time series is defined to be a value associated with a local minimum or a local maximum. A local minimum occurs when [latex]\hat{Z} _ {t - 1} > \hat{Z} _ t[/latex] and [latex]\hat{Z} _ {t} < \hat{Z} _ {t + 1}[/latex]. A local maximum occurs when [latex]\hat{Z} _ {t - 1} < \hat{Z} _ t[/latex] and [latex]\hat{Z} _ {t} > \hat{Z} _ {t + 1}[/latex]. The random number of turning points in a time series of length n comprised of strictly continuous observations is denoted by T. The strictly continuous assumption is in place to avoid ties in adjacent values. A turning point cannot occur at the first or last value of the time series. Keep in mind that there might be fewer residuals than original observations. The n that is used here is the number of residuals. As given in an exercise at the end of this chapter, if the residuals are mutually independent and identically distributed continuous random variables, then
Furthermore, even though T is a discrete random variable, it is well approximated by the normal distribution with population mean E[T] and population variance V[T] for a time series of mutually independent and identically distributed observations and large n. Thus, an appropriate test statistic for testing H0 is
which is approximately standard normal for large values of n. The null hypothesis is rejected in favor of the alternative hypothesis whenever the test statistic is less than [latex]- z_{\alpha / 2}[/latex] (which indicates fewer turning points than expected, which is an indicator of positive serial correlation among the residuals) or the test statistic is greater than [latex]z_{\alpha / 2}[/latex] (which indicates more turning points than expected, which is an indicator of negative serial correlation among the residuals).
This completes the brief introduction to four statistical tests concerning the mutual independence of the residuals. There are several other such tests, some of which are introduced in the exercises at the end of the chapter, but these four are representative of how such tests work. Three questions are given below concerning issues associated with the analysis of the residuals.
- What if two time series models are deemed adequate by these statistical tests?Instances frequently arise in which two or more candidate time series models fail to be rejected by the statistical tests on residuals that were just surveyed. In these cases, the modeler has four guiding principles. First, there might be physical considerations that might favor one model over another. An engineer, for example, might provide some engineering design insight concerning why one time series model would be favored over another. Second, the model with the best value of one of the model-selection statistics outlined in the next section, might be the appropriate choice. Third, if the modeler is torn between two time series models, selecting the model with the fewer parameters follows the parsimony principle. We would like a time series model that adequately captures the probabilistic aspects of the time series with the minimum number of parameters. Fourth, the purpose of the model, for example, description, explanation, prediction, or simulation, might drive the final choice of the model.
- If a time series model is deemed inadequate, can the analysis of the residuals guide the modeler toward a more suitable model?In some cases, the analysis of the residuals can indeed guide the modeler toward a more suitable time series model. Here is one instance. Let’s say that a shifted AR(1) model is being considered as a potential time series model:
Isolating the white noise term, this model can be written as
The parameters μ, [latex]\phi[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] are estimated from the observed time series, and the associated residuals are calculated and plotted. Rather than appearing as white noise, let’s say that the residuals appear to look like observations from an MA(1) time series model
where [latex]\left\{ W_t \right\}[/latex] is a time series of white noise. Combining the two previous equations, this would lead us in the direction of considering the model
which can be recognized as a shifted ARMA([latex]1, \, 1[/latex]) time series model. Thus, the ARMA([latex]1, \, 1[/latex]) composite model has been constructed from the two simpler models. We would then revisit parameter estimation procedures for the parameters μ, [latex]\phi[/latex], θ, and [latex]\sigma _ Z ^ {\, 2}[/latex], and perform model adequacy tests on the associated residual values on the fitted ARMA([latex]1, \, 1[/latex]) model.
- If a time series model is deemed adequate, should the noise terms be modeled as white noise or Gaussian white noise?The four statistical tests for autocorrelation do not assess the normality of the residuals. Drawing a histogram of the residuals is an important first step in terms of determining whether the residuals are normally distributed. If the histogram appears to be bell-shaped, then the Gaussian white noise aspect of the model is justified. Some time series analysts prefer to view a histogram of the standardized residuals, and the vast majority of these values should lie between [latex]-3[/latex] and 3. A QQ (quantile–quantile) plot is also useful for visually assessing normality, which can be graphed with the R function qqnorm. A QQ plot which is linear is an indication of normality. The behavior at the extremes of a QQ plot is typically more variable than at the center, so some analysts prefer to focus on the behavior between, say, the first and third quartiles. Assessing the normality of a histogram or the linearity of a QQ plot is subjective. Objective statistical tests for the normality of the residuals include the Shapiro–Wilk, Anderson–Darling, Cramer–von Mises, and Kolmogorov–Smirnov tests.
Analyzing the residuals is not the only way to assess the adequacy of a time series model. Another technique is known as overfitting. ARMA models with a single additional term are fitted to the original time series. This approach is analogous to forward selection in the stepwise approach to multiple regression. We will refer to the time series model under consideration as the tentative model and the overfitted models as enhanced models. For example, if an MA(1) model is being contemplated as a tentative time series model, then
- adding an additional moving average term yields the enhanced MA(2) model, and
- adding an autoregressive term yields the enhanced ARMA([latex]1, \, 1[/latex]) model.
The parameters for these two enhanced models should be fit to the original time series in the usual fashion. If both of the following two criteria are met, then the tentative time series model should be accepted as the final model.
- The parameter estimates in the enhanced models are close to the parameter estimates in the tentative model.
- The additional parameter in the enhanced models does not differ significantly from zero.
So in the example given above, the parameters in the tentative MA(1) model, θ1 and [latex]\sigma _ Z ^ {\, 2}[/latex], should be estimated from the original time series. Then the parameters in the enhanced MA(2) model, θ1, θ2, and [latex]\sigma _ Z ^ {\, 2}[/latex], should be estimated from the original time series. If a confidence interval for θ2 contains zero (or you fail to reject the null hypothesis [latex]H_0: \theta_2 = 0[/latex] versus the alternative hypothesis [latex]H_1: \theta_2 \ne 0[/latex]), and the other parameter estimates do not vary significantly between the two models, then the modeler concludes that the extra parameter in the MA(2) model is not necessary. The same type of thinking applies to the enhanced ARMA([latex]1, \, 1[/latex]) model. So in addition to a careful examination of the residuals, it is also helpful to overfit the model in the autoregressive and moving average directions to assess whether the additional term significantly improves the fit.
The model assessment techniques described in this subsection will be applied to actual time series later in this chapter.
8.2.4 Model Selection
Model-selection statistics are helpful when there are two or more tentative fitted ARMA([latex]p, \, q[/latex]) models for a time series which have been deemed adequate by the model assessment techniques outlined in the previous subsection. One naive approach to model selection is to just add additional terms to an ARMA([latex]p, \, q[/latex]) model and check the resulting sum of the squared residuals. This approach violates the parsimony principle because it is typically the case that adding parameters to a model results in a lower sum of squared residuals. Just blindly adding terms to minimize the sum of squares is likely to produce time series models with superfluous terms that contain no real explanatory value, which can potentially cause problems in the application of the model.
We seek some statistical measure that strikes a balance between simplicity and capturing the essence of the probabilistic mechanism governing the time series model. Some statistical measure which reflects the benefit of an additional parameter, but extracts a penalty for adding parameters would be helpful to strike this balance.
In the case in which the analyst is presented with multiple plausible tentative fitted models, a model-selection statistic such as Akaike’s Information Criterion might prove helpful in determining the best model. This statistic strikes a harmony between a simple model (which might not capture certain probabilistic aspects of the mechanism governing the time series) and a more complex model (which might contain unnecessary terms). This is the notion of a parsimonious model which uses as few parameters as possible to achieve adequate explanatory power. Akaike’s Information Criterion (AIC), named after Japanese statistician Hirotugu Akaike (1927–2009), extracts a penalty for each additional parameter that is added to the model. The AIC is
where r is the number of unknown parameters that are estimated and L is the likelihood function evaluated at the maximum likelihood estimators for the r unknown parameters. Since [latex]L( \cdot )[/latex] is maximized at the maximum likelihood estimators, the first part of the AIC statistic, namely [latex]-2 \ln \big( L( \cdot ) \big)[/latex], is minimized at the maximum likelihood estimator values because of the negative sign. The 2r term can be thought of as a penalty term for adding additional parameters to the model. Each additional parameter added to the model will probably decrease the first term in the AIC involving the log likelihood function, but will also increase the penalty term because r has been increased. The model with the lowest value of AIC is deemed by this model-selection statistic to be the most appropriate parsimonious time series model.
There are two variants of the AIC that provide improved ability to correctly identify a time series model.
- The AIC estimates the expected value of the Kullback–Leibler divergence of the estimated model from the true model, and there is a slight bias in the AIC which is significant for small values of n. The corrected Akaike Information Criterion, usually denoted by AICC, replaces the 2r penalty term with [latex]2rn / (n - r - 1)[/latex], resulting in
Since [latex]n / (n - r - 1) > 1[/latex], the AICC always exceeds the AIC for the same time series, meaning that the penalty for adding parameters is increased. The AICC will be more stingy than the AIC when it comes to adding parameters. The AICC model-selection statistic compensates for the AIC’s tendency to overfit models.
- Another variant to the AIC is the Bayesian Information Criterion (BIC) which replaces the penalty term 2r with [latex]r \ln \, n[/latex], resulting in
As shown in Figure 8.5 for a time series of length [latex]n = 50[/latex] and [latex]r = 0, \, 1, \, 2, \, \ldots , \, 5[/latex] unknown parameters, the BIC places an even higher penalty on additional terms in the time series model than the AIC and the AICC, which will result, on average, with time series models with fewer terms. Since the use of maximum likelihood estimation is required for calculating AIC, AICC, and BIC because all three are a function of the likelihood function L, the white noise terms are assumed to be normally distributed (that is, Gaussian white noise). A visual check of this assumption can be made by looking at a histogram of the residuals or a QQ plot of the residuals.
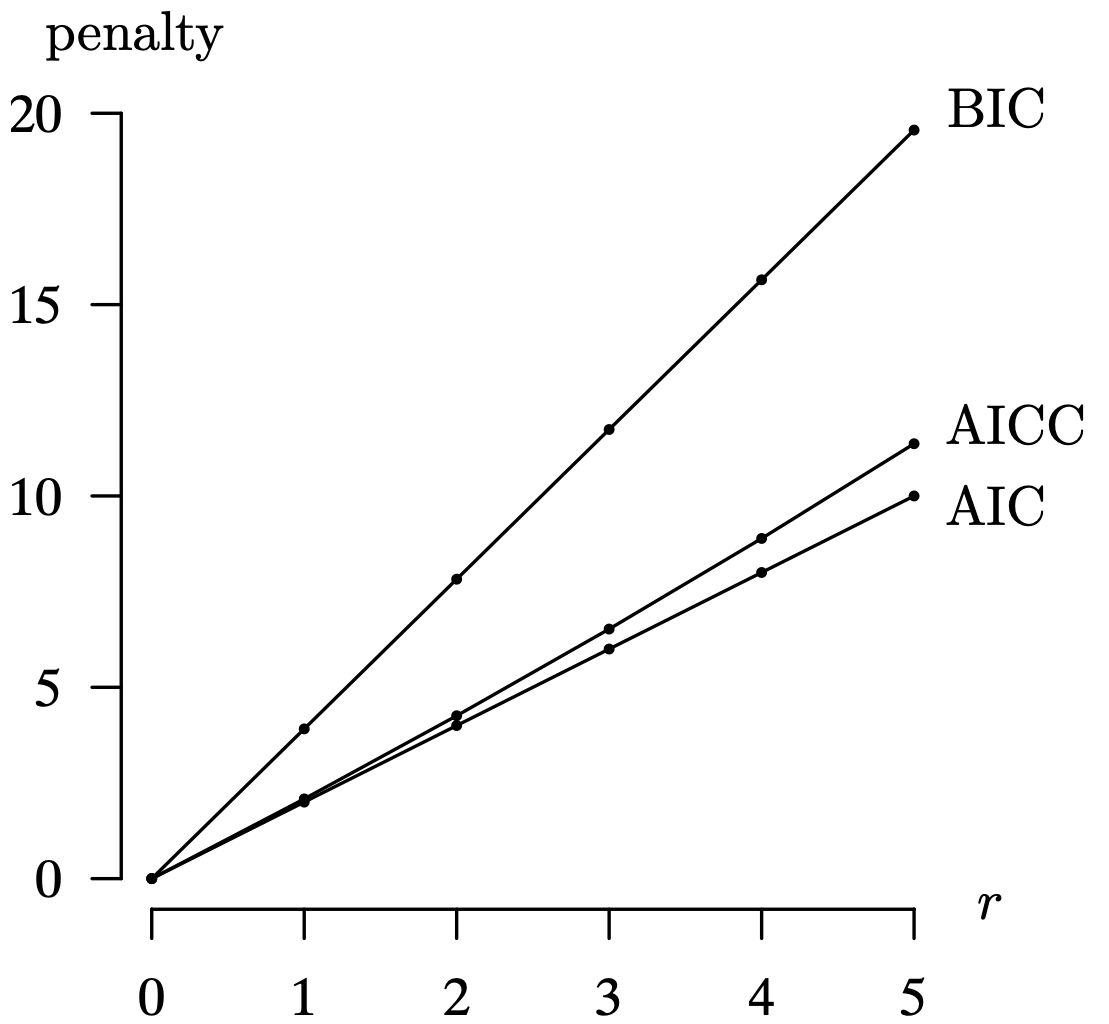
Long Description for Figure 8.5
The horizontal axis r ranges from 0 to 5 in increments of 1 unit. The vertical axis measuring penalty ranges from 0 to 20 in increments of 5 units. The statistic B I C has the largest penalty, and increases from (0, 0) to (5, 19). The statistic A I C C has the medium penalty and increases from (0, 0) to (5, 11). The statistic A I C has the lowest penalty and increases from (0, 0) to (5, 10). All data are estimated.
The time series analyst should consult with people who are familiar with the time series in order to glean whether there might be some aspects of the data set that might suggest one particular model or another. The analyst should also not necessarily assume that one of the models suggested in this chapter might be appropriate for every setting. There are seldom uniquely correct values for p and q but rather these model-selection statistics are helpful in comparing two fitted tentative models.
In principle, the general linear model and its associated statistical methods are all that is necessary to fit and assess an ARMA([latex]p, \, q[/latex]) model. Since each specific ARMA([latex]p, \, q[/latex]) model has its own idiosyncrasies, the first few special cases of the autoregressive and moving average models will be examined in the next chapter.
8.3 Exercises
-
8.1 Show that the general linear model
can be written in the form
-
8.2 For the ARMA time series model
- identify the time series model, and
- write the time series model in terms of the backshift operator B.
-
8.3 For the ARMA time series model
where [latex]\phi(B) = 1[/latex] and [latex]\theta(B) = 1 - 0.6B + 0.1B^2[/latex],
- identify the time series model, and
- write the time series model in purely algebraic form.
-
8.4 For the ARMA time series model
- identify the time series model, and
- write the time series model using the backshift operator.
-
8.5 Consider the special case of the general linear model
- Write this model in its causal representation.
- Write this model in its invertible representation.
-
8.6 Show that [latex]E \left[ X_t \right] = \mu[/latex] for the stationary shifted ARMA([latex]p, \, q[/latex]) model
-
8.7 Find [latex]E[X_t][/latex] for the shifted ARMA([latex]2, \, 1[/latex]) model
-
8.8 Let [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] be observations from an ARMA([latex]0, \, 0[/latex]) time series model with Gaussian white noise. The maximum likelihood estimator of the population variance of the Gaussian white noise derived in Example 8.10 is
An asymptotically exact confidence interval for [latex]\sigma _ Z ^ {\, 2}[/latex] derived in Example 8.11 is
Calculate and plot the actual coverage of a 95% confidence interval for [latex]\sigma _ Z ^ {\, 2}[/latex] as a function of n for [latex]n = 8, \, 9, \, \ldots , \, 256[/latex]. Use analytic methods rather than Monte Carlo simulation.
-
8.9 Let [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] be observations from an ARMA(0, \, 0) time series model with Gaussian white noise. Find the probability density function of the maximum likelihood estimator of the population variance of the Gaussian white noise
-
8.10 Let [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] be observations from an ARMA([latex]0, \, 0[/latex]) time series model with Gaussian white noise. As shown in Example 8.10, the maximum likelihood estimator of the population variance of the Gaussian white noise is
and a pivotal quantity for developing an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\sigma _ Z ^ 2[/latex] is
Find an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\sigma _ Z ^ 2[/latex].
-
8.11 Let [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] be observations from an ARMA([latex]0, \, 0[/latex]) time series model with Gaussian white noise having finite positive population variance [latex]\sigma _ Z ^ {\, 2}[/latex]. The maximum likelihood estimator of the population variance of the Gaussian white noise is
Conduct a Monte Carlo simulation experiment that provides convincing numerical evidence that
is an exact [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\sigma _ Z ^ {\, 2}[/latex] for one particular set of n, α, and [latex]\sigma _ Z ^ {\, 2}[/latex] of your choice.
-
8.12 Let X1 and X2 be jointly distributed random variables. The population mean and variance of X1 are [latex]\mu_{X_1}[/latex] and [latex]\sigma _ {X_1} ^ {\, 2}[/latex]. The population mean and variance of X2 are [latex]\mu_{X_2}[/latex] and [latex]\sigma _ {X_2} ^ {\, 2}[/latex]. The population correlation between X1 and X2 is [latex]\rho = \hbox{Corr} (X_1, \, X_2)[/latex]. The value of X2 is to be predicted as a linear function of X1 with [latex]mX_1 + b[/latex]. Find the values of m and b which minimize the mean square error of the prediction. In other words, find m and b which minimize
-
8.13 Consider an ARMA([latex]0, \, 0[/latex]) model with [latex]U(-1, \, 1)[/latex] white noise terms. Find an exact two-sided 95% prediction interval for [latex]X_{n + h}[/latex].
-
8.14 Suppose an ARMA(2, 1) time series model is a strong candidate for modeling a particular time series. A long time series is available for analysis, so n is large. The ARMA(2, 1) model is fitted and residuals are calculated. If the sample autocorrelation function associated with the residuals is calculated for the first 100 lags, how many values need to fall outside of [latex]\pm 1.96 / \sqrt{n}[/latex] in order to reject the null hypothesis H0, which corresponds to a good fit at a significance level that is less than [latex]\alpha = 0.05[/latex]?
-
8.15 Compare the expected p-values for the Box–Pierce and Ljung–Box tests for serial independence of a time series consisting of [latex]n = 100[/latex] mutually independent and identically distributed standard normal random variables. Consider only the first [latex]k = 40[/latex] lag values.
-
8.16 Let [latex]\hat{Z}_1, \, \hat{Z}_2, \, \ldots , \, \hat{Z}_n[/latex] be residual values associated with a fitted time series model. The Durbin–Watson test statistic defined by
is useful for testing the serial independence of the residuals.
- Conduct a Monte Carlo simulation experiment to estimate the expected value of D when [latex]\hat{Z}_1, \, \hat{Z}_2, \, \ldots , \, \hat{Z}_{1000}[/latex] are [latex]n = 1000[/latex] mutually independent and identically distributed standard normal random variables.
- Give an explanation for the result that you obtained in part (a).
-
8.17 The turning point test for serial dependence counts the number of turning points (the number of local minima and maxima) T in a time series of length n comprised of strictly continuous observations. A turning point cannot occur at the first or last value of the time series.
- Show that [latex]E[T] = 2 (n - 2) / 3[/latex] when the observations in the time series are mutually independent and identically distributed.
- Show that [latex]V[T] = (16n - 29) / 90[/latex] when the observations in the time series are mutually independent and identically distributed.
- Perform a Monte Carlo simulation that supports the values of E[T] and V[T] for a time series of length [latex]n = 101[/latex].
- Argue why T is approximately normally distributed with population mean E[T] and population variance V[T] for a time series of mutually independent and identically distributed observations and large n. Suggest an appropriate test statistic for testing the null hypothesis that there is no serial correlation in the time series.
-
8.18 Let [latex]X_1, \, X_2, \, X_3, \, X_4[/latex] be a time series of mutually independent and identically distributed continuous random variables. Let T be the number of turning points. Find the probability mass function of T.
-
8.19 The nonparametric difference–sign test for serial dependence counts the number of values in a time series of strictly continuous observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] in which [latex]X_i > X_{i - 1}[/latex], for [latex]i = 2, \, 3, \, \ldots, \, n[/latex]. Denote this count by T.
- Show that [latex]E[T] = (n - 1) / 2[/latex] when the observations in the time series are mutually independent and identically distributed.
- Show that [latex]V[T] = (n + 1) / 12[/latex] when the observations in the time series are mutually independent and identically distributed.
- Perform a Monte Carlo simulation that supports the values of E[T] and V[T] for a time series of length [latex]n = 101[/latex].
- Argue why T is approximately normally distributed with population mean E[T] and population variance V[T] for a time series of mutually independent and identically distributed observations and large n. Suggest an appropriate test statistic for testing the null hypothesis that there is no serial correlation in the time series.
-
8.20 Suppose an AR(1) model is being considered as a tentative time series model based on a realization of the time series. A single autoregressive parameter and a single moving average parameter is added to the tentative model, resulting in an ARMA([latex]2, \, 1[/latex]) enhanced model. Describe any problems that might arise by comparing the AR(1) time series model and the ARMA([latex]2, \, 1[/latex]) time series model.

