Chapter 9 Topics in Time Series Analysis
This chapter presents several topics in time series analysis. These include several of the popular time series models which are special cases of the ARMA(p, q), including the software required for fitting these models. The first section surveys the probability models and statistical methods associated with autoregressive models, more specifically the AR(1), AR(2), and AR(p) models. The second section surveys the probability models and statistical methods associated with autoregressive models, more specifically the MA(1), MA(2), and MA(q) models. It is important to know the properties of these special cases of the ARMA(p, q) model in order to successfully fit such a model to a realization of a time series. This will allow us to build an inventory of population autocorrelation and partial autocorrelation functions for these models that can be matched to their statistical counterparts for building a time series model. Time series analysts tend to use the smallest possible p and q values that adequately describe a time series. For this reason, separate subsections are devoted to the AR(1), AR(2), MA(1), and MA(2) time series models.
9.1 Autoregressive Models
Autoregressive models for a time series [latex]\left\{ X_t \right\}[/latex] will be considered in this section. An autoregressive model of order p is a special case of an ARMA(p, q) model with no moving average terms (that is, [latex]q = 0[/latex]), specified as
where [latex]\phi_1, \, \phi_2 , \, \ldots , \, \phi_p[/latex] are real-valued parameters and [latex]\left\{ Z_t \right\}[/latex] is a time series of white noise with population mean zero and population variance [latex]\sigma _ Z ^ {\, 2}[/latex]. The formulation of the AR(p) time series model looks quite similar to that of a multiple linear regression model with p independent variables. These independent variables are also known as predictors, regressors, or covariates in regression analysis. That is the genesis of the term autoregressive to describe this model. The prefix auto means self, indicating that this model has the current value of the time series [latex]\left\{ X_t \right\}[/latex] written as a linear function of the p previous versions of itself plus a white noise term Zt. The white noise term is critical to the model because without it, there would be no randomness in the model.
Rather than diving right into an AR(p) model, we first introduce the AR(1) and AR(2) models in separate sections because the mathematics are somewhat easier than the general case and some important geometry and intuition can be developed in these restricted models. In addition, an AR(1) or AR(2) model is often an adequate time series model in a particular setting. We always want a model with the fewest possible number of parameters that adequately approximates the underlying time series probability model. In the sections that follow, we will
- define the time series model for [latex]\left\{ X_t \right\}[/latex],
- determine the values of the parameters associated with a stationary model,
- derive the population autocorrelation and partial autocorrelation functions,
- develop algorithms for simulating observations from the time series,
- inspect simulated realizations to establish patterns,
- estimate the parameters from a time series realization [latex]\left\{ x_t \right\}[/latex],
- assess the adequacy of the time series model, and
- forecast future values of the time series using both point and interval estimates.
The purpose of deriving the population autocorrelation and partial autocorrelation functions is to build an inventory of shapes and patterns for these functions that can be used to identify tentative time series models from their sample counterparts by making a visual comparison between population and sample versions. This inventory of shapes and patterns plays an analogous role to knowing the shapes of various probability density functions (for example, the bell-shaped normal probability density function or the rectangular-shaped uniform distribution) in the analysis of univariate data in which the shape of the histogram is visually compared to the inventory of probability density function shapes.
In each section that follows, a single example of a time series will be carried through the various statistical procedures given in the list above. Stationarity plays a critical role in time series analysis because we are not able to forecast future values of the time series without knowing that the probability model is stable over time. This is why the visual assessment of a plot of the time series is always a critical first step in the analysis of a time series.
9.1.1 The AR(1) Model
The autoregressive model of order 1 is defined next. It has a closed-form expression for the population autocorrelation function and is frequently used in applications.
No subscript is necessary on the [latex]\phi[/latex] parameter because there is only one [latex]\phi[/latex] parameter in the AR(1) model. So there are two parameters that define an AR(1) model: the coefficient [latex]\phi[/latex] and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex].
The current value in the time series, Xt, is given by the parameter [latex]\phi[/latex] multiplied by the previous observed value in the time series, [latex]\phi X_{t - 1}[/latex], plus the current white noise term Zt. This model has the form of a simple linear regression model forced through the origin in which Xt is being predicted by the previous value of the time series [latex]X_{t-1}[/latex]. The parameter [latex]\phi[/latex] plays the role of the slope of the regression line. Thinking about an AR(1) model as a simple linear regression model suggests a statistical graphic that can be helpful in determining whether it is an appropriate model for a particular time series. A plot of xt on the vertical axis against [latex]x_{t - 1}[/latex] on the horizontal axis should be approximately linear if the AR(1) model is appropriate. The slope of the regression line on this plot corresponds to [latex]\phi[/latex], and the magnitude of the variability of the points about the regression line is determined by the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex].
Some authors prefer to parameterize the AR(1) model as
where [latex]\phi_0[/latex] and [latex]\phi_1[/latex] are real-valued parameters. We avoid this parameterization because the [latex]\phi_0[/latex] parameter is redundant in the sense that the population variance of the white noise [latex]\sigma _Z ^ {\, 2}[/latex] is absorbed into the [latex]\phi_0[/latex] parameter. Also, some authors use a – rather than a + between the terms on the right-hand side of the model.
To illustrate the thinking behind the AR(1) model in a specific context, let Xt represent the closing price of a particular stock on day t. The AR(1) model indicates that today’s closing price, denoted by Xt, equals [latex]\phi[/latex] multiplied by yesterday’s closing price ([latex]\phi X_{t - 1}[/latex]), plus today’s random white noise term Zt.
Stationarity
One initial important question concerning the AR(1) model is whether or not the model is stationary. Consider a thought experiment that determines whether an AR(1) model is stationary for specific values of [latex]\phi[/latex]. For one particular instance, consider [latex]\phi = 0[/latex]. In this case the AR(1) time series model reduces to
which is a time series model consisting solely of white noise. We know from Example 7.15 that a time series model of white noise terms is stationary. Now consider another instance, [latex]\phi = 1[/latex]. In this case the AR(1) time series model reduces to
which indicates that each value in the time series is the previous value plus the current white noise. In this case the population variance of the process is increasing with time because the number of white noise terms accumulate over time (see Example 7.8), so the AR(1) model with [latex]\phi = 1[/latex] violates one of the stationarity conditions given in Definition 7.6. The AR(1) model with [latex]\phi = 1[/latex] can be recognized as a random walk model from Example 7.4, and it was determined to be nonstationary in Example 7.17. So we have established that the AR(1) time series model is stationary for [latex]\phi = 0[/latex] and nonstationary for [latex]\phi = 1[/latex]. We now try to determine general restrictions on [latex]\phi[/latex] associated with a stationary AR(1) time series model. We take four different approaches to establishing the values of the coefficient [latex]\phi[/latex] that lead to a stationary model. The four approaches provide a review of several concepts defined previously.
Approach 1: Causality. In the derivations concerning the AR(1) time series model that follow, it will be beneficial to write the time series value Xt as a linear combination of the current and previous white noise values. This will allow us to use the definition of causality in Definition 8.2 to determine the values of [latex]\phi[/latex] associated with a stationary AR(1) model. To begin, recall that the AR(1) model given by
can be shifted in time and is equally valid for other t values, for example,
Using successive substitutions into the AR(1) model results in
This can be recognized as an MA(∞) time series model. Representing an AR(1) model as an MA(∞) model is known as duality. We now determine the constraints on the parameter [latex]\phi[/latex] which are required for stationarity. This is the form that is required for causality from Definition 8.2. The coefficients [latex]\psi_1, \, \psi_2, \, \ldots[/latex] for the AR(1) model from Definition 8.2 are
or in general, [latex]\psi_j = \phi ^ j[/latex], for [latex]j = 1, \, 2, \, \ldots[/latex]. Definition 8.2 requires that
for the time series model to be written in causal form. This summation is a geometric series that converges when [latex]|\phi| < 1[/latex], or equivalently, when [latex]-1 < \phi < 1[/latex], so these are the values of [latex]\phi[/latex] for which the AR(1) model is causal, which also implies that the model is stationary. Expressing the AR(1) model as an MA(∞) model will also be helpful in the subsequent derivation of the population autocovariance and autocorrelation functions.
Approach 2: Backshift operator. Although the purely algebraic derivation of the causal form of the AR(1) time series model using standard algebra techniques from Approach 1 works fine for establishing stationarity, there is an alternative approach which is slightly more elegant that exploits the backshift operator B. The AR(1) model
can be rewritten as
which can be expressed using the backshift operator as
The first-order polynomial [latex]\phi(B) = 1 - \phi B[/latex] generalizes to a polynomial in B of order p for an AR(p) model. Dividing both sides of this equation by [latex]1 - \phi B[/latex] gives
For values of [latex]\phi[/latex] satisfying [latex]-1 < \phi < 1[/latex], this can be recognized as a geometric series in B:
Executing the B operator converts this to the form
which is the same form that we encountered using the successive substitutions in the causality approach.
Approach 3: Unit roots analysis. Theorem 8.3 indicates that all AR(1) models are invertible and they are stationary when the root of
lies outside of the unit circle in the complex plane. The solution to this equation is
This root falls on the real axis in the complex plane and lies outside of the unit circle when
which is consistent with Approaches 1 and 2.
Approach 4: Definition of stationarity. We can also return to first principles to establish the values of [latex]\phi[/latex] associated with a stationary AR(1) model. This approach also results in the derivation of the population autocorrelation function. Recall from Definition 7.6 that a time series model is stationary if (a) the expected value of Xt is constant for all t, and (b) the population covariance between Xs and Xt depends only on the lag [latex]|t - s|[/latex]. Using the causal formula for the AR(1) time series model expressed as an MA(∞) time series model from Approach 1, the expected value of Xt is
for all values of the parameters [latex]\phi[/latex] and [latex]\sigma _ Z ^ {\, 2}[/latex], and all values of t. Again using the causal formula for the AR(1) time series model expressed as an MA(∞) time series model,
for [latex]-1 < \phi < 1[/latex]. Since [latex]E \left[ X_t \right] = 0[/latex] for all values of t and the population autocovariance function depends only on the lag [latex]|t - s|[/latex], we conclude that the AR(1) process is stationary when [latex]-1 < \phi < 1[/latex]. So the population autocovariance function can be expressed in terms of the lag k as
Dividing by the population autocovariance function by
gives the population autocorrelation function
Based on the four approaches, we now know beyond a shadow of doubt that an AR(1) model is stationary for values of the parameter [latex]\phi[/latex] satisfying [latex]-1 < \phi < 1[/latex]. This derivation constitutes a proof of the following result, which will be stated for just the nonnegative lags. Many authors list the lags as [latex]k = \pm 1, \, \pm 2, \, \ldots \,[/latex], but we appeal to Theorem 7.1 to cover the negative lags and only report the nonnegative lags in all of the population autocorrelation functions given in this chapter.
The derivation of [latex]\rho(k) = \phi ^ k[/latex] for [latex]k = 0, \, 1, \, 2, \, \ldots[/latex] provides still further evidence of the restriction that [latex]-1 < \phi < 1[/latex]. If [latex]\phi[/latex] were equal to a value outside of this range, say [latex]\phi = 2[/latex], this would result in population correlation values outside of the range [latex]-1 \le \rho(k) \le 1[/latex].
For all admissible values of [latex]\phi[/latex] on the interval [latex]-1 < \phi < 1[/latex], we see from the formula [latex]\rho(k) = \phi ^ k[/latex] for [latex]k = 0, \, 1, \, 2, \, \ldots[/latex] that there will be a geometric decline in the magnitude of the values in the population autocorrelation function as the lag k increases. There are two distinct cases for [latex]\phi[/latex], however, which will result in population autocorrelation functions with distinctly different shapes. The first case is [latex]0 < \phi < 1[/latex], which gives positive population autocorrelation values at all lags. This is associated with a time series that lingers on one side of the mean. How long it lingers depends on the magnitude of [latex]\phi[/latex]. Larger values of [latex]\phi[/latex] indicate that nearby observations will tend to be more likely to be on the same side of the mean, and therefore the time series will tend to linger longer on one side of the mean. The second case is [latex]-1 < \phi < 0[/latex], which gives population autocorrelation function values which alternate in sign and is associated with a time series that is likely to jump from one side of the mean to the other for adjacent observations. These two cases are illustrated in Figure 9.1 for the first 8 lags of the population autocorrelation function for [latex]\phi = 0.8[/latex] and [latex]\phi = -0.8[/latex].

Long Description for Figure 9.1
In both graphs, the horizontal axis k ranges from 0 to 8 in increments of 1 unit. The vertical axis rho of k ranges from negative 1 to 1 in increments of 1 unit. In the first graph for phi equals 0.8, a horizontal line is drawn at 0. The values of rho of k decrease progressively from 1 to 0.2 for k values 0 to 8. The second graph for phi equals negative 0.8 exhibits a damped sinusoidal fashion. The values of rho for even k values are positive, decreasing from 1 to 0.2. The values of rho for odd k values are negative, increasing from negative 0.8 to negative 0.2. All data are estimated.
Population Partial Autocorrelation Function
We now determine the population partial autocorrelation function for an AR(1) model. By Definition 7.4, the population lag 0 partial autocorrelation value is [latex]\rho ^ * (0) = 1[/latex]. The population lag 1 partial autocorrelation value is [latex]\rho ^ * (1) = \rho (1) = \phi[/latex]. The population lag 2 partial autocorrelation is
This is consistent with the result from Example 7.22 from first principles. Notice that the second column of the matrix in the numerator is a multiple of the first column of the matrix in the numerator. This is why the determinant of the numerator is zero. The population lag 3 partial autocorrelation is
Again, the determinant in the numerator is zero because the third column is a multiple of the first column. This pattern continues for the lag k population partial autocorrelation function, which has a first column of the numerator matrix [latex]\left[ 1, \, \phi , \, \phi ^ 2 , \, \ldots , \, \phi ^ {k - 1} \right] ^ \prime[/latex] and last column [latex]\left[ \phi, \, \phi ^ 2 , \, \phi ^ 3 , \, \ldots , \, \phi ^ k \right] ^ \prime[/latex]. Since the last column of the numerator matrix is a multiple of the first column of the numerator matrix, the determinant of the numerator matrix is zero. This constitutes a proof of the following result.
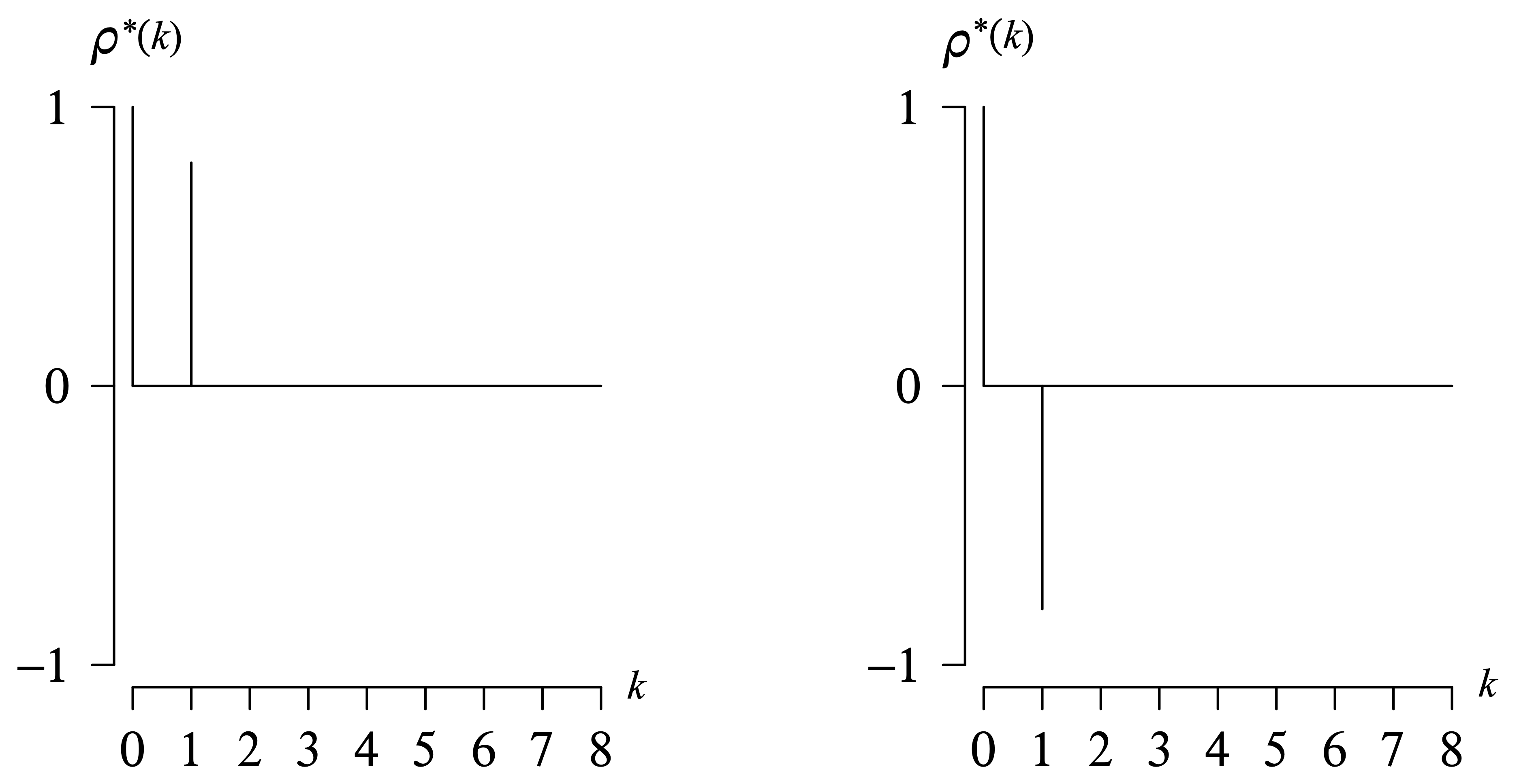
Figure 9.2 shows the first 8 lags of the population partial autocorrelation function for [latex]\phi = 0.8[/latex] and [latex]\phi = -0.8[/latex]. These are the same parameter settings as in Figure 9.1. Unlike the population autocorrelation function which tails off in magnitude for increasing lags, the population partial autocorrelation cuts off after lag 1. When plotting the corresponding sample analogs, it is typically easier to visually assess a function cutting off rather than tailing off, particularly if there is significant random sampling variability in the observed time series.
Long Description for Figure 9.2
In both graphs, the horizontal axis k ranges from 0 to 8 in increments of 1 unit. The vertical axis rho star of k ranges from negative 1 to 1 in increments of 1 unit. In the first graph for phi equals 0.8, a horizontal line is drawn at 0. The values of the rho star of k for k values 0 and 1 are 1 and 0.8, respectively. The second graph for phi equals negative 0.8 has rho star of k values 1 and negative 0.8 for k values 0 and 1, respectively. All data are estimated.
The Shifted AR(1) Model
The population mean function for the AR(1) model is [latex]E \left[ X_t \right] = 0[/latex]. This model is not of much use in practice because most real-world time series are not centered around zero. Adding a third parameter μ overcomes this shortcoming. Since population variance and covariance are unaffected by a shift, the associated population autocorrelation and partial autocorrelation functions remain the same as those given in Theorems 9.1 and 9.2. Likewise, the condition for stationarity is unchanged.
Simulation
An AR(1) time series can be simulated by appealing to the defining formula for the AR(1) model. Iteratively applying the defining formula for an AR(1) model
results in the simulated values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. The difficult aspect of this algorithm is how to generate the first value X1 because there is no X0 available. For simplicity, assume that the white noise terms are Gaussian white noise. Since the expected value of Xt is [latex]E \left[ X_t \right] = 0[/latex], the population variance of Xt is
and linear combinations of mutually independent normally distributed random variables are normal, then the first simulated observation
The algorithm given as pseudocode below generates an initial time series observation X1 as indicated above, and then uses an additional [latex]n - 1[/latex] Gaussian white noise terms [latex]Z_2, \, Z_3, \, \ldots, \, Z_n[/latex] to generate the remaining time series values [latex]X_2, \, X_3, \, \ldots, \, X_n[/latex] using the AR(1) defining formula from Definition 9.1. Indentation denotes nesting in the algorithm.
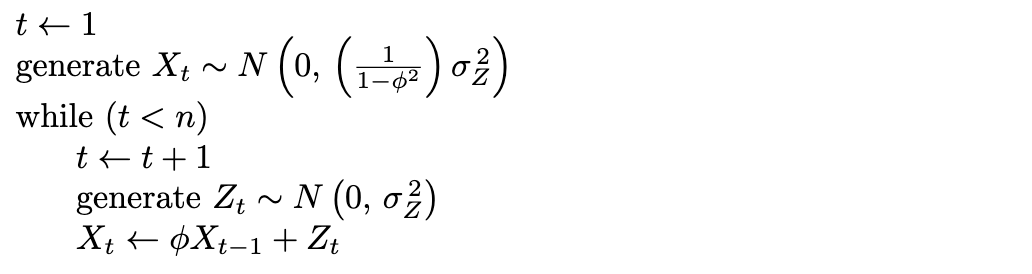
The three-parameter shifted AR(1) time series model which includes a population mean parameter μ can be simulated by simply adding μ to each time series observation generated by this algorithm. The next example implements this algorithm in R.
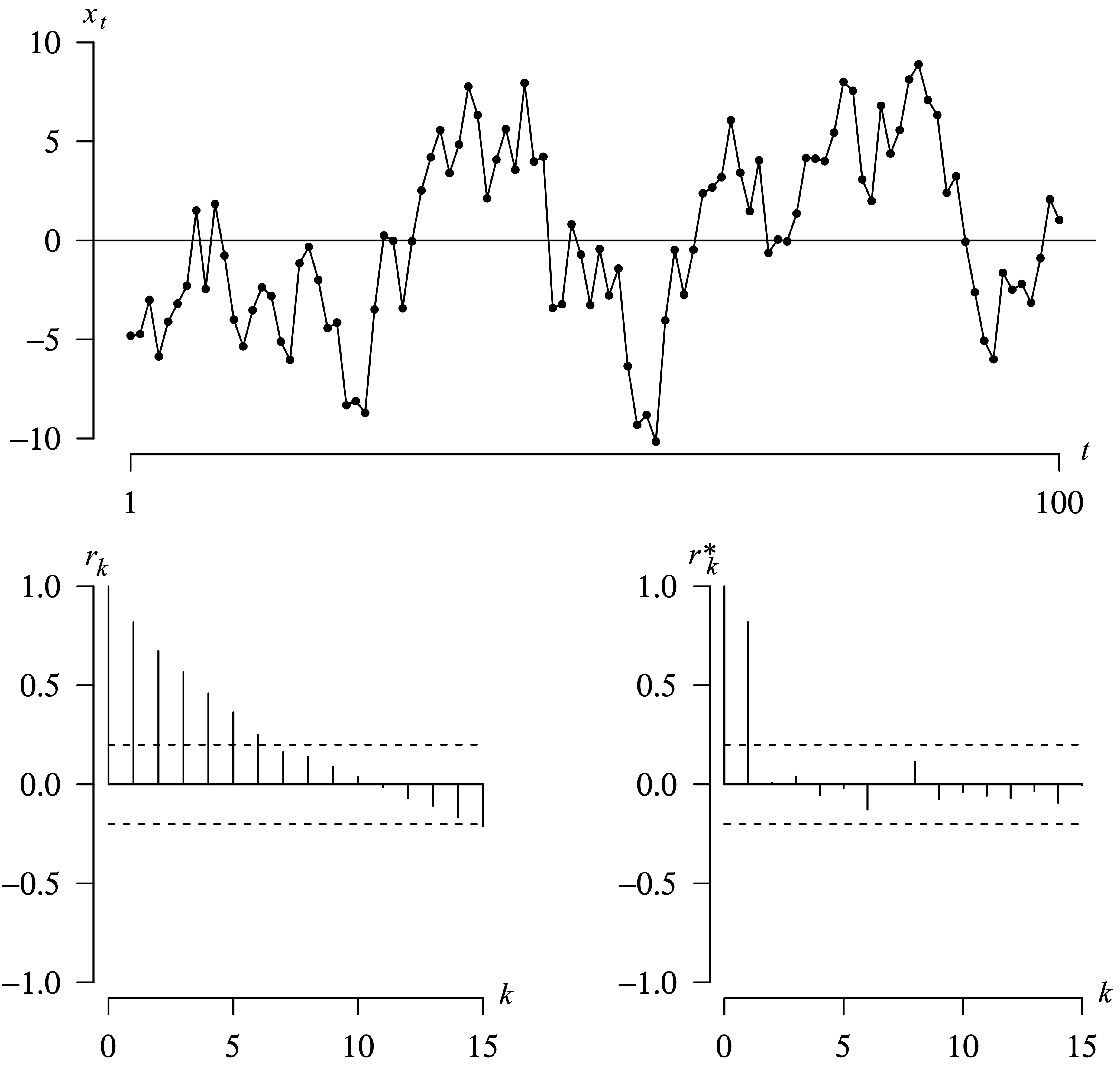
Long Description for Figure 9.3
In the time series plot, the horizontal axis t ranges from 1 to 100. The vertical axis x subscript t ranges from negative 10 to 10 in increments of 5 units. The graph behaves in a spike pattern. A horizontal line is drawn at x subscript t equals 0. The graph increases from negative 5 to 2 as t increases from 0 to 10. It then progressively decreases to negative 6 at t equals 13, then increases to 0 at t equals 20, and again decreases to negative 8 at t equals 26. It then increases to 8 and decreases to a minimum of negative 11 at t equals 55, again increases to 9 at t equals 85, and decreases to negative 7 at t equals 93. In the correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The dashed horizontal lines are drawn at negative 0.2 and 0.2. The values of r subscript k decrease from 1.0 to 0.1 for k values 0 through 10. The values then decrease from negative 0.01 to negative 0.2 as k increases from 11 to 15. For the partial autocorrelation function, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r star subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The values of r star subscript k value for k values 0, 1, 3, and 8 are 1.0, 0.7, 0.01, and 0.15, respectively. For the remaining k values, the r star subscript k values are negative, ranging between negative 0.2 and 0.0. All data are estimated.
We recommend running the simulation code from the previous example several dozen times in a loop and viewing the associated plots of xt, rk, and [latex]r_k^*[/latex] in search of patterns. A call to the R function Sys.sleep between the displays of the trio of plots can be used to include an artificial time delay to allow you to inspect the plots. This will allow you to see how various realizations of a simulated AR(1) time series model vary from one realization to the next. So when you then view a single realization of a real-life time series, you will have a better sense of how far these plots might deviate from their expected patterns.
There is a second way to simulate observations from an AR(1) time series. This second technique starts the time series at an initial arbitrary value, and then allows the time series to “warm up” or “burn in” for several time periods before producing the first observation X1. A reasonable initial arbitrary value for the standard AR(1) model is 0; a reasonable initial arbitrary value for the shifted AR(1) model is μ. This is the approach taken by the built-in R function named arima.sim (for autoregressive moving average simulation), which simulates a realization of a time series. Using the arima.sim function saves a few keystrokes over the approach taken in the previous example, as illustrated next.
The remaining topics associated with the AR(1) time series model are statistical in nature: parameter estimation, model assessment, model selection, and forecasting. A sample time series that will be revisited throughout these topics will be introduced next.
Parameter Estimation
There are two parameters, [latex]\phi[/latex] and [latex]\sigma _ Z ^ {\, 2}[/latex], to estimate in the standard AR(1) model
There are three parameters, μ, [latex]\phi[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex], to estimate in the shifted AR(1) model
The three parameter estimation techniques outlined in Section 8.2.1 are applied to the shifted AR(1) time series model next.
Approach 1: Method of moments. In the case of the shifted AR(1) model, we match the population and sample (a) first-order moments, (b) second-order moments, and (c) lag 1 autocorrelation. Placing the population moments on the left-hand side of the equation and the associated sample moments on the right-hand side of the equation results in three equations in three unknowns:
or
These equations can be solved in closed form for the three unknown parameters μ, [latex]\phi[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] yielding the method of moments estimators
This constitutes a proof of the following result.
These point estimators are random variables and have been written as a function of the random time series values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. For observed time series values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], the lowercase versions of the formulas will be used.
Approach 2: Least squares. Consider the shifted stationary AR(1) model
For least squares estimation, we first establish the sum of squares S as a function of the parameters μ and [latex]\phi[/latex] and use calculus to find the least squares estimators of μ and [latex]\phi[/latex]. This will result in a slight difference between the usual pattern of using the sample mean [latex]\bar x[/latex] to estimate the population mean μ. Once these least squares estimators have been determined, the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex] will be estimated.
The sum of squared errors is
The partial derivatives of S with respect to μ and [latex]\phi[/latex] are
and
Equating the first of the partial derivatives to zero yields
or
or
or
where
Equating the second of the partial derivatives to zero yields
or
So the ordinary least squares estimators for μ and [latex]\phi[/latex] can be determined by numerically solving the simultaneous equations
for [latex]\hat \mu[/latex] and [latex]\hat \phi[/latex].
The last parameter to estimate is [latex]\sigma _ Z ^ {\, 2}[/latex]. Since
for an AR(1) time series model, the population variance of the white noise can be expressed as
Replacing [latex]\phi[/latex] by the estimator r1 because [latex]\rho(1) = \phi[/latex], and replacing [latex]\gamma(0) = V \left[ X_t \right][/latex] by the estimator [latex]c_0 = \frac{1}{n} \sum_{t\,=\,1}^n \left( X_t - \bar X \right) ^ 2[/latex] gives the point estimator
which matches the method of moments estimator from Theorem 9.4. This derivation constitutes a proof of the following result.
We now apply these techniques to the beaver temperature data set from Example 9.3.
Since
contain the[latex]n - 2[/latex] common values [latex]X_2, \, X_3, \, \ldots, \, X_{n - 1}[/latex], one approximation that can be applied to the least squares estimates is to assume that [latex]\bar X _ 1 \cong \bar X _ 2 \cong \bar X[/latex] for large values of n, which allows for closed-form approximate least squares estimators:
As a secondary additional approximation, the denominator of [latex]\hat \phi[/latex] with the first approximation in place,
is approximately equal to
for large values of n. With this additional assumption, the least squares estimate for [latex]\phi[/latex] reduces to the approximate least squares estimate
which is the method of moments estimator of [latex]\phi[/latex] because [latex]\rho(1) = \phi[/latex] for an AR(1) model. With both approximations in place, the least squares estimators exactly match the method of moments estimators. This is why the estimates from the two techniques are so close.
Approach 3: Maximum likelihood estimation. The likelihood function is the joint probability density function of the observed values in the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] in a shifted AR(1) model is
where the [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] arguments on L and the μ, [latex]\phi[/latex], and [latex]\sigma _Z ^ {\, 2}[/latex] arguments on f have been dropped for brevity. It is not possible to simply multiply the marginal probability density functions because the values in the AR(1) time series model are correlated. In order to use maximum likelihood estimation, we make the additional assumption that the white noise terms [latex]Z_1, \, Z_2, \, \ldots, \, Z_n[/latex] are in fact Gaussian white noise terms:
for [latex]t = 1, \, 2, \, \ldots, \, n[/latex], which is the probability density function of a [latex]N\left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex] random variable. Ignoring Z1 temporarily, the joint probability density function of the mutually independent white noise random variables [latex]Z_2, \, Z_3, \, \ldots, \, Z_n[/latex] is
for [latex]\left( z_2, \, z_3, \, \ldots , \, z_n \right) \in {\cal R} ^ {n - 1}[/latex]. The shifted AR(1) model
applies for all values of t, so
Solving these equations for [latex]X_2, \, X_3, \, \ldots, \, X_n[/latex], consider the transformation of the [latex]Z_2, \, Z_3, \, \ldots , \, Z_n[/latex] values
conditioned on [latex]X_1 = x_1[/latex], which is a one-to-one transformation from [latex]{\cal R}^{n - 1}[/latex] to [latex]{\cal R}^{n - 1}[/latex] with inverse transformation
and Jacobian
By the transformation technique, the joint probability density function of [latex]X_2, \, X_3, \, \ldots, \, X_n[/latex] conditioned on [latex]X_1 = x_1[/latex] is
for [latex]\left( x_2, \, x_3, \, \ldots , \, x_n \right) \in {\cal R} ^ {n - 1}[/latex] and [latex]x_1 \in {\cal R}[/latex]. The final step in the derivation of the likelihood function involves determining the marginal distribution of X1. Since
the probability density function of X1 is
The joint probability density function of [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] is the product of the conditional probability density function and the marginal probability density function:
for [latex]\left( x_1, \, x_2, \, \ldots, \, x_n \right) \in {\cal R} ^ n[/latex]. So the likelihood function is
where the unconditional sum of squares is
The associated log likelihood function is
The maximum likelihood estimators [latex]\hat \mu[/latex], [latex]\hat \phi[/latex], and [latex]\hat \sigma _ Z ^ {\, 2}[/latex] satisfy
Although the third equation satisfies
numerical methods are required to solve the equations.
Maximum likelihood estimation will be illustrated in the next example.
Table 9.2 summarizes the point estimators that have been calculated in the previous three examples for the [latex]n = 62[/latex] beaver temperatures. The point estimators associated with the three methods are quite close for this particular time series.
|
Method |
[latex]\hat \mu[/latex] |
[latex]\hat \phi[/latex] |
[latex]\hat \sigma _Z ^ {\, 2}[/latex] |
|---|---|---|---|
|
Method of moments |
37.90 |
0.7894 |
0.01734 |
|
Ordinary least squares |
37.91 |
0.7972 |
0.01762 |
|
Maximum likelihood estimation |
37.91 |
0.7850 |
0.01697 |
The R function ar fits autoregressive models. The parameter estimates from the three previous examples could have been calculated with the following four R statements.

Table 9.3 contains the point estimates returned by the ar function. The tiny differences between some of the entries in Tables 9.2 and 9.3 might be due to slightly different approximations and/or roundoff in the optimization routines.
|
Method |
[latex]\hat \mu[/latex] |
[latex]\hat \phi[/latex] |
[latex]\hat \sigma _Z ^ {\, 2}[/latex] |
|---|---|---|---|
|
Method of moments (Yule–Walker) |
37.90 |
0.7894 |
0.01792 |
|
Ordinary least squares |
37.90 |
0.7972 |
0.01724 |
|
Maximum likelihood estimation |
37.90 |
0.7865 |
0.01699 |
We have now derived and illustrated the three point estimation techniques, the method of moments, least squares, and maximum likelihood estimation, for the parameters in an AR(1) model from a realization of a time series consisting of n observations. Which of these techniques provides the best point estimators? This is not an easy question to answer because there are a large number of factors, such as the sample size n, the values of the parameters in the model, and the fact that there are three parameters to estimate. There will not necessarily be one universal answer to the question. We do a focused evaluation on the point estimator for [latex]\phi[/latex] because it typically differs for the three methods of point estimation. The mean square error associated with the point estimate for [latex]\phi[/latex] is
The following R code conducts a Monte Carlo simulation experiment which estimates the mean square error of the three point estimators for [latex]\phi[/latex] for 40,000 replications. We selected the time series model with [latex]\mu = 38[/latex], [latex]\phi = 0.8[/latex], [latex]\sigma _ Z = 0.13[/latex], and [latex]n = 62[/latex], which are parameters that are near the estimated parameters in the last three examples involving the time series of beaver temperatures.

After a call to set.seed(4) to establish the random number stream, three runs of this simulation yielded the following estimated mean squared error values:
Furthermore, confidence intervals for the three methods do not overlap. Since small values of the mean square error are preferred, we conclude that the maximum likelihood estimator is the preferred estimator for these parameter settings, followed by the least squares estimator, followed by the method of moments estimator in a distant third place.
The focus on estimation thus far has been on point estimation techniques. We also want to report some indication of the precision associated with these point estimators. In the previous example, the sampling distributions of [latex]\hat \mu[/latex], [latex]\hat \phi[/latex], and [latex]\hat \sigma _ Z ^ {\, 2}[/latex] in the AR(1) model are too complicated to derive analytically. As an illustration of a confidence interval for one of the parameters, we use the asymptotic normality of the maximum likelihood estimator of [latex]\phi[/latex] in the result:
This result leads to an asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\phi[/latex].
This asymptotically exact confidence interval will now be illustrated with the time series of active beaver temperatures from the three previous examples.
Model Assessment
Now that techniques for point and interval estimates for the parameters in the AR(1) model have been established, we are interested in assessing the adequacy of the AR(1) time series model. This will involve an analysis of the residuals. Recall from Section 8.2.3 that the residuals are defined by
or
Since [latex]\hat{X} _ {t}[/latex] is the one-step-ahead forecast from the time origin [latex]t - 1[/latex], this is more clearly written as
Therefore, for the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] and the fitted AR(1) model with parameter estimates [latex]\hat \mu[/latex] and [latex]\hat \phi[/latex], the residual at time t is
for [latex]t = 2, \, 3, \, \ldots, \, n[/latex] via Example 8.12. The next example shows the steps associated with assessing the adequacy of the AR(1) model for the active beaver temperature time series.
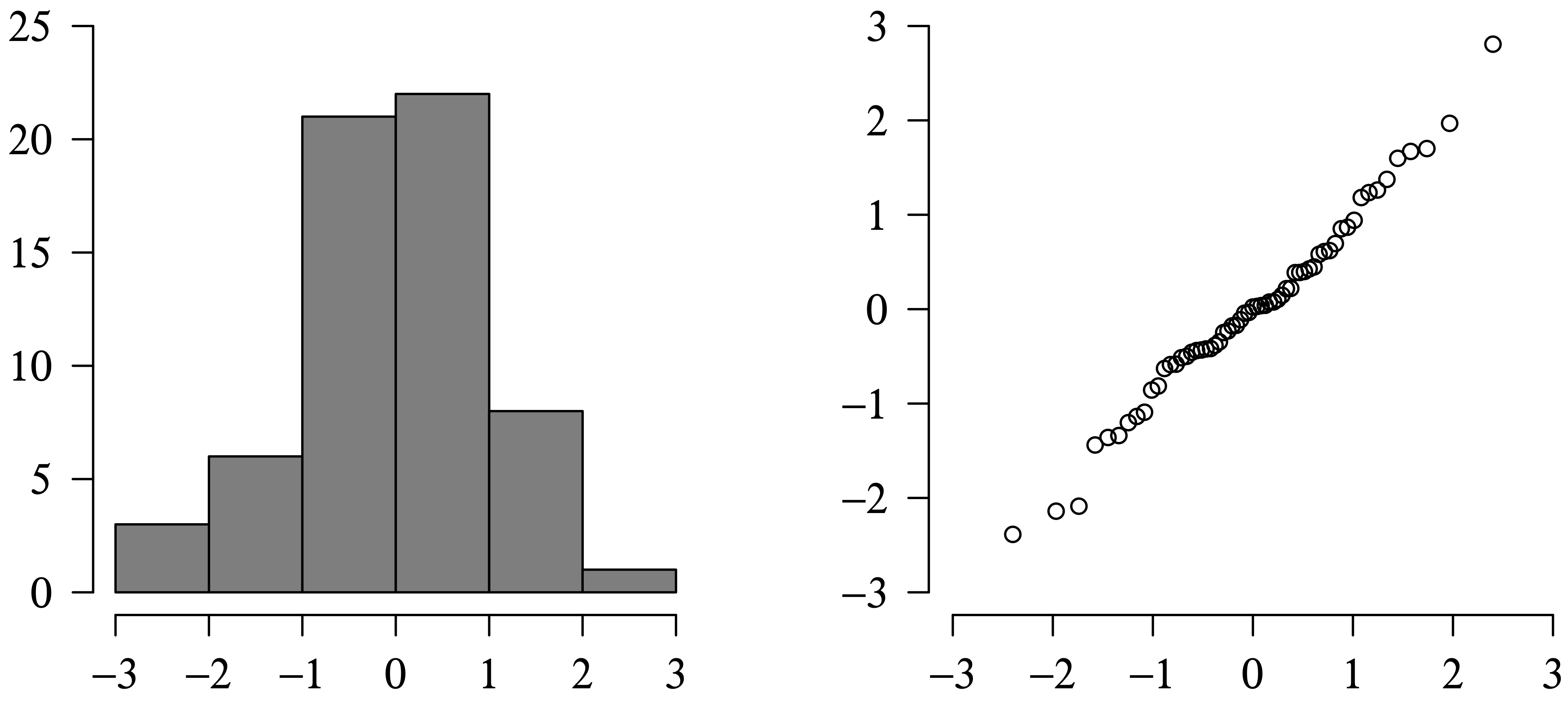
Long Description for Figure 9.10
In a histogram, the horizontal axis ranges from negative 3 to 3 in increments of 1 unit. The vertical axis ranges from 0 to 25 in increments of 5 units. From negative 3 to 3, there are six bars that are distributed normally. The frequency of the bars from negative 3 to 3 is 3, 6, 21, 22, 8, and 1, respectively. In the Q Q plot, the horizontal and the vertical axes range from negative 3 to 3 in increments of 1 unit. Sixty one data points are plotted in a roughly linear trend. A cluster of 55 data points is formed between negative 2 and 2 on the horizontal axis and between negative 1.5 to 1.5 on the vertical axis. All data are estimated.
We have seen a number of indicators that the AR(1) time series model is an adequate model for the active beaver temperatures. But how do we know that there is not a better model with more terms lurking below the surface that might provide a better fit? The next subsection considers the process of model selection.
Model Selection
One way of eliminating the possibility of a better time series model is to overfit the tentative AR(1) time series model with ARMA(p, q) models of higher order. We have not yet surveyed the techniques for estimating the parameters in these models with additional terms, so for now we will let the arima function in R estimate their parameters and compare them via their AIC (Akaike’s Information Criterion) statistics. The AIC statistic was introduced in Section 8.2.4.
In some applications, just describing the time series model for the beaver temperatures in the active state with the fitted AR(1) model is adequate. In other applications, simulating the values in the fitted AR(1) model is the goal. But in many application areas, particularly economics, there is often an interest in forecasting future values of a time series from a realization. In our setting, we might be interested in this particular beaver’s future temperature based on the [latex]n = 62[/latex] temperature values collected. The next subsection considers forecasting for the AR(1) model.
Forecasting
We now pivot to the development of a procedure to forecast future values of a time series that is governed by an AR(1) model. To review the notation for forecasting, the observed time series values are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. The forecast is being made at time [latex]t = n[/latex]. The random future value of the time series that is h time units in the future is denoted by [latex]X_{n + h}[/latex]. The associated forecasted value is denoted by [latex]\hat{X}_{n + h}[/latex], and is the conditional expected value
We would like to calculate this forecasted value and an associated prediction interval for the AR(1) model. As in Section 8.2.2, we assume that all parameters are known in the derivations that follow.
Recall from Example 8.12 that the forecasted value for one time unit into the future for a shifted AR(1) model is
We would like to generalize this so as to find the forecasted value h time units into the future. In other words, we want to find [latex]\hat{X} _ {n + h}[/latex]. The shifted AR(1) model is
Replacing t by [latex]n + h[/latex], which is the time value of interest, gives
Taking the conditional expected value of each side of this equation results in
Iterating on this equation for time values that are sequentially one time unit closer to the present time [latex]t = n[/latex] yields
Notice that the forecasted value is a function of xn, but not a function of [latex]x_1, \, x_2, \, \ldots, \, x_{n - 1}[/latex]. This is a sensible forecast in the sense that for a long time horizon h into the future and a stationary shifted AR(1) model with [latex]-1 < \phi < 1[/latex],
If you were asked to forecast your temperature one year from now, you would probably say 98.6° Fahrenheit (or whatever your average temperature might be), regardless of whether you are healthy or have a fever right now. Long-term forecasts for stationary time series models always tend to the population mean.
As is typically the case in statistics, we would like to pair our point estimator [latex]\hat{X}_{n + h}[/latex] with an interval estimator, which is a prediction interval in this setting. The prediction interval gives us an indication of the precision of the forecast. In order to derive an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]X _ {n + h}[/latex], it is helpful to write the shifted AR(1) model as a shifted MA(∞) model. Using successive substitutions, each one time unit prior to the previous substitution,
For [latex]-1 < \phi < 1[/latex] corresponding to a stationary shifted AR(1) model, the limiting expression for Xt is
which is a shifted MA(∞) model. Replacing t with [latex]n + h[/latex] results in
Taking the conditional variance of both sides of this equation yields
because the error terms at time n and prior are observed and can therefore be treated as constants. Assuming Gaussian white noise terms, an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]X _ {n + h}[/latex] is
In most practical problems, the parameters in this prediction interval will be estimated from data, which results in the following approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval.
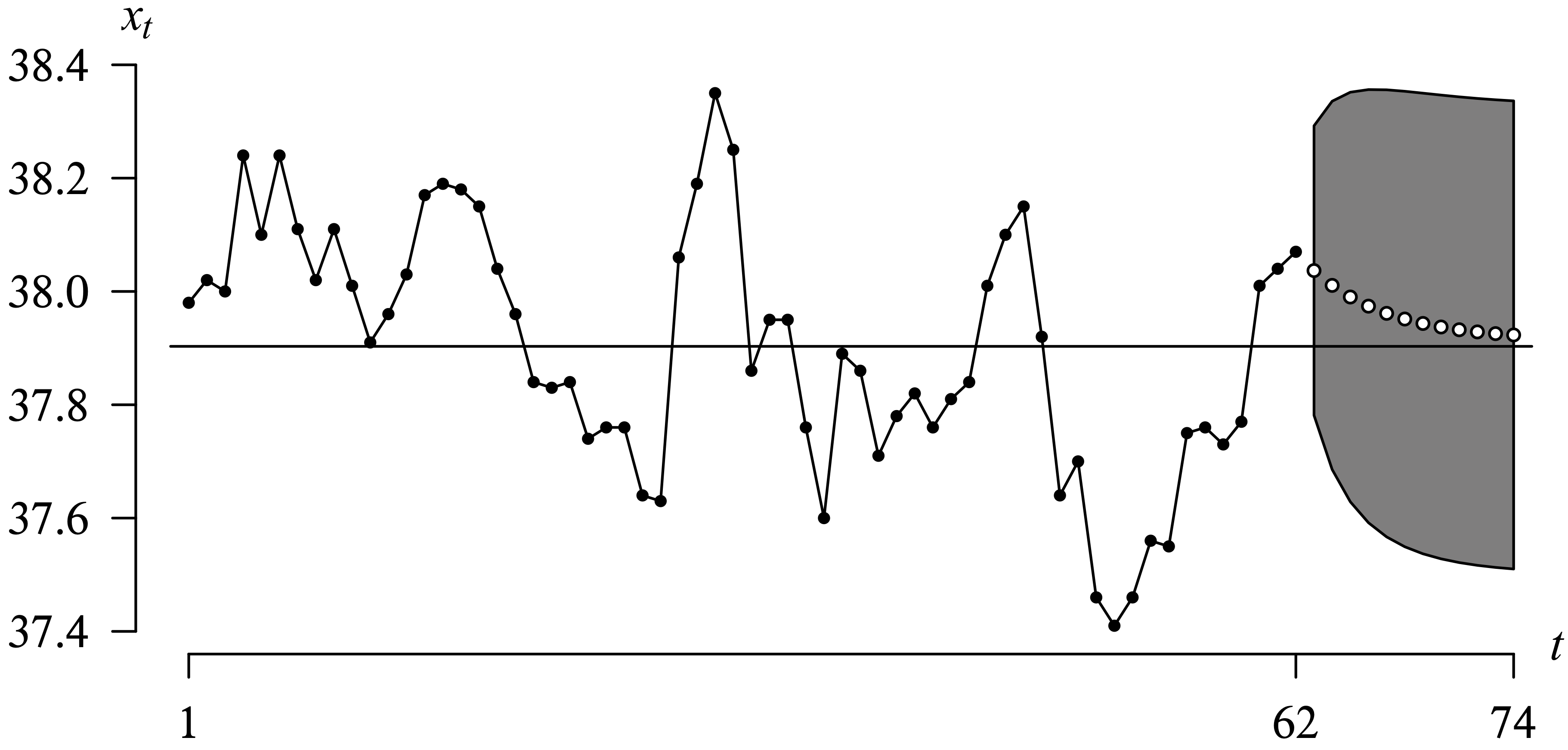
Long Description for Figure 9.11
In the time series plot, the horizontal axis t ranges from 1 to 62. The vertical axis x subscript t ranges from 37.4 to 38.4 in increments of 0.2 degrees Celsius. A horizontal line is drawn at 37.9 degrees Celsius. The graph behaves in a spike manner with solid dots for the first 62 t values. The first 19 values lie above the horizontal line, ranging between 37.9 and 38.2 degrees Celsius. The next eight values decrease from 37.8 to 37.6 degrees Celsius and increase to a peak o 38.4 degrees Celsius at t equals 30. It then decreases below the horizontal line and the next 10 values ranging between 37.6 and 37.8 degrees Celsius, and again increases to 38.1. It then decreases to a minimum temperature o 37.4 degrees at t equals 52, and increases to 38.05 at t equals 62. From t equals 63 to 74, there are open circles following a decreasing trend, approaching 37.9 degrees Celsius. The prediction interval for t-values 63 to 74 ranges between 37.6 and 38.3, and the region is shaded. All data are estimated.
This subsection has introduced the AR(1) time series model. The key results for an AR(1) model are listed below.
- The standard AR(1) model can be written algebraically and with the backshift operator B as
where [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex] and [latex]\sigma _ Z ^ {\, 2} > 0[/latex].
- The shifted AR(1) model can be written algebraically and with the backshift operator B as
- The AR(1) model is always invertible; the AR(1) model is stationary for [latex]-1 < \phi < 1[/latex].
- The stationary shifted AR(1) model can be written as an MA(∞) model for [latex]-1 < \phi < 1[/latex] as
- The AR(1) population autocorrelation function is [latex]\rho(k) = \phi ^ k[/latex] for [latex]-1 < \phi < 1[/latex] and [latex]k = 1, \, 2, \, \ldots[/latex].
- The AR(1) population partial autocorrelation function at lag one is [latex]\rho ^ * (1) = \phi[/latex] for [latex]-1 < \phi < 1[/latex] and [latex]\rho ^ * (k) = 0[/latex] for [latex]k = 2, \, 3, \, \ldots[/latex].
- The three parameters in the shifted AR(1) model, μ, [latex]\phi[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex], can be estimated from a realization of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] by the method of moments, least squares, and maximum likelihood. The point estimators for μ, [latex]\phi[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] are denoted by [latex]\hat \mu[/latex], [latex]\hat \phi[/latex], and [latex]\hat{\sigma} _ Z ^ {\, 2}[/latex], and are typically paired with asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence intervals.
- The forecast value [latex]\hat{X} _ {n + h} = \hat \mu + \hat \phi ^ h \left( x_n - \hat{\mu} \right)[/latex] for an AR(1) model approaches [latex]\hat \mu = \bar x[/latex] as [latex]h \rightarrow \infty[/latex]. The associated prediction intervals have widths that increase as h increases and approach a limit as the time horizon [latex]h \rightarrow \infty[/latex].
If the time series of interest is the daily high temperatures in July in Tuscaloosa, then an AR(1) model would be appropriate if tomorrow’s daily high temperature (Xt) can be modeled as a linear function of
- today’s high temperature ([latex]X_{t-1}[/latex]), and
- a random shock (Zt).
But what if weather had more of a memory than just one day? What if tomorrow’s daily high temperature (Xt) is better modeled as a linear function of
- today’s high temperature ([latex]X_{t-1}[/latex]),
- yesterday’s high temperature ([latex]X_{t-2}[/latex]), and
- a random shock (Zt).
This is an example of the thinking that lies behind the AR(2) model, which is introduced in the next section.
9.1.2 The AR(2) Model
The second-order autoregressive model, denoted by AR(2), can be used for modeling a stationary time series in instances in which the current value of the time series is a linear combination of the two previous values plus a random shock. The mathematics associated with the AR(2) model is somewhat more difficult than that associated with the AR(1) model.
There are three parameters that define an AR(2) model: the real-valued coefficients [latex]\phi_1[/latex] and [latex]\phi_2[/latex], and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. The AR(2) model can be written more compactly in terms of the backshift operator B as
where [latex]\phi(B)[/latex] is the second-order polynomial
The AR(2) model has the form of a multiple linear regression model with two independent variables and no intercept term. The current value Xt is modeled as a linear combination of the two previous values of the time series, [latex]X_{t-1}[/latex] and [latex]X_{t - 2}[/latex], plus a white noise term. The parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex] control the inclination of the regression plane in three-dimensional space. The parameter [latex]\sigma _ Z ^ {\, 2}[/latex] reflects the magnitude of the dispersion of the time series values from the regression plane.
To illustrate the thinking behind the AR(2) model in a specific context, let Xt represent the annual return of a particular stock market index in year t. The AR(2) model indicates that the annual return in year t equals [latex]\phi_1[/latex] multiplied by the previous year’s annual return ([latex]\phi_1 X_{t - 1}[/latex]), plus [latex]\phi_2[/latex] multiplied by the annual return two years prior ([latex]\phi_2 X_{t - 2}[/latex]), plus the year t random white noise term Zt.
Stationarity
Theorem 8.3 indicates that all AR(2) models are invertible, but are stationary when the roots of
lie outside of the unit circle in the complex plane. Let B1 and B2 denote these two roots. Using the quadratic equation, the two roots are
Since [latex]\phi(B_1) = \phi(B_2) = 0[/latex], the quadratic function [latex]\phi(B)[/latex] can also be written in factored form as
Equating the two versions of [latex]\phi(B)[/latex] above and matching coefficients results in
These two equations define the mapping from the complex plane, which contains the roots B1 and B2, to the plane that contains the AR(2) parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex]. To find the stationary region, we must find the mapping of the part of the complex plane outside of the unit circle to the [latex](\phi_1, \, \phi_2)[/latex] plane. The mapping yields a triangular-shaped stationary region, as specified in the following result.
Population Autocorrelation Function
Now that the stationary region for an AR(2) time series model has been established, we turn to the derivation of the population autocorrelation function. Assuming that the parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex] fall in the stationary region, the AR(2) model
can be multiplied by [latex]X_{t - k}[/latex] to give
Taking the expected value of both sides of this equation results in the recursive equation
for [latex]k = 1, \, 2, \, \ldots[/latex] because Zt has expected value zero and is independent of [latex]X_{t - k}[/latex]. Dividing both sides of this equation by [latex]\gamma(0) = V \left[ X_t \right][/latex] gives the recursive equation
for [latex]k = 1, \, 2, \, \ldots[/latex]. These linear equations, whether written in terms of [latex]\gamma(k)[/latex] or [latex]\rho(k)[/latex], are known in time series analysis as the Yule–Walker equations after British statisticians George Udny Yule and Sir Gilbert Walker. Once the first two values of [latex]\gamma(k)[/latex] or [latex]\rho(k)[/latex] are known, these recursive equations can be used to calculate subsequent values. The next two paragraphs focus on determining the first two values of [latex]\gamma(k)[/latex] and [latex]\rho(k)[/latex], respectively.
For a stationary AR(2) time series model, we derive expressions for [latex]\gamma(0)[/latex] and [latex]\gamma(1)[/latex]. The AR(2) model is
Squaring both sides of this equation and taking the expected value of both sides gives
Using the symmetry of the population autocovariance function, the Yule–Walker equation with [latex]k = 1[/latex] is
Replacing this expression for [latex]\gamma(1)[/latex] in the previous equation gives
Moving all terms involving [latex]\gamma(0)[/latex] to the left-hand side of this equation gives
Solving this equation for [latex]\gamma(0)[/latex],
An expression for [latex]\gamma(1)[/latex] is
These two values can be used as arguments in the Yule–Walker equations to obtain subsequent values for [latex]\gamma(k)[/latex].
We now turn to the problem of finding [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex]. The first two Yule–Walker equations in terms of [latex]\rho(k)[/latex] are
Since [latex]\rho(0) = 1[/latex] and [latex]\rho(-k) = \rho(k)[/latex] via Theorem 7.1, these equations reduce to
which are easily solved for [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex]:
A general formula for [latex]\rho(k)[/latex] exists, but it can involve complex numbers and is unwieldy. An exercise concerning its calculation is given at the end of the chapter. These results are summarized in the following theorem.
We now focus in on the values of [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex]. We can solve for [latex]\phi_1[/latex] and [latex]\phi_2[/latex] in terms of [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex] as
These equations can be helpful in the three settings described below.
- These equations bear some practical use in that the first two sample autocorrelation function values, r1 and r2, can be calculated from a time series and used as approximations for[latex]\rho(1)[/latex] and [latex]\rho(2)[/latex], yielding estimates for [latex]\phi_1[/latex] and [latex]\phi_2[/latex]. These can in turn be used as initial estimates for finding point estimates for [latex]\phi_1[/latex] and [latex]\phi_2[/latex] by, for example, least squares or maximum likelihood estimation, should numerical methods be required.
- Level surfaces (that is, contours) in the triangular-shaped stationary region from Theorem 9.9 can be determined by fixing values of [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex]. As an illustration, consider [latex]\rho(1) = 0[/latex]. In this case [latex]\phi_1 = 0[/latex] and [latex]\phi_2 = \rho(2)[/latex], which is a line segment in the stationary region. Continuing in this fashion for several fixed values of [latex]\rho(1)[/latex] [with varying values of [latex]\rho(2)[/latex]] and then for several fixed values of [latex]\rho(2)[/latex] [with varying values of [latex]\rho(1)[/latex]] results in the graph of the stationary region with the level surfaces included shown in Figure 9.13. The level surfaces associated with fixed values of [latex]\rho(1)[/latex] are lines; the level surfaces associated with fixed values of [latex]\rho(2)[/latex] are curves.
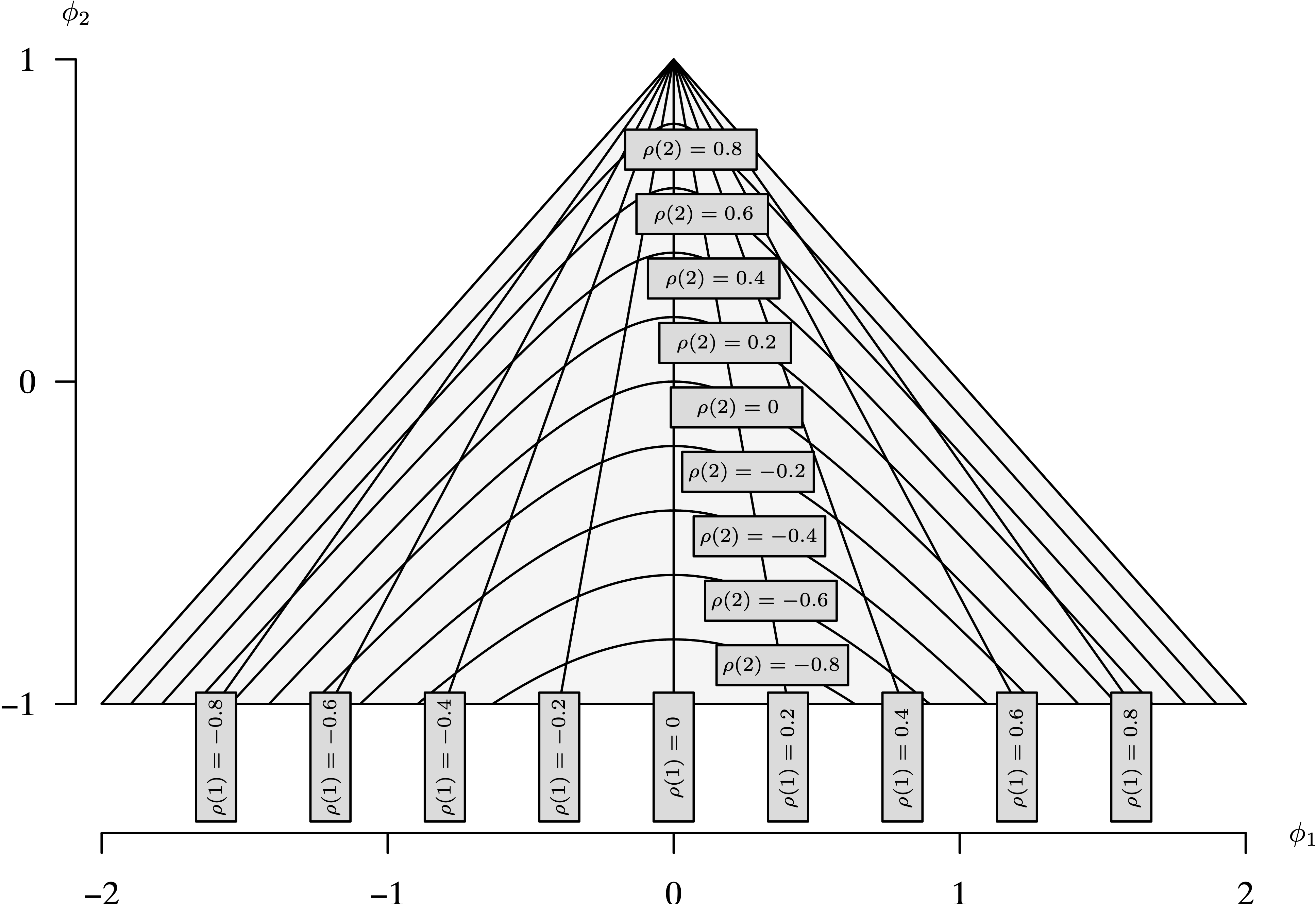
Figure 9.13: Stationary region for an AR(2) time series model with level surfaces. Long Description for Figure 9.13
The horizontal axis measures phi 1 and ranges from negative 2 to 2 in increments of 1 unit. The vertical axis measures phi 2, and ranges from negative 1 to 1 in increments of 1 unit. A triangle is drawn with the apex (0, 1), and the bottom vertices (negative 2, negative 1) and (2, negative 1). The value rho of 1 equals 0 corresponds to the 0 value of the phi 2 function. The rho of 1 values equals 0.2 and 0.4 lies between phi values negative 1 and 0. The rho of 1 values 0.6 and 0.8 lies between phi 1 values negative 1 and negative 2. Similarly, the values of rho lie on the right side of 0. From the apex (0, 1), the triangular surface levels are drawn and meet the horizontal line at each rho of 1 value. Nine concave parabolas are drawn inside the triangular surface levels, each having a maximum at phi 2 value 0. Their maxima are represented by rho of 2 values that range from negative 0.8 to 0.8 in increments of 0.2.
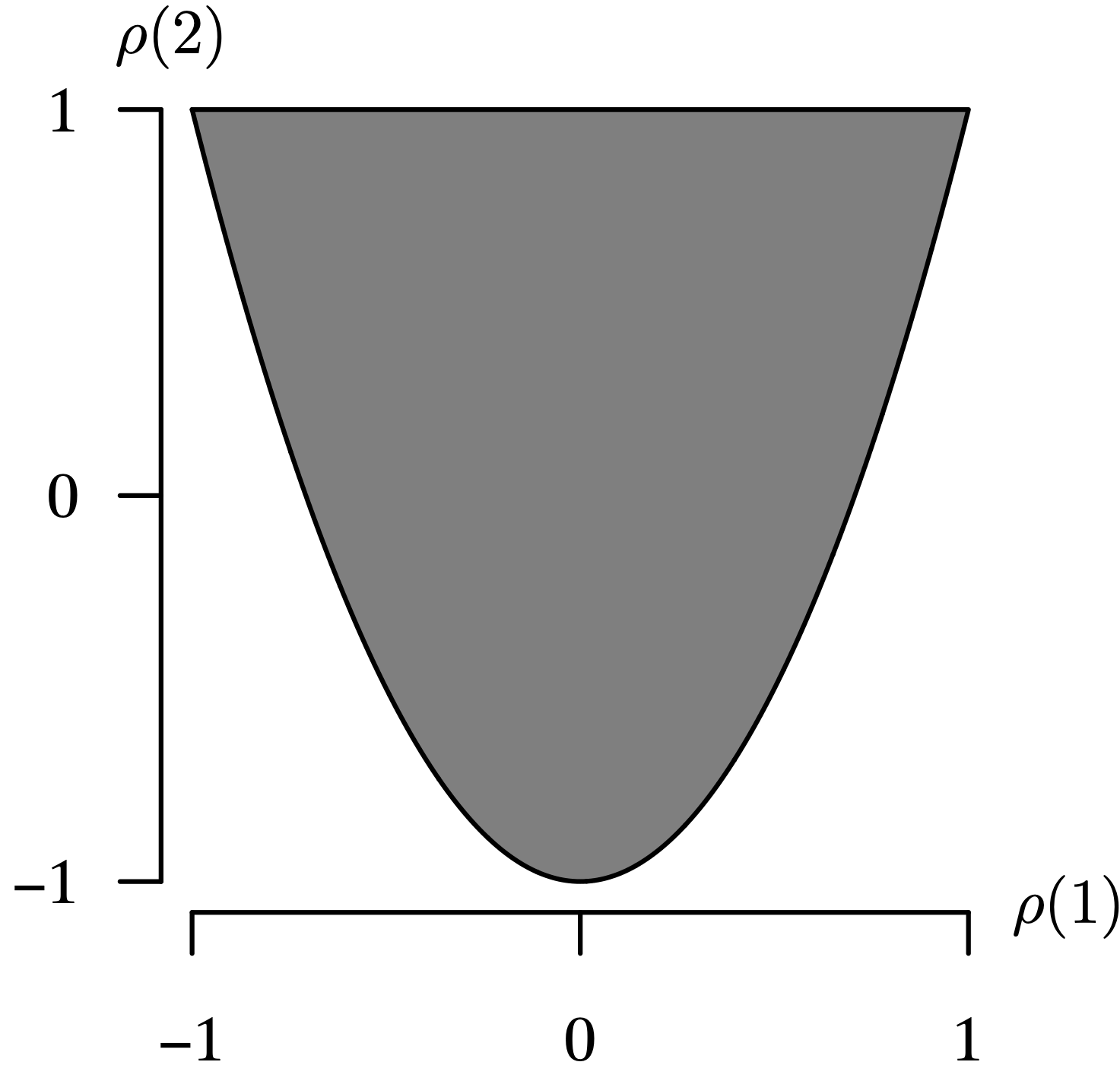
- Since [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex] are population correlations, the obvious constraints on their values for an AR(2) time series model are [latex]-1 < \rho(1) < 1[/latex] and [latex]-1 < \rho(2) < 1[/latex]. Additionally, since [latex]\phi_2 > -1[/latex] in order to fall into the triangular-shaped stationary region defined in Theorem 9.9 for the AR(2) time series model,
The boundary of this third constraint is a parabola in the [latex]\big( \rho(1), \, \rho(2) \big)[/latex] plane. The shaded region in Figure 9.14 shows the [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex] values that are associated with stationary AR(2) time series models. Unlike the AR(1) population autocorrelation function, it is possible to achieve a stationary model with [latex]|\rho(2)| > |\rho(1)|[/latex]. The AR(2) population autocorrelation function values are not necessarily monotonically decreasing in magnitude as they were in the AR(1) model.
Population Partial Autocorrelation Function
We now determine the population partial autocorrelation function for an AR(2) model. Using Definition 7.4, the population lag 0 partial autocorrelation is [latex]\rho ^ * (0) = 1[/latex]. The population lag 1 partial autocorrelation is [latex]\rho ^ * (1) = \rho (1) = \phi_1 / (1 - \phi_2)[/latex]. After evaluating the determinants and simplifying, the population lag 2 partial autocorrelation is
Appealing to the Yule–Walker equations from Theorem 9.10 to define the third column of the determinant of the numerator, the population lag 3 partial autocorrelation is
The determinant in the numerator is zero because the third column is a linear combination of the first two columns. This pattern continues for the higher lags. When computing [latex]\rho^*(k)[/latex] for [latex]k = 3, \, 4, \, \ldots ,[/latex] the first, second, and last columns of the matrix in the numerator are
The last column of the matrix in the numerator is a linear combination of the first two columns. The matrix in the numerator of the calculation of [latex]\rho ^ * (k)[/latex] is singular, which means that its determinant is zero. This constitutes a proof of the following result.
The population partial autocorrelation function for the AR(2) model cuts off after lag 2. A graph of the sample partial autocorrelation function (that is, a graph of [latex]r^*_k[/latex] for the first few values of k), should also cut off after lag 2 if the AR(2) model is appropriate. This sample partial autocorrelation function shape is easier to recognize than the associated sample autocorrelation function shape because cutting off is easier to recognize than tailing off in the presence of random sampling variability.
A careful inspection of Theorem 9.11 reveals that the signs of [latex]\phi_1[/latex] and [latex]\phi_2[/latex] match the signs of [latex]\rho^*(1)[/latex] and [latex]\rho^*(2)[/latex], respectively:
for [latex]\phi_1[/latex] and [latex]\phi_2[/latex] falling in the triangular-shaped stationary region. Figure 9.15 shows the stationary region from Theorem 9.9, along with plots of the representative population autocorrelation function and population partial autocorrelation function. There are four points, one in each quadrant, that are plotted. The population autocorrelation function and the population partial autocorrelation function associated with those four points are plotted in each of the quadrants. As expected, the signs of the values of and [latex]\phi_1[/latex] and [latex]\rho^*(1)[/latex] match and the signs of the values of [latex]\phi_2[/latex] and [latex]\rho^*(2)[/latex] match. The quadrant in the stationary region determines the signs of [latex]\rho^*(1)[/latex] and [latex]\rho^*(2)[/latex], as illustrated by the four representative population partial autocorrelation functions graphed in Figure 9.15. As you can see by inspecting the shapes of [latex]\rho(k)[/latex] and [latex]\rho^*(k)[/latex] from Figure 9.15, the addition of the parameter ϕ2 in the transition from the AR(1) model to the AR(2) model results in significant additional modeling capability. The following observations can be gleaned from Figure 9.15.
-
- As expected, all population partial autocorrelation functions cut off after lag two.
- When [latex]\phi(B)[/latex] has real roots, the population autocorrelation function consists of mixtures of damped exponentials.
-
- When [latex]\phi(B)[/latex] has complex roots, the population autocorrelation function has a damped sinusoidal shape.
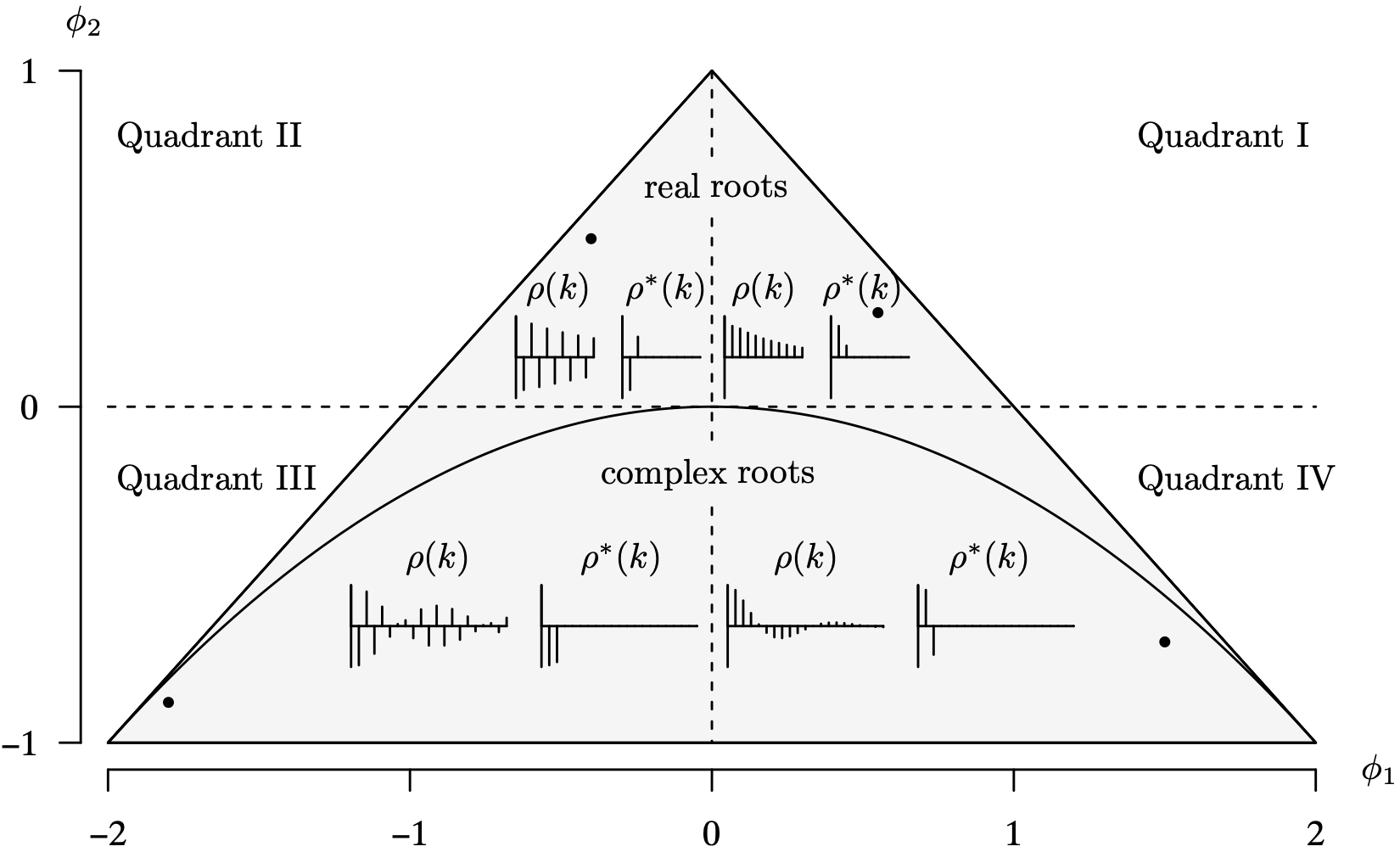
Long Description for Figure 9.15
The horizontal axis phi 1 ranges from negative 2 to 2 in increments of 1 unit. The vertical axis phi 2 ranges from negative 1 to 1 in increments of 1 unit. A triangle is drawn on the plane with the vertices (negative 2, negative 1), (0, 1), and (2, negative 1). A concave down parabola begins from (negative 2, negative 1), reaches a maximum at (0, 0), and decreases to (2, negative 1). A point is plotted in each of the four quadrants. The real roots lie above the parabola region inside the triangular region in quadrants 1 and 2. In quadrant 1, the rho of k values decreases progressively. The rho star of k has two decreasing positive values. In quadrant 2, the rho of k values alternates between positive and negative with decreasing magnitude. The rho star of k values alternates between positive and negative. The complex roots lie in the parabolic region in quadrants 3 and 4. In quadrant 3, the rho of k follows a damped sinusoidal fashion and the rho star of k has negative values for the first three k values. In quadrant 4, the rho of k values follows a damped sinusoidal fashion. The rho star of k has a positive and a negative value.
The population autocorrelations on the tiny inset plots of [latex]\rho(k)[/latex] and [latex]\rho^*(k)[/latex] in Figure 9.15 can be calculated using the recursive relationships from Theorem 9.10 [for [latex]\rho(k)[/latex]] and Theorem 9.11 [for [latex]\rho^*(k)[/latex]]. They can also be calculated using the R ARMAacf function. Consider the two inset plots in the fourth quadrant of the graph in Figure 9.15, for example, that correspond to [latex]\phi_1 = 1.5[/latex] and [latex]\phi_2 = -0.7[/latex]. The graph of the first 20 lags of [latex]\rho(k)[/latex] can be plotted with the R command
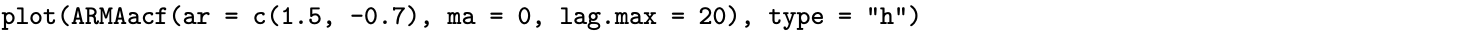
Likewise, the graph of the first 20 lags of [latex]\rho^*(k)[/latex] can be plotted with
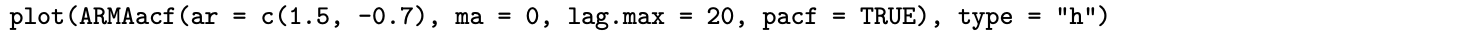
The ar argument defines the [latex]\phi_1[/latex] and [latex]\phi_2[/latex] parameters of the AR(2) model, the ma argument is set to zero to indicate that there are no moving average terms in the AR(2) model, the lag.max argument is set to 20 to return the first 20 autocorrelations, and the type argument in the call to plot is set to "h" in order to graph the autocorrelations as spikes rather than points.
As was the case with the AR(1) time series model, the AR(2) time series can be written as an MA(∞) time series model. This alternative representation can be useful for deriving certain quantities associated with the AR(2) model, in particular, standard errors of forecasted values. The first form of a general linear model, which is equivalent to an MA(∞) model, is
Our goal is to determine the values of θ1, θ2, … that correspond to fixed parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex]. Since the MA(∞) model is valid at time t, it is also valid at times [latex]t-1[/latex] and [latex]t-2[/latex]:
and
So the AR(2) time series model
as established in Definition 9.2, can be rewritten as
Equating the coefficients of [latex]Z_{t - 1}[/latex] gives
Equating the coefficients of [latex]Z_{t - 2}[/latex] gives
Equating the coefficients of [latex]Z_{t - k}[/latex] gives the recursive equation
for [latex]k = 3, \, 4, \, \ldots[/latex].
An exercise at the end of the chapter highlights other methods for calculating the coefficients θ1, θ2, … in the MA(∞) model which is equivalent to the stationary AR(2) model.
The Shifted AR(2) Model
For a stationary AR(2) model expressed as an MA(∞) model, it is clear that [latex]E \left[ X_t \right] = 0[/latex]. This model is not of much use in practice because most real-world time series are not centered around zero. Adding a shift parameter μ overcomes this shortcoming. Since population variance and covariance are unaffected by a shift, the associated population autocorrelation and partial autocorrelation functions remain the same as those given in Theorems 9.10 and 9.11.
The shifted AR(2) model can be written in terms of the backshift operator B as
where [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B^2[/latex]. The practical problem of fitting a shifted AR(2) model to an observed time series of n values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] will be illustrated later in this subsection.
Simulation
An AR(2) time series can be simulated by appealing to the defining formula for the AR(2) model. Iteratively applying the defining formula for a standard AR(2) model
from Definition 9.2 results in the simulated values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. The primary difficult aspect of devising a simulation algorithm is generating the first two values, X1 and X2. For simplicity, assume that the white noise terms are Gaussian white noise terms. There are two approaches to overcome this initialization problem. The first approach generates X1 and X2 from a bivariate normal distribution with population mean vector [latex]\boldsymbol{0} = (0, \, 0) ^ \prime[/latex] and variance–covariance matrix
via Theorem 9.10. Notice that in the special case of [latex]\phi_1 = \phi_2 = 0[/latex] this matrix reduces to the variance–covariance matrix for Gaussian white noise, which is [latex]I \sigma _ Z ^ {\, 2}[/latex]. The algorithm given as pseudocode below generates initial time series observations X1 and X2 as indicated above, and then uses an additional [latex]n - 2[/latex] Gaussian white noise terms [latex]Z_3, \, Z_4, \, \ldots, \, Z_n[/latex] to generate the remaining time series values [latex]X_3, \, X_4, \, \ldots, \, X_n[/latex] using the AR(2) defining formula from Definition 9.2. Indentation denotes nesting in the algorithm.
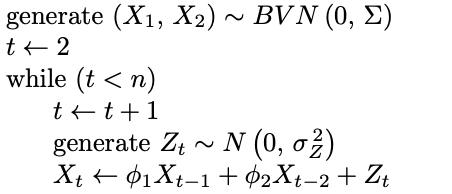
The four-parameter shifted AR(2) time series model which includes a population mean parameter μ can be simulated by simply adding μ to each time series observation generated by this algorithm. The next example implements this algorithm in R.
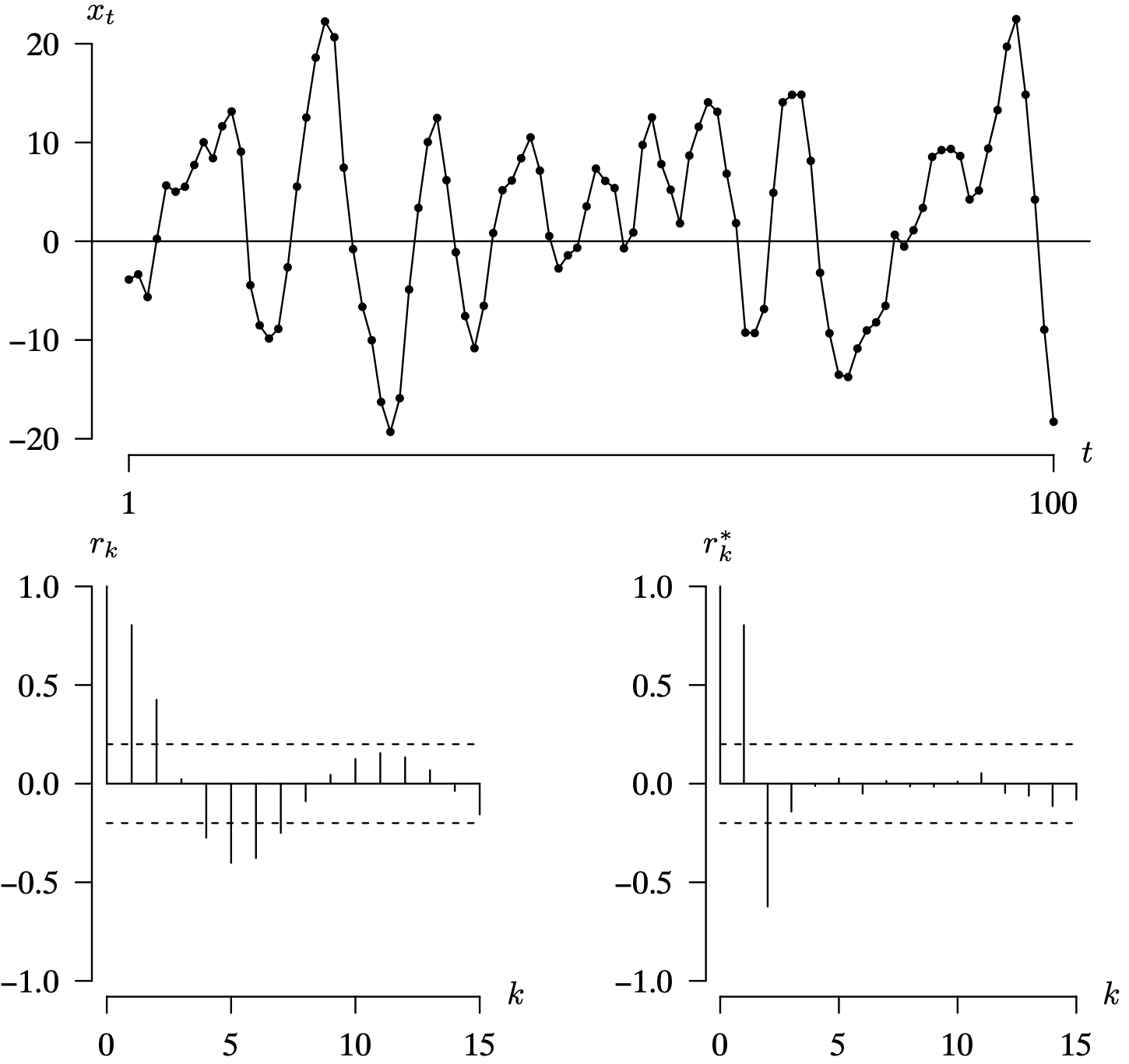
Long Description for Figure 9.16
In the time series plot, the horizontal axis t ranges from 1 to 100. The vertical axis x subscript t ranges from negative 20 to 20 in increments of 10 units. A horizontal line is drawn at 0. The data forms a spike pattern, beginning below the horizontal line around x subscript t equals negative 5. It increases progressively to an x subscript value of 13 at t equals 12, then decreases to negative 10 at t equals 16. It increases to a peak of 22 at t equals 22, decreases to the lowest point of negative 20 at t equals 29, and then oscillates between x subscript t values of negative 15 and 15 until t equals 78. It finally reaches the highest point of 21 at t equals 96, and decreases to negative 20 at t equals 100. In the first correlogram, the horizontal axis k ranges from 0 to 15 in increments of 1 unit. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A solid horizontal line is drawn at 0.0. Two dashed horizontal lines are drawn at x subscript t values of negative 0.2 and 0.2. The values of the r subscript follow a damped sinusoidal fashion. The first four values are positive, decreasing from 1.0 to 0.02, the next five values are negative, ranging between negative 0.4 and 0.0. The next five values are positive and follow a bell shape, ranging between 0.0 and 0.2, and the last two values are negative 0.02 and negative 0.2. In the second correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r star subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A solid horizontal line is drawn at 0.0. The first four values of the r star subscript k for k values 0 to 4 are 1.0, 0.8, negative 0.6, and negative 0.15, respectively. The remaining r subscript k values range between negative 0.15 and 0.1. All data are estimated.
We recommend running the simulation code from the previous example several dozen times in a loop and viewing the associated plots of xt, rk, and [latex]r_k^*[/latex] in search of patterns. This will allow you to see how various realizations of a simulated AR(2) time series model vary from one realization to the next. So when you then view a single realization of a real-life time series, you will have a sense of how far these plots might deviate from their expected patterns.
There is a second way to overcome the initialization problem in simulating observations from an AR(2) time series. This second technique starts the time series with two initial arbitrary values, and then allows the time series to “warm up” or “burn in” for several time periods before producing the first observation X1. Reasonable initial arbitrary values for the standard AR(2) model are 0; reasonable initial arbitrary values for the shifted AR(2) model are μ. This is the approach taken by the built-in R function named arima.sim, which simulates a realization of a time series. Using the arima.sim function saves a few keystrokes over the approach taken in the previous example, as illustrated next.
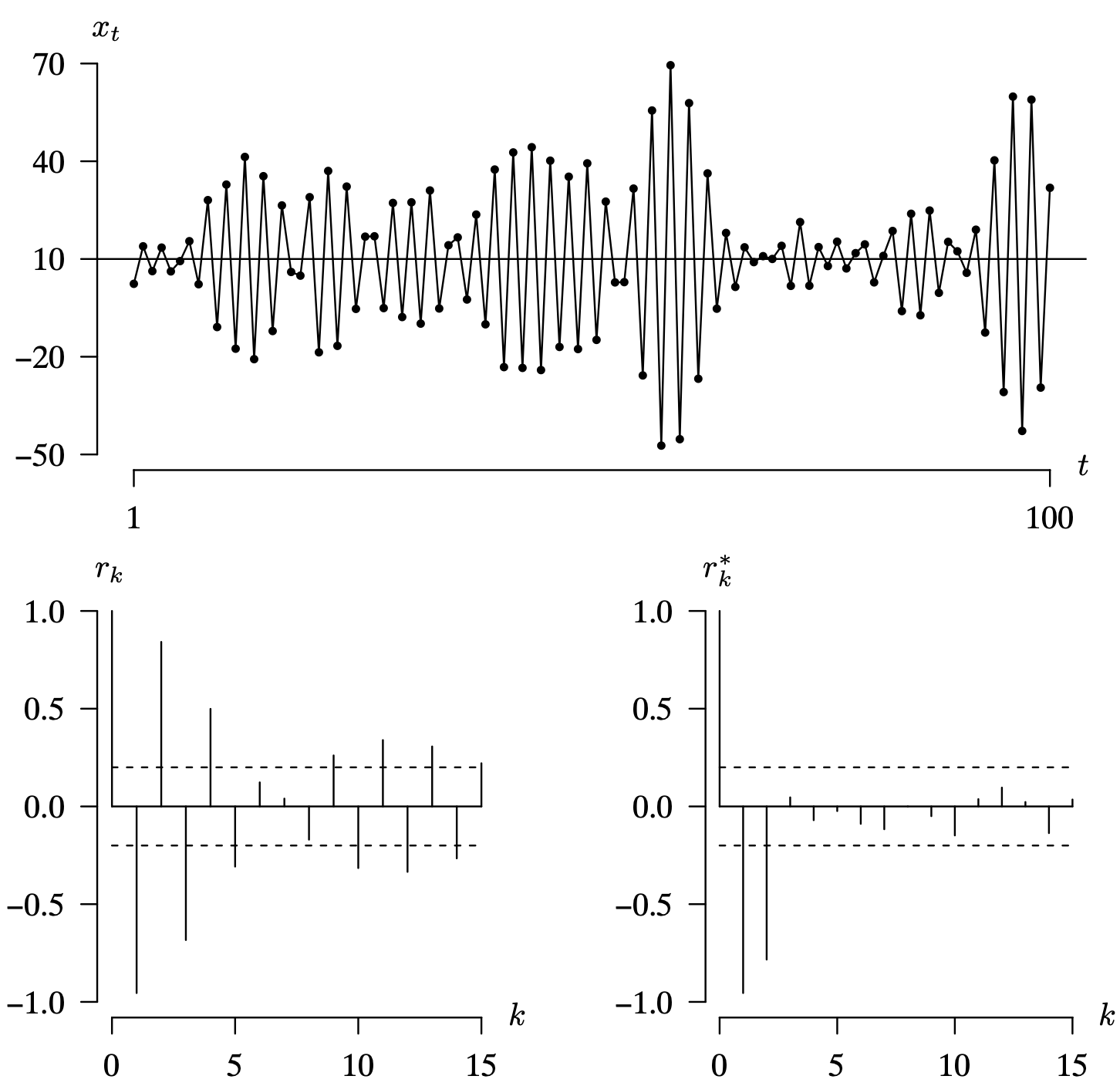
Long Description for Figure 9.17
In the time series plot, the horizontal axis t ranges from 1 to 100. The vertical axis x subscript t ranges from negative 50 to 70 in increments of 30 units. A horizontal line is drawn at 0. The data forms a spike pattern, alternating above and below the horizontal line. The first 54 x subscript t values vacillate between negative 20 and 40, reach a peak of 70 at t equals 59, and then decrease. It again fluctuates between the values 5 and 15 for the next few t values and the last 10 values range between negative 50 and 50. In the first correlogram, the horizontal axis ranges from 0 to 15 in increments of 5 units. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A solid horizontal line is drawn at 0.0. Two dashed horizontal lines are drawn at negative 0.2 and 0.2. The r subscript k values alternate between positive and negative with decreasing magnitude. In the second correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r star subscript k ranges from negative 1.0 to 1.0, in increments of 0.5 units. A solid horizontal line is drawn at 0.0. The first r star subscript k values are 1.0, negative 1.0, and negative 0.7 for k values 0, 1, and 2, respectively. The remaining r star subscript k values range between negative 0.2 and 0.1. All data are estimated.
The remaining topics associated with the AR(2) time series model are statistical in nature: parameter estimation, model assessment, model selection, and forecasting. A sample time series that will be revisited throughout these topics is introduced next.
Parameter Estimation
There are four parameters, μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex], to estimate in the shifted AR(2) model
The three parameter estimation techniques outlined in Section 8.2.1, method of moments, least squares, and maximum likelihood estimation, are applied to the shifted AR(2) time series model next.
Approach 1: Method of moments. In the case of estimating the four parameters in the shifted AR(2) model by the method of moments, we match the population and sample (a) first-order moments, (b) second-order moments, (c) lag 1 autocorrelation, and (d) lag 2 autocorrelation. Placing the population moments on the left-hand side of the equation and the associated sample moments on the right-hand side of the equation results in four equations in four unknowns:
The expected value of Xt is μ, the expected value of [latex]X_t^2[/latex] can be found by using the shortcut formula for the population variance and by using the value of [latex]\gamma(0) = V[X_t][/latex] from Theorem 9.10, and the values of [latex]\rho(1)[/latex] and [latex]\rho(2)[/latex] are also obtained from Theorem 9.10. So the four equations become
Solving these equations for the four unknown parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex] and [latex]\sigma _ Z ^ {\, 2}[/latex] yields closed-form solutions for the method of moments estimators
This constitutes a proof of the following result.
These estimators are random variables and have been written as a function of the random time series values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. For observed time series values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], the lowercase versions of the formulas will be used. These estimators are often known as the Yule–Walker estimators because their derivation involved the Yule–Walker equations from Theorem 9.10.
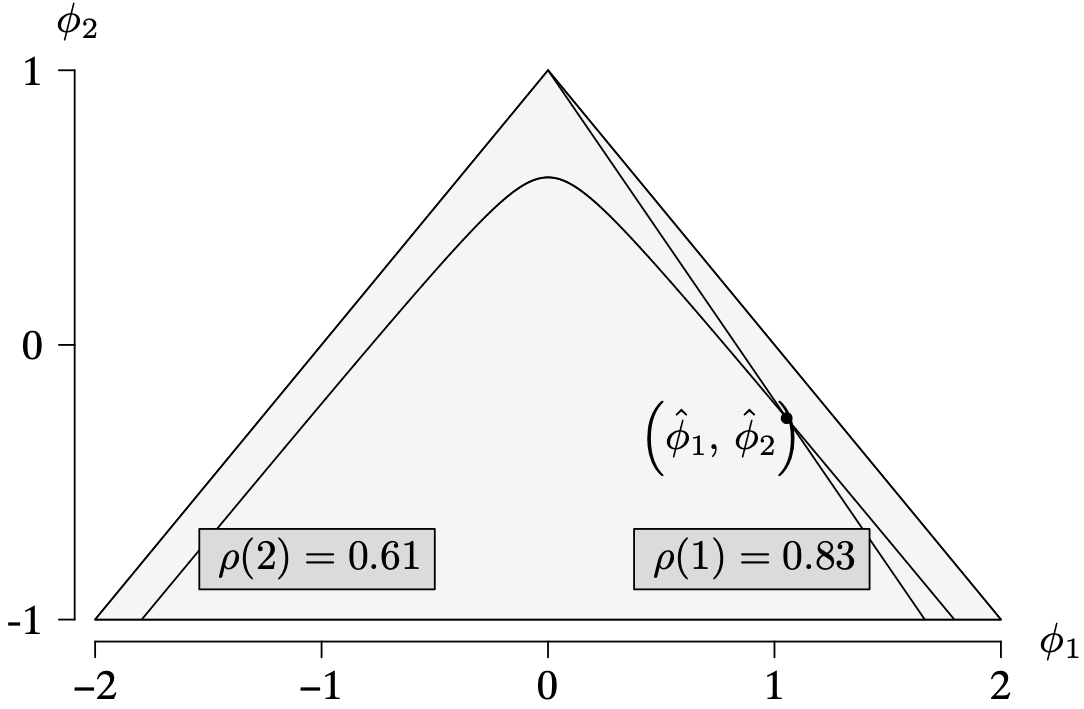
Long Description for Figure 9.20
The horizontal axis phi 1 ranges from negative 2 to 2 in increments of 1 unit. The vertical axis phi 2 ranges from negative 1 to 1 in increments of 1 unit. A triangle is drawn on the plane, with the vertices (negative 2, negative 1), (0, 1), and (2, negative 1). A concave parabolic surface is drawn inside the triangular area, with the highest point at (0, 0.5). The point (phi 1 cap, phi 2 cap) is plotted on the parabola at (1.05, negative 0.6). Another line is drawn from the peak (0, 1) of the triangle, and intersects the parabola at (phi 1 cap, phi 2 cap). The line associated with rho of 1 is 0.83 and the parabola associated with rho of 2 is 0.61. All data are estimated.
Approach 2: Least squares. Consider the shifted stationary AR(2) model
For least squares estimation, we first establish the sum of squares S as a function of the parameters μ, [latex]\phi_1[/latex], and [latex]\phi_2[/latex]. This time, however, we forgo the calculus and leave the optimization to the R optim function in order to find the least squares estimators of μ, [latex]\phi_1[/latex], and [latex]\phi_2[/latex]. Once these least squares estimators have been determined, the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex] will be estimated.
The sum of squared errors is
If this derivation were being done by hand, we would now calculate the partial derivatives of S with respect to the unknown parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], equate them to zero and solve. As was the case with the AR(1) model, there is no closed-form solution, so numerical methods are required to calculate the parameter estimates. In the example that follows, we will use the optim function in R to determine the least squares parameter estimates that minimize S.
The last parameter to estimate is [latex]\sigma _ Z ^ {\, 2}[/latex]. Since
from Theorem 9.10 for an AR(2) time series model, the population variance of the white noise can be expressed as
Replacing [latex]\phi_1[/latex] and [latex]\phi_2[/latex] by their least squares estimators [latex]\hat \phi_1[/latex] and [latex]\hat \phi_2[/latex], respectively, and replacing the lag 0 autocovariance [latex]{\gamma(0) = V \left[ X_t \right]}[/latex] by its estimator [latex]c_0 = \frac{1}{n} \sum_{t\,=\,1}^n \left( X_t - \bar X \right) ^ 2[/latex] gives the estimator
This derivation constitutes a proof of the following result.
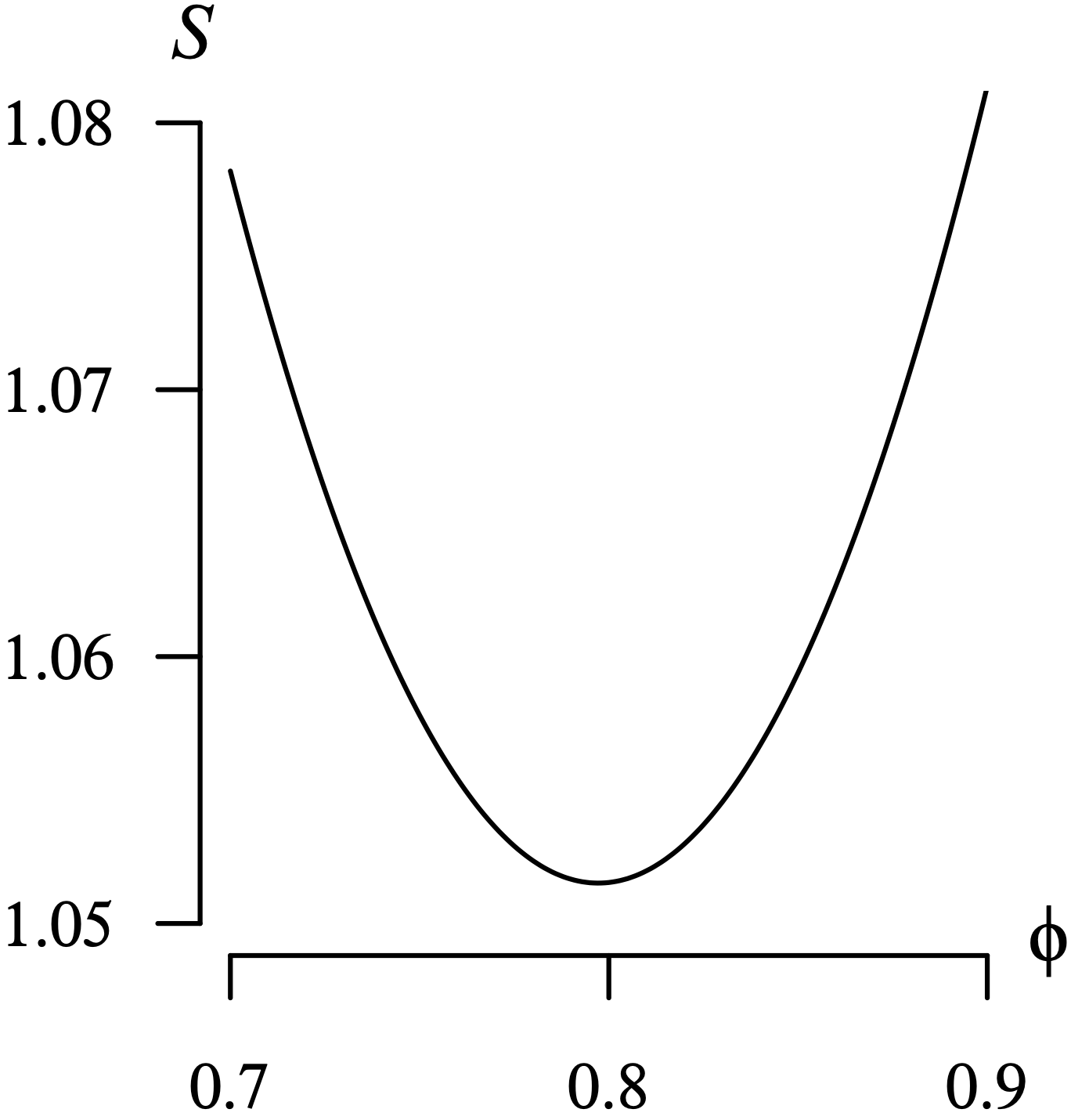
We now use numerical methods to find the least squares estimates for the unknown parameters in the AR(2) time series model for the Lake Huron time series from Example 9.14.
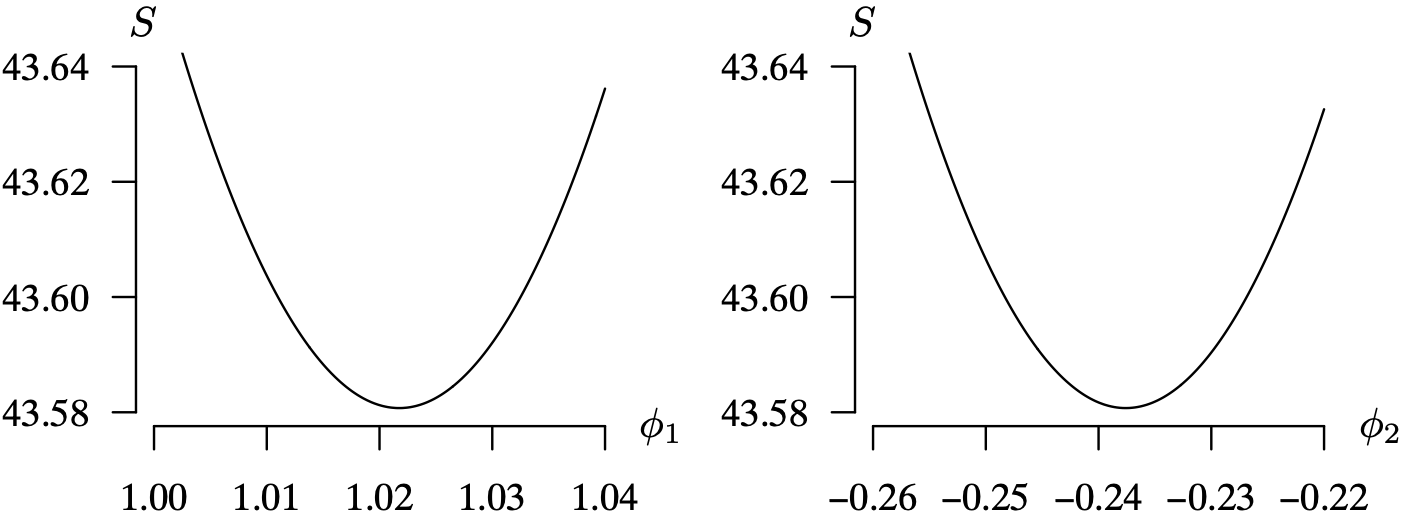
Long Description for Figure 9.21
The first graph shows the function of phi 1. The horizontal axis phi 1 ranges from 1.00 to 1.04 in increments of 0.01 units. The vertical axis S ranges from 43.58 to 43.64 in increments of 0.02 units. The convex parabola decreases from (1.00, 43.64), reaches a low point at (1.02, 43.58), and increases to (1.04, 43.64). The second graph shows the function of phi 2. The horizontal axis ranges from negative 0.26 to negative 0.22 and ranges from 0.01 units. The vertical axis S ranges from 43.58 to 43.64 in increments of 0.02 units. The convex parabola decreases from (negative 0.26, 43.64), reaches a low point at (negative 0.24, 43.58), and increases to (negative 0.22, 43.63). All data are estimated.
Approach 3: Maximum likelihood estimation. The procedure for determining the maximum likelihood estimators for the unknown parameters in an AR(2) time series model follows along the same lines as in the AR(1) time series model from the previous section. Once again, to use maximum likelihood estimation, we must assume that the random shocks from the white noise are Gaussian white noise, with associated probability density function
for [latex]t = 1, \, 2, \, \ldots, \, n[/latex]. Determining the likelihood function, which is the joint probability density function of the observed values in the time series [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex], involves finding
where the [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] arguments on L and the μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _Z ^ {\, 2}[/latex] arguments on f have been dropped for brevity. As before, it is not possible to simply multiply the marginal probability density functions because the values in the AR(2) time series model are correlated. As in the case of an AR(1) model, we use the transformation technique to find the conditional joint probability density function of [latex]X_3, \, X_4, \, \ldots, \, X_n[/latex] conditioned on [latex]X_1 = x_1[/latex] and [latex]X_2 = x_2[/latex], which is denoted by
for [latex]\left( x_3, \, x_4, \, \ldots, \, x_n \right) \in {\cal R} ^ {n - 2}[/latex]. This conditional joint probability density function is multiplied by the marginal joint probability density function of X1 and X2 (which has the bivariate normal distribution) resulting in a joint probability density function of [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]:
for [latex]\left( x_1, \, x_2, \, \ldots, \, x_n \right) \in {\cal R} ^ n[/latex]. This function serves as the likelihood function, which should be maximized with respect to the unknown parameters [latex]\mu[/latex], [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex]. One can easily imagine how complicated this expression is, based on the values of [latex]\gamma(0)[/latex] and [latex]\gamma(1)[/latex] from Theorem 9.10. So we forgo the tedious mathematics and leave the calculations to the ar function in R when determining the maximum likelihood estimates for the parameters in fitting the Lake Huron time series to the shifted AR(2) time series model.
Table 9.6 summarizes the point estimators for the AR(2) model for the Lake Huron time series calculated by the R commands
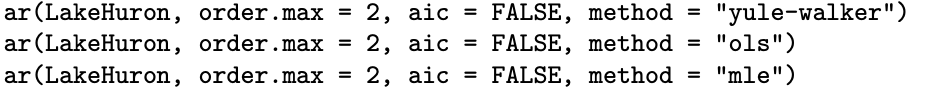
|
Method |
[latex]\hat \mu[/latex] |
[latex]\hat \phi_1[/latex] |
[latex]\hat \phi_2[/latex] |
[latex]\hat \sigma _Z ^ {\, 2}[/latex] |
|---|---|---|---|---|
|
Method of moments (Yule–Walker) |
579.0 |
1.0538 |
[latex]-0.2668[/latex] |
0.5075 |
|
Ordinary least squares |
579.0 |
1.0217 |
[latex]-0.2376[/latex] |
0.4540 |
|
Maximum likelihood estimation |
579.0 |
1.0437 |
[latex]-0.2496[/latex] |
0.4788 |
The point estimators associated with the three methods are quite close for this particular time series. The R function ar fits autoregressive models. There are tiny differences between some of the entries in Table 9.6 and those from Examples 9.15 and 9.16 which might be due to slightly different approximations and/or roundoff in the optimization routines.
The focus on estimation thus far has been on point estimation techniques. We also want to report some indication of the precision associated with these point estimators. The sampling distributions of [latex]\hat \mu[/latex], [latex]\hat \phi_1[/latex], [latex]\hat \phi_2[/latex], and [latex]\hat \sigma _ Z ^ {\, 2}[/latex] in the AR(2) model are too complicated to derive analytically. As an illustration of how to construct an approximate confidence interval for [latex]\phi_1[/latex] or [latex]\phi_2[/latex], we use the asymptotic normality of the maximum likelihood estimator of [latex]\phi_1[/latex] and [latex]\phi_2[/latex] in the following result. The asymptotic variance–covariance matrix associated with the parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex] is
Using just the diagonal elements of this matrix results in the following asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\phi_1[/latex] and [latex]\phi_2[/latex].
These asymptotically exact confidence intervals for [latex]\phi_1[/latex] and [latex]\phi_2[/latex] will now be illustrated for the lake levels from the Lake Huron time series from the previous four examples.
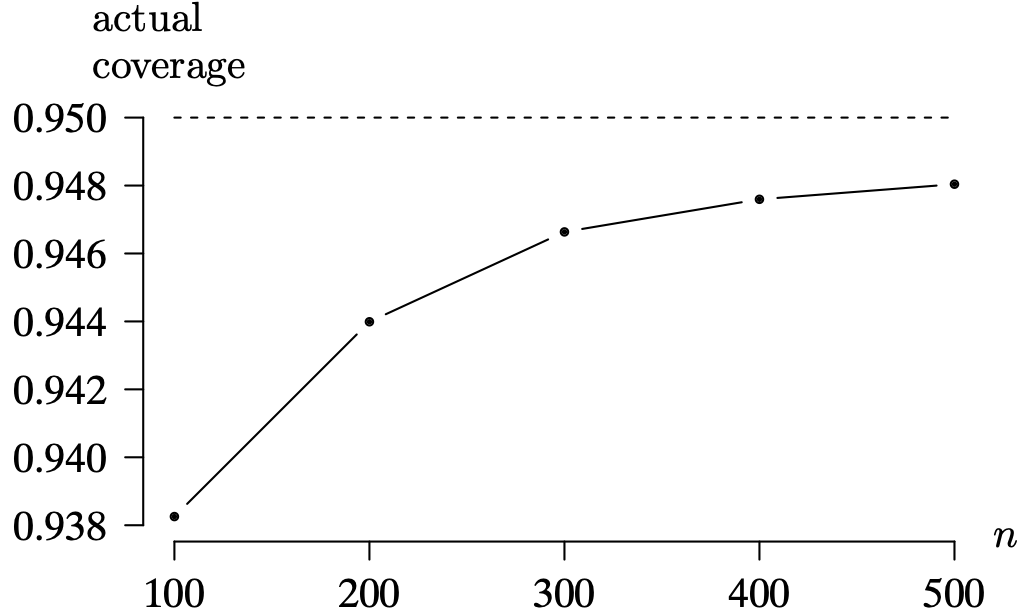
Long Description for Figure 9.22
The horizontal axis n ranges from 100 to 500 in increments of 100 units. The vertical axis measuring actual coverage ranges from 0.938 to 0.950 in increments of 0.002. A dashed horizontal line is drawn at the actual coverage value of 0.950. The actual coverage values for n equals 100, 200, 300, 400, and 500 are 0.938, 0.944, 0.9465, 0.947, and 0.948, respectively, approaching the dashed horizontal line. All data are estimated.
Model Assessment
Now that techniques for point and interval estimates for the parameters in the AR(2) model have been established, we are interested in assessing the adequacy of the AR(2) time series model. This will involve an analysis of the residuals. Recall from Section 8.2.3 that the residuals are defined by
or
Since [latex]\hat {X} _ {t}[/latex] is the one-step-ahead forecast from the time origin [latex]t - 1[/latex], this is more clearly written as
From Theorem 9.13, the shifted AR(2) model is
or
Taking the conditional expected value of both sides of this equation gives
Replacing the parameters by their point estimators, the one-step-ahead forecast from the time origin [latex]t - 1[/latex] is
Therefore, for the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] and the fitted AR(2) model with parameter estimates [latex]\hat \mu[/latex], [latex]\hat \phi_1[/latex], and [latex]\hat \phi_2[/latex], the residual at time t is
for [latex]t = 3, \, 4, \, \ldots, \, n[/latex]. The next example shows the steps associated with assessing the adequacy of the AR(2) model for the Lake Huron lake level time series.
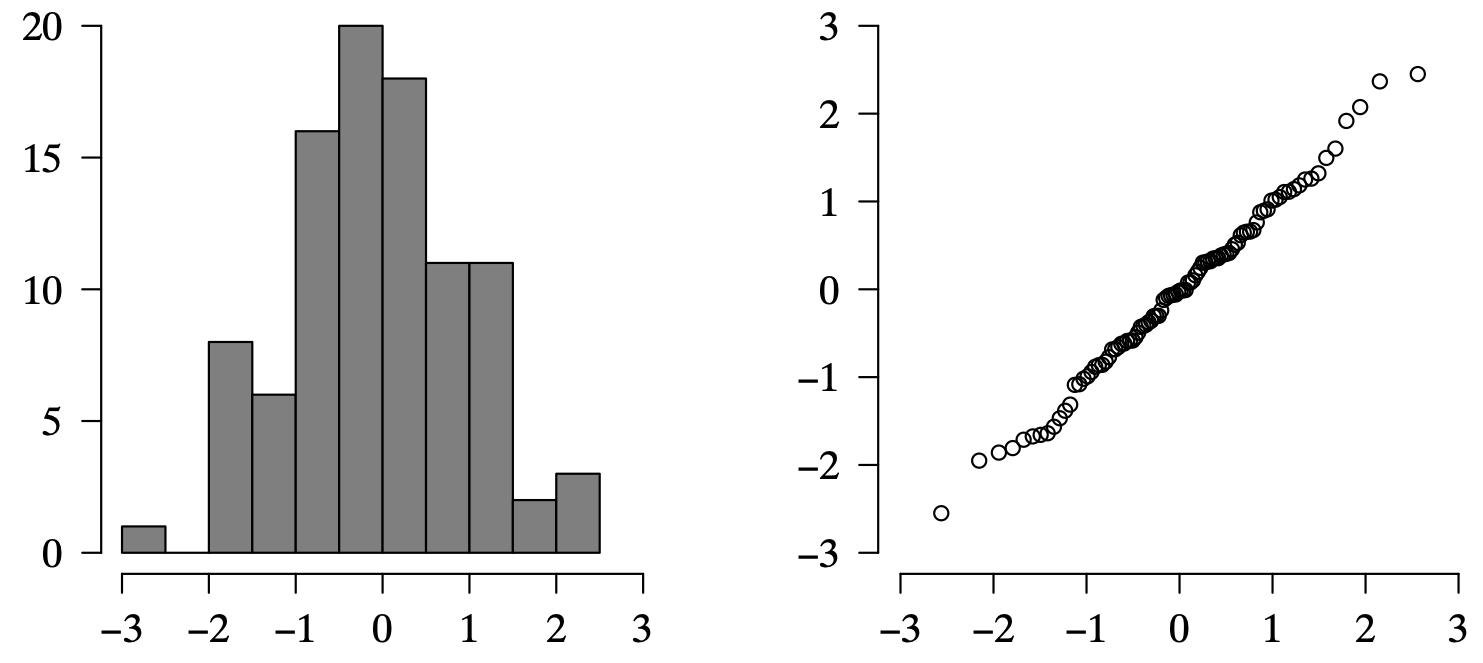
Long Description for Figure 9.24
In the histogram, the horizontal axis ranges from negative 3 to 3 in increments of 1 unit. The vertical axis ranges from 0 to 20 in increments of 5 units. The distribution of the histogram is a bell curve. There are 12 bars between negative 3 and 3, and the frequencies are 2, 0, 8, 6, 16, 20, 18, 11, 11, 2, and 3, respectively. In the Q Q plot, the horizontal and the vertical axes range from negative 3 to 3 in increments of 1 unit. Ninety six residuals are plotted in an increasing linear trend throughout the graph. The cluster is formed between negative 1 and 2 on the horizontal axis and between negative 1 and 1 on the vertical axis. The first few and the last few data points are separated from the cluster. All data are estimated.
Model Selection
We have seen a number of indicators that the AR(2) time series model seems to be an adequate model for the Lake Huron lake level time series, with the exception of a linear trend apparent by viewing the time series in Figure 9.18. The model has not been rejected by any of the model adequacy tests. We now overfit the tentative AR(2) time series model with ARMA(p, q) models of higher order. We have not yet surveyed the techniques for estimating the parameters in these models with additional terms, so for now we will let the arima function in R estimate their parameters and compare them via their AIC (Akaike's Information Criterion) statistics. The AIC statistic was introduced in Section 8.2.4
Forecasting
We now consider forecasting future values of a time series that is governed by a shifted AR(2) time series model. In the case of the Lake Huron time series, this corresponds to the one-step-ahead forecast for 1973, the two-steps-ahead forecast for 1974, the three-steps-ahead forecast for 1975, etc. To review forecasting notation, the observed time series values are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. The forecast is being made at time [latex]t = n[/latex]. The random future value of the time series that is h time units in the future is denoted by [latex]X_{n + h}[/latex]. The associated forecasted value is denoted by [latex]\hat{X}_{n + h}[/latex], and is the conditional expected value
We would like to find this forecasted value and an associated prediction interval for a shifted AR(2) model. As in Section 8.2.2, we assume that all parameters are known in the derivations that follow. We also assume that the parameters [latex]\phi_1[/latex] and [latex]\phi_2[/latex] correspond to a stationary shifted AR(2) time series model.
The shifted AR(2) model is
Replacing t by [latex]n + 1[/latex] and solving for [latex]X_{n + 1}[/latex], this becomes
Taking the conditional expected value of each side of this equation results in the one-step-ahead forecast
because [latex]x_{n - 1}[/latex] and xn have already been observed in the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. The forecasted value at time [latex]n + 1[/latex] is a function of the last two values in the time series. Applying this same process to the predicted value at time [latex]n + 2[/latex] results in the time series model
This time, the value of [latex]X_{n + 1}[/latex] has not been observed, so we replace it by its forecasted value when taking the conditional expected value of both sides of the equation
because xn has already been observed. Continuing in this fashion, a recursive formula for the forecasted value of [latex]X_{n + h}[/latex] is
Although we would prefer an explicit formula, the recursive formula is easy to implement for an observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. As in the case of the AR(1) model, long-term forecasts for a stationary AR(2) time series model tend to μ as the time horizon [latex]h \rightarrow \infty[/latex].
We would like to pair our point estimator [latex]\hat{X}_{n + h}[/latex] with an interval estimator, which is a prediction interval in this setting. The prediction interval gives us an indication of the precision of the forecast. In order to derive an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]X _ {n + h}[/latex], it is helpful to write the shifted AR(2) model as a shifted MA(∞) model. The coefficients θ1, θ2, … of a stationary shifted AR(2) model written as an MA(∞) model
are given in terms of [latex]\phi_1[/latex] and [latex]\phi_2[/latex] in Theorem 9.12. Consider this model at time [latex]t = n + 1[/latex]. Since the error terms [latex]Z_n, \, Z_{n - 1}, \, Z_{n - 2}, \, \ldots[/latex] are unknown but fixed because they are associated with the observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], the conditional population variance of [latex]X_{n+1}[/latex] is
because the population variance of μ is zero and [latex]Z_{n + 1}[/latex] is the only random term in the model. The error terms at time n and prior are observed even though unknown and can therefore be treated as constants. Likewise, considering the MA(∞) model at time [latex]t = n + 2[/latex], the conditional population variance of [latex]X_{n+2}[/latex] is
Similarly, the conditional population variance of [latex]X_{n+3}[/latex] is
Continuing in this fashion, the conditional population variance of [latex]X_{n+h}[/latex] is
If we assume that the white noise terms in the MA(∞) representation of the AR(2) time series model are Gaussian white noise terms, then [latex]X_{n+h}[/latex] is also normally distributed because a linear combination of mutually independent normal random variables is also normally distributed. So an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]X_{n+h}[/latex] is
In most practical problems, the parameters in this prediction interval will be estimated from data, which results in the following approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval.
This section has introduced the AR(2) time series model. The important results for an AR(2) model are listed below.
- The standard AR(2) model can be written algebraically and with the backshift operator B as
where [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B ^ 2[/latex] is the characteristic polynomial and [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex] (Definition 9.2).
- The shifted AR(2) model can be written algebraically and with the backshift operator B as (Theorem 9.13)
- The AR(2) model is always invertible; the AR(2) model is stationary when [latex]\phi_1[/latex] and [latex]\phi_2[/latex] fall in a triangular-shaped region in the [latex](\phi_1, \, \phi_2)[/latex] plane defined by the constraints [latex]\phi_1 + \phi_2 < 1[/latex], [latex]\phi_2 - \phi_1 < 1[/latex], and [latex]\phi_2 > -1[/latex] (Theorem 9.9).
- The AR(2) population autocorrelation function is a mixture of damped exponential functions, when [latex]\phi(B)[/latex] has real roots, or a damped sinusoidal function, when [latex]\phi(B)[/latex] has complex roots (Theorem 9.10).
- The AR(2) population partial autocorrelation function cuts off after lag 2 (Theorem 9.11), making its shape easier to recognize than the population autocorrelation function for the statistical counterparts associated with a realization of a time series.
- The stationary shifted AR(2) model can be written as a shifted MA(∞) model (Theorem 9.12).
- The four parameters in the shifted AR(2) model, μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex] and [latex]\sigma _ Z ^ {\, 2}[/latex], can be estimated from a realization of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] by the method of moments (Theorem 9.14), least squares (Theorem 9.15), and maximum likelihood using at least [latex]n = 60[/latex] or [latex]n = 70[/latex] observations. The point estimators for μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] are denoted by [latex]\hat \mu[/latex], [latex]\hat \phi_1[/latex], [latex]\hat \phi_2[/latex], and [latex]\hat \sigma _ Z ^ {\, 2}[/latex], and are typically paired with asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence intervals (Theorem 9.16).
- The forecasted value [latex]\hat{X} _ {n + h}[/latex] in an AR(2) model is a function of [latex]x_{n - 1}[/latex] and xn and can be calculated by a recursive formula. It approaches [latex]\hat \mu = \bar x[/latex] as the time horizon [latex]h \rightarrow \infty[/latex]. The associated prediction intervals have widths that increase as h increases and approach a limit as the time horizon [latex]h \rightarrow \infty[/latex] (Theorem 9.17).
The AR(1) time series model expresses the current value in the time series Xt as a constant times the previous value in the time series plus a random shock. The AR(2) time series model expresses the current value in the time series Xt as a linear combination of the previous two values in the time series plus a random shock. There is conceptually no difficulty extending this thinking to the AR(p) time series model in which the current value in the time series Xt is expressed as a linear combination of the previous p values in the time series plus a random shock. The AR(p) time series model is the subject of the next section.
9.1.3 The AR(p) Model
The order p autoregressive model, denoted by AR(p), is a straightforward generalization of the AR(2) model. The use of matrices in the derivations will be novel, along with the inability to easily visualize the stationary region as a function of the parameters. The AR(p) model is appropriate in instances in which the current value of the time series is a linear combination of the p previous values in the time series plus a random shock.
The [latex]p + 1[/latex] parameters that define an AR(p) model are the real-valued coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \phi_p[/latex], and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. The final coefficient, [latex]\phi_p[/latex], must be nonzero. The AR(p) model can be written more compactly in terms of the backshift operator B as
where [latex]\phi(B)[/latex] is the order p characteristic polynomial
The AR(p) model has the form of a multiple linear regression model with p independent variables and no intercept term. The current value Xt is being modeled as a linear combination of the p previous values of the time series, [latex]X_{t-1}, \, X_{t - 2}, \, \ldots , \, X_{t - p}[/latex], plus a white noise term Zt that provides a random shock to the model. The parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] control the inclination of the regression line ([latex]p =1[/latex]), plane ([latex]p = 2[/latex]), or hyperplane ([latex]p > 2[/latex]). The [latex]\sigma _ Z ^ {\, 2}[/latex] parameter reflects the magnitude of the dispersion of the time series values about the regression plane.
Stationarity
Theorem 8.3 indicates that all AR(p) models are invertible, but are stationary when all of the roots of [latex]\phi(B)[/latex] lie outside of the unit circle in the complex plane. Let [latex]B_1, \, B_2, \, \ldots , \, B_p[/latex] denote the p solutions of [latex]\phi(B) = 0[/latex]. For a stationary model, all of these roots will be real-valued or complex conjugate pairs that lie outside of the unit circle in the complex plane. Since [latex]\phi(B_1) = \phi(B_2) = \cdots = \phi(B_p) = 0[/latex], the order p characteristic polynomial [latex]\phi(B)[/latex] can also be written in factored form as
Unfortunately, except for the cases of [latex]p = 1[/latex] and [latex]p = 2[/latex], the region in the space of [latex]( \phi_1 , \, \phi_2 , \, \ldots , \, \phi_p )[/latex] corresponding to a stationary model cannot be expressed in a simple mathematical form. The following example illustrates how to determine whether an AR(4) model is stationary. This AR(4) model will be used in the next five examples.
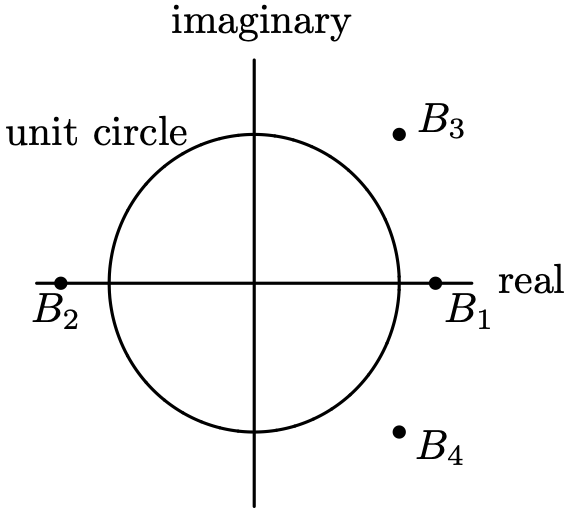
Duality
As was the case with the AR(1) and AR(2) time series models, a stationary AR(p) time series model can be written as an MA(∞) time series model. This alternative representation can be useful for estimating standard errors of forecasted values. One way to frame the problem of writing an AR(p) time series model as an MA(∞) time series model is to write the compact form of the AR(p) model as
and divide both sides by [latex]\phi(B)[/latex], which results in
Therefore, the conversion from the AR(p) form of the model to the MA(∞) form involves finding the coefficients [latex]\theta_1, \, \theta_2, \, \ldots[/latex] such that
The coefficients [latex]\theta_1, \, \theta_2, \, \ldots[/latex] essentially correspond to finding the inverse of the [latex]\phi(B)[/latex] characteristic polynomial. Taking the expected value of both sides of this equation leads to the important result: [latex]E \left[ X_t \right] = 0[/latex] for all values of t. As was the case of the AR(2) time series model, the coefficients for the MA(∞) time series model are found by equating coefficients. This process will be illustrated in the next example for the AR(4) model. Generalization to the AR(p) model is straightforward.
Population Autocorrelation Function
We now pivot to the derivation of the population autocovariance and autocorrelation functions. Assuming that the parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] are associated with a stationary model, the AR(p) model
can be multiplied by [latex]X_{t - k}[/latex] to give
Taking the expected value of both sides of this equation for [latex]k = 0[/latex] results in
and the recursive equation
for [latex]k = 1, \, 2, \, \ldots[/latex] because Zt has expected value zero and is independent of [latex]X_{t - k}[/latex]. For [latex]k = 1, \, 2, \, \ldots , \, p[/latex], the recursive equation can be written as the system of linear equations
which relies on the symmetry of the population autocovariance function: [latex]\gamma(-k) = \gamma(k)[/latex]. This linear system of p equations in [latex]p + 1[/latex] unknowns can be written in matrix form as
where
Given the values of the parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex], this set of linear equations and
one can compute the first [latex]p + 1[/latex] population autocovariances [latex]\gamma(0), \, \gamma(1), \, \ldots , \, \gamma(p)[/latex] by solving these linear equations. The recursion relationship can be used to compute subsequent autocovariances.
Dividing both sides of the recursive equation for calculating population autocovariance by [latex]\gamma(0) = V \left[ X_t \right][/latex] gives the recursive equation
for [latex]k = 1, \, 2, \, \ldots[/latex]. Exploiting the symmetry of the [latex]\rho(k)[/latex] function, the first p of these equations are
Since [latex]\rho(0) = 1[/latex], this linear system of p equations in the p unknowns [latex]\rho(1), \, \rho(2), \, \ldots , \, \rho(p)[/latex] can be written in matrix form as
where
Given the values of the parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], these linear equations can be solved for the initial p population autocorrelation function values [latex]\rho(1), \, \rho(2), \, \ldots , \, \rho(p)[/latex], and the recursive function can be used to calculate subsequent values of the population autocorrelation values.
As was the case with the AR(2) time series model, (a) the real roots of [latex]\phi(B)[/latex] correspond to contributions to the population autocorrelation function which are mixtures of damped exponential terms, and (b) the complex conjugate roots of [latex]\phi(B)[/latex] correspond to contributions to the population autocorrelation function which are damped sinusoidal terms.
These equations bear some practical use in that the first psample autocorrelation function values, [latex]r_1, \, r_2, \, \ldots , \, r_p[/latex], can be calculated from an observed time series and used as approximations for [latex]\rho(1), \, \rho(2), \, \ldots , \, \rho(p)[/latex], yielding estimators for [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex]. These estimates are known as the Yule–Walker estimators. These can in turn be used as initial estimates for finding point estimates for [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] by, for example, least squares or maximum likelihood estimation, should numerical methods be required.
The results concerning the calculation of the population autocovariance function [latex]\gamma(k)[/latex] and the population autocorrelation function [latex]\rho(k)[/latex] are summarized below.
The system of linear equations in Theorem 9.18, whether written in terms of [latex]\gamma(k)[/latex] or [latex]\rho(k)[/latex] as [latex]\gamma = \Gamma \phi[/latex] or [latex]\rho = P \phi[/latex], is known in time series analysis as the Yule–Walker equations.
Population Partial Autocorrelation Function
We now determine the population partial autocorrelation function for an AR(p) model. Using Definition 7.4, the initial population partial autocorrelation values are
etc. One distinctive characteristic of the AR(p) population partial autocorrelation function is that it cuts off after lag p. To see why this is the case, consider the first p columns of the matrix in the numerator of [latex]\rho ^ * (k)[/latex] for [latex]k > p[/latex]:
Using Theorem 9.18, the last column of the matrix in the numerator of [latex]\rho ^ * (k)[/latex] is
The last column of the matrix in the numerator of [latex]\rho ^ * (k)[/latex] is a linear combination of the first p columns with coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex]. Thus, the matrix in the numerator of the calculation of [latex]\rho ^ * (k)[/latex] is singular, which means that its determinant is zero. So [latex]\rho ^ * (k) = 0[/latex] for [latex]k = p + 1, \, p + 2, \, \ldots[/latex] for an AR(p) time series model. This constitutes a proof of the following result.
A graph of the sample partial autocorrelation function [latex]r^*_k[/latex] for the first few values of k, should also cut off after lag p if the AR(p) model is appropriate. This sample partial autocorrelation function shape is easier to recognize than the associated sample autocorrelation function shape because cutting off is typically easier to recognize than tailing off in the presence of random sampling variability.
There is a second interpretation of the partial autocorrelation function that ties it more closely to determining the order of the autoregressive portion of the model. The partial autocorrelation at lag k is the value of the final coefficient [latex]\phi_k[/latex] in an autoregressive model of order k. This coefficient measures the excess correlation at lag k which is not accounted for by an autoregressive model of order [latex]k - 1[/latex]. It is for this reason that many authors use the notation [latex]\phi_{kk}[/latex] for the population lag k partial autocorrelation.
The population autocorrelation function and the population partial autocorrelation functions can be calculated using the formulas given here, but can also be calculated using the R ARMAacf function, as illustrated in the next example.
|
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|---|---|---|---|---|---|---|---|
|
[latex]\rho(k)[/latex] |
0.8409 |
0.6420 |
0.3935 |
0.2617 |
0.1776 |
0.1659 |
0.1506 |
|
[latex]\rho^*(k)[/latex] |
0.8409 |
−0.2222 |
−0.2857 |
0.3000 |
0 |
0 |
0 |
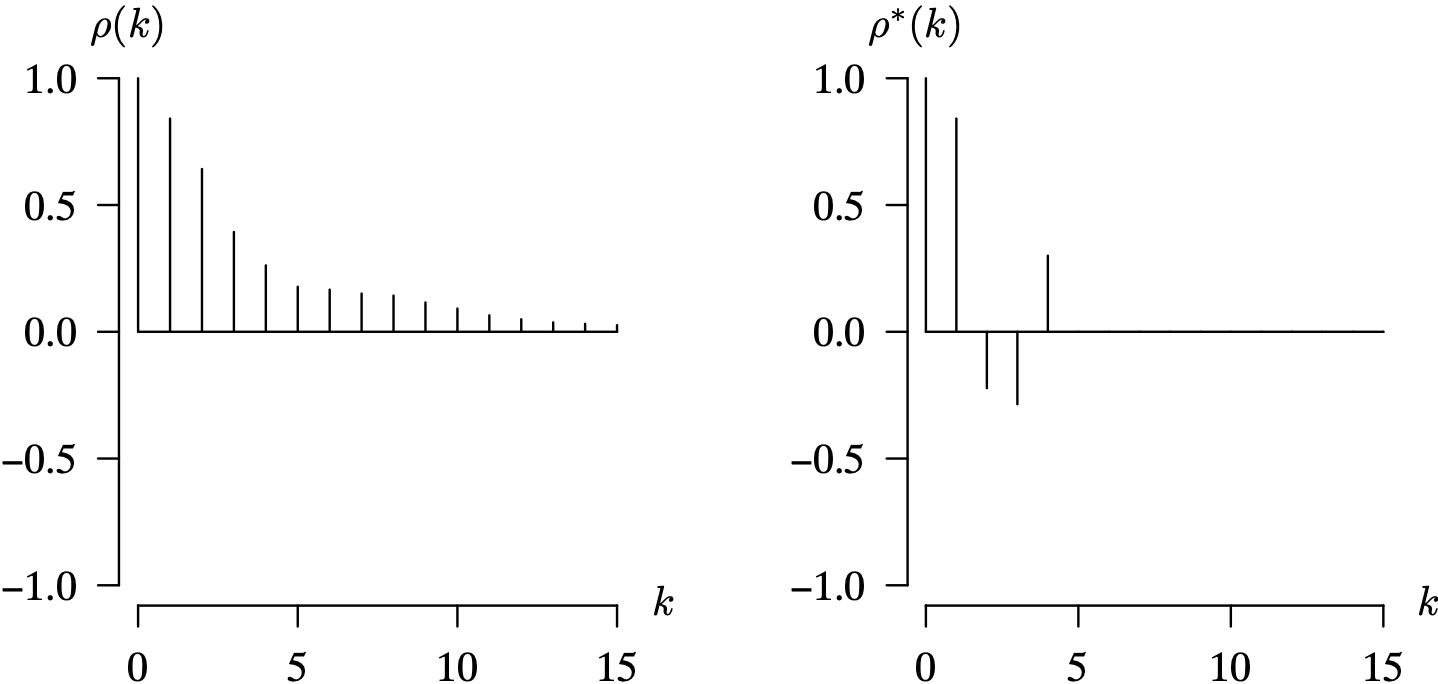
Long Description for Figure 9.27
In the first correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis rho of k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at rho subscript k value 0.0. The values of rho of k decrease exponentially from 1.0 to 0.02. In the second correlogram, the horizontal axis k ranges from 0 to 15 and the vertical axis rho star k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The function rho star of k behaves like a damped sinusoidal pattern and the values are 1.0, 0.8, negative 0.2, negative 0.25, and 0.25 for k values 0, 1, 2, 3, and 4. All data are estimated.
The Shifted AR(p) Model
The standard AR(p) model from Definition 9.3 is not of much practical use because most real-world time series are not centered around zero. Adding a shift parameter μ overcomes this shortcoming. Since population variance and covariance are unaffected by a shift, the associated population autocorrelation and partial autocorrelation functions remain the same as those given in Theorems 9.18 and 9.19.
The shifted AR(p) model can be written in terms of the backshift operator B as
where [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B^2 - \cdots - \phi_p B ^ p[/latex]. The practical problem of fitting a shifted AR(p) model to an observed time series of n values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] will be illustrated later in this subsection.
Simulation
An AR(p) time series can be simulated by appealing to the defining formula for the AR(p) model. Iteratively applying the defining formula for a standard AR(p) model
from Definition 9.3 results in the simulated values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. The difficult aspect of devising a simulation algorithm is generating the first p simulated values, [latex]X_1, \, X_2, \, \ldots, \, X_p[/latex]. For simplicity, assume that the white noise terms are Gaussian white noise terms. There are two approaches to overcome this initialization problem. The first approach generates [latex]X_1, \, X_2, \, \ldots , \, X_p[/latex] from a multivariate normal distribution with population mean p-vector [latex]\boldsymbol{0} = (0, \, 0, \, \ldots , \, 0) ^ \prime[/latex] and [latex]p \times p[/latex] variance–covariance matrix
which was defined in Theorem 9.18. The algorithm given below generates initial time series observations [latex]X_1, \, X_2, \, \ldots , \, X_p[/latex] as indicated above, and then uses an additional [latex]n - p[/latex] Gaussian white noise terms [latex]Z_{p + 1}, \, Z_{p + 2}, \, \ldots, \, Z_n[/latex] to generate the remaining time series values [latex]X_{p + 1}, \, X_{p + 2}, \, \ldots, \, X_n[/latex] using the AR(p) defining formula from Definition 9.3. Indentation denotes nesting in the algorithm.
The [latex](p + 2)[/latex]-parameter shifted AR(p) time series model which includes a population mean parameter μ can be simulated by simply adding μ to each time series observation generated by this algorithm. The next example implements this algorithm in R.
Using the plot.ts function to make a plot of the time series contained in x, the acf function to plot the associated correlogram, the pacf function to plot the associated sample partial autocorrelation function, and the layout function to arrange the graphs as in Example 7.24, the resulting trio of graphs are displayed in Figure 9.28. The sample partial autocorrelation function has four statistically significant spikes at lags 1, 2, 3, and 4 which is consistent with an AR(4) model. The spikes cut off after lag 4 as expected from the population counterparts in Figure 9.27. The approximate 95% confidence intervals indicated by the dashed lines show that the values of the sample partial autocorrelation function do not significantly differ from zero at lags beyond lag 4. The sample autocorrelation function displays a mixture of damped exponential terms damped sinusoidal terms as expected, with statistically significant autocorrelations at the first two lags: [latex]r ^ * _ 1 = 0.7351[/latex] and [latex]r ^ * _ 2 = 0.4417[/latex]. The time series plot shows that observations tend to linger on one side of the population mean (indicated by a horizontal line at [latex]\mu = 0[/latex]), which is consistent with the two initial statistically significant positive spikes in the sample autocorrelation function.
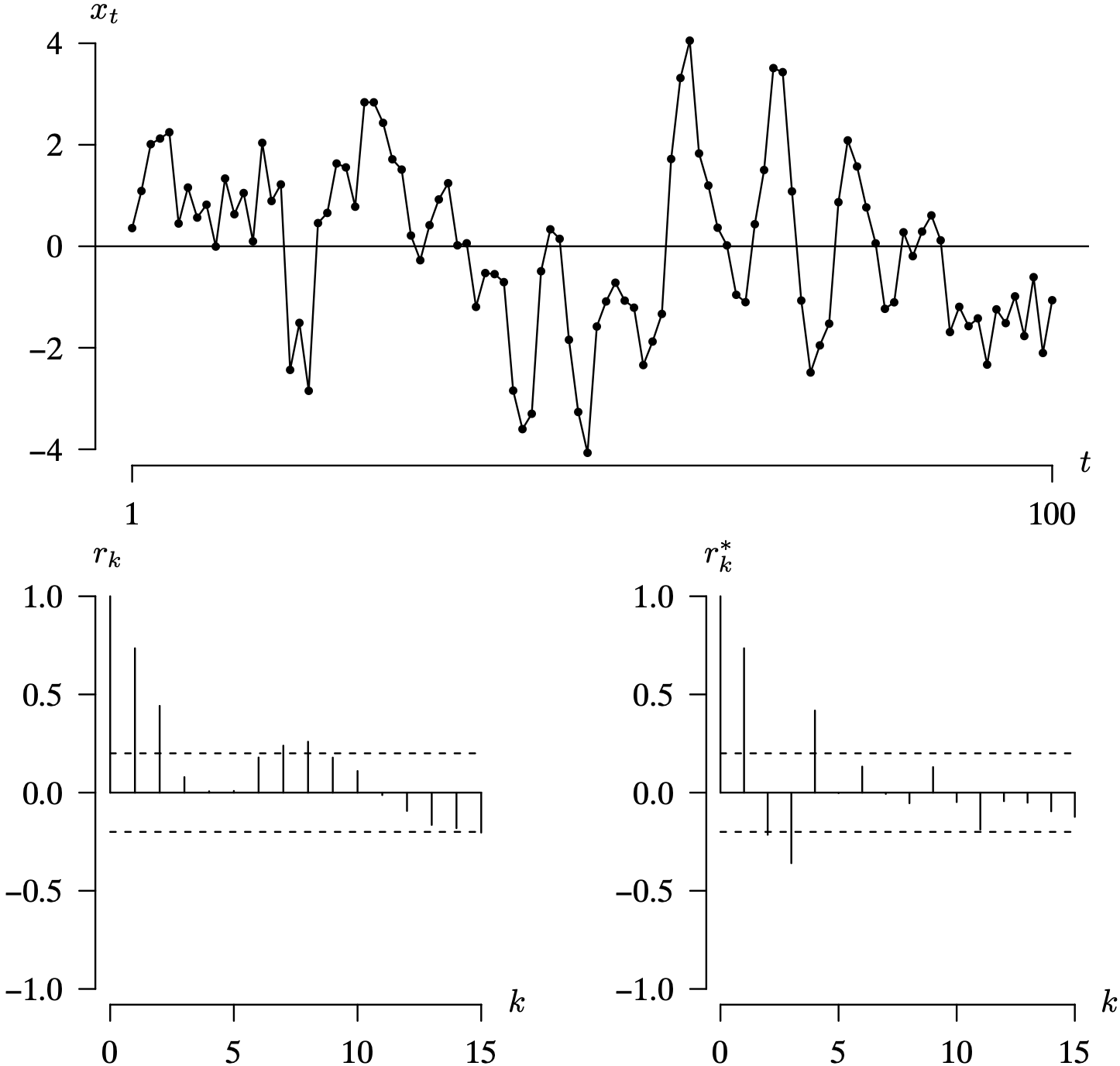
Long Description for Figure 9.28
In the time series plot, the horizontal axis t ranges from 1 to 100. The vertical axis x subscript t ranges from negative 4 to 4 in increments of 2 units. A horizontal line is drawn at 0. The first 17 values are positive and range between 0 and 2, the next 3 values are negative and range between negative 1 and negative 3. The values then increase to 3 at t equals 27 and decrease to the lowest point negative 4 at t equals negative 53 with many fluctuations. The values then increase to a peak of 4 at t equals 64, and then have a pattern of successive, decreasing peaks for the remaining t values. In the first correlogram, the horizontal axis k ranges from 0 to 15 and the vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The first 6 r subscript k values decrease progressively from 1.0 to 0. For k values 6 to 10, the r subscript k values follow a bell shape, reaching a peak of 0.25, and the last 5 values decrease from negative 0.01 to negative 0.2. In the second correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r star subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The r star subscript k values alternate signs, approximately following a damped sinusoidal pattern with decreasing magnitude. All data are estimated.
We recommend running the simulation code from the previous example several dozen times in a loop and viewing the associated plots of xt, rk, and [latex]r_k^*[/latex] in search of patterns. This will allow you to see how various realizations of this simulated AR(4) time series model vary from one realization to the next. So when you then view a single realization of a real-life time series, you will have a sense of how far these plots might deviate from their expected patterns.
There is a second way to overcome the initialization problem in simulating observations from an AR(p) time series. This second technique starts the time series with p initial arbitrary values, and then allows the time series to “warm up” or “burn in” for several time periods before producing the first observation X1. Reasonable p initial arbitrary values for the standard AR(p) model are 0; reasonable p initial arbitrary values for the shifted AR(p) model are μ. This approach can be implemented in R with the filter function with "recursive" as the method argument. The code below generates [latex]n = 100[/latex] values in the AR(4) time series model from the previous example using a warm-up period of 50 observations.

This is also the approach taken by the built-in R function named arima.sim, which simulates a realization of a time series. Using the arima.sim function means that [latex]n = 100[/latex] observations from the AR(4) time series model from the previous example can be simulated using a single command, using a warm-up period of 50 observations.
The remaining topics associated with the AR(p) time series model are statistical in nature: parameter estimation, model assessment, model selection, and forecasting. We begin with parameter estimation.
Parameter Estimation
The [latex]p + 2[/latex] parameters to estimate in a shifted AR(p) time series model are [latex]\phi_1, \, \phi_2 , \, \ldots , \, \phi_p, \, \mu , \, \sigma _ Z ^ {\, 2}[/latex]. There are three techniques for estimating these parameters considered here: method of moments, least squares, and maximum likelihood estimation. These techniques were introduced in Section 8.2.1. These three techniques are outlined in the following paragraphs.
Approach 1: Method of moments. In the case of estimating the [latex]p + 2[/latex] parameters in the shifted AR(p) time series model by the method of moments, we match the population and sample first-order moments, second-order moments, lag 1 autocorrelation, lag 2 autocorrelation, [latex]\ldots[/latex], lag p autocorrelation. Placing the population moments on the left-hand side of the equation and the associated sample moments on the right-hand side of the equation results in [latex](p + 2)[/latex] equations in [latex](p + 2)[/latex] unknowns:
Since [latex]E \left[ X_t \right] = \mu[/latex] for a stationary shifted AR(p) time series model, the first equation gives the method of moments estimator [latex]\hat \mu = \bar X[/latex]. Recall from Theorem 9.18 that the relationship between [latex]\phi_1, \, \phi_2 , \, \ldots , \, \phi_p[/latex] and [latex]\rho(1), \, \rho(2) , \, \ldots , \, \rho(p)[/latex] is given by the matrix equation
where
Satisfying the method of moments criteria, the lag k population autocorrelation [latex]\rho(k)[/latex] can be replaced with its statistical analog rk, for [latex]k = 1, \, 2, \, \ldots, \, p[/latex]. The resulting matrix equation is
where
This matrix equation can be solved for the method of moments estimators as
These are known as the Yule–Walker estimators because of their relationship to the Yule–Walker equations. Finally, the remaining parameter to estimate is the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. From Theorem 9.18,
Multiplying and dividing the right-hand side of this equation by [latex]\gamma(0)[/latex] gives
Replacing these elements by their method of moments estimators gives
which can be expressed in matrix form as
Since the formula for these estimators does not require any iterative methods, the method of moments estimators are often used as initial parameter estimates for the least squares estimators and the maximum likelihood estimators, which do require iterative methods. These point estimators for the parameters in a shifted AR(p) model are summarized below.
Approach 2: Least squares. Consider the shifted stationary AR(p) model
For least squares estimation, we first establish the sum of squares S as a function of the parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex]. We leave the optimization to the R ar function in order to calculate the least squares estimators of μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex]. Once these least squares estimators have been determined, the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex] will be estimated.
The sum of squared errors is
If this derivation were being done by hand, we would now calculate the partial derivatives of S with respect to the unknown parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex], equate them to zero and solve. As was the case with the AR(1) and AR(2) models, there is no closed-form solution, so numerical methods are required to calculate the parameter estimates. In the example that follows, we will use the ar function in R to determine the least squares parameter estimates that minimize S.
The last parameter to estimate is the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. The same estimator as the method of moments will be used:
Least squares estimation for a shifted AR(p) time series model is summarized below.
We now use numerical methods to find the least squares estimates for the unknown parameters in the AR(p) time series model for the Lake Huron time series from Example 9.14.
|
p |
[latex]\hat \mu[/latex] |
[latex]\hat \phi_1[/latex] |
[latex]\hat \phi_2[/latex] |
[latex]\hat \phi_3[/latex] |
[latex]\hat \phi_4[/latex] |
[latex]\hat \sigma _ Z ^ {\, 2}[/latex] |
S |
|---|---|---|---|---|---|---|---|
|
1 |
579.00 |
0.8364 |
0.5090 |
49.38 |
|||
|
2 |
579.00 |
1.0217 |
−0.2376 |
0.4540 |
43.64 |
||
|
3 |
579.00 |
1.0719 |
−0.3653 |
0.1088 |
0.4488 |
42.66 |
|
|
4 |
579.00 |
1.0738 |
−0.3739 |
0.0569 |
0.0625 |
0.4475 |
42.12 |
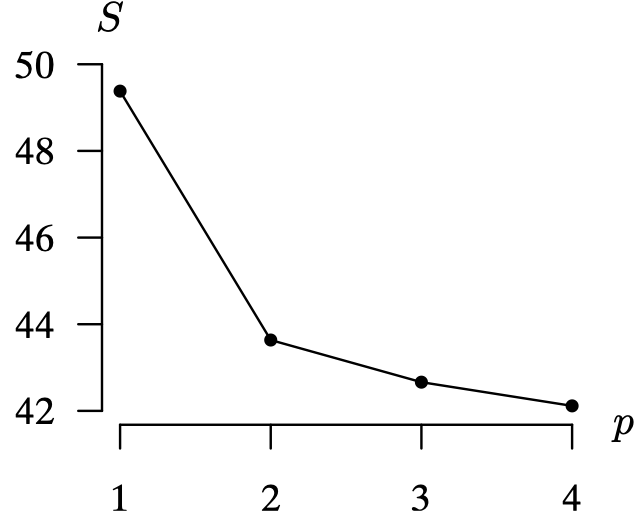
Approach 3: Maximum likelihood estimation. The procedure for determining the maximum likelihood estimators for the unknown parameters in a shifted AR(p) time series model follows along the same lines as in the AR(1) and AR(2) time series models from the previous subsections. Once again, to use maximum likelihood estimation, we must assume that the random shocks from the white noise are Gaussian white noise, with associated probability density function
for [latex]t = 1, \, 2, \, \ldots, \, n[/latex]. Determining the likelihood function, which is the joint probability density function of the observed values in the time series [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex], involves finding
where the [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] arguments on L and the μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex], and [latex]\sigma _Z ^ {\, 2}[/latex] arguments on f have been dropped for brevity and [latex]n > p[/latex]. As before, it is not possible to simply multiply the marginal probability density functions because the values in the AR(p) time series model are correlated. As in the case of the AR(1) and AR(2) models, we use the transformation technique to find the conditional joint probability density function of [latex]X_{p + 1}, \, X_{p + 2}, \, \ldots, \, X_n[/latex] conditioned on [latex]X_1 = x_1[/latex], [latex]X_2 = x_2[/latex], [latex]\ldots[/latex], [latex]X_p = x_p[/latex], which is denoted by
for [latex]\left( x_{p + 1}, \, x_{p + 2}, \, \ldots, \, x_n \right) \in {\cal R} ^ {n - p}[/latex]. This conditional joint probability density function is multiplied by the marginal joint probability density function of X1, X2, [latex]\ldots[/latex], Xp (which has the p-dimensional multivariate normal distribution) resulting in a joint probability density function of [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]:
for [latex]\left( x_1, \, x_2, \, \ldots, \, x_n \right) \in {\cal R} ^ n[/latex]. This function serves as the likelihood function, which should be maximized with respect to the unknown parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\ldots[/latex], [latex]\phi_p[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex]. We leave the maximization to the ar and arima functions in R when determining the maximum likelihood estimates for the parameters for a particular time series to be fitted to the shifted AR(p) time series model.
In addition to point estimators for the parameters, we are also interested in confidence intervals that capture the precision of the point estimators. The population variance of the vector of parameter estimators [latex]\hat \phi = ( \hat \phi_1 , \, \hat \phi_2 , \, \ldots , \, \hat \phi_p ) ^ \prime[/latex] is given by the variance–covariance matrix
Since the maximum likelihood estimators for [latex]\phi_1, \, \phi_2 , \, \ldots , \, \phi_p[/latex] are asymptotically unbiased and normally distributed under certain regularity conditions,
For [latex]p = 1[/latex], this reduces to
For [latex]p = 2[/latex], this reduces to
These asymptotic results for [latex]p = 1[/latex] and [latex]p = 2[/latex] were used in the confidence intervals given in Theorems 9.7 and 9.16. When the quantities in this expression are replaced by their statistical counterparts, the estimated variance–covariance matrix of the vector [latex]\hat \phi[/latex] is
Using the diagonal elements of this matrix and the asymptotic normality of maximum likelihood estimators, an asymptotically exact [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]\phi_i[/latex] is easily constructed.
The maximum likelihood estimates and associated confidence intervals will be illustrated for an economic time series in the next example.
Model Assessment
Now that techniques for point and interval estimates for the parameters in the AR(p) model have been established, we are interested in assessing the adequacy of the fitted AR(p) time series model. This will involve an analysis of the residuals. Recall from Section 8.2.3 that the residuals are defined by
or
Since [latex]\hat{X} _ {t}[/latex] is the one-step-ahead forecast from the time origin [latex]t - 1[/latex], this is more clearly written as
From Theorem 9.20, the shifted AR(p) model is
or
Taking the conditional expected value of both sides of this equation gives
Replacing the parameters by their point estimators, the one-step-ahead forecast from the time origin [latex]t - 1[/latex] is
Therefore, for the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] and the fitted AR(p) model with parameter estimates [latex]\hat \mu[/latex], [latex]\hat \phi_1[/latex], [latex]\hat \phi_2[/latex], [latex]\ldots[/latex], [latex]\hat \phi_p[/latex], the residual at time t is
for [latex]t = p + 1, \, p + 2, \, \ldots, \, n[/latex]. The next example shows the steps associated with assessing the adequacy of the AR(4) model for the time series of annual lynx pelt sales.
Forecasting
We now consider the question of forecasting future values of a time series that is governed by a shifted AR(p) time series model. In the case of the annual lynx pelt sales time series, this corresponds to the one-step-ahead forecast for 1912, the two-steps-ahead forecast for 1913, the three-steps-ahead forecast for 1914, etc. To review forecasting notation, the observed time series values are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. The forecast is being made at time [latex]t = n[/latex]. The random future value of the time series that is h time units in the future is denoted by [latex]X_{n + h}[/latex]. The associated forecasted value is denoted by [latex]\hat{X}_{n + h}[/latex], and is the conditional expected value
We would like to find this forecasted value and an associated prediction interval for a shifted AR(p) model. As in Section 8.2.2, we assume that all parameters are known in the derivations that follow. We also assume that the parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] correspond to a stationary shifted AR(p) time series model and [latex]p < n[/latex].
The shifted AR(p) model is
Replacing t by [latex]n + 1[/latex] and solving for [latex]X_{n + 1}[/latex], this becomes
Taking the conditional expected value of each side of this equation results in the one-step-ahead forecast
because the final p observations [latex]x_{n - p + 1}, \, x_{n - p + 2}, \, \ldots , \, x_n[/latex] in the time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] have already been observed. The forecasted value at time [latex]n + 1[/latex] is a function of the final p values in the time series. Applying this same process to the predicted value at time [latex]n + 2[/latex] results in the time series model
This time, the value of [latex]X_{n + 1}[/latex] has not been observed, so we replace it by its forecasted value when taking the conditional expected value of both sides of the equation
because [latex]x_{n - p + 2}, \, x_{n - p + 3}, \, \ldots , \, x_n[/latex] have already been observed. Continuing in this fashion, a recursive formula for the forecasted value of [latex]X_{n + h}[/latex] is
Although we would prefer an explicit formula, the recursive formula is easy to implement for an observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. As in the case of the AR(1) and AR(2) models, long-term forecasts for a stationary AR(p) time series model tend to μ as the time horizon [latex]h \rightarrow \infty[/latex].
We would like to pair the point estimator [latex]\hat{X}_{n + h}[/latex] with an interval estimator, which is a prediction interval in this setting. The prediction interval gives us an indication of the precision of the forecast. In order to derive an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]X _ {n + h}[/latex], it is helpful to write the shifted AR(p) model as a shifted MA(∞) model. The coefficients θ1, θ2, … of a stationary shifted AR(p) model written as an MA(∞) model
are given in terms of [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] as was illustrated for [latex]p = 4[/latex] in Example 9.23. Consider this model at time [latex]t = n + 1[/latex]. Since the error terms [latex]Z_n, \, Z_{n - 1}, \, Z_{n - 2}, \, \ldots[/latex] are unknown but fixed because they are associated with the observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], the conditional population variance of [latex]X_{n + 1}[/latex] is
because the population variance of μ is zero and [latex]Z_{n + 1}[/latex] is the only random term in the model. The error terms at time n and prior are observed and can therefore be treated as constants. Likewise, considering the MA(∞) model at time [latex]t = n + 2[/latex], the conditional population variance of [latex]X_{n+2}[/latex] is
Similarly, the conditional population variance of [latex]X_{n+3}[/latex] is
Continuing in this fashion, the conditional population variance of [latex]X_{n+h}[/latex] is
If we assume that the white noise terms in the MA(∞) representation of the AR(p) time series model are Gaussian white noise terms, then [latex]X_{n + h}[/latex] is also normally distributed because a linear combination of mutually independent normal random variables is also normally distributed. So an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]\hat{X} _ {n + h}[/latex] is
In most practical problems, the parameters in this prediction interval will be estimated from data, which results in the following approximate two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval provided next.
This subsection has introduced the AR(p) time series model. The important results for an AR(p) model are listed below.
- The standard AR(p) model can be written algebraically and with the backshift operator B as
where [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B ^ 2 - \cdots - \phi_p B ^ p[/latex] is the characteristic polynomial and [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex] (Definition 9.3).
- The shifted AR(p) model can be written algebraically and with the backshift operator B as (Theorem 9.20)
- The AR(p) model is always invertible; the AR(p) model is stationary when the solutions of [latex]\phi(B) = 0[/latex] all lie outside of the unit circle in the complex plane (Theorem 8.3).
- The AR(p) population autocorrelation function is a mixture of damped exponential functions, associated with real roots of [latex]\phi(B) = 0[/latex], and damped sinusoidal functions, associated with complex roots of [latex]\phi(B) = 0[/latex] (Theorem 9.18).
- The AR(p) population partial autocorrelation function cuts off after lag p (Theorem 9.19), making its shape easier to recognize than the population autocorrelation function for the statistical counterparts associated with a realization of a time series.
- The stationary shifted AR(p) model can be written as a shifted MA(∞) model (as illustrated in Example 9.23).
- The [latex]p + 2[/latex] parameters in the shifted AR(p) model, μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\dots[/latex], [latex]\phi_p[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex], can be estimated from a realization of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] by the method of moments (Theorem 9.21), least squares (Theorem 9.22), and maximum likelihood. The point estimators for μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], [latex]\dots[/latex], [latex]\phi_p[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex] are denoted by [latex]\hat \mu[/latex], [latex]\hat \phi_1[/latex], [latex]\hat \phi_2[/latex], [latex]\ldots[/latex], [latex]\hat \phi_p[/latex], and [latex]\hat \sigma _ Z ^ {\, 2}[/latex], and are typically paired with asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence intervals (Theorem 9.23).
- The forecasted value [latex]\hat{X} _ {n + h}[/latex] in a shifted AR(p) model is a function of the last p values in an observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] and can be calculated by a recursive formula. The forecast approaches [latex]\hat \mu = \bar x[/latex] as the time horizon [latex]h \rightarrow \infty[/latex]. The associated prediction interval has width that increases as h increases and approaches a limit as the time horizon [latex]h \rightarrow \infty[/latex] (Theorem 9.24).
9.1.4 Computing
The R time series functions used in this section are summarized here. The ARMAacf function computes the population autocorrelation function or the population partial autocorrelation function for an ARMA(p, q) time series model. The generic version of the function is
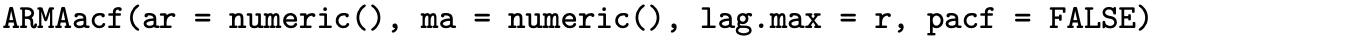
where ar is a vector containing the autoregressive coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], ma is a vector containing the moving average coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], lag.max contains the number of lags required, and pacf is a logical object. The function returns [latex]\rho(0), \, \rho(1), \, \ldots , \, \rho( {\tt lag.max} )[/latex] when pacf is FALSE, or [latex]\rho ^ * (1), \, \rho ^ * (2), \, \ldots , \, \rho ^ * ( {\tt lag.max} )[/latex] when pacf is TRUE. The ARMAacf function is illustrated in Example 9.25.
The arima.sim function generates a simulation of a time series. The generic version of the function is

where model is a list with components ar containing the autoregressive coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], and ma containing the moving average coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], n is the length of the simulated time series to be generated, rand.gen is a function to generate the white noise terms, n.start is the length of the warm-up period, and start.innov is a time series of white noise terms used in the warm-up period. The returned value is a vector containing the n simulated time series values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. The arima.sim function is illustrated in Examples 9.2, 9.13, and 9.18. The warm-up period associated with the arima.sim function can be avoided by generating initial values from the appropriate multivariate distribution. For an AR(1) model with Gaussian white noise error terms, the rnorm function, whose generic syntax is

where n is the number of random variates to generate, mean is the population mean, and sd is the population standard deviation, can be used to seed the simulated time series. The rnorm function is illustrated in Example 9.1. For an AR(p) model, with [latex]p > 1[/latex], with Gaussian white noise error terms, the mvrnorm function from the MASS package, whose generic syntax is
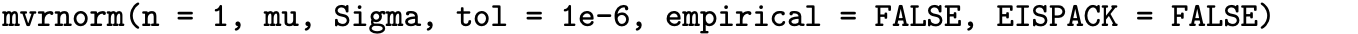
where n is the number of random vectors to generate, mu is the population mean vector, and Sigma is the population variance–covariance matrix, can be used to seed the simulated time series. The mvrnorm function is illustrated in Examples 9.12 and 9.26.
When determining parameter estimates that cannot be expressed in closed form, the optim function provides general-purpose optimization capability that can be applied to minimizing the sum of squares to find the least squares estimates or maximizing the log likelihood function to find the maximum likelihood estimators. The generic syntax for optim is

where par is a vector containing initial parameter estimates and fn is the function to be minimized (by default). The optim function is illustrated in Examples 9.5, 9.6, and 9.16. A parameter estimation function that is exclusively for autoregressive time series models is ar. The generic format for ar is
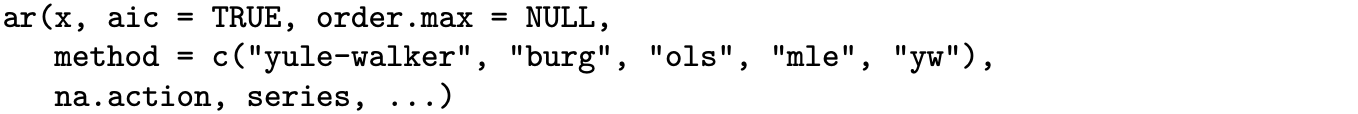
where x is a vector containing the observed time series values, aic is a logical variable (TRUE means that the Akaike Information Criterion is used to choose the order of the model and FALSE means that an autoregressive model of order order.max is fitted), order.max is maximum order of the autoregressive model to fit, method is the estimation method ("yule-walker" or "yw" for Yule–Walker, "burg" for Burg's algorithm, "ols" for least squares, "mle" for maximum likelihood), and na.action indicates how to handle missing values in the time series. The ar function is illustrated in Examples 9.7, 9.8, 9.10, 9.17, 9.19, 9.21, 9.27, 9.28, and 9.31. The arima function also estimates parameters from an observed time series. The generic format for arima is

where x is a vector containing the observed time series values, order is a vector containing the values of p, d, and q, include.mean is a logical variable (TRUE includes estimation of a population mean term μ and FALSE estimates just the parameters in the standard model), and method is CSS (conditional sum of squares) or ML (maximum likelihood). The arima function is illustrated in Examples 9.9, 9.18, 9.20, and 9.29.
Three functions were introduced in this section for assessing model adequacy. The Box.test function computes the Box–Pierce or Ljung–Box test statistic and associated p-value. The generic syntax is
where x is a vector containing the observed time series values, lag is the number of sample autocorrelation function values to be used in the test, type is either "Box-Pierce" or "Ljung-Box", and fitdf is the number of degrees of freedom to be subtracted in the case of x being a time series of residuals. The Box.test function is illustrated in Examples 9.8, 9.19, and 9.30, along with the hist and qqnorm functions, which are helpful in visually assessing the normality of the residuals.
Forecasting can be performed automatically using the generic predict function, which calculates predicted values of a time series from a fitted function. The predict function is illustrated in Examples 9.10, 9.21, and 9.31.
More details on the R functions used in this section can be found using the help function. Sample invocations of the functions are displayed using the example function.
This concludes the introduction to the autoregressive time series model, with subsections devoted to the AR(1), AR(2), and AR(p) models. An analogous treatment of moving average models is contained in the next section.
9.2 Moving Average Models
Moving average models for a time series will be introduced in this section. A moving average model of order q is a special case of an ARMA(p, q) model with no autoregressive terms (that is, [latex]p = 0[/latex]) and q moving average terms, specified as
where [latex]\theta_1, \, \theta_2 , \ldots , \, \theta_q[/latex] are real-valued parameters and [latex]\left\{ Z_t \right\}[/latex] is a time series of white noise. Rather than diving right into an MA(q) model, we first have separate subsections for the MA(1) and MA(2) models because the mathematics are somewhat easier than the general case and some important geometry and intuition can be developed with these restricted models. In the subsection on the MA(1) model that follows, we will
- define the time series model for [latex]\left\{ X_t \right\}[/latex],
- determine the values of the parameters associated with an invertible model,
- derive the population autocorrelation and partial autocorrelation functions,
- develop algorithms for simulating observations from the time series,
- inspect simulated realizations to establish patterns, and
- estimate parameters from a time series realization [latex]\left\{ x_t \right\}[/latex].
The important steps of model assessment, model selection, and forecasting future values of the times series are left as exercises because they follow along the same lines as those steps for the autoregressive models covered in the previous section.
The purpose of deriving the population autocorrelation and partial autocorrelation functions is to build an inventory of shapes and patterns for these functions that can be used to identify tentative time series models from their sample counterparts by making a visual comparison between population and sample versions. This inventory of shapes and patterns plays an analogous role to knowing the shapes of various probability density functions (for example, the bell-shaped normal probability density function or the rectangular-shaped uniform distribution) in the analysis of univariate data in which the shape of the histogram is visually compared to the inventory of probability density function shapes.
In the MA(1) subsection that follows, a single example of a time series will be carried through the various statistical procedures given in the list above. Stationarity plays a critical role in time series analysis because we are not able to forecast future values of the time series without knowing that the probability model is stable over time. This is why the visual assessment of a plot of the time series is always a critical first step in the analysis of a time series. Fortunately, all MA(q) time series models are stationary.
9.2.1 The MA(1) Model
The moving average model with one term is the simplest of the ARMA family of time series models in terms of the ability to derive probabilistic properties.
An observed value in the time series, Xt, is given by the current white noise term, plus the parameter θ multiplied by the white noise term from one time period ago. No subscript is necessary on the θ parameter because there is only one θ parameter in the MA(1) model. So there are two parameters that define an MA(1) model: the coefficient θ and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex].
Some authors prefer to parameterize the MA(1) model as
where θ0 and θ1 are real-valued parameters. We avoid this parameterization because the θ0 parameter is redundant in the sense that the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex] is absorbed into the θ0 parameter. Also, some authors use a - rather than a + between two terms on the right-hand side of the model.
To illustrate the thinking behind the MA(1) model in a specific context, let Xt represent the monthly unemployment, as a percentage, in month t. The MA(1) model indicates that this month's unemployment, denoted by Xt, equals θ multiplied by last month's random white noise term, [latex]\theta Z_{t - 1}[/latex], plus this month's random white noise term Zt.
MA(1) models are used less often than autoregressive models, and this is partly due to more limited potential shapes for the population autocorrelation function, as will be seen next.
Stationarity and the Population Autocorrelation Function
One initial important question concerning the MA(1) model is whether or not the model is stationary. Rather than appealing to Theorem 8.4, we show this below using first principles. Recall from Definition 7.6 that a time series model is stationary if (a) the expected value of Xt is constant for all t, and (b) the population covariance between Xs and Xt depends only on the lag [latex]|t - s|[/latex]. The expected value of Xt is
for all values of the parameters θ and [latex]\sigma _ Z ^ {\, 2}[/latex], and all values of t. Using the defining formula for population covariance, the population autocovariance function is
Since [latex]E \left[ X_t \right] = 0[/latex] for all values of t and the population autocovariance function depends only on the lag [latex]|t - s|[/latex], we conclude that the MA(1) time series model is stationary. Furthermore, the population autocovariance function can be expressed in terms of the lag k as
Dividing by the population autocovariance function by [latex]\gamma(0) = V \left[ X_t \right] = \left( 1 + \theta ^ 2 \right) \sigma _Z ^ {\, 2}[/latex] gives the population autocorrelation function
This derivation constitutes a proof of the following result.
So the population autocorrelation function consists of a single nonzero value at lag 1 for a nonzero parameter θ and zero values thereafter. Six important observations concerning this population autocorrelation function are given below.
-
- The sign of [latex]\rho(1)[/latex] is the same as the sign of θ.
- The population autocorrelation function cuts off after lag 1 for an MA(1) time series model. The time series model has a “memory” of just one time period. Figure 9.35 illustrates the relationship between the white noise values [latex]\left\{ Z_t \right\}[/latex] and the MA(1) time series observations [latex]\left\{ X_t \right\}[/latex]. Observations of the time series that are two or more time periods apart, such as X2 and X4, have no white noise terms in common, so the lag 2 population autocorrelation, [latex]\rho(2)[/latex], is zero. The third observation in the time series X3, for example, shares the white noise term Z2 with X2 and the white noise term Z3 with X4, but is not affected by any white noise terms before Z2 or after Z3.

Figure 9.35: Relationship between white noise [latex]\left\{ Z_t \right\}[/latex] and [latex]\left\{ X_t \right\}[/latex] for an MA(1) model. - The lag 1 population autocorrelation [latex]\rho(1) = \theta / \left(1 + \theta ^ 2 \right)[/latex] can be written as a quadratic equation in θ as
For nonzero values of θ, the two roots of this quadratic equation are both positive or both negative. Furthermore, a little algebra reveals that the product of the two roots of this quadratic equation equals 1. Figure 9.36 shows the parabolas associated with this quadratic equation for [latex]\rho(1) = 2 / 5[/latex] (with associated roots [latex]\theta = 1 / 2[/latex] and [latex]\theta = 2[/latex]) and [latex]\rho(1) = -2 / 5[/latex] (with associated roots [latex]\theta = -1 / 2[/latex] and [latex]\theta = -2[/latex]).
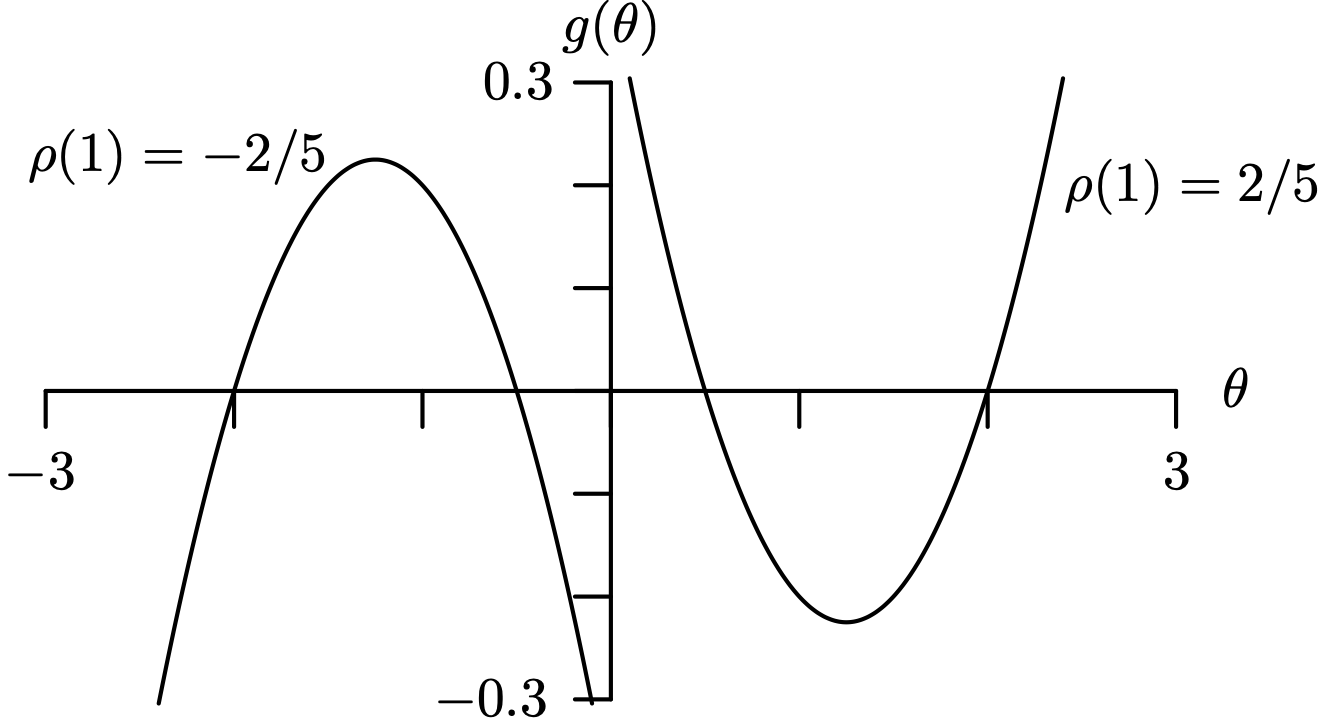
Figure 9.36: The parabola [latex]g(\theta) = \rho(1) \theta ^ 2 - \theta + \rho(1)[/latex] for [latex]\rho(1) = 2 / 5[/latex] and [latex]\rho(1) = - 2 / 5[/latex]. Long Description for Figure 9.36
The horizontal axis theta ranges from negative 3 to 3 in increments of 1 unit. The vertical axis g of theta ranges from negative 0.3 to 0.3 in increments of 0.1 units. A convex parabola for rho of 1 value 2 over 5 has the lowest point at (1.25, negative 0.2) and intersects the horizontal axis at (0.5, 0) and (2, 0). A concave parabola for rho of 1 value negative 2 over 5 has the highest point at (negative 1.25, 0.2) and intersects the horizontal axis at (negative 0.2, 0) and (negative 0.5, 0). All data are estimated.
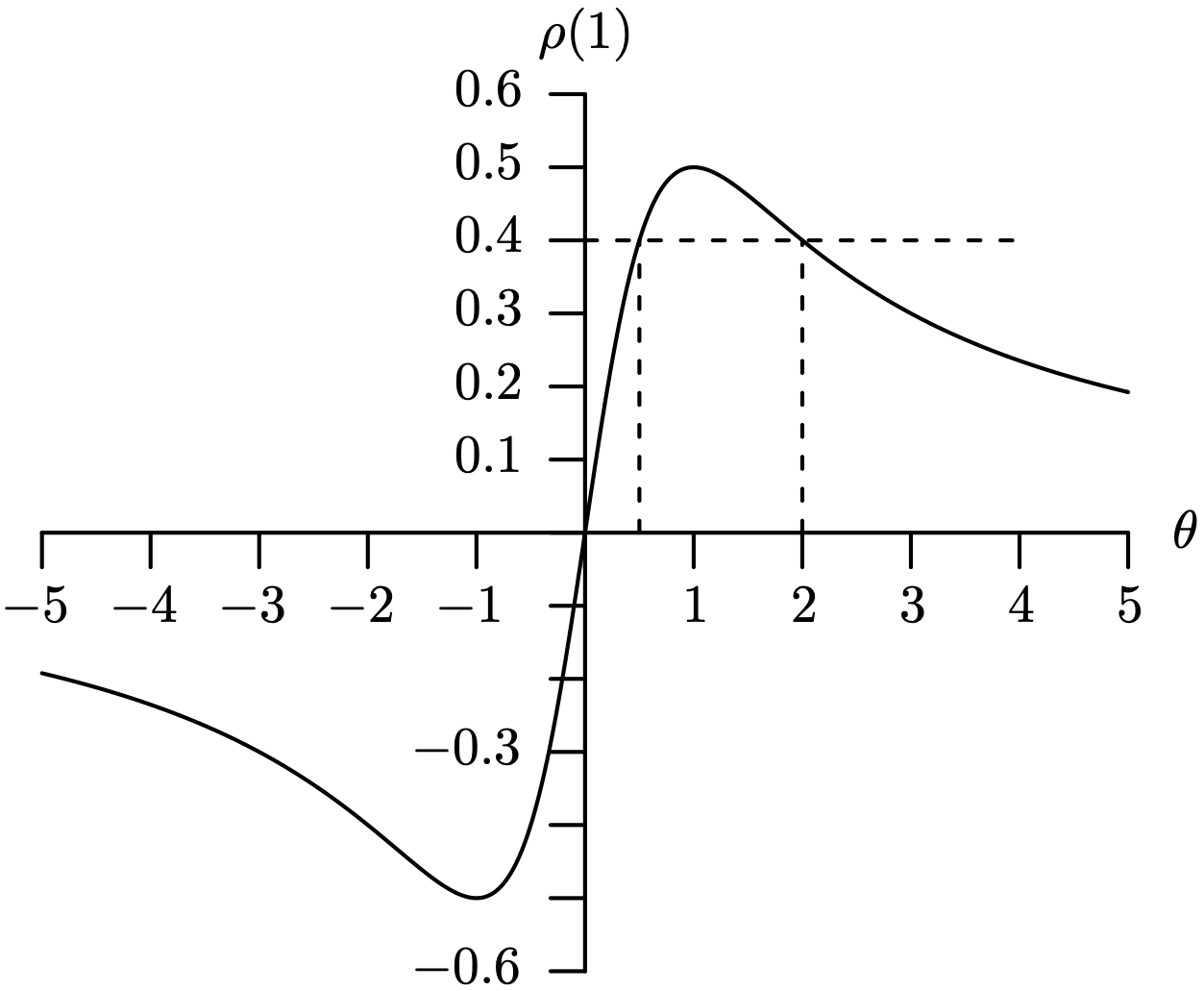
Figure 9.37: Graph of [latex]\rho(1) = \theta / \left( 1 + \theta ^ 2 \right)[/latex] versus θ for an MA(1) time series model. Long Description for Figure 9.37
The horizontal axis theta ranges from negative 5 to 5 in increments of 1 unit. The vertical axis rho of 1 ranges from negative 0.6 to 0.6. The concave curve decreases in quadrant 3 from (negative 5, negative 0.2) to the lowest point (negative 1, negative 0.5), increases through the origin to the highest point (1, 0.5), and decreases as a convex curve to (5, 0.2). A dashed horizontal line is drawn at rho of 1 value 0.4, intersecting the curve twice at theta equals 0.5 and 2. All data are estimated.
- The value [latex]\rho(1)[/latex] must lie in the interval [latex]-1 / 2 \le \rho(1) \le 1 / 2[/latex]. This can be seen in the plot of [latex]\rho(1) = \theta / \left( 1 + \theta ^ 2 \right)[/latex] versus θ given by the solid curve in Figure 9.37, which indicates that [latex]\rho(1)[/latex] is minimized at [latex]\rho(1) = - 1 / 2[/latex] when [latex]\theta = -1[/latex] and maximized at [latex]\rho(1) = 1 / 2[/latex] when [latex]\theta = 1[/latex]. This constraint means that the MA(1) model is more limited in application than the autoregressive models from the previous chapter. In order to fit an MA(1) model to observed time series values [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], it must be the case that (a) the length of the time series n is large enough (about [latex]n = 50[/latex] or [latex]n = 60[/latex]) to use an ARMA model, (b) the sample autocorrelation function has a single statistically significant spike at lag 1, and (c) the statistically significant spike at lag 1 satisfies [latex]-1 / 2 \le r_1 \le 1 / 2[/latex] to be compatible with the constraint [latex]-1 / 2 \le \rho(1) \le 1 / 2[/latex].
- Figure 9.37 also reveals a more subtle aspect of the population lag 1 autocorrelation. Notice that for [latex]\theta = 1 / 2[/latex], the population lag 1 autocorrelation is [latex]\rho(1) = 2 / 5[/latex]. But for [latex]\theta = 2[/latex], the population lag 1 autocorrelation is also [latex]\rho(1) = 2 / 5[/latex]. The geometry associated with these two values of θ resulting in the same value for [latex]\rho(1)[/latex] is indicated by the dashed lines in Figure 9.37. This problem is not just limited to [latex]\theta = 1 / 2[/latex] and [latex]\theta = 2[/latex]; there are an infinite number of pairs of θ values that will result in the same population lag 1 autocorrelation function value. More generally, the MA(1) model
and the MA(1) model
have identical population autocorrelation functions. This means that there is not a one-to-one correspondence between a particular value of θ and the associated value of [latex]\rho(1)[/latex]. This brings up the notion of invertibility, which was defined in Definition 8.3. An invertible time series model has a unique value of θ in the MA(1) model corresponding to a particular population autocorrelation function.
Invertibility
All MA(1) models are stationary per Theorem 8.3 because there are a finite number of moving average terms in Definition 9.4. Recall from Definition 8.3 that an ARMA(p, q) time series model for [latex]\left\{ X_t \right\}[/latex] is invertible if the white noise term at time t can be expressed as
where the coefficients πj satisfy
There are no restrictions on θ necessary to ensure stationarity for an MA(1) model. However, it can be advantageous to restrict the values of θ in order to achieve invertibility. Returning to Figure 9.37, we can use the definition of invertibility to determine whether we use [latex]|\theta| < 1[/latex] or [latex]| \theta | > 1[/latex] for the invertibility region for an MA(1) model.
Just as we were able to write an AR(1) time series model as an MA(∞) time series model in Section 9.1.1, we now perform the algebraic steps necessary to write an MA(1) time series model as an AR(∞) time series model. We want to write Zt in terms of current and previous values of Xt as shown in Definition 8.3. To begin, recall that the MA(1) model given by
can be shifted in time and is equally valid for other t values, for example,
These formulas can be solved for [latex]Z_{t - 1}[/latex], [latex]Z_{t - 2}[/latex], [latex]\ldots[/latex] as
Making successive substitutions into the MA(1) model results in
This can be recognized as an AR(∞) time series model.
Representing an MA(1) model as an AR(∞) model is known as duality. Solving this equation for Zt gives
which is the form required for Definition 8.3. So the coefficients [latex]\pi_0, \,\pi_1, \, \pi_2, \, \ldots[/latex] for the MA(1) model from Definition 8.3 are
or in general, [latex]\pi_j = \left( - \theta \right) ^ j[/latex], for [latex]j = 0, \, 1, \, 2, \, \ldots[/latex]. Definition 8.3 requires that
to achieve stationarity. This summation is a geometric series that converges when [latex]|\theta| < 1[/latex], so this is the invertibility region for an MA(1) model.
The invertibility criterion [latex]-1 < \theta < 1[/latex] ensures that each value of θ in the interval corresponds to a unique MA(1) time series model. Stated in another fashion, invertibility implies that there is a one-to-one correspondence between the value of the θ parameter and the population autocorrelation function.
The MA(1) time series model can be written in terms of the backshift operator B as
Doubling up the use of θ as a function name, the expression
is the characteristic polynomial for the MA(1) model. Notice that the MA(1) model is invertible when [latex]| \theta | < 1[/latex], which corresponds to the root of [latex]\theta(B) = 0[/latex] falling outside of the interval [latex][-1, \, 1][/latex]. Solving [latex]\theta(B) = 1 + \theta B = 0[/latex] results in [latex]B = - 1 / \theta[/latex]. This notion will be generalized in the next two subsections for higher-order MA models as the roots of [latex]\theta(B) = 0[/latex] falling outside of the unit circle in the complex plane to establish invertibility.
Now that stationarity for all MA(1) time series models has been established, the condition for invertibility has been established, and the population autocorrelation function has been derived, we turn to determining the partial autocorrelation function.
Population Partial Autocorrelation Function
The population partial autocorrelation function can be determined by using the defining formula in Definition 7.4. The lag zero population partial autocorrelation is [latex]\rho ^ * (0) = 1[/latex]. The lag one population partial autocorrelation is [latex]\rho ^ * (1) = \rho(1) = \theta / \left( 1 + \theta ^ 2 \right)[/latex]. After a little algebra, the lag two population partial autocorrelation is
The lag three population partial autocorrelation is
This pattern generalizes to the lag k population partial autocorrelation
for [latex]k = 1, \, 2, \, \ldots[/latex], which can also be written as
for [latex]k = 1, \, 2, \, \ldots[/latex]. This constitutes a proof of the following result.
When [latex]\theta = 0[/latex], both the population autocorrelation function and the partial autocorrelation function have just a single spike at [latex]\rho(0) = \rho ^ * (0) = 1[/latex]; the MA(1) model reduces to just white noise in this case. When [latex]0 < \theta < 1[/latex], [latex]\rho(1) > 0[/latex] and [latex]\rho^*(k)[/latex] tails out and alternates in sign. When [latex]-1 < \theta < 0[/latex], [latex]\rho(1) < 0[/latex] and [latex]\rho^*(k)[/latex] tails out and is negative for [latex]k = 1, \, 2, \, \ldots[/latex].
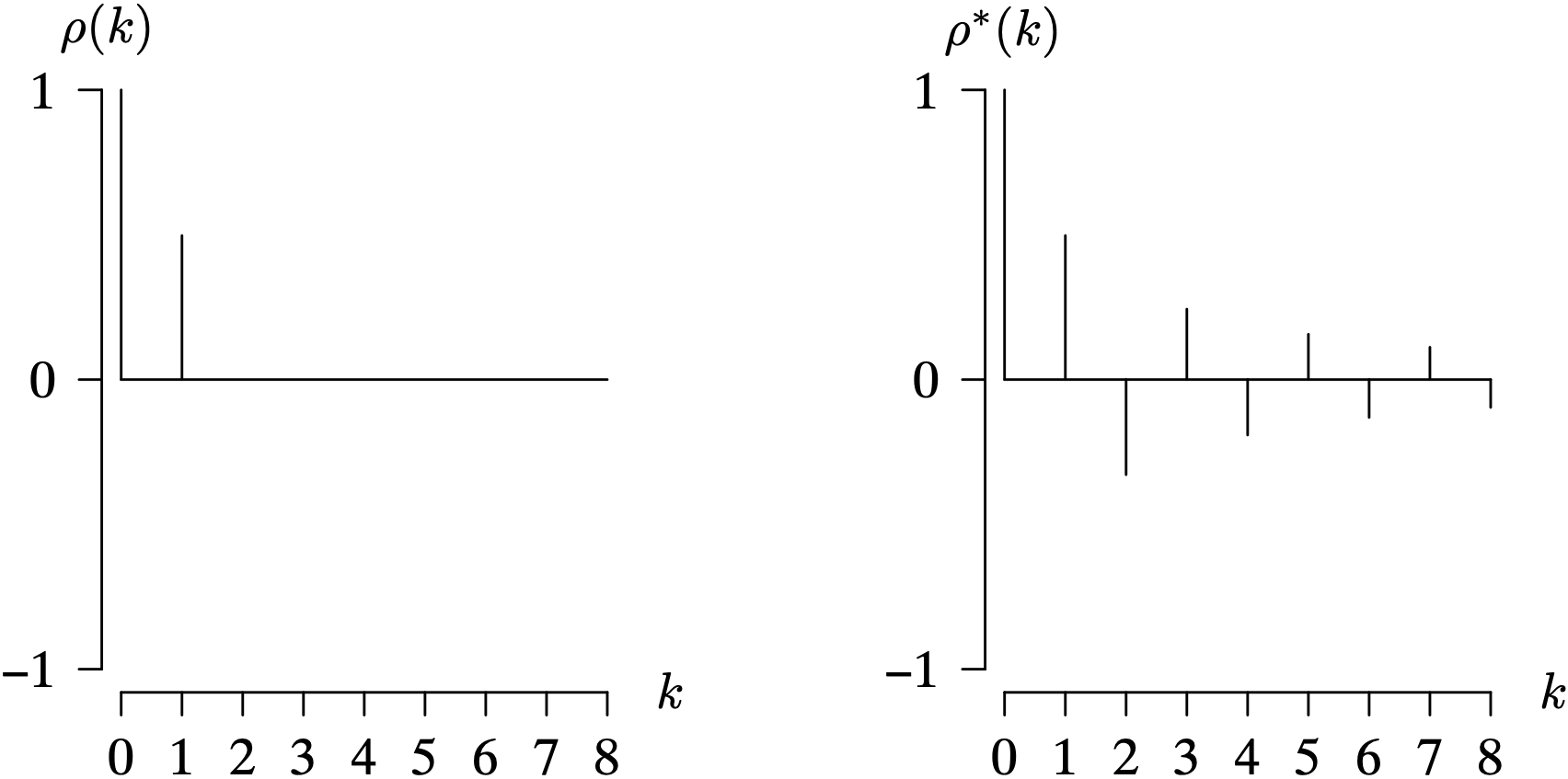
Long Description for Figure 9.38
In the first correlogram, the horizontal axis k ranges from 0 to 8 in increments of 1 unit. The vertical axis rho of k ranges from negative 1 to 1 in increments of 1 unit. A horizontal line is drawn at rho subscript k value 0. The values of rho of k are 1 and 0.5, respectively for k values 0 and 1. In the second correlogram, the horizontal axis k ranges from 0 to 8 in increments of 1 unit. The vertical axis rho star of k ranges from negative 1 to 1. This function follows a damped sinusoidal fashion, with alternate signs and decreasing magnitude. All data are estimated.
The Shifted MA(1) Model
The population mean function for the MA(1) model is [latex]E \left[ X_t \right] = 0[/latex], which is not of much use in practice because most real-world time series are not centered around zero. Adding a third parameter μ to overcome this shortcoming results in the enhanced MA(1) model
which has population mean function [latex]E \left[ X_t \right] = \mu[/latex] and population autocorrelation function and population autocorrelation function given in Theorems 9.25 and 9.28 because population variance and covariance are unaffected by a shift in the time series model. There are now three parameters for the time series model: μ, θ, and [latex]\sigma _ Z ^ {\, 2}[/latex].
Simulation
An MA(1) time series can be simulated by appealing to the defining formula for the MA(1) model from Definition 9.4:
The algorithm given below generates an initial white noise value Z0, and then uses an additional n white noise terms [latex]Z_1, \, Z_2, \, \ldots, \, Z_n[/latex] to generate the time series values [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] using the MA(1) defining formula. Indentation denotes nesting in the algorithm.
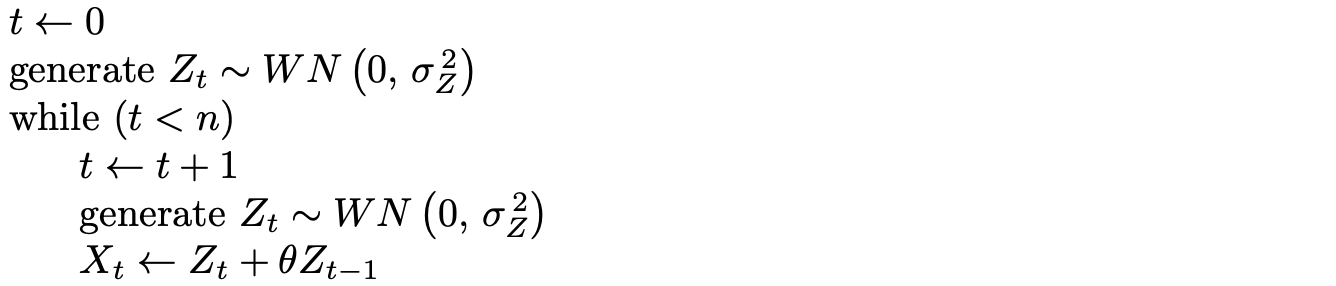
The three-parameter shifted MA(1) time series model that includes a population mean parameter μ can be simulated by simply adding μ to each time series observation generated by this algorithm. So to generate a realization of an MA(1) time series model in R, we must define (a) the value of θ, (b) the distribution of the white noise, (c) the value of [latex]\sigma _Z ^ {\, 2}[/latex], and, if this is a shifted MA(1) model, (d) the value of the shift parameter μ.
Having established the probabilistic properties of the MA(1) model, we now turn to statistical topics, beginning with the estimation of the model parameters.
Parameter Estimation
There are several techniques for estimating the parameters in an MA(1) model; as was the case for the autoregressive models, we look at the method of moments, least squares, and maximum likelihood estimation techniques separately. Parameter estimation is more difficult for moving average models, as numerical methods are typically required to calculate the parameter estimates.
Approach 1: Method of moments. We begin with the shifted MA(1) model from Definition 9.4:
We want to estimate the three unknown parameters μ, θ, and [latex]\sigma _ Z ^ {\, 2}[/latex] from an observed time series [latex]\left\{ x_t \right\}[/latex]. In the case of the shifted MA(1) model, we match the population and sample (a) first-order moments, (b) second-order moments, and (c) lag 1 autocorrelation. These will be written with upper case values Xt although these will be replaced with numeric values xt for a particular observed time series. Placing the population moments of the left-hand side of the equation and the associated sample moments on the right-hand side of the equation results in three equations in three unknowns:
or
The third equation is a quadratic equation in θ:
which corresponds to the parabolas in Figure 9.36, except that [latex]\rho(1)[/latex] is replaced by r1. Using the quadratic formula, the product of the two roots
equals 1, so the root that falls within the invertibility region [latex]-1 < \hat \theta < 1[/latex] should be chosen. Some algebra shows that this can be done by always selecting the minus in the ± portion of the formula. Once the point estimator [latex]\hat \theta[/latex] has been chosen, the first two equations can be solved as
It appears that we have closed-form solutions to the method of moments estimators, but there is a subtle wrinkle in this derivation. Because of random sampling variability there is a chance that the lag 1 sample autocorrelation r1 might be greater than [latex]1 / 2[/latex] or less than [latex]-1 / 2[/latex], even if the population time series model truly is a shifted MA(1) model satisfying the invertibility criterion [latex]-1 < \theta < 1[/latex]. In this case the quadratic formula yields complex roots. So the method of moments parameter estimation approach is recommended for initial parameter estimates only if the constraint [latex]|r_1| < 1 / 2[/latex] stated in the result that follows is met.
Thus, the method of moments point estimators in Theorem 9.30 should only be used for determining initial estimators of μ, θ, and [latex]\sigma _ Z ^ {\, 2}[/latex] from [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] when the following criteria are met:
- the number of observations in the time series is greater than about [latex]n = 60[/latex] or [latex]n = 70[/latex],
- the time series appears to be stationary,
- the sample autocorrelation function has a single statistically significant spike at lag 1,
- the sample partial autocorrelation function tails out, and
- [latex]-1 / 2 < r_1 < 1 / 2[/latex].
The method of moments estimators are generally used to find initial point estimates for the parameters in an MA(1) model, which are subsequently used in an iterative scheme to find the least squares or maximum likelihood estimators. This will be illustrated next on a time series consisting of chemical yields.
Approach 2: Least squares. Consider the shifted stationary MA(1) model
from Theorem 9.29. For least squares estimation, we first establish the sum of squares S as a function of the parameters μ and θ. Numerical methods are required to determine the least squares estimators of μ and θ. Once these least squares estimators have been determined, the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex] will be estimated.
Solving the shifted MA(1) model defining formula for Zt results in
Seeding this recursive formula with [latex]Z_0 = 0[/latex] gives the residuals
Thus, the sum of squared errors is
Numerical methods are required to find the parameter estimates. This will be illustrated next for the time series of chemical yields.
Approach 3: Maximum likelihood estimation. We use the arima function to do the heavy lifting with respect to the estimation of the parameters in the MA(1) time series model via maximum likelihood. In addition to the point estimates, confidence intervals are based on the asymptotic distribution of the maximum likelihood estimator [latex]\hat \theta[/latex], which for large values of n is
So when the parameter θ is estimated by maximum likelihood from a time series, an asymptotically exact [latex]{100(1 - \alpha)}\%[/latex] confidence interval for θ is given in the result below. It is based on the consistency and the asymptotic normality of maximum likelihood estimators, which in this case implies that
Replacing θ by its maximum likelihood estimator in the variance yields the following result.
The formula for the confidence interval from Theorem 9.31 will be illustrated for the chemical yield data from the previous two examples.
The parameter estimates using the method of moments, least squares, and maximum likelihood estimation from the previous three examples are summarized in Table 9.16. Notice that the least squares and maximum likelihood estimates of θ differ significantly from the associated method of moments estimator of θ.
|
Method |
[latex]\hat \mu[/latex] |
[latex]\hat \theta[/latex] |
[latex]\hat \sigma _ Z ^ {\, 2}[/latex] |
|---|---|---|---|
|
Method of moments |
84.1 |
−0.318 |
7.50 |
|
Ordinary least squares |
84.1 |
−0.483 |
5.61 |
|
Maximum likelihood estimation |
84.1 |
−0.480 |
7.07 |
In the interest of brevity, we leave the model assessment, model selection, and forecasting steps of the process for the chemical yields time series as an exercise. The derivations for these procedures follow along the same lines as those for the autoregressive models from the previous section.
This subsection has introduced the MA(1) time series model. The key results for an MA(1) model are listed below.
- The standard MA(1) model can be written algebraically and with the backshift operator B as
where [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex], [latex]\sigma _ Z ^ {\, 2} > 0[/latex], and [latex]\theta(B) = 1 + \theta B[/latex] (Definition 9.4).
- The shifted MA(1) model can be written algebraically and with the backshift operator B as (Theorem 9.29)
- The MA(1) model is stationary for all finite real-valued parameters θ and [latex]\sigma _ Z ^ {\, 2}[/latex] (Theorem 9.25).
- The MA(1) model is invertible when [latex]-1 < \theta < 1[/latex] (Theorem 9.27).
- The MA(1) model can be written as an AR(∞) model when [latex]-1 < \theta < 1[/latex] as (Theorem 9.26)
- The MA(1) model lag 1 population autocorrelation is [latex]\rho(1) = \theta / \left( 1 + \theta ^ 2 \right)[/latex], and [latex]\rho(k) = 0[/latex] for [latex]k = 2, \, 3, \, \ldots[/latex] (Theorem 9.25). The lag 1 population autocorrelation satisfies the inequality [latex]-1 / 2 \le \rho(1) \le 1 / 2[/latex] (Figure 9.37).
- The MA(1) lag k population partial autocorrelation for [latex]-1 < \theta < 1[/latex] is
for [latex]k = 1, \, 2, \, \ldots[/latex] (Theorem 9.28).
- A time series of [latex]n + 1[/latex] white noise values [latex]Z_0, \, Z_1, \, Z_2 , \, \ldots, \, Z_n[/latex] can be converted to n simulated observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] by using the MA(1) defining formula [latex]X_t = Z_t + \theta Z_{t - 1}[/latex].
- The parameters in the MA(1) model can be estimated via the method of moments, least squares estimation, and maximum likelihood estimation.
9.2.2 The MA(2) Model
The additional term in the MA(2) model gives it increased flexibility over the associated MA(1) model.
An observed value in the time series, Xt, is given by the current white noise term, plus the parameter θ1 multiplied by the white noise term from one time period ago, plus the parameter θ2 multiplied by the white noise term from two time periods ago. So there are three parameters that define an MA(2) model: the coefficients θ1 and θ2, and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. As was the case of the MA(1) model, some authors use a - rather than a + between three terms on the right-hand side of the model.
The probabilistic properties and statistical methods associated with an MA(2) model are straightforward generalizations of those properties and methods for the MA(1) model. Rather than deriving these results from first principles, we simply state several of these results without proof and then conduct a Monte Carlo simulation experiment which highlights issues that arise in model selection.
-
- The standard MA(2) model can be written algebraically and with the backshift operator B as
where [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex], [latex]\sigma _ Z ^ {\, 2} > 0[/latex], and [latex]\theta(B) = 1 + \theta_1 B + \theta_2 B ^ 2[/latex].
- The shifted MA(2) model can be written algebraically and with the backshift operator B as
- MA(2) models are stationary for all finite, real-valued parameters μ, θ1, θ2, and [latex]\sigma _ Z ^ {\, 2}[/latex].
- Just as the stationarity region for the AR(2) model has a triangular shape, the invertibility region for the MA(2) model also has a triangular shape defined by the three constraints
This region is an upside-down version of the region for an AR(2) time series model depicted in Figure 9.12. In other words, the triangles are equivalent when reflected vertically about the origin.
- The population autocovariance function is
- The population autocorrelation function is
- The population partial autocorrelation function of an MA(2) model can be determined by using the defining formula from Definition 7.8.
- A simulated realization [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] of a time series from an MA(2) model is generated by the following algorithm.
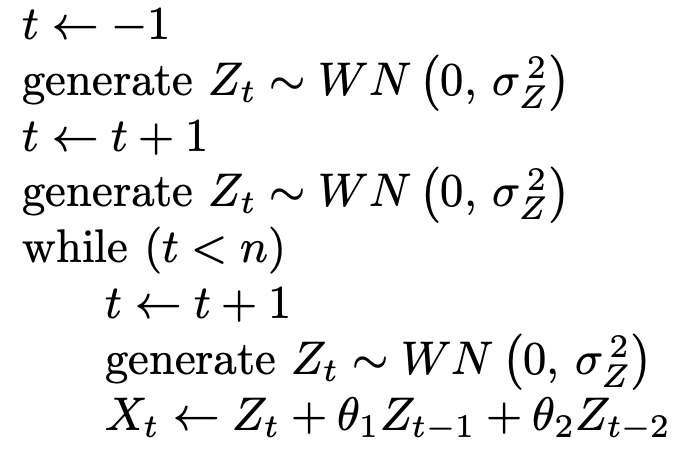
- The standard MA(2) model can be written algebraically and with the backshift operator B as
-
- The parameters of an MA(2) time series model can be estimated by the method of moments, least squares, and maximum likelihood estimation. As shown in the next example, the arima function can be used in R to calculate these parameter estimates.
The previous subsections have analyzed n observed values of a time series in order to determine an AR(p) or MA(q) model which adequately describes the probabilistic mechanism governing the observed time series. Instead of following this same pattern, we instead conduct a Monte Carlo simulation experiment that highlights weaknesses in the model selection process.
To summarize the models considered so far in this chapter, the AR(1), AR(2), MA(1), and MA(2) models are parsimonious in the sense that they have significant explanatory power with few parameters. By deriving the population autocorrelation function and partial autocorrelation function for these models, we now possess an inventory of possible shapes that guide us toward one particular time series model or another. Figure 9.43 gives examples of these shapes for various values of the parameters.
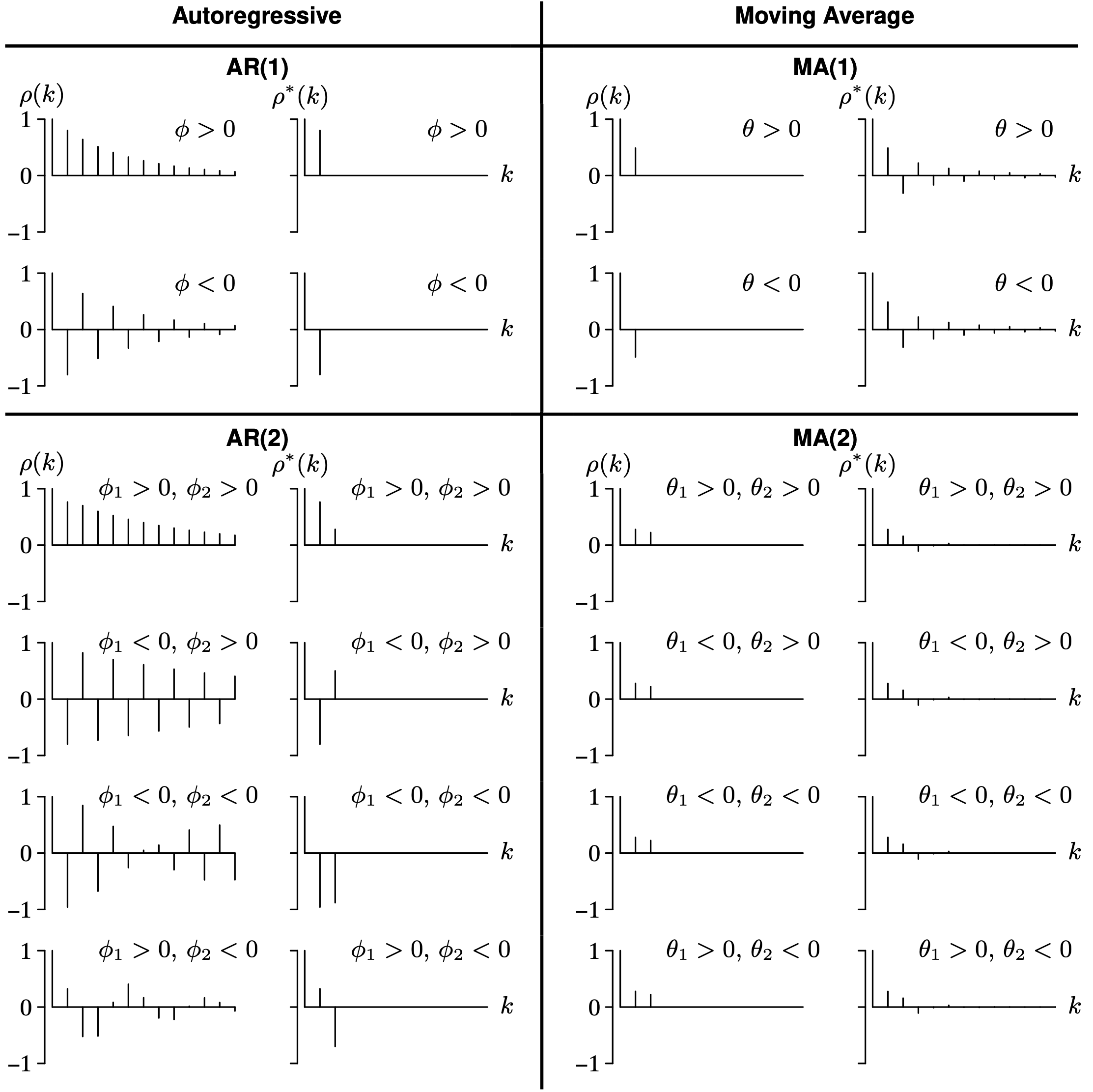
Long Description for Figure 9.43
The first column represents autoregressive models A R 1 and A R 2 while the second column represents moving average M A 1 and M A 2. Each column exhibits a correlogram for population autocorrelation function rho of k, and a partial autocorrelation function rho star of k. In each correlogram, the horizontal axis is k, and the vertical axis ranges from negative 1 to 1 in increments of 1 unit. A horizontal line is drawn at 0. For the A R 1 model, if phi is greater than 0, the rho of k values decreases from 1 to 0.2. The rho star of k values are 1 and 0.8 for the first two k values. For the A R 1 model, if phi is less than 0, the rho of k values alternate signs and follow a damped sinusoidal fashion with decreasing magnitude. The rho star of k values are 1 and negative 0.8 for the first two k values. For the A R 2 model, there are four cases. Case 2. If phi 1 is greater than 0 and phi 2 is greater than 0, the rho of k values decreases from 1 to 0.2. The rho star of k values decreases from 1 to 0.3 for the first three k values. Case 2. If phi 1 is less than 0 and phi is greater than 0, the rho of k values alternate signs and follows a damped sinusoidal pattern with decreasing magnitude. The rho star of k values are 1, negative 0.8, and 0.5, respectively for the first three k values. Case 3. If phi 1 is less than 0 and phi 2 is less than 0, rho of k values alternate signs with different magnitudes. The rho star of k values are 1, negative 1, and negative 0.8 for the first three k values. Case 4. If phi 1 is greater than 0 and phi 2 is less than 0, the rho of k values follows a damped sinusoidal fashion. The rho star of k values are 1, 0.2, and negative 0.6 for the first three k values. For the moving average M A 1 model, if theta is greater than 0, the rho of k values are 1 and 0.5 for the first 2 k values. The rho star of k values follows a damped sinusoidal fashion with decreasing magnitude. If theta is less than 0, the rho of k values are 1 and negative 0.5 for the first 2 k values. The rho star of k values follows a damped sinusoidal fashion with decreasing magnitude. For the moving average M A 2 model, there are four cases. Case 1: theta 1 greater than 0, theta 2 greater than 0. Case 2. theta 1 less than 0 and theta 2 greater than 0. Case 3. theta 1 less than 0 and theta 2 less than 0. Case 4. theta 1 greater than 0 and theta 2 less than 0. In all four cases, the rho of k values are 1, 0.2, and 0.15 for the first three k values. In all four cases, the rho star of k values is 1, 0.2, 0.1, and negative 0.05 for the first four k values. All data are estimated.
9.2.3 The MA(q) Model
The MA(1) and MA(2) models introduced in the previous two subsections generalize to the MA(q) model defined in this section.
An observed value in the time series, Xt, is given by the current white noise term plus a linear combination of the q previous white noise terms. So there are [latex]q + 1[/latex] parameters that define an MA(q) model: the coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex]. As was the case of the MA(1) and MA(2) models, some authors use a - rather than a + between terms on the right-hand side of the model.
The probabilistic properties and statistical methods associated with an MA(q) model are determined in the usual fashion. Here are several of these results stated without proof.
- The population mean and variance of Xt are easily calculated by taking the expected value and the population variance of both sides of the equation given in Definition 9.6:
and
- The standard MA(q) model can be written algebraically and with the backshift operator B as
where [latex]Z_t \sim WN \left( 0, \, \sigma _Z ^ {\, 2} \right)[/latex], [latex]\sigma _ Z ^ {\, 2} > 0[/latex], and [latex]\theta(B) = 1 + \theta_1 B + \theta_2 B ^ 2 + \cdots + \theta_q B ^ q[/latex].
- The shifted MA(q) model can be written algebraically and with the backshift operator B as
- MA(q) models are stationary for all finite, real-valued parameters μ, [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex].
- MA(q) models are invertible when the q roots of the characteristic equation
all lie outside of the unit circle in the complex plane.
- The population autocovariance function is
This can be written more compactly as
where [latex]\theta_0 = 1[/latex].
- The population autocorrelation function is
As expected, the population autocorrelation function cuts off after lag q.
- The population partial autocorrelation function of an MA(q) model can be determined by using the defining formula from Definition 7.8.
- A simulated realization [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] of a time series from an MA(q) model is generated by the following algorithm.
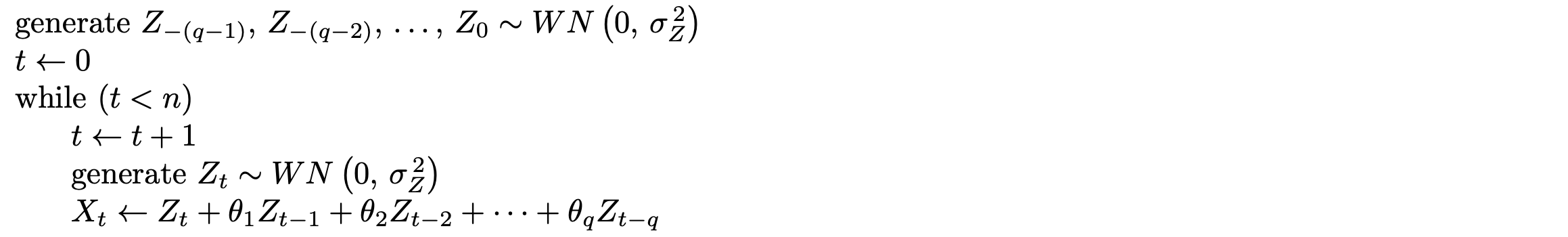
- The parameters of an MA(q) time series model can be estimated by the method of moments, least squares, and maximum likelihood estimation. The arima function can be used in R to calculate these parameter estimates for particular values of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex].
Table 9.18 shows some of the symmetry between autoregressive and moving average models. When one aspect of the time series model is easier to derive for one of the models, it is often more difficult to derive for the analogous time series model. The population autocorrelation function for an MA(q) model is closed form, for example, but the population autocorrelation function for an AR(p) model requires solving the Yule–Walker equations. As a second example on the statistical side, the least squares estimators for the AR(1) model are closed form, but the least squares estimators for the MA(1) model require numerical methods.
|
Autoregressive: AR(p) |
Moving Average: MA(q) |
|
|---|---|---|
|
Model definition |
[latex]\phi(B) X_t = Z_t[/latex] |
[latex]X_t = \theta(B) Z_t[/latex] |
|
Characteristic polynomial |
[latex]\phi(B) = 1 - \phi_1 B - \phi_2 B ^ 2 - \cdots - \phi_p B ^ p[/latex] |
[latex]\theta(B) = 1 + \theta_1 B + \theta_2 B ^ 2 + \cdots + \theta_q B ^ q[/latex] |
|
Stationarity condition |
[latex]\phi(B) = 0[/latex] roots outside of unit circle |
always stationary |
|
Invertibility condition |
always invertible |
[latex]\theta(B) = 0[/latex] roots outside of unit circle |
|
Equivalent model |
MA(∞) when stationary |
AR(∞) when invertible |
|
General linear model π weights |
finite series |
infinite series |
|
General linear model [latex]\psi[/latex] weights |
infinite series |
finite series |
|
Shape of [latex]\rho(k)[/latex] |
tails out |
cuts off after lag q |
|
Shape of [latex]\rho^*(k)[/latex] |
cuts off after lag p |
tails out |
|
Simulating a realization |
warm up period needed |
no warm up period needed |
9.3 ARMA([latex]p, \, q[/latex]) Models
The autoregressive and moving average models outlined in the previous two sections often prove to be inadequate time series models in a particular application. Occasions arise in which the best model for a time series involves both autoregressive and moving average terms. Recall from Definition 8.4 that an ARMA(p, q) time series model with p autoregressive terms and q moving average terms is
$$
X_t = \rlap{\overbrace{\phantom{
\phi_1 X_{t - 1} +
\phi_2 X_{t - 2} +
\cdots +
\phi_p X_{t - p} +
\phantom{Z_t}}}^{\hbox{autoregressive portion}}}
\phi_1 X_{t - 1} +
\phi_2 X_{t - 2} +
\cdots +
\phi_p X_{t - p} +
\underbrace{
Z_t +
\theta_1 Z_{t - 1} +
\theta_2 Z_{t - 2} +
\cdots +
\theta_q Z_{t - q}}_{\hbox{moving average portion}},
$$
where [latex]\left\{ X_t \right\}[/latex] is the time series of interest, [latex]\left\{ Z_t \right\}[/latex] is a time series of white noise, [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] are real-valued parameters associated with the AR portion of the model, and [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex] are real-valued parameters associated with the MA portion of the model. The ARMA(p, q) model can be written more compactly as
where [latex]\phi(B)[/latex] and [latex]\theta(B)[/latex] are the characteristic polynomials defined by
and
This model on its own is of little practical use because most real-world time series are not centered around [latex]E[X_t] = 0[/latex]. Using the compact notation for the ARMA(p, q) time series model, a shift parameter μ is easily added:
So there are [latex]p + q + 2[/latex] parameters that define a shifted ARMA(p, q) time series model: the p autoregressive coefficients [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex], the q moving average coefficients [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_q[/latex], the shift parameter μ, and the population variance of the white noise [latex]\sigma _ Z ^ {\, 2}[/latex].
Recall from Table 9.7 in Example 9.20 that the ARMA(1, 1) model fitted by maximum likelihood estimation gave a slightly lower AIC than the associated AR(2) model when applied to the Lake Huron level time series. This section will consist of one long example that concerns the fitting and assessing this ARMA(1, 1) model to determine whether it is an adequate model for the Lake Huron levels. Rather than deriving all of the probabilistic properties and statistical methods for the ARMA(1, 1) model, the arima function in R will be used to perform the fitting, leaving the details to the reader. By default, the arima function (a) ignores external regressor variables, (b) ignores seasonal variation, (c) includes a shift parameter μ, (d) uses the same parameterization for the ARMA(p, q) process as that used in this text, (e) transforms the AR parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] if necessary so that they stay in the stationarity region, and (f) uses a conditional sum of squares method as initial parameter estimates, then returns the maximum likelihood estimators.
ARMA modeling can achieve population autocorrelation function and population partial autocorrelation function shapes that are not possible with just AR(p) and MA(q) models alone. For an ARMA(p, q) model with [latex]p > 0[/latex] and [latex]q > 0[/latex], both the population autocorrelation function and the population partial autocorrelation function tail off; neither of the two cut off after a certain lag.
An inherent weakness of ARMA modeling is that it requires stationarity. Many time series which occur in practice are not stationary, and the next section gives techniques that can be used to overcome this weakness.
9.4 Nonstationary Models
There are two commonly-used strategies for converting a nonstationary time series to a stationary time series in order to use ARMA modeling (or some other model which requires stationarity) on the resultant stationary time series. The first strategy is known as detrending. In this case, the modeler estimates the trend, and then fits a stationary time series model to the difference between the raw time series data and the estimated trend. The second strategy is known as differencing. In this case the modeler differences the time series one or more times, resulting in a stationary time series. Differencing carries the added benefit that no parameters are required other than the number of differences to take. The following two subsections consider these two strategies.
9.4.1 Removing Trends Via Regression
Although regression is not the only way to detrend a time series, it provides an adequate roadmap on how to proceed with the detrending process that generalizes to other mechanisms. This subsection illustrates detrending with a single example. We return for a third time to the Lake Huron levels which were fit to an AR(2) model in Section 9.1.2 and fit to an ARMA(1, 1) model in Section 9.3.
So far, there have been three different approaches to constructing a time series model for the Lake Huron levels:
- the shifted AR(2) model from Examples 9.14, 9.15, 9.16, 9.17, 9.18, 9.19, 9.20, and 9.21,
- the shifted ARMA(1, 1) model from Example 9.39, and
- the AR(2) model applied to the residuals from a simple linear regression from Example 9.40.
Which approach is preferred? Although the shifted AR(2) and shifted ARMA(1, 1) models fitted to the raw time series are roughly comparable and give nearly-identical forecasts, the shifted ARMA(1, 1) model has a slight edge for the following two reasons. First, from Table 9.7, the AIC value is 215 for the shifted AR(2) model and the AIC value is 214 for the shifted ARMA(1, 1) model. A smaller value implies a better fit. Second, the sum of squared residuals for the shifted AR(2) model is 46.9 and the sum of squared residuals for the shifted ARMA(1, 1) model is 46.5. A smaller sum of squared residuals for two models with an equal number of parameters is preferred. Both models have four parameters. These two sums of squared residuals for the two models are computed with the R statements
Although the differences between the AIC values and the sums of squares is small, the shifted ARMA(1, 1) model holds a slight edge.
The detrended model from Example 9.40, on the other hand, is preferred over the two stationary models because it explicitly models the decreasing lake levels over time. However, the fact that all of the forecasted values in the detrended model are low relative to the actual values in the years 1973 to 1982 is troubling. Could it be the case that there was no downward trend after all? At this point, some serious detective work is in order to see if the early values in the raw time series were elevated by some external influence and should not be included as a part of the time series. A rigorous search should be conducted for any external cause which might elevate the early values in the time series: excess rainfall, elevated temperatures, dredging, bridge projects, flow control projects, etc. As a particular instance, if the first 20 values of the time series can be eliminated due to the identification of an assignable cause for the years 1875–1894, for example, the p-value from simple linear regression testing for the statistical significance of the slope increases from a highly significant [latex]p = 4 \cdot 10 ^ {-8}[/latex] to a nonsignificant [latex]p = 0.11[/latex]. The downward trend would now be slight and a stationary model could be fitted to the remaining values in the time series.
Detrending has proved to be an effective method for transforming a nonstationary time series to a stationary time series. The second technique involves differencing.
9.4.2 ARIMA(p, d, q) Models
George Box and Gwilym Jenkins devised a time series modeling methodology known as ARIMA modeling. The I between AR and MA stands for integrated. These models are sometimes referred to as Box–Jenkins models. An ARIMA([latex]p, \, d, \, q[/latex]) time series model is one in which the dth-differenced times series, [latex]\nabla ^ d X_t[/latex], is an ARMA([latex]p, \, q[/latex]) time series. So ARIMA time series modeling uses repeated differencing of the raw time series in order to achieve a time series which appears to be stationary. ARMA modeling can be then applied to the resulting stationary time series.
Three key parameters in an ARIMA model are p, d, and q, which are all nonnegative integers. The parameter p is the number of coefficient parameters in the autoregressive portion of the model. The parameter d is the number of differences that are applied to the original time series in order to achieve stationarity. The parameter q is the number of coefficient parameters in the moving average portion of the model. So the general format for specifying an ARIMA model is ARIMA([latex]p, \, d, \, q)[/latex]. In addition to the parameters p, d, and q, there are [latex]p + q + 1[/latex] parameters that define an ARIMA([latex]p, \, d, \, q)[/latex] model: the p autoregressive parameters [latex]\phi_1, \, \phi_2, \, \ldots , \phi_p[/latex], the q moving average parameters [latex]\theta_1, \, \theta_2, \, \ldots , \theta_q[/latex], and the variance of the white noise [latex]\sigma _Z ^ {\, 2}[/latex]. As in the case of ARMA models, a shift parameter μ can be included in the model. If one or more of these parameters is zero, they are omitted from the specification. An IMA([latex]2, \, 1[/latex]) model, for example, has [latex]p = 0[/latex] autoregressive terms, [latex]d = 2[/latex] differences, and [latex]q = 1[/latex] moving average term. If a model only involves, for example, the autoregressive portion of the model with two terms (that is, no differencing and no moving average terms), then this model is specified as an AR(2) model. An ARMA([latex]p, \, q[/latex]) model is a special case of an ARIMA([latex]p, \, d, \, q[/latex]) model when [latex]d = 0[/latex].
ARIMA modeling will be illustrated by a simulation example that will reveal what a realization of an ARIMA process looks like, along with the R code required to fit these simulated values to an ARIMA model.
The ARIMA modeling process is adequate for nonstationary models but is not well-suited to handling cyclic variation. The SARIMA (seasonal autoregressive integrated moving average) model has been formulated to overcome this weakness.
An ARIMA model is a special case of a SARIMA model when [latex]P = D = Q = 0[/latex]. The ∇d term in the SARIMA model is associated with an ordinary difference; the [latex]\nabla _s ^ D[/latex] term is associated with a seasonal difference. Consider the inside portion of the SARIMA defining formula, [latex]\nabla ^ d \nabla ^ D _ s X_t[/latex], in a modeling setting in which monthly data is being collected and the modeler believes that there is cyclic annual variation, so [latex]s = 12[/latex]. In the case of [latex]d = 1[/latex] ordinary difference and [latex]D = 1[/latex] seasonal difference, this portion of the SARIMA defining formula becomes
The ∇ operator is being used to eliminate a linear trend and the ∇12 operator is being used to eliminate seasonality. The seasonal AR term [latex]\Phi \left( B ^ {\kern 0.04em s} \right)[/latex] and the seasonal MA term [latex]\Theta \left( B ^ {\kern 0.04em s} \right)[/latex] in Definition 9.8 provide autoregressive and moving average terms for observations that are s units distant in time.
To summarize this section, the modeling of a nonstationary time series involves the following steps.
- Plot the time series, noting any trends, seasonality, and nonconstant variance.
- Make the variance stable by applying appropriate transformations if necessary.
- Use detrending (possibly regression) or repeated differencing (to use an ARIMA model) to create a stationary time series.
- Plot the stationary time series along with its sample autocorrelation function and sample partial autocorrelation function.
- Hypothesize a tentative ARMA model for the stationary time series model. If there is a seasonal component, consider a SARIMA model on the transformed time series.
- Fit the tentative ARMA or SARIMA model. Perform the model assessment tests on the tentative time series model. If the fitted tentative ARMA or SARIMA model fails these tests, then hypothesize a new tentative model.
- Perform overfitting in the final model selection process to ensure that the best model has been selected.
- Apply the final time series model in the fashion dictated by the problem setting (this is often forecasting future values of the time series).
As illustrated in Example 9.42, time series modeling can be thought of as a step-by-step process of identifying a removing causes of variation in the time series (for example, trend, cycles, autocorrelation) until all that remains is white noise.
9.5 Spectral Analysis
In practice, many time series exhibit cyclic variation. The first two examples in Chapter 7 concerning monthly residential power consumption and monthly international airline travel both contain a cyclic component. The time series models derived from the general linear model do not explicitly consider cyclic variation; these models exist in what is known as the time domain. Spectral analysis considers modeling in the frequency domain. Spectral analysis decomposes a stationary time series into sinusoidal components (that is, sine and cosine functions) in order to identify frequencies associated with periodic components. Just as autoregressive models use regression on previous values of a time series in the time domain, spectral analysis uses regression on sine and cosine terms in the frequency domain.
Table 9.20 presents some new terminology that arises in spectral analysis and presents some analogies with known data analysis techniques. The column headings indicate that the three subsequent rows contain three application areas, three probability constructs, and their three statistical counterparts.
-
- The first row concerns the analysis of univariate data. In probability theory, several commonly-used probability distributions (for example, the exponential, normal, and binomial distribution) are investigated in order to build an inventory of potential probability distributions that might adequately describe a univariate data set. When an analyst encounters a univariate data set, one of the early steps in the analysis is to plot a histogram and compare its shape to the inventory of probability density functions associated with known probability distributions.
- The second row concerns time series analysis in the time domain. Shapes of the population autocorrelation function are derived for several commonly-used time series models (for example, the AR(2), MA(1), and ARMA(1, 1) models) in order to build an inventory of shapes such as those given in Figure 9.43 that might adequately describe the time series. When a time series analyst encounters time series observations, one of the early steps in the analysis is to plot the correlogram (a.k.a., the sample autocorrelation function) and compare its shape to the inventory of known population autocorrelation functions.
-
- The third row concerns time series analysis in the frequency domain. Shapes of the spectral density function are derived for several commonly-used time series models in order to build an inventory of shapes that might adequately describe the periodic nature of a time series. When a time series analyst encounters time series observations, one of the early steps is to plot the periodogram and compare its shape to the inventory of known spectral density functions.
|
Application area |
Probability construct |
Statistical counterpart |
|---|---|---|
|
univariate data |
probability density |
histogram |
|
time series analysis: |
population autocorrelation |
correlogram |
|
time series analysis: |
spectral density |
periodogram |
The next two subsections will focus on the spectral density function and its statistical counterpart, the periodogram.
9.5.1 The Spectral Density Function
The emphasis in the spectral analysis of a time series is the identification of the frequencies associated with cycles. The frequencies will be denoted here by ω. Just as the population autocorrelation function is the natural tool for identifying and quantifying autocorrelation in the time domain, the spectral density function is the natural tool for identifying and quantifying the frequencies associated with cyclic variation in the frequency domain. As seen in the following definition, the spectral density function can be written in terms of the population autocovariance function.
The interpretation of the spectral density function is that [latex]f(\omega) \Delta \omega[/latex] reflects the contribution of frequencies in the interval [latex](\omega, \, \omega + \Delta \omega)[/latex] to the variance of Xt for small values of [latex]\Delta \omega[/latex]. When [latex]f(\omega)[/latex] is high, then frequencies near ω have a large impact on Xt. When [latex]f(\omega)[/latex] is low, then frequencies near ω have a small impact on Xt. The upper limit of the support of the spectral density function, π, is known as the Nyquist frequency. Frequencies that exceed π are not captured by the spectral density function. This is not a universal choice for the definition of the spectral density function or the upper limit of its support. There are many valid alternative choices. A common alternative choice for the upper limit of the support is [latex]1 / 2[/latex].
The first example illustrates the calculation of a spectral density function for one of the most basic time series models.
The next example calculates the spectral density function of an MA(1) model. This particular model was chosen because it has an autocovariance function that cuts off after lag 1, which means that the summation given in Definition 9.9 consists of just a single term.
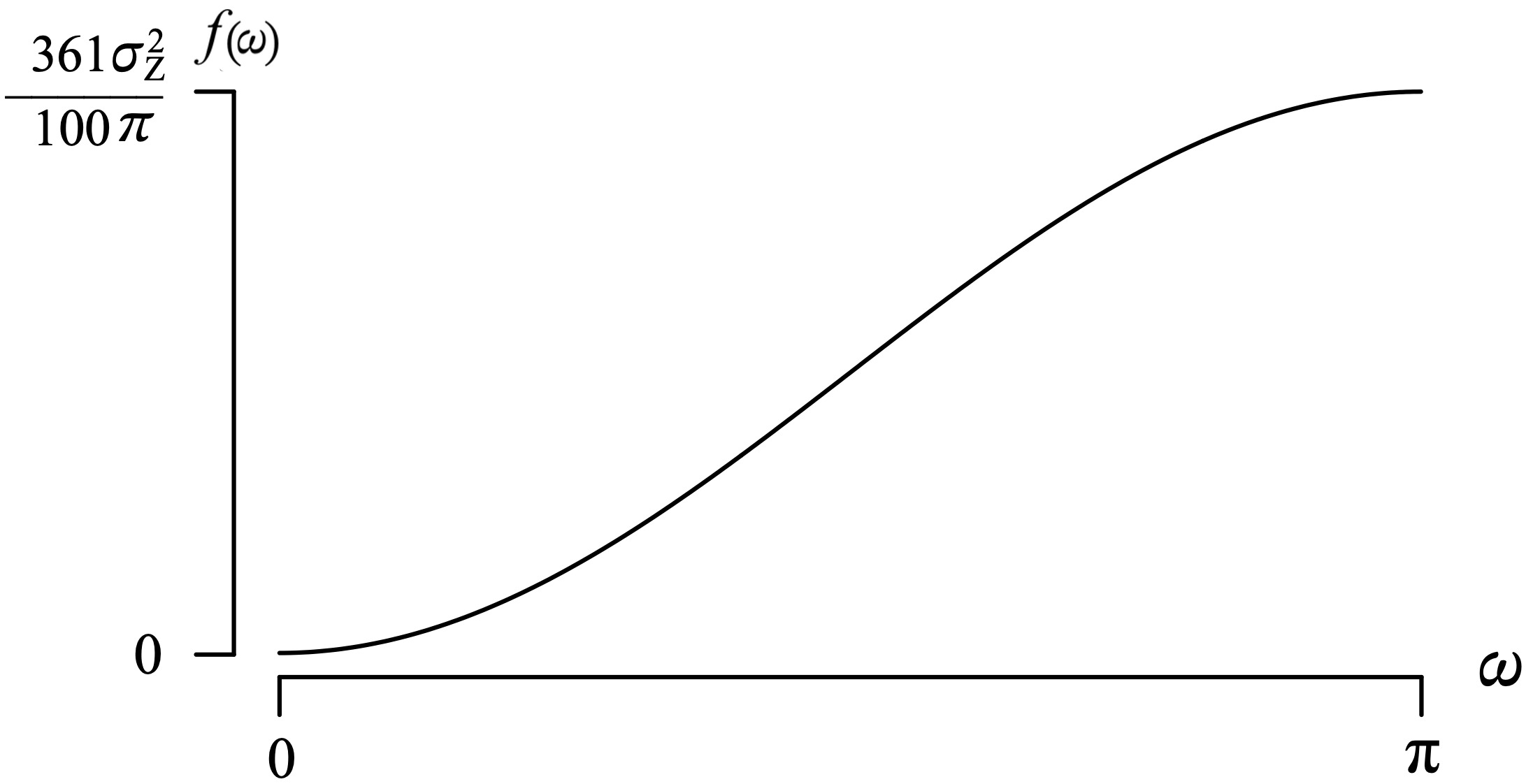
One common element from the spectral density functions given in the two previous examples is that they both integrate to [latex]\sigma _ X ^ {\, 2}[/latex]. This is true in general. Some time series analysts prefer to divide the spectral density function by [latex]\sigma _ X ^ {\, 2}[/latex] so that it will integrate to 1, making it a true probability density function. The normalized spectral density function is given by
Dividing both sides of the equation in Definition 9.9 by [latex]\gamma(0) = \sigma _ X ^ {\, 2}[/latex] gives
The associated normalized spectral cumulative distribution function is defined on the support of ω in the usual fashion as
One advantage of normalizing these two functions is that there is now a clean interpretation of [latex]F^*(\omega)[/latex]. For frequencies ω1 and ω2 satisfying [latex]0 < \omega_1 < \omega_2 < \pi[/latex], the expression [latex]F^*(\omega_2) - F^*(\omega_1)[/latex] denotes the proportion of the variance in [latex]\left\{ X_t \right\}[/latex] accounted for by frequencies on the interval [latex](\omega_1, \, \omega_2)[/latex].
9.5.2 The Periodogram
The periodogram is the statistical counterpart to the spectral density function. The periodogram estimates the spectral density function for all frequencies between 0 and π. The shape of the periodogram reflects the frequencies that correspond to significant cyclic variation in a time series. Peaks in the periodogram reveal the dominant frequencies associated with cyclical components in an observed time series.
One topic that is crucial in time series analysis in the frequency domain is how often a time series should be sampled. Consider sampling the outdoor air temperature, for example, in Washington, DC. There are two significant cyclic components that should become apparent in such a time series. First, there is a daily temperature cycle. Temperatures are warmer during the day and cooler at night. This corresponds to high frequency variation. Second, there is an annual temperature cycle. Temperatures are warmer during the summer and cooler during the winter. This corresponds to low frequency variation. There is a factor of 365 (well, actually 365.24219) that separates the frequencies of these two cycles which should be accounted for in how often the time series is sampled. The following illustrations provide instances of sampling this time series too often, sampling this time series not often enough, and sampling this time series at about the right intervals to capture these two frequencies in a periodogram.
- Let's say you sample 1000 outdoor air temperatures at Reagan National Airport in Washington DC every second beginning at noon on July 20, 1969. This data collection will be over very soon because 1000 seconds is only about 17 minutes. But you have not covered a daily cycle or an annual cycle, so the frequencies for these two cycles cannot be detected from this sample. The sampling is too frequent.
- Let's say you sample 100 outdoor air temperatures at Reagan National Airport in Washington DC annually beginning at noon on July 20, 1969. This experiment will take you a long time to collect because the last value collected will be at noon on July 20, 2068. Even though you have collected the observations through 100 annual temperature cycles and tens of thousands of daily temperature cycles, neither the daily nor the annual cycle can be detected. All observations were made during the summer and during the day. The sampling was too infrequent.
- If you desire to detect both the daily and the annual outdoor air temperature cycles at Reagan National Airport, then a sampling interval between the two extremes (every second and every year from the previous two illustrations) must be used. So if you begin sampling hourly data at noon on July 20, 1969 and collect this data for three years, you will have collected outdoor temperature observations over three annual cycles and about a thousand daily cycles. This requires [latex]3 \cdot 365 \cdot 24 = 26,280[/latex] outdoor air temperatures to be collected. This time series allows an analyst to detect both daily and annual cycles. The periodogram, which estimates the spectral density function will have a peak associated with the low frequency (annual) cycles and a second peak associated with the high frequency (daily) cycles.
The details associated with computing the periodogram are left for a full-semester class in time series analysis. Some of the fundamental ideas will be presented here in order to give a sense of the development of the estimator. As has been the case in regression and survival analysis, we begin with a model for a time series having cyclic behavior. One such model is
where c is the amplitude of the cyclic variation, ω is the frequency of the cyclic variation, [latex]\phi[/latex] is a phase shift parameter, and the angle is measured in radians. (The [latex]\phi[/latex] used here has nothing to do with [latex]\phi[/latex] from the autoregressive time series models in the time domain.) Unfortunately, this model does not contain any random terms, and such a time series only occurs rarely in practice. So adding a time series of white noise [latex]\left\{ Z_t \right\}[/latex] results in the much more practical model
Since the phase shift parameter can be tedious in parameter estimation, it is common practice in spectral analysis to apply the trigonometric identity [latex]\cos(x + y) = \cos x \, \cos y - \sin x \, \sin y[/latex] to this model, which results in
where [latex]a = c \cdot \cos (\phi)[/latex] and [latex]b = -c \cdot \sin(\phi)[/latex]. This result is symmetric in the two primary trigonometric functions sine and cosine. The derivation thus far has only involved a single frequency ω. As in the previous outdoor air temperature example, it is often the case that there are multiple frequencies of interest. The current time series model can be generalized by summing over the k frequencies [latex]\omega_1, \, \omega_2, \, \ldots , \, \omega_k[/latex]:
where the amplitudes aj and bj reflect the contribution of frequency ωj to the variability of Xt. For example, if [latex]a_j = b_j = 0[/latex] for one particular index j, then the associated frequency ωj makes no contribution to the variability of Xt. The three remaining loose ends are (a) the number of frequencies k to consider, (b) which frequencies [latex]\omega_1, \, \omega_2, \, \ldots , \, \omega_k[/latex] to consider, and (c) how to estimate the amplitudes [latex]a_1, \, a_2, \, \ldots, \, a_k[/latex] and [latex]b_1, \, b_2, \, \ldots, \, b_k[/latex]. These loose ends are easier to navigate if the number of elements in the time series n happens to be even, which is assumed for now. If so, then the usual practice is to let [latex]k = n / 2[/latex] and space the ωj values uniformly between 0 and π as
The lowest frequency that can be detected by the periodogram is [latex]\omega_1 = 2 \pi / n[/latex] and the highest frequency that can be detected by the periodogram is [latex]\omega_{n/2} = \pi[/latex], the Nyquist frequency. The periodogram can be calculated in R with the spectrum function, which is available in the base language. Periodograms often contain significant sampling variability and do not provide a consistent estimator of the spectral density function, so time series analysts often use various techniques to smooth the raw periodogram values.
The previous example showed that the periodogram for the target MA(1) process, on average, appears to converge to the associated spectral density function. As illustrated in the final example, you will typically be working with just a single periodogram, which is typically quite noisy.
9.6 Exercises
-
9.1 For a stationary AR(1) model, find [latex]V\big[ \bar X \big][/latex]. Give an approximation for [latex]V\big[ \bar X \big][/latex] for large values of n.
-
9.2 Implement a Monte Carlo simulation that evaluates the method of moments, least squares, and maximum likelihood estimation techniques for an AR(1) model with [latex]n = 100[/latex] observed values and population parameters [latex]\phi = -3 / 4[/latex] and [latex]\sigma _ Z ^ {\, 2} = 1[/latex] and identify the technique that has the smallest mean square error for estimating [latex]\phi[/latex].
-
9.3 Consider a shifted AR(1) time series model with known parameter values μ, [latex]\phi[/latex], and [latex]\sigma _Z ^ {\, 2}[/latex]. One realization of the time series [latex]x_1, \, x_2, \, \ldots, \, x_{100}[/latex] has been observed. Perform Monte Carlo simulation experiments that provide convincing numerical evidence that the exact two-sided 95% prediction intervals for X101 and X102 are indeed exact prediction intervals for parameter settings of your choice.
-
9.4 Consider a stationary shifted AR(1) model defined by
where μ, [latex]-1 < \phi < 1[/latex], and [latex]\sigma _ Z ^ {\, 2} > 0[/latex] are fixed known parameters and Zt is Gaussian white noise. Find expressions for
- [latex]\displaystyle{ \lim_{h \, \rightarrow \, \infty} E \left[ X _ {n + h} \, | \, X_1 = x_1, \, X_2 = x_2 , \, \ldots , \, X_n = x_n \right] }[/latex]
- [latex]\displaystyle{ \lim_{h \, \rightarrow \, \infty} V \left[ X _ {n + h} \, | \, X_1 = x_1, \, X_2 = x_2 , \, \ldots , \, X_n = x_n \right]. }[/latex]
-
9.5 Find the limiting half-width of a exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]E \left[ \hat X_ {n + h} \right][/latex] as the time horizon [latex]h \rightarrow \infty[/latex] for an AR(1) time series model with all parameters known.
-
9.6 For a stationary shifted ARMA([latex]p, \, q[/latex]) time series model with population autocorrelation function [latex]\rho(k)[/latex], the population variance of the sample mean is
This result was proved in Section 8.2.1. Use this result to find an approximate 95% confidence interval for μ for the beaver data from Example 9.3 for a fitted shifted AR(1) time series model with Gaussian white noise error terms.
-
9.7 The built-in R time series lh consists of [latex]n = 48[/latex] observations of the luteinizing hormone in blood samples from a woman taken at 10 minute intervals.
- Plot the time series, the sample autocorrelation function and the sample partial autocorrelation function.
- Suggest an ARMA([latex]p, \, q[/latex]) model based on your plots.
- Make a scatter plot of the data pairs [latex](x_{t - 1}, \, x_t)[/latex].
- Compute the method of moments estimates of the parameters in the model suggested in part (b).
- Compute the maximum likelihood estimates of the parameters in the model suggested in part (b).
- Compute an approximate 95% confidence interval for [latex]\phi[/latex].
- Forecast the next three values in the time series and report 95% prediction intervals for the three forecasts.
- Perform some research on the luteinizing hormone and indicate some scientific evidence that the time series model you suggested in part (b) is plausible.
-
9.8 Report the test statistic and p-value for the turning point test applied to the time series of beaver temperatures in their active state from Example 9.3. Comment on the sign of the test statistic and the magnitude of the p-value.
-
9.9 Consider the time series of [latex]n = 70[/latex] consecutive yields from a batch chemical process (from Box, G.E.P., and Jenkins, G.M. (1976), Time Series Analysis: Forecasting and Control, Revised Edition, Holden–Day, page 32) given in Example 7.20.
- Plot the time series, the sample autocorrelation function and the sample partial autocorrelation function.
- Suggest an ARMA([latex]p, \, q[/latex]) model based on your plots.
- Make a scatter plot of the data pairs [latex](x_{t - 1}, \, x_t)[/latex].
- Compute the method of moments estimates of the parameters in the model suggested in part (b).
- Compute the maximum likelihood estimates of the parameters in the model suggested in part (b).
- Compute an approximate 95% confidence interval for [latex]\phi[/latex].
- Forecast the next three values in the time series and report 95% prediction intervals for the three forecasts.
-
9.10 Consider an AR(1) model with population parameters [latex]\phi = 0.8[/latex] and [latex]\sigma _ Z ^ {\, 2} = 1[/latex], and Gaussian white noise. Let [latex]r_1, \, r_2 , \, r_3[/latex] denote the sample autocorrelation function values of the residuals of the fitted time series associated with [latex]n = 100[/latex] observations. Use Monte Carlo simulation to estimate the population mean vector and population variance–covariance matrix, to one-digit accuracy, of [latex]r_1, \, r_2 , \, r_3[/latex] when maximum likelihood estimation is used to estimate the parameters.
-
9.11 Let B1 and B2 be the roots of the characteristic equation [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B ^ 2 = 0[/latex] for an AR(2) time series model
Let [latex]G_1 = B_1^{-1}[/latex] and [latex]G_2 = B_2^{-1}[/latex]. A general solution for the lag k autocorrelation is (see Box, G.E.P., and Jenkins, G.M. (1976), Time Series Analysis: Forecasting and Control, Revised Edition, Holden–Day, page 59)
for [latex]G_1 \ne G_2[/latex]. Show that calculating the population autocorrelation in this fashion is the same as using the recursive equation for the first five lags for an AR(2) process with parameters
- [latex]\phi_1 = 1 / 2[/latex], [latex]\phi_2 = 1 / 3[/latex],
- [latex]\phi_1 = 1[/latex], [latex]\phi_2 = -1 / 2[/latex].
-
9.12 Create a plot like the one in Figure 9.13 for an AR(2) model stationary region with [latex]\rho(1) = -0.9, \, -0.8, \, \ldots , \, 0.9[/latex] and [latex]\rho(2) = -0.9, \, -0.8, \, \ldots , \, 0.9[/latex]. No labels are necessary on your plot.
-
9.13 A stationary AR(2) time series model can be written as an MA(∞) time series model. The coefficients θ1, θ2, … in the MA(∞) model can be calculated in four fashions. First, they can be calculated using the recursive formulas in Theorem 9.12. Second, they can be written explicitly as (Cryer, J.D. and Chan, K–S, Time Series Analysis: With Applications in R, 2008, Springer, page 75):
for [latex]i = 1, \, 2, \, \ldots[/latex], where B1 and B2 are the roots of [latex]\phi(B) = 1 - \phi_1 B - \phi_2 B ^ 2[/latex], [latex]{G_1 = B_1^{-1}}[/latex], [latex]{G_2 = B_2^{-1}}[/latex], [latex]R = \sqrt{- \phi_2}[/latex], and [latex]\cos \Theta = \phi_1 / (2R)[/latex]. Third, the coefficients can be calculated by using the factored form of the characteristic polynomial, and writing the model in terms of Xt and equating coefficients. Fourth, the coefficients can be calculated by using the ARMAtoMA function in R. Calculate the first eight coefficients of the MA(∞) model, [latex]\theta_1, \, \theta_2, \, \ldots , \, \theta_8[/latex], using these four methods for the following sets of AR(2) parameters:
- [latex]\phi_1 = 1, \, \phi_2 = -1 / 4[/latex],
- [latex]\phi_1 = 1 / 2, \, \phi_2 = 1 / 9[/latex],
- [latex]\phi_1 = 1, \, \phi_2 = -1 / 2[/latex].
These three parameter combinations correspond to one real root with multiplicity two, two distinct real roots, and two complex roots of the characteristic equation [latex]\phi(B) = 0[/latex].
-
9.14 For an AR(2) time series model, the asymptotic variance–covariance matrix of the maximum likelihood estimates [latex]\hat \phi_1[/latex] and [latex]\hat \phi_2[/latex] is
What is the asymptotic population correlation between [latex]\hat \phi_1[/latex] and [latex]\hat \phi_2[/latex]?
-
9.15 Consider an AR(2) time series model with [latex]\phi_1 = 1[/latex], [latex]\phi_2 = -1 / 2[/latex], and [latex]\sigma _ Z ^ {\, 2} = 1[/latex]. For a realization of [latex]n = 100[/latex] observations [latex]X_1, \, X_2, \, \ldots, \, X_{100}[/latex] from this AR(2) model, give convincing numerical evidence that the forecasted value for X103 is unbiased and that the 95% prediction interval for X103 is exact.
-
9.16 Implement Theorem 9.17 on the R built-in LakeHuron time series to calculate the first five forecasted values and associated prediction intervals. Do not just use the predict function.
-
9.17 Consider a standard AR(2) model for an observed time series of [latex]n = 100[/latex] values. The last two values in the time series are [latex]x_{99} = 3[/latex] and [latex]x_{100} = 4[/latex]. The estimated coefficients in the AR(2) model are [latex]\hat \phi_1 = 1[/latex] and [latex]\hat \phi_2 = -0.5[/latex]. Compute the next ten forecasted values [latex]\hat X_{101}, \, \hat X_{102}, \, \ldots, \, \hat X_{110}[/latex] and comment on the shape of the forecasted values.
-
9.18 Consider a realization [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] of a stationary shifted AR(2) time series model with fixed known parameters μ, [latex]\phi_1[/latex], [latex]\phi_2[/latex], and [latex]\sigma _ Z ^ {\, 2}[/latex]. Write a formula for [latex]\hat X_{n+3}[/latex] in terms of [latex]x_{n - 1}[/latex] and xn.
-
9.19 Consider the annual Lake Huron water level heights from 1875 to 1972 given in the R built-in data set LakeHuron, appended by the next ten observations,
for the years 1973 to 1982. Give the p-value associated with a test of the statistical significance of the slope of the simple linear regression line for the augmented time series.
-
9.20 Consider the AR(3) model with coefficients
- Is this model invertible?
- Is this model stationary?
- Calculate the first six coefficients of the associated MA(∞) model.
-
9.21 Two necessary, but not sufficient, conditions for stationarity of an AR(p) time series model are (Cryer, J.D. and Chan, K–S, Time Series Analysis: With Applications in R, 2008, Springer, page 76):
- Show that these conditions hold for the stationary AR(4) time series model with
- Graphically or algebraically, show that these conditions are necessary but not sufficient for falling in the triangular-shaped stationary region from Theorem 9.9 for an AR(2) time series model.
-
9.22 Consider the AR(4) time series model with characteristic polynomial
and Gaussian white noise with population variance [latex]\sigma _ Z ^ {\, 2} = 1[/latex]. Conduct a Monte Carlo simulation experiment that provides convincing numerical evidence that [latex]\gamma(0) = 3520 / 819[/latex].
-
9.23 The R vector phi contains the parameters [latex]\phi_1, \, \phi_2, \, \ldots , \, \phi_p[/latex] in an AR(p) model. Write an R function named is.stationary with a single parameter phi that returns TRUE if the AR(p) model is stationary and FALSE otherwise.
-
9.24 The R code below takes initial p autocovariances [latex]\gamma(0), \, \gamma(1), \, \ldots , \, \gamma(p - 1)[/latex] for an AR(p) model, which are stored in the vector gam, and places them in a variance–covariance matrix GAMMA (denoted by Γ in the text).
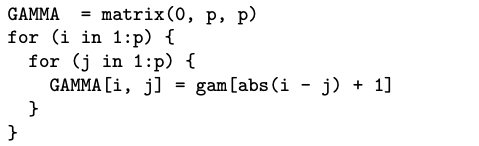
The code makes this conversion by using two nested for loops. Heather can do this calculation without using for loops. How does she do it?
-
9.25 Consider a time series that is governed by an AR(4) model with characteristic polynomial
and Gaussian white noise with population variance [latex]\sigma _ Z ^ {\, 2} = 1[/latex]. Conduct a Monte Carlo simulation experiment that provides convincing numerical evidence that the 95% confidence interval for [latex]\phi_3[/latex] based on the maximum likelihood estimators for an AR(4) time series model is asymptotically exact.
-
9.26 For logarithms of the [latex]n = 55[/latex] annual lynx pelt sales time series from Example 9.29, find the values of p and q associated with the ARMA(p, q) model that minimizes the AIC statistic. Assume that the models are fitted by maximum likelihood.
-
9.27 Fit the AR(4) model to the logarithms of the [latex]n = 55[/latex] annual lynx pelt sales time series from Example 9.29 by maximum likelihood. Simulate the fitted model to generate [latex]n = 55[/latex] random annual lynx pelt sales from the fitted model. View a dozen or so such realizations and comment on your faith in the fitted AR(4) time series model. Repeat the experiment for a fitted ARMA(2, 3) time series model and comment.
-
9.28 Show that the MA(1) model
and the MA(1) model
have the same population autocorrelation function.
-
9.29 Show that [latex]-1/2 \le \rho(1) \le 1/2[/latex] for an MA(1) model.
-
9.30 Derive the population autocorrelation function for the MA(1) model with arbitrary mean value μ given by
in a similar fashion to the derivation for the standard MA(1) model.
-
9.31 Conduct the following Monte Carlo simulation experiment. Generate [latex]n = 100[/latex] observations from an MA(1) time series model with [latex]\theta = 0.9[/latex] and standard normal white noise terms. Estimate the expected value and standard deviation of r1 and r2. Run enough replications to that you can report your estimates to two significant digits.
-
9.32 Consider an MA(1) model with [latex]\theta = -0.9[/latex] and Gaussian white noise with [latex]\sigma _ Z ^ {\, 2} = 1[/latex]. Generate a dozen realizations of this time series for [latex]n = 100[/latex] observations each. Plot the time series and the associated correlogram, using a call to Sys.sleep between each realization to view the graphs. Write a paragraph that describes what you observe in the dozen realizations.
-
9.33 Consider an MA(1) time series model
where [latex]\left\{ Z_t \right\}[/latex] denotes Gaussian white noise. Let [latex]\hat \theta _ {\scriptscriptstyle{MOM}}[/latex] be the method of moments estimator of θ and let [latex]\hat \theta _ {\scriptscriptstyle{MLE}}[/latex] be the maximum likelihood estimator of θ. One way to compare these two estimators is the asymptotic relative efficiency, defined as
Brockwell and Davis (2016, page 129) give the population variance of [latex]\hat \theta _ {\scriptscriptstyle{MOM}}[/latex] and [latex]\hat \theta _ {\scriptscriptstyle{MLE}}[/latex] as approximately
Write a Monte Carlo simulation that confirms these two formulas for [latex]n = 400[/latex], [latex]\theta = 1 / 2[/latex], and [latex]\sigma _ Z ^ {\, 2} = 1[/latex].
-
9.34 The [latex]n = 45[/latex] daily average number of defects per truck at the final inspection at a manufacturing facility (from Burr, 1976, Statistical Quality Control Methods, Marcel Dekker, New York), read row-wise, are given below.
1.20
1.50
1.54
2.70
1.95
2.40
3.44
2.83
1.76
2.00
2.09
1.89
1.80
1.25
1.58
2.25
2.50
2.05
1.46
1.54
1.42
1.57
1.40
1.51
1.08
1.27
1.18
1.39
1.42
2.08
1.85
1.82
2.07
2.32
1.23
2.91
1.77
1.61
1.25
1.15
1.37
1.79
1.68
1.78
1.84
Fit these data values to a shifted MA(1) time series model by the method of moments, least squares, and maximum likelihood estimation.
-
9.35 The formula for the population variance of the sample mean for a stationary time series model (which was proved in Section 8.2.1) is
Show that this is approximately
or, equivalently,
for large values of n whenever the autocorrelation function values decay rapidly enough with increasing k such that

