Chapter 3 Topics in Regression
The previous two chapters have provided a detailed introduction to the basic principles underlying simple linear regression. This chapter will cover some additional topics in regression, but not with the same detail as in the previous two chapters. Sometimes just a single example will illustrate a regression topic that deserves an entire chapter in a full-semester regression course. The topics considered in this chapter are forcing a regression line through the origin, diagnostics, remedial procedures, the matrix approach to simple linear regression, multiple linear regression, weighted least squares estimators, regression models with nonlinear terms, and logistic regression.
3.1 Regression Through the Origin
Applications occasionally arise in which it is of benefit to force a regression line to pass through the origin. To illustrate such applications, return to Examples 1.1 and 1.3 in which Bob and Cheryl each had the number of sales per week as an independent variable X. In both of the examples, [latex]X = 0[/latex] sales per week corresponds to [latex]Y = 0[/latex] commissions (for Bob) and [latex]Y = 0[/latex] revenue per week (from Cheryl's sales). In these settings it is sensible to force the regression line to pass through the origin; estimating a population intercept does not make sense. The resulting regression model does not contain the β0 parameter. The simple linear regression model forced through the origin, sometimes abbreviated RTO for regression through the origin, is defined next.
The regression parameter β1 can be estimated using least squares from the data pairs [latex](X_i, \, Y_i)[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
The next example conducts a hypothesis test to determine whether it is appropriate to drop the intercept term from the simple linear regression model based on the data pairs, and then proceeds to fit the reduced model.
The next example revisits the regression modeling of the stopping distance as a function of the speed of a car in the built-in cars data frame.
This ends the discussion of forcing the regression line through the origin. Occasions arise in regression modeling in which it is more appropriate to fit a statistical model with fewer parameters. Some of the results from the full simple linear regression model generalize to simple linear regression forced through the origin. The point estimate for β1, for example, is unbiased. Three examples of results that do not generalize are (a) the residuals do not necessarily sum to zero, (b) the regression line does not necessarily pass through the point [latex]\big( \bar X, \, \bar Y \big)[/latex], and (c) it is possible that SSE can exceed the total sum of squares SST, which can result in a negative value of R2.
3.2 Diagnostics
Diagnostic procedures are applied to fitted regression models to assess their conformity to the assumptions (for example, constant variance of the error terms) implicit in the simple linear regression model. We have already considered one such diagnostic procedure from the previous chapter, which is the examination of the residuals to assess their independence, constant variance, and normality. Two other diagnostic procedures will be examined here, which are the identification of data pairs known as leverage points and the identification of data pairs known as influential points. The subsequent section considers remedial procedures, which can be applied to a regression model that fails to satisfy one or more of the assumptions implicit in a regression model.
3.2.1 Leverage
Data pairs that have the ability to exert more influence on the regression line than other data pairs due to their independent variable values are known as leverage points. These data pairs should be given more scrutiny than the others because of the potential tug that they have on the regression line. More specifically, when the value of the independent variable is unusually far from [latex]\bar {X}[/latex] (either low or high), the data pair has the potential to exert more pull on the regression line than other points.
We begin developing the notion of leverage by expressing the predicted value of Yi, denoted by [latex]\hat{Y}_i[/latex], as a function of Yi. Using Theorems 1.1 and 1.3, the predicted value of Yi is
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The [latex]h_{ij}[/latex] values form the elements of an [latex]n \times n[/latex] matrix [latex]{\bf H}[/latex], which is often referred to as the hat matrix or the projection matrix. The reason that this matrix is known as the projection matrix is that it provides a linear transformation from the observed values of the dependent variable to the associated fitted values. The diagonal elements of the hat matrix are known as the leverages of the data pairs, which are defined next.
The leverage is a measure of a data pair's potential to influence the regression line. Notice that the leverage is a function of the values of the independent variable [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] only; the heights of the data pairs do not play a role. Since the two denominators in the expression from Definition 3.2 are constants for a particular data set, only the numerator [latex]\left( X_i - \bar X \right) ^ 2[/latex] changes for each value of Xi. It reflects the distance between a particular Xi value and its associated sample mean. The leverage increases as the distance between Xi and [latex]\bar X[/latex] increases. There are several results concerning the leverages; one that concerns the average of the leverages is presented next.
To summarize what we know about the n leverages,
- the leverages are the diagonal elements of the hat matrix H,
- all leverages are positive, with a minimum of [latex]1 / n[/latex] (for [latex]X_i = \bar X[/latex]) and a maximum of 1, and
- the sum of the leverages is 2, so the average of the leverages is [latex]2 / n[/latex].
If all of the leverages are equal (this is always the case, for example, for [latex]n = 2[/latex] data pairs), then each leverage is [latex]2 / n[/latex], which is the average from Theorem 3.2. We would like to establish a threshold at which a data pair has the ability to exert a significant influence over the regression line so that such points might be examined with additional scrutiny. Such data pairs are known as leverage points. Although not used universally, a common way to identify a leverage point is if the leverage [latex]h_{ii}[/latex] is more than twice the average of the leverages. Symbolically, a point is designated a leverage point if
This threshold will be illustrated in the next example.
The previous example has indicated a fitted simple linear regression model is likely to pass close to a leverage point. Leverage points exert more tug on the regression line than those points whose independent variable value is closer to [latex]\bar X[/latex]. The next illustration of identifying leverage points revisits the heights of couples from Example 2.7.
Identifying leverage points is helpful for knowing which points to more carefully scrutinize. It is not appropriate to simply delete a leverage point because it falls far from the regression line. Leverage points can be helpful in highlighting an aspect of the model that was not originally considered relevant. The next subsection considers how to determine if a leverage point (or any other point) does produce a significant impact on [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex].
3.2.2 Influential Points
Leverage points have the potential to produce large changes in the values of [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex] when they are deleted. How can we determine whether a leverage point (or any other point) does have significant impact on the regression line? American statistician R. Dennis Cook suggested a quantity that measures the influence of each data pair on the regression line.
The equivalence between the three very diverse formulas in Definition 3.3 is left as an exercise. The data pairs must not be collinear because MSE appears in the denominator of each formula. Each of the three formulas is helpful in developing intuition about Cook's distance, so each is illustrated in the following three examples.
The previous example has indicated that Cook's distance is a measure of the influence of each data pair based on the effect of removing each data pair sequentially, and measuring the associated impact on the fitted values. If the fitted values are not substantially altered by removing data pair i, then Di will be small; if the fitted values are substantially altered by removing data pair i, then Di will be large. This, however, does not explain why the denominator [latex]2 \cdot MSE[/latex] is in all four formulas in Definition 3.3. That will be addressed in the next example.
One weakness associated with the first two formulas for computing the Cook's distances in Definition 3.3 involves computation time. There are [latex]n + 1[/latex] regression lines to estimate (one for all of the data pairs and then another n associated with dropping each of the data pairs). For large values of n, this can require significant computation time. The third formula is much faster, as illustrated next.
Cook's distances are effective for identifying influential points. Once an influential point in a simple linear regression model has been identified, there are several possible next steps.
- The influential point might have been recorded or coded improperly; a typographical error has occurred. In most situations, this is easily remedied.
- The influential point has some unusual characteristic that is not present with the other data points that might account for it being deemed influential. Depending on the setting, the influential point can be removed and the regression model can be refitted without the influential point.
- The influential point might provide some evidence that an alternative regression model is appropriate. This might be a nonlinear regression model or a linear regression model with additional independent variables.
- The influential point might be at one of the extremes of the scope of the model. This might indicate that the scope of the model is too wide; narrowing the scope should be considered. It is often the case that a simple linear regression model is valid only over a rather limited scope. This might result in eliminating all data points outside of the narrowed scope and refitting the simple linear regression model.
- The high-leverage point is indeed within the scope of the model and was recorded correctly, but its extreme influence on the regression line is resulting in poor diagnostic measures. One approach here is to collect more data values, particularly at the extreme values of the independent variable within the scope of the model in order to mitigate the effect of the influential point.
3.3 Remedial Procedures
The diagnostic procedures presented in the previous section are designed to identify assumptions associated with the simple linear regression model that are not satisfied for a particular set of n data pairs. But these diagnostic procedures do not suggest remedies when model assumptions are not satisfied. This section considers remedial procedures.
Reasons that simple linear regression model with normal error terms can fail to satisfy the assumptions given in Definition 2.1 include
- the regression function is not linear,
- the regression model has not included an important independent variable,
- the error terms have a variance that varies with X,
- the error terms are not independent,
- the error terms are not normally distributed,
- the scope of the regression model is too wide,
- the scope of the regression model is too narrow, and
- an influential point has an unusually strong effect on the regression line.
Two common approaches to handling a regression model which violates one or more of the assumptions are (a) formulate and fit a regression model with nonlinear terms, and (b) transform the X-values or the Y-values (or both) in a fashion so that the simple linear regression assumptions are satisfied. Regression models with nonlinear terms will be considered in a subsequent section in this chapter; transformations will be considered here. Transformations will be illustrated in a single (long) example.
The previous example took a trial-and-error approach to determining an appropriate transformation to apply to the raw data pairs in order to satisfy the assumptions implicit in a simple linear regression model with normal error terms. There are templates that can give a more systematic approach to determining these transformations.
There is a nice synergy between matrix algebra and regression, which will be presented in the next section.
3.4 Matrix Approach to Simple Linear Regression
So far, a purely algebraic approach has been taken to simple linear regression modeling. This section considers a matrix-based approach. There are (at least) four reasons to take this approach. First, the mathematical expressions are in many cases much more compact; summations from the algebraic approach are often equivalent to matrix multiplications. Second, matrix algebra can easily be implemented on a computer. Third, the matrix approach generalizes very easily to the multiple regression case in which there are several independent variables. Fourth, the matrix approach generalizes very easily to weighted least squares, which will be introduced in the next section.
We begin the matrix approach by defining certain critical matrices, which will be set in boldface. Let [latex]{\bf X}[/latex] be an [latex]n \times 2[/latex] matrix whose first column is all ones and whose second column contains the observed values of the independent variable, [latex]{\bf Y}[/latex] be an [latex]n \times 1[/latex] vector which holds the observed values of the dependent variable, [latex]\pmb{\beta}[/latex] be a [latex]2 \times 1[/latex] vector which holds the population intercept and slope, and [latex]\pmb{\epsilon}[/latex] be an [latex]n \times 1[/latex] vector which holds the error terms:
The [latex]\bf X[/latex] matrix is known as the design matrix.
As before, the values of the independent variable (the second column of [latex]\bf X[/latex]) are assumed to be fixed constants observed without error with at least two distinct values, the values of the dependent variable contained in [latex]\bf Y[/latex] are assumed to be continuous random responses, and the elements of the vector [latex]\pmb\epsilon[/latex] are assumed to be mutually independent random variables, each with population mean 0 and finite positive population variance σ2. Stated another way, the expected value of [latex]\pmb\epsilon[/latex] is the zero vector and the variance–covariance matrix of [latex]\pmb\epsilon[/latex] is
The simple linear regression model
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], can be written more explicitly in terms of each observed data pair as
which, in matrix form, is
or simply
This explains why the artificial column of ones appears as the first column of the [latex]{\bf X}[/latex] matrix; it is to account for the intercept term. To force a regression line through the origin, simply omit the column of ones in the [latex]{\bf X}[/latex] matrix. Taking the expected value of both sides of this equation results in
because [latex]E[ \epsilon_i ] = 0[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], (that is, [latex]E[ \pmb{\epsilon} ] = {\bf 0}[/latex]). The left-hand side of this equation, [latex]E[ {\bf Y} ][/latex], is an n-element column vector with elements [latex]E[Y_1], \, E[Y_2], \ldots , \, E[Y_n][/latex]. The sum of squares which is to be minimized to find the least squares estimators is
With this notation established, the algebraic results concerning the simple linear regression model can be restated more compactly in terms of these matrices. The results have already been proved, so there is no need to prove them again when stated in matrix form. The [latex]\, ^ \prime[/latex] superscript denotes transpose. It is a good exercise to perform the algebra necessary to see that the algebraic and matrix versions of these definitions and theorems match. The dimensions of the matrices should be checked for conformity.
- Definition 1.1. The simple linear regression model is
where [latex]E[ \pmb{\epsilon} ] = {\bf 0}[/latex], [latex]V[ \pmb{\epsilon} ] = \sigma ^ {\, 2} {\bf I}[/latex], and [latex]{\bf I}[/latex] is the [latex]n \times n[/latex] identity matrix.
- Theorem 1.1. The least squares estimators of [latex]\pmb{\beta}[/latex], denoted by [latex]\hat{\pmb{\beta}} = \big( \hat \beta_0 , \, \hat \beta_1 \big) ^ \prime[/latex], solve the normal equations
The [latex]{\bf X}[/latex] matrix has rank 2 because there are at least two distinct Xi values. So [latex]{\bf X} ^ \prime {\bf X}[/latex] is invertible and the normal equations have the unique solution
by premultiplying both sides of the normal equations by [latex]\big( {\bf X} ^ \prime {\bf X} \big) ^ {-1}[/latex].
- Theorem 1.2. The least squares estimator of [latex]\pmb{\beta}[/latex] in a simple linear regression model is an unbiased estimator of [latex]\pmb{\beta}[/latex] because
- Theorem 1.3. The least squares estimators of [latex]\pmb{\beta}[/latex] in the simple linear regression model can be written as linear combinations of the dependent variables:
where the coefficients in the linear combinations are given by [latex]\big( {\bf X} ^ \prime {\bf X} \big) ^ {-1} {\bf X} ^ \prime[/latex].
- Theorem 1.4. The variance–covariance matrix of the least squares estimators of [latex]\pmb{\beta}[/latex] is
- Theorem 1.5 (Gauss–Markov theorem). The least squares estimators of [latex]\pmb{\beta}[/latex] in a simple linear regression model, [latex]\hat{\pmb{\beta}} = ( {\bf X} ^ \prime {\bf X} ) ^ {-1} {\bf X} ^ \prime {\bf Y}[/latex], have the smallest population variance amongst all linear unbiased estimators of [latex]\pmb{\beta}[/latex].
- Definition 1.2. The vector of fitted values in a simple linear regression model is the [latex]n \times 1[/latex] column vector
which is a linear combination of the dependent variables. The vector of residuals is the [latex]n \times 1[/latex] column vector
which is also a linear combination of the dependent variables. The matrix [latex]{\bf I}[/latex] is the [latex]n \times n[/latex] identity matrix.
- Theorem 1.6. For the simple linear regression model with fitted values [latex]\bf\hat{Y}[/latex] and residuals [latex]{\bf e}[/latex],
- [latex]{\bf e} ^ \prime {\bf 1} = 0[/latex],
- [latex]{\bf Y} ^ \prime {\bf 1} = \bf\hat{Y}^ {\kern 0.19em \prime} {\bf 1}[/latex]
- [latex]\bf\hat{Y}^ {\kern 0.19em \prime} {\bf e} = 0[/latex],
where [latex]{\bf 1}[/latex] is an n-element column vector of ones.
- Theorem 1.7. An unbiased estimator of σ2 in a simple linear regression model is
- Theorem 1.8. The sums of squares can be partitioned in a simple linear regression model as [latex]SST = SSR + SSE[/latex] or
where [latex]\bar {\bf Y}[/latex] is an n-element column vector with identical elements which are each the sample mean of the values of the dependent variable.
- Definition 1.3. The coefficient of determination in a simple linear regression model is
when [latex]\big( {\bf Y} - \bar {\bf Y} \big) ^ \prime \big( {\bf Y} - \bar {\bf Y} \big) \ne 0[/latex]. The coefficient of correlation is
where the sign associated with r is positive when [latex]\hat \beta_1 \ge 0[/latex] and negative when [latex]\hat \beta_1 < 0[/latex].
- Definition 2.1. The simple linear regression model with normal error terms is
where [latex]\pmb{\epsilon} \sim N\left( {\bf 0}, \, \sigma ^ {\, 2} {\bf I} \right)[/latex].
- Theorem 2.1. For the simple linear regression model with normal error terms, the maximum likelihood estimators of [latex]\pmb{\beta}[/latex] are
and the maximum likelihood estimator of σ2 is
Since the vector of error terms [latex]\pmb{\epsilon}[/latex] consists of independent and identically distributed normal random variables, [latex]{\bf Y} = {\bf X} \pmb{\beta} + \pmb{\epsilon}[/latex] is a vector of independent and identically distributed normal random variables, and the linear transformation [latex]\hat{\pmb{\beta}} = ( {\bf X} ^ \prime {\bf X} ) ^ {-1} {\bf X} ^ \prime {\bf Y}[/latex] has normally distributed elements.
- Theorem 2.2. For the simple linear regression model with normal error terms,
and is independent of [latex]\hat{\pmb{\beta}}[/latex].
- Theorem 2.3. For the simple linear regression model with normal error terms, an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for σ2 is
- Theorems 2.4 and 2.7. For the simple linear regression model with normal error terms,
- Theorem 2.12. For the simple linear regression model with normal error terms, an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for [latex]E[ Y_h ][/latex] for a given value of the independent variable Xh is
where [latex]{\bf X}_h = (1, \, X_h) ^ \prime[/latex] and [latex]\hat{\sigma} ^ 2 = MSE[/latex].
- Theorem 2.15. For the simple linear regression model with normal error terms, an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]Y_h^\star[/latex] for a given value of the independent variable Xh is
where [latex]{\bf X}_h = (1, \, X_h) ^ \prime[/latex] and [latex]\hat{\sigma} ^ 2 = MSE[/latex].
- Theorem 2.16. Under the simple linear regression model with normal error terms and parameters estimated from the data pairs [latex]\left( X_1, \, Y_1 \right), \, \left( X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex],
- Theorem 2.17. Under the simple linear regression model with normal error terms and parameters estimated from the data pairs [latex]\left( X_1, \, Y_1 \right), \, \left( X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex], the values of β0 and β1 satisfying
form an exact joint [latex]{100(1 - \alpha)}\%[/latex] confidence region for β0 and β1.
- Definition 3.2. Under the simple linear regression model, the hat matrix is
The diagonal elements of the hat matrix are the leverages. The matrix equation
indicates that [latex]{\bf H}[/latex] transforms [latex]{\bf Y}[/latex] to [latex]\bf\hat{Y}[/latex]. The hat matrix is symmetric (that is, [latex]{\bf H} = {\bf H} ^ \prime[/latex]) and idempotent (that is, [latex]{\bf H} {\bf H} = {\bf H}[/latex]).
The matrix approach applied to a simple linear regression model is illustrated for a small sample size next.
Theorem 2.2 stated that under the simple linear regression model with normal errors,
An outline of the proof of Theorem 2.2 was given in Chapter 2 in purely algebraic terms. An outline of the proof to the result using the matrix approach to simple linear regression is given here to contrast the difference between the two approaches.
The matrix approach gives an alternative way of computing measures of interest in a simple linear regression. Using matrices also allows the following two helpful extensions to simple linear regression.
- Removing the first column of the [latex]{\bf X}[/latex] matrix that consists entirely of ones corresponds to forcing a regression line through the origin.
- Adding additional columns to the [latex]{\bf X}[/latex] matrix corresponds to including additional independent variables to the regression model, which is known as multiple linear regression. This is the topic of the next section.
3.5 Multiple Linear Regression
Multiple linear regression can often be applied when there are several independent variables (or predictors) [latex]X_1, \, X_2, \, \ldots, \, X_p[/latex] which can be used to explain a continuous dependent (or response) variable Y. Three examples are listed below.
- The asking price of a home Y is a function of
- the number of square feet in the home,
- the number of bedrooms, and
- acreage of the land associated with the home.
- The annual amount of money a person donates to charity Y is a function of
- the nationality of the person,
- the annual income of the person,
- the net worth of the person,
- the religious affiliation of the person,
- the age of the person, and
- the gender of the person.
- The stopping distance of a car Y is a function of
- the speed of the car,
- the weight of the car, and
- the type of brakes installed on the car.
One way to formulate a multiple linear regression model is to treat the left-hand side of the model as an expected value:
Since [latex]E[Y][/latex] denotes a conditional expectation of Y given the values of the p independent variables [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex], a more careful way to write this model is
So far, there has been no consideration of the probability distribution of the error terms, and that is addressed in the formal definition of a multiple linear regression model given next.
To estimate the parameters in a multiple linear regression model, we collect n observations which each consist of the p independent variables and the associated dependent variable. In most applications, [latex]p > n[/latex]. Occasions arise (often in biostatistical applications) in which [latex]p > n[/latex]. The formulation of the simple linear regression model with notation included for the n observations is
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. So [latex]X_{ij}[/latex] denotes the value of the jth independent variable collected on the ith observational unit. In the real estate example given at the beginning of this section, X83 is the value of the third independent variable (acreage) collected on the 8th home collected by the analyst. The associated asking price of the 8th home is Y8.
Figure 3.15 shows a portion of the population regression plane [latex]E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2[/latex] for a multiple linear regression model with [latex]p = 2[/latex] independent variables X1 and X2. The plane extends outward from the portion shown in Figure 3.15. The regression parameters β0, β1, and β2 are fixed constants. The intercept β0 is positive in Figure 3.15 because the plane strikes the Y-axis above the origin. Based on the inclination of the population regression plane relative to the X1- and X2-axes it is clear that [latex]\beta_1 < 0[/latex] and [latex]\beta_2 > 0[/latex]. To avoid clutter and highlight the geometry and notation, only the ith data triple [latex](X_{i1}, \, X_{i2}, \, Y_i)[/latex] and the associated error term ϵi are shown in the figure.
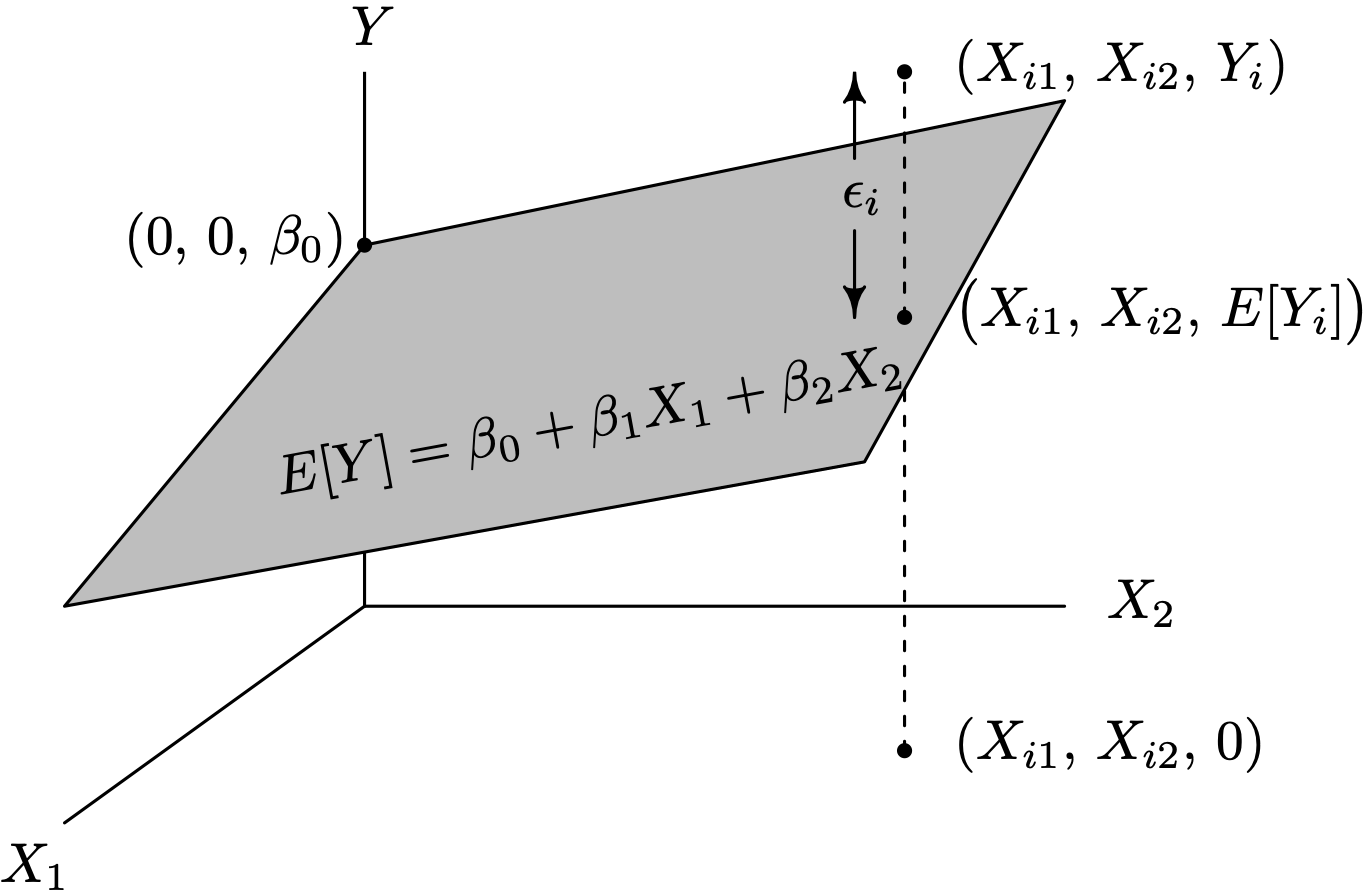
Long Description for Figure 3.15
A rectangular plane is plotted on the three-dimensional coordinate plane, labeled X 1, X2 and Y. The top left vertex of the rectangular plane falls on the Y axis with points 0, 0, beta subscript 0. Three collinear points,( X i 1, X i 2 and Y i); (X I 1, X I 2, E of Y I) in the X 2 Y plane and (X I 1, X I 2, 0) in the X 2, X 1 plane are connected by a dotted line. The point ( X I 1, X I 2, E of Y i) falls on the right end of the rectangular plane. The distance from (X i 1, X i 2, Y i) to( X i 1, X i 2, E of Y i )is indicated as E i. An equation within the rectangular plane reads, E of Y equals beta 0 plus beta 1 X 1 plus beta 2 X 2.
Figure 3.16 shows a portion of the estimated regression plane [latex]Y = \hat \beta_0 + \hat \beta_1 X_1 + \hat \beta_2 X_2[/latex] for a multiple linear regression model with [latex]p = 2[/latex] independent variables X1 and X2. The estimated regression parameters [latex]\hat \beta_0[/latex], [latex]\hat \beta_1[/latex], and [latex]\hat \beta_2[/latex] are random variables which are estimated from n data triples [latex]\left( X_{11}, \, X_{12} , \, Y_1 \right), \, \left( X_{21}, \, X_{22}, \, Y_2 \right), \, \ldots , \, \left( X_{n1}, \, X_{n2}, \, Y_n \right)[/latex]. The estimated regression parameters are random variables because the dependent variable values [latex]Y_1, \, Y_2, \, \ldots, \, Y_n[/latex] are random variables. The estimated intercept [latex]\hat \beta_0[/latex] is positive in Figure 3.16 because the plane strikes the Y-axis above the origin. Based on the inclination of the estimated regression plane relative to the X1- and X2-axes it is clear that [latex]\hat \beta_1 < 0[/latex] and [latex]\hat \beta_2 > 0[/latex]. To avoid clutter and highlight the geometry and notation, just the ith data triple [latex](X_{i1}, \, X_{i2}, \, Y_i)[/latex], the associated fitted value [latex](X_{i1}, \, X_{i2}, \, \hat{Y}_i)[/latex], and the associated residual ei are shown in the figure.

Long Description for Figure 3.16
A rectangular plane is plotted on the three-dimensional coordinate plane, labeled X 1, X 2 and Y. The top left vertex of the rectangular plane falls on the Y axis with points 0, 0, beta cap 0. Three collinear points, X i 1, X i 2 and Y i; X i 1, X i 2, Y cap i in the X 2 Y plane and X i 1, X i 2, 0 in the X 2, X 1 plane are connected by a dotted line. The point X i 1, X i 2, Y cap i falls on the right end of the rectangular plane. The distance from X i 1, X i 2, Y i to X i 1, X I 2, Y cap i is indicated as e i. An equation within the rectangular plane reads, Y equals beta cap 0 plus beta 1 X 1 plus bet 2 X 2.
When there are [latex]p > 2[/latex] independent variables, the estimated regression model is a hyperplane in [latex]{\cal R} ^ {p + 1}[/latex]. Residual i is the distance [latex]e_i = Y_i - \hat Y_i[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
When the error terms are assumed to be normally distributed, this model is known as the multiple linear regression model with normal error terms. This additional assumption allows for statistical inference concerning parameters and predicted values in a similar manner to that described in Chapter 2.
The multiple linear regression model can also be expressed in terms of matrices. Relative to the simple linear regression model, additional columns are appended to the [latex]{\bf X}[/latex] matrix, and the [latex]\pmb{\beta}[/latex] vector is expanded to include the parameters associated with the additional parameters:
The vectors [latex]{\bf Y}[/latex] and [latex]\pmb{\epsilon}[/latex] remain unchanged from the simple linear regression formulation. The first row of [latex]{\bf X}[/latex] corresponds to the values of the independent variables collected on the first observational unit, the second row of [latex]{\bf X}[/latex] corresponds to the values of the independent variables collected on the second observational unit, etc. As was the case in simple linear regression, [latex]{\bf X}[/latex] is known as the design matrix.
The good news about the matrix approach to multiple linear regression is that the definitions and results from simple linear regression only require some minor tweaking in order to generalize to multiple regression. Several of these definitions and results are given below. In many cases, it is just a matter of replacing the word “simple” with the word “multiple” or updating the degrees of freedom to account for the p independent variables. It is assumed that the [latex]{\bf X}[/latex] matrix has rank [latex]p + 1[/latex] (that is, a full rank matrix), which means that the columns of [latex]{\bf X}[/latex] are linearly independent.
- The multiple linear regression model is
where [latex]E[ \pmb{\epsilon} ] = {\bf 0}[/latex], [latex]V[ \pmb{\epsilon} ] = \sigma ^ {\, 2} {\bf I}[/latex], and [latex]{\bf I}[/latex] is the [latex]n \times n[/latex] identity matrix.
- The least squares estimators of [latex]\pmb{\beta}[/latex], denoted by [latex]\hat{\pmb{\beta}} = \big( \hat \beta_0 , \, \hat \beta_1 , \, \ldots , \, \hat \beta_p \big) ^ \prime[/latex], solve the normal equations
Since [latex]{\bf X}[/latex] has full rank, [latex]{\bf X} ^ \prime {\bf X}[/latex] is invertible and the normal equations have the unique solution
by premultiplying both sides of the normal equations by [latex]\big( {\bf X} ^ \prime {\bf X} \big) ^ {-1}[/latex].
- The least squares estimator of [latex]\pmb{\beta}[/latex] in a multiple linear regression model is an unbiased estimator of [latex]\pmb{\beta}[/latex] because
- The least squares estimators of [latex]\pmb{\beta}[/latex] in the multiple linear regression model can be written as linear combinations of the dependent variables:
where the coefficients in the linear combinations are given by [latex]\big( {\bf X} ^ \prime {\bf X} \big) ^ {-1} {\bf X} ^ \prime[/latex].
- The variance–covariance matrix of the least squares estimators of [latex]\pmb{\beta}[/latex] is
- (Gauss–Markov theorem) The least squares estimators of [latex]\pmb{\beta}[/latex] in a multiple linear regression model, [latex]\hat{\pmb{\beta}} = ( {\bf X} ^ \prime {\bf X} ) ^ {-1}{\bf X} ^ \prime {\bf Y}[/latex], have the smallest population variance amongst all linear unbiased estimators of [latex]\pmb{\beta}[/latex].
- The vector of fitted values in a multiple linear regression model is the [latex]n \times 1[/latex] column vector
which is a linear combination of the dependent variables. The vector of residuals is the [latex]n \times 1[/latex] column vector
which is also a linear combination of the dependent variables. The matrix [latex]{\bf I}[/latex] is the [latex]n \times n[/latex] identity matrix.
- The multiple linear regression model with normal error terms is
where [latex]\pmb{\epsilon} \sim N\left( {\bf 0}, \, \sigma ^ {\, 2} {\bf I} \right)[/latex].
- For the multiple linear regression model with normal error terms, the maximum likelihood estimators of [latex]\pmb{\beta}[/latex] are
and the maximum likelihood estimator of σ2 is
Since the vector of error terms [latex]\pmb{\epsilon}[/latex] consists of independent and identically distributed normal random variables, [latex]{\bf Y} = {\bf X} \pmb{\beta} + \pmb{\epsilon}[/latex] is a vector of independent and identically distributed normal random variables. Since [latex]\hat{\pmb{\beta}}[/latex] is a linear transformation of Y, [latex]\hat{\pmb{\beta}} \sim N \left( {\pmb{\beta}}, \, \sigma ^ {\, 2} \big( {\bf X} ^ \prime {\bf X} \big) ^ {-1} \right)[/latex].
- Under the multiple linear regression model, the [latex]n \times n[/latex] hat matrix is
The diagonal elements of the hat matrix are the leverages. The matrix equation
indicates that [latex]{\bf H}[/latex] transforms [latex]{\bf Y}[/latex] to [latex]\bf\hat{Y}[/latex]. The hat matrix is symmetric (that is, [latex]{\bf H} = {\bf H} ^ \prime[/latex]) and idempotent (that is, [latex]{\bf H} {\bf H} = {\bf H}[/latex]). The trace of the hat matrix is [latex]\sum_{i\,=\,1}^n h_{ii} = p + 1[/latex].
The example of multiple linear regression that follows considers [latex]p = 2[/latex] predictors of the sales price of a home.
A multiple linear regression model can easily be adapted to include nonlinear terms. A multiple regression model with two independent variables X1 and X2, for example, with a linear relationship between X1 and Y and a quadratic relationship between X2 and Y which includes an intercept term is
Using the R lm function to estimate the coefficients will be illustrated in Section 3.7.
Multiple linear regression has many more modeling issues that arise than simple linear regression. The subsections that follow consider the following topics within multiple regression: (a) handling categorical independent variables which fall in categories rather than quantitative values, (b) handling the case in which independent variables have interactive effects, (c) extending the ANOVA table to multiple independent variables, (d) calculation of the coefficient of determination for multiple linear regression, and an adjustment that can be made to reduce its bias, (e) the effect of multicollinearity among the independent variables, and (f) algorithms for model selection.
3.5.1 Categorical Independent Variables
Some regression models include independent variables which are not naturally quantitative, but are rather categorical. These categorical independent variables require some special treatment in order to be included in a multiple linear regression model. The cases in which a categorical independent variable falls in one of two categories will be considered separately from the case in which a categorical independent variable falls in one of more than two categories.
Categorical independent variable which falls in one of two categories. Consider a multiple linear regression model with [latex]p = 2[/latex] independent variables, X1, which is age, and X2, which is gender. The dependent variable is the annual salary Y. So the multiple linear regression model is
Regression models assume that the independent variables are quantitative rather than categorical like gender. One solution to this problem is to code the gender as 0 for female and 1 for male. The independent variable X2 in this case is known as a dummy variable or an indicator variable. As a particular instance, consider [latex]n = 6[/latex] data points consisting of three women (ages 26, 71, and 34) and three men (ages 44, 65, and 21). In this case the design matrix is
The elements of the six-element column vector Y are the associated salaries. The value of [latex]\hat \beta_0[/latex] is not meaningful here. Not only is it outside of the scope of the model, its interpretation as the annual salary of a newborn baby girl doesn't fit with societal norms. Newborn baby girls seldom earn annual salaries. The value of [latex]\hat \beta_1[/latex] indicates the increase in annual salary for each additional year in age, adjusted for gender. Since salaries tend to rise over time, we anticipate that [latex]\hat \beta_1[/latex] will be positive. The value of [latex]\hat \beta_2[/latex] indicates the change in salary associated being male rather than female, adjusted for age. If [latex]\hat \beta_2[/latex] is significantly greater than zero, then men's salaries are significantly higher than women's salaries, adjusted for age; if [latex]\hat \beta_2[/latex] is significantly less than zero, then women's salaries are significantly higher than men's salaries, adjusted for age. The choice of using an indicator of 0 for women and 1 for men was arbitrary. See if you can predict what would happen if instead we used 0 for men and 1 for women.
Categorical independent variable which falls in one of more than two categories. Let's extend the regression model to predict the annual salary to include another categorical variable: political affiliation. This categorical variable will have three levels: Republican, Democrat, and Independent. The third category includes anyone who is not affiliated with the two main political parties in the United States. Although it might be tempting to just let [latex]X_3 = 1[/latex] denote a Republican, [latex]X_3 = 2[/latex] denote a Democrat, and [latex]X_3 = 3[/latex] denote an Independent, this will likely produce erroneous results for two reasons. First, using the ordering [latex]X_3 = 1[/latex], [latex]X_3 = 2[/latex], and [latex]X_3 = 3[/latex] implies an ordering of the salaries associated with individuals from the three different political affiliations for [latex]{\beta_3 > 0}[/latex], or the opposite ordering of the salaries associated with individuals from the three political affiliations for [latex]\beta_3 < 0[/latex]. This ordering might not be the correct ordering. Second, leaving a gap of 1 between each of the values of X3 indicates that there is a known and equal salary gap between individuals from the ordered different political affiliations. The usual way to account for a categorical independent variable which can take on c values is to define [latex]c - 1[/latex] independent indicator variables. In the case of political affiliation, the independent variables X3 and X4 can be defined as
and
So now the multiple linear regression model with [latex]p = 4[/latex] independent variables is
In this fashion, the expected value of an Independent's salary is given by
the expected value of an Republican's salary is given by
and the expected value of a Democrat's salary is given by
With this arrangement of the levels of the categorical variable representing the political affiliation, there is no predicted ordering of salaries by the three political affiliations nor are the gaps between the affiliations necessarily equal.
As a particular instance, consider [latex]n = 6[/latex] data points with three women (a 26-year-old Independent, a 71-year-old Democrat, and a 34-year-old Republican) and three men (a 44-year-old Independent, a 65-year-old Democrat, and a 21-year-old Republican) in the study. The appropriate design matrix is
The value of [latex]\hat \beta_3[/latex] is the estimated difference between the mean annual salary of an Independent and a Republican, adjusted for age and gender. The value of [latex]\hat \beta_3[/latex] is the estimated difference between the mean annual salary of an Independent and a Democrat, adjusted for age and gender. This example has been for illustrative purposes only. Estimating five parameters [latex]\beta_0, \, \beta_1, \, \ldots , \beta_4[/latex] from just six data values will almost certainly not provide strong statistical evidence concerning the effect of age, gender, and political affiliation on salary. Furthermore, many other important factors, such as years of education, years on the job, and type of work, have not been included in this regression model.
3.5.2 Interaction Terms
The multiple linear regression model
assumes a linear relationship between each independent variable and Y and the slope associated with an independent variable is identical at all values of the other independent variables within the scope of the multiple linear regression model. This relationship is illustrated for some selected data points of smaller homes from the Ames, Iowa housing data set from Examples 2.9 and 3.10. In this case, X1 is the interior square footage, X2 is an indicator variable reflecting the lot size,
and Y is the sales price. The multiple linear regression model with the [latex]p = 2[/latex] independent variables is
Figure 3.17 shows a scatterplot of the interior square footage and sales price of homes on smaller lots ([latex]X_2 = 0[/latex] as open points) and larger lots ([latex]X_2 = 1[/latex] as solid points). The values of [latex]\hat \beta_0[/latex], [latex]\hat \beta_1[/latex], and [latex]\hat \beta_2[/latex] are indicated on the graph. The estimated intercept [latex]\hat \beta_0 = \text{21,473}[/latex], although slightly outside of the scope of the model, gives the estimated sales price of a small lot containing no dwelling as $21,473. The estimated regression coefficient [latex]\hat \beta_1 = 31.33[/latex] indicates that the sales price of a home increases by an estimated $31.33 for each additional interior square foot, adjusted for lot size. The estimated regression coefficient [latex]\hat \beta_2 = \text{35,693}[/latex] indicates that homes on larger lots cost $35,693 more, on average, than homes on smaller lots, adjusted for interior square feet. Notice that this formulation of the multiple linear regression model forces the slopes of the two lines in Figure 3.17 to be identical, regardless of the value of X2.
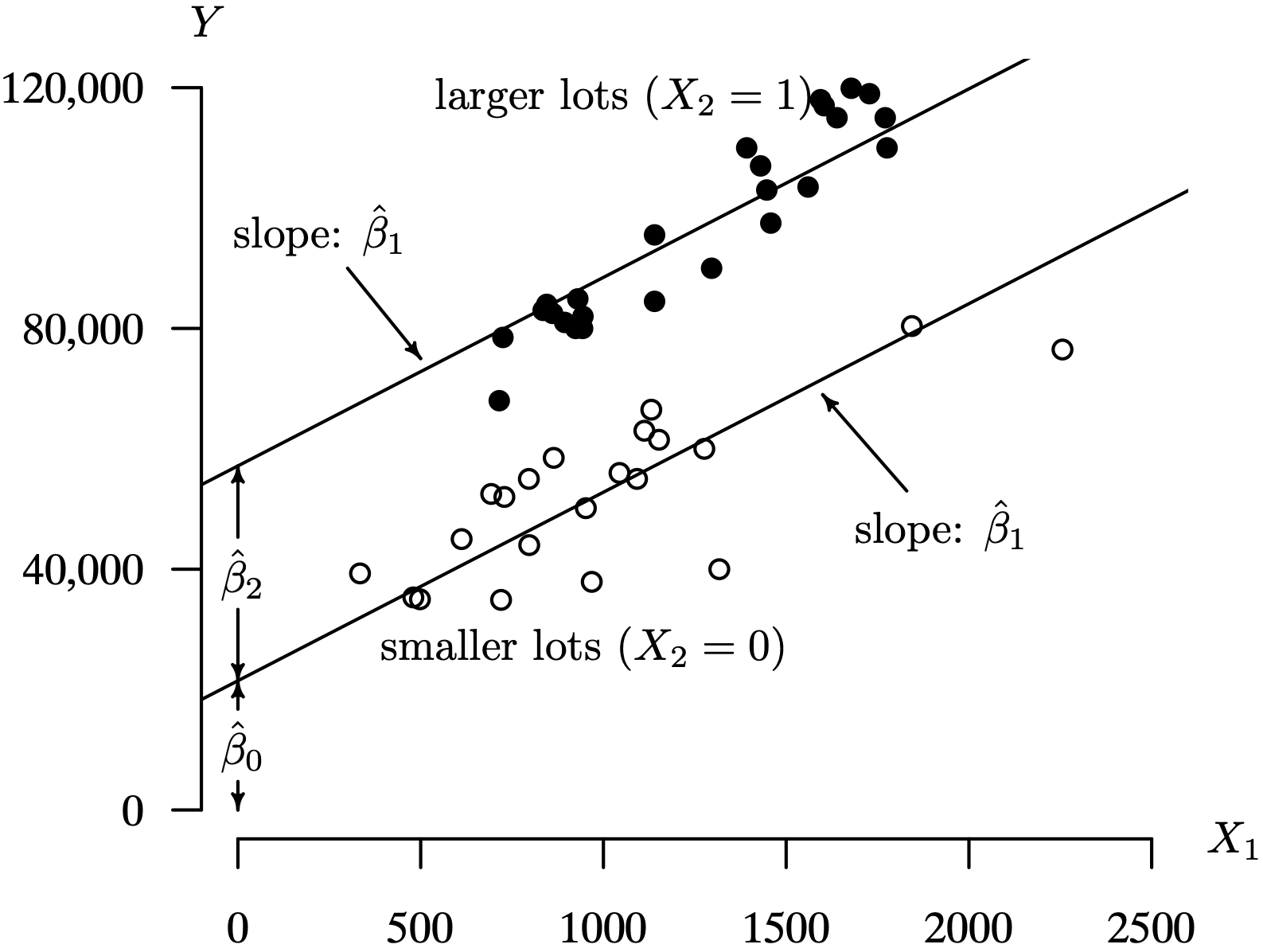
Long Description for Figure 3.17
The horizontal axis labeled X 1 and ranges between 0 to 2500 in increments of 500. The vertical axis labeled Y ranges from 0 to 120,000 in increments of 40,000. The data pairs representing sales price of smaller lots, X equals 0, are indicated in open circle sand those for larger lots, X 2 equals 1 are represented as solid points. Two parallel regression lines, with positive slopes originate from points (0, 20,000) and (0, 50,000). The data pair for smaller lots are clustered around the regression line originating at (0, 20,000) and those for larger lots are clustered around the regression line originating at (0, 50,000). The slope of the regression lines are indicated as beta cap 1. The distance between horizontal axis and regression line originating at (0, 20,000) is indicated as beta cap 0. The distance between the two regression lines is indicated as beta cap 2.
But is the assumption of equal slopes of the two lines in Figure 3.17 justified? Separate simple linear regression models are fitted to the homes built on smaller and larger lots, and the results are plotted in Figure 3.18. The lines do not appear to be parallel in this case, indicating that a more complex regression model is warranted. There appears, in this case, to be an interaction effect between X1 and X2. This means that the effect of one independent variable (X1, for example, the interior size) on Y is altered based on the value of another independent variable (X2, the lot size indicator).
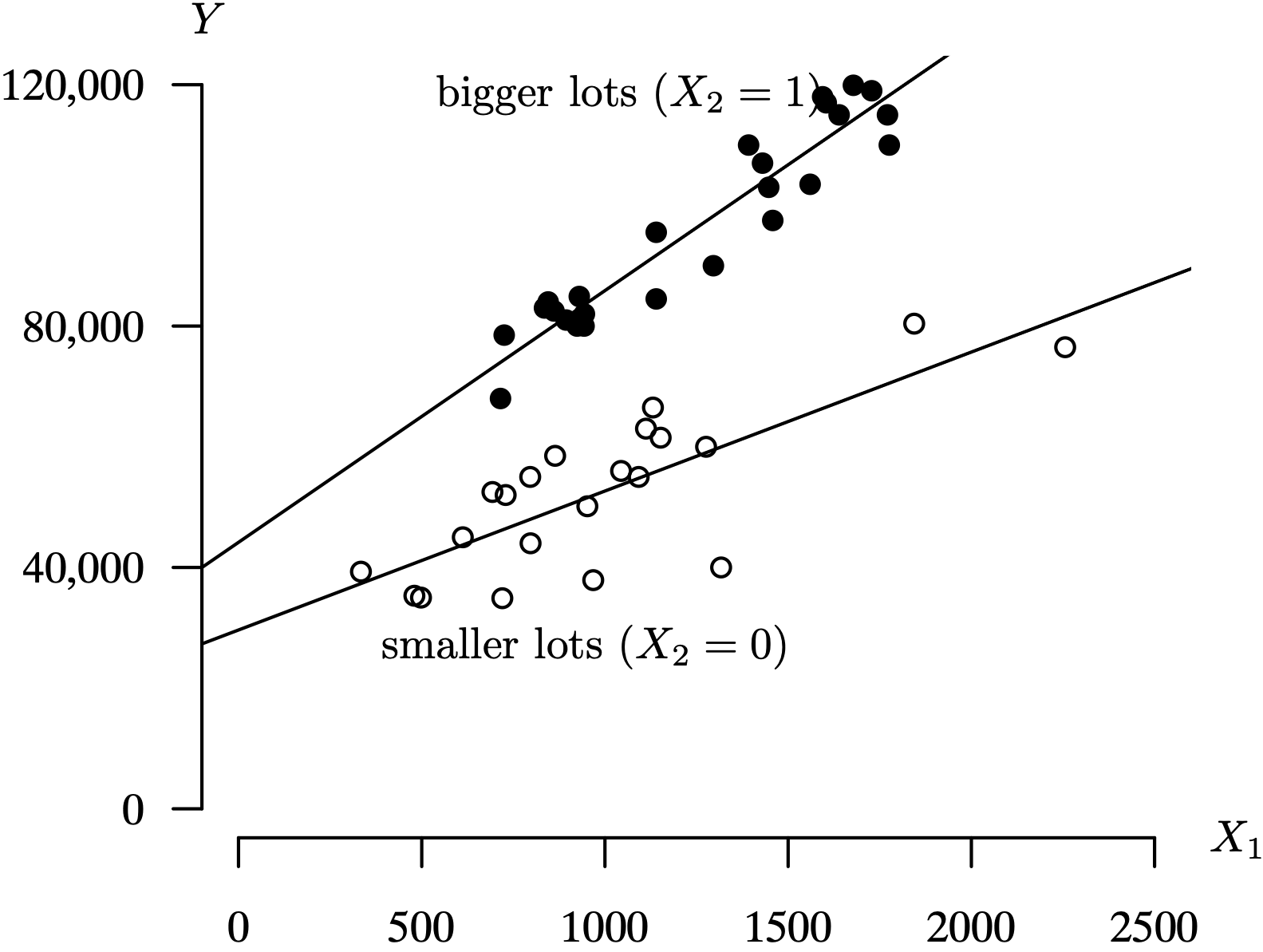
Long Description for Figure 3.18
The horizontal axis labeled X 1 ranges between 0 to 2500 in increments of 500. The vertical axis labeled Y ranges from 0 to 120,000 in increments of 40,000. The data pairs representing the sales price of smaller lots, X equals 0, are indicated in open circle sand those for larger lots, X 2 equals 1 are represented as solid points. Two regression lines, with positive slopes originate from points (0, 30,000) and (0, 40,000). Most of the data pair fall between 500 and 1500 of horizontal axis and 30,000 and 60,000 of vatical axis values. The data pair for smaller lots are clustered around the less steeper regression line originating at (0, 30,000). The data pairs for larger lots are clustered around the regression line, which is a steeper line, originating at (0, 40,000). Most of the data pairs lie between 1000 and 2000 on the horizontal axis and between 70,000 and 120,000 on the vertical axis.
Regression analysts account for this interaction by including cross-product terms in the regression model. In this Ames housing data set example, the regression model with an interaction term is
If the regression parameter [latex]\hat \beta_3[/latex] differs statistically from 0, then the inclusion of the interaction term is warranted. Notice that when [latex]X_2 = 0[/latex] (smaller lots), the model reduces to
which is a simple linear regression model with intercept parameter β0 and slope parameter β1. On the other hand, when [latex]X_2 = 1[/latex] (larger lots), the model reduces to
or
which is a simple linear regression model with intercept parameter [latex]\beta_0 + \beta_2[/latex] and slope parameter [latex]\beta_1 + \beta_3[/latex]. It is in this fashion that the two non-parallel lines depicted in Figure 3.18 can be estimated in a single regression model. Not surprisingly, it requires four parameters, β0, β1, β2, and β3, to do so. The multiple linear regression model with an interaction term can be fitted using the lm function in R by simply replacing the usual + in the formula with *. All four parameters are statistically significant at the 0.05 level in this case, so the inclusion of an interaction term is warranted.
3.5.3 The ANOVA Table
The degrees of freedom for the sums of squares in multiple linear regression are modified because of the additional parameters estimated relative to those given in the ANOVA table from Table 2.2 for simple linear regression. The ANOVA table for a multiple linear regression model with p independent variables and normal error terms is given in Table 3.6.
|
Source |
SS |
df |
MS |
F |
|---|---|---|---|---|
|
Regression |
SSR |
p |
MSR |
[latex]MSR / MSE[/latex] |
|
Error |
SSE |
[latex]n - p - 1[/latex] |
MSE |
|
|
Total |
SST |
[latex]n - 1[/latex] |
Formulas for the sums of squares using the matrix formulation for multiple linear regression are [latex]SST = SSR + SSE[/latex], which is
where [latex]\bar {\bf Y}[/latex] is an n-element column vector with identical elements which are each the sample mean of the values of the dependent variable. Equivalently,
where [latex]\bf{J}[/latex] is an [latex]n \times n[/latex] matrix with all elements being equal to 1. The mean square error for regression is [latex]MSR = SSR / p[/latex], the mean square error is [latex]MSE = SSE / (n - p - 1)[/latex], and the test statistic [latex]F = MSR / MSE[/latex] can be used for testing
versus
where F has an [latex]F(p, \, n - p - 1)[/latex] distribution under H0. The anova function in R can be used to generate an ANOVA table associated with a multiple linear regression model fitted by the lm function. For the Ames, Iowa housing data from Example 3.10 which used [latex]p = 2[/latex] independent variables (interior square footage and lot size), the R summary function returns the test statistic [latex]F = 5.322[/latex], which is associated with a p-value of [latex]p = 0.006[/latex] based on the F distribution with [latex]p = 2[/latex] and [latex]n - p - 1 = 120 - 2 - 1 =117[/latex] degrees of freedom. There is strong statistical evidence that one or both of the coefficients [latex]\hat \beta_1[/latex] and [latex]\hat \beta_2[/latex] is statistically different from zero. One or both of the independent variables is effective in predicting the sales price.
3.5.4 Adjusted Coefficient of Determination
The coefficient of determination for a multiple linear regression model is defined as
and it measures the fraction of variation in [latex]Y_1, \, Y_2, \, \ldots, \, Y_n[/latex] about [latex]\bar Y[/latex] that is accounted for by the linear relationship between the independent variables [latex]X_1, \, X_2, \, \ldots, \, X_p[/latex] and Y. As before [latex]0 \le R ^ 2 \le 1[/latex], and the extreme cases are associated with [latex]\hat \beta_1 = \hat \beta_2 = \cdots = \hat \beta_p = 0[/latex] (for [latex]R ^ 2 = 0[/latex]) and all Y-values falling in the estimated regression hyperplane (for [latex]R ^ 2 = 1[/latex]).
Now consider a multiple linear regression model with p independent variables [latex]X_1, \, X_2, \, \ldots, \, X_p[/latex]. What is the effect on SST and SSE of adding another independent variable, [latex]X_{p + 1}[/latex], to the model? Adding another independent variable does not affect SST because it depends only on [latex]Y_1, \, Y_2, \, \ldots, \, Y_n[/latex]. The value of SSE cannot increase with the addition of the new independent variable because either (a) SSE will remain the same if [latex]\hat \beta_{p + 1} = 0[/latex], or (b) SSE will decrease if [latex]\hat \beta_{p + 1} \ne 0[/latex]. The impact on R2 is that it must stay the same or increase for every additional independent variable that is added to the model.
It is for this reason that R2 tends to be a biased estimator of the fraction of variation in [latex]Y_1, \, Y_2, \, \ldots, \, Y_n[/latex] accounted for by the independent variables. Some regression software (including R) calculate an adjusted coefficient of variation by dividing the sums of squares by their associated degrees of freedom
Both values are reported in the call to the summary function with the Ames, Iowa housing data in Example 3.10 as
3.5.5 Multicollinearity
In many settings, the values of the independent variables are correlated. In the housing data set from Example 3.10, for example, the independent variables X1 (interior square footage) and X2 (lot size) are probably positively correlated. Intuition suggests that larger homes are built on larger lots, on average. In the extreme case, what if homes in Ames were required by some bizarre municipal code to all be single story homes with the square footage of the lot always exactly four times the square footage of the interior of the home? In this case, [latex]X_2 = 4 X_1[/latex], so knowing the value of either X1 or X2 allows you to know the value of the other. Intuitively, one of the two independent variables is superfluous. When this is the case, the design matrix [latex]{\bf X}[/latex] has two columns which are multiples of one another, so these columns are linearly dependent and the matrix does not have full rank. This implies that the matrix [latex]{\bf X} ^ \prime {\bf X}[/latex] (which is used in computing the estimates of the regression coefficients) is singular, so it does not have an inverse. In this case, the usual formula for the regression coefficients,
is undefined because the matrix [latex]{\bf X} ^ \prime {\bf X}[/latex] does not have an inverse. In the case in which [latex]X_2 = 4 X_1[/latex], all pairs of the independent variables fall on a line, so it is impossible to know the proper tilt of the fitted regression plane in [latex]{\cal R} ^ 3[/latex]. There are many planes that minimize the sum of squared errors.
Multicollinearity is the condition associated with independent variables that are highly correlated among themselves in a multiple regression model. More specifically, multicollinearity occurs when two or more of the independent variables have a high correlation. This can appear as an approximately linear relationship between two of the independent variables. Multicollinearity is a condition associated with the design matrix [latex]{\bf X}[/latex] rather than the values of the dependent variable [latex]{\bf Y}[/latex] or the model [latex]{\bf Y} = {\bf X} {\pmb{\beta}} + {\pmb{\epsilon}}[/latex]. In cases in which multicollinearity exists, the matrix [latex]{\bf X} ^ \prime {\bf X}[/latex] has an inverse, but it is ill-conditioned and subject to slight variations in the data or is unstable because of large differences in the magnitudes of the various values of the independent variables. One of the key practical issues when multicollinearity is present is that an estimated regression coefficient for a particular independent variable depends on whether the other independent variables are included or left out of the model.
So multicollinearity has been loosely defined as high correlation among the independent variables. There is redundancy to the information contained in the independent variables. The next paragraphs describe how to detect multicollinearity, its consequences, and some remedies.
Although the hypothetical perfect correlation between the interior space and the lot size of a home from Ames, Iowa described previously occurs seldom in practice, highly correlated independent variables can result in some unusual behavior of regression coefficients as a regression model is constructed. Some signs that multicollinearity might be present in a multiple linear regression model include the following.
- Large values of the estimated standard deviations of the regression coefficients.
- Including or not including an independent variable in the model results in large changes to the estimated regression coefficients.
- An estimated regression coefficient that is statistically significant when the associated independent variable is considered alone, but becomes insignificant when one or more other independent variables are added to the model.
- An estimated regression coefficient with a sign that is inconsistent with expected sign or inconsistent with previous similar data sets.
- The pairwise sample correlation among the independent variables is high. The cor function in R can be used to assess the correlation among independent variables. The R statement

for example, calculates the correlation matrix for the columns of the built-in data frame named swiss. The off-diagonal elements of this matrix range from [latex]-0.69[/latex] to 0.70, indicating that multicollinearity is present.
All of the criteria listed above are informal. A more formal way to determine whether multicollinearity is present is to introduce a statistic which reflects multicollinearity. The estimate of the variance of [latex]\hat \beta _ j[/latex] can be written as
where [latex]\bar X_j = \sum_{i\,=\,1}^n X_{ij}[/latex], [latex]MSE = SSE / (n - p - 1)[/latex] for the full multiple regression model, and [latex]R_j^2[/latex] is the coefficient of determination obtained by conducting a multiple linear regression with Xj as the dependent variable and the other [latex]p - 1[/latex] X-values as the independent variables, for [latex]j = 1, \, 2, \, \ldots, \, p[/latex]. The coefficient on the right-hand side of this equation,
is known as a variance inflation factor for independent variable j, for [latex]j = 1, \, 2, \, \ldots, \, p[/latex]. In the extreme case when [latex]R_j^2 = 0[/latex], the associated variance inflation factor is [latex]VIF_j = 1[/latex]. This corresponds to the case in which Xj is not linearly related to the other independent variables. As [latex]R_j^2[/latex] increases, [latex]VIF_j[/latex] also increases, corresponding to increased correlation between the independent variables. When the largest of the [latex]VIF_j[/latex] values exceeds the threshold value of 10, one can conclude that the multicollinearity is present among the independent variables.
The R code below calculates the variance inflation factors for the data values in the swiss data frame, where the independent variables
- X1, the percentage of males involved in agriculture as an occupation,
- X2, the percentage of draftees receiving the highest make on an army examination,
- X3, the percentage of draftees with education beyond the primary school,
- X4, the percentage of Catholics, and
- X5, the percentage of live births who live less than one year,
are used to predict Y, a common standardized fertility measure, from the [latex]n = 47[/latex] French-speaking provinces of Switzerland in about the year 1888. The R code below computes the variance inflation factors for the [latex]p = 5[/latex] independent variables.

The variance inflation factors for the [latex]p = 5[/latex] independent variables are
Since none of these five values exceeds 10, we can conclude that the multicollinearity that exists in the independent variables is not strong enough to cause concern. (Some regression analysts use 5 as a threshold rather than 10.) Some keystrokes can be saved by using the vif function from the car package on a multiple linear regression model fitted by the lm function.

One popular remedy for multicollinearity is known as ridge regression, which is a parameter estimation technique that abandons the requirement of unbiased parameter estimates. The approach taken with ridge regression is to choose estimates for the regression parameters that are biased, but have a smaller variance than the ordinary least squares estimates. The goal is to generate parameter estimates with tolerable bias but smaller variance. The typical approach used in statistics to overcome this bias/variability trade-off is to use the estimates that minimize the mean square errors. Assuming that the X and Y values have been centered, we can dispense with the need for an intercept term in the multiple regression model. Rather than minimizing the usual sum of squared errors
ridge regression minimizes
There are now two terms in the modified sum of squares. The second term in SR is known as the penalty term. The new parameter λ is known as the penalty parameter. When [latex]\lambda = 0[/latex], [latex]S_R[/latex], reduces to the ordinary least squares case and achieves a value SSE at the ordinary least squares estimators. As λ increases, the estimators converge to [latex]\hat \beta_1 = \hat \beta_2 = \cdots = \beta_p = 0[/latex]. We desire a λ value that introduces some bias into the parameter estimates, but also have a reduced variance.
The geometry associated with ridge regression for [latex]p = 2[/latex] independent variables X1 and X2 in a multiple linear regression model is illustrated in Figure 3.19. The ellipses are level surfaces of the first term in [latex]S_R[/latex]. The center of the ellipses is the ordinary least squares estimators of [latex](\beta_1, \, \beta_2) = \big( \hat \beta_1, \, \hat \beta_2 \big)[/latex], which are the values that minimize the first term of [latex]S_R[/latex]. The circles centered at the origin are level surfaces of the second term in [latex]S_R[/latex]. The ridge regression estimators for β1 and β2 will occur at the intersection of one of elliptical and circular contours. In Figure 3.19 the two outermost level surfaces intersect at a point, which is a value of the ridge regression estimates of β1 and β2 which correspond to one particular value of the penalty parameter λ. The point at which this intersection occurs is a function of the penalty parameter λ. In higher dimensions, the circles become spheres and the ellipses become ellipsoids.
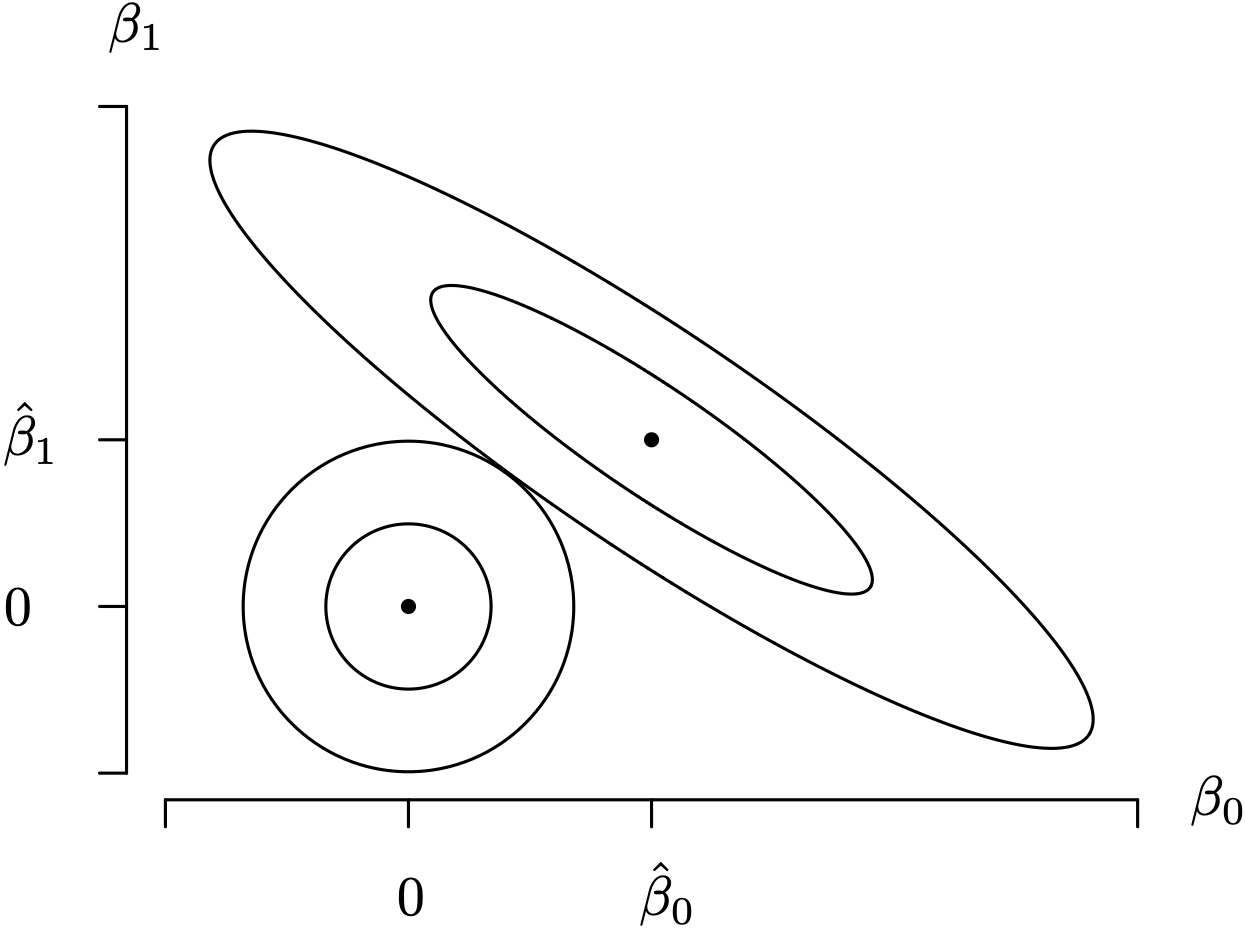
Long Description for Figure 3.19
The horizontal axis labeled beta 0 contains the points 0 and beta cap 0. The vertical axis labeled beta 1 contains the points 0 and beta cap 1. A point plotted at beta cap 0, beta cap 1 is surrounded by two concentric elliptical contours. Another point plotted at 0, 0 is surrounded by two concentric circles. The outermost levels of the elliptical and circle contours intersect at a point between 0 and beta cap 0 of the horizontal axis and 0 and beta cap 1 of the vertical axis.
Determining the value of the penalty parameter is critical in ridge regression, but its choice depends on the regression model and associated data set. A common technique for determining an optimal value for λ is known as k-fold cross-validation. There are several functions in R which can perform ridge regression: the lm.ridge function from the MASS package, the linearRidge function from the ridge package, and the glmnet function from the glmnet package. Ridge regression is related to the lasso (least absolute shrinkage and selection operator) estimator and elastic net regularization, two other popular parameter estimation techniques that are often applied for large values of p.
Is there a way to completely avoid multicollinearity? In some settings, the answer is yes. When the values of the independent variables are chosen so that they are uncorrelated, the regression coefficients associated with a simple linear regression model of each independent variable separately match the regression coefficients of any model involving more independent variables. This fact provides a strong argument for a designed experiment which can result in uncorrelated independent variables whenever the setting of the regression problem make this possible.
3.5.6 Model Selection
It is common in regression modeling to have a large number of potential independent variables that might adequately predict the dependent variable Y that need to be sifted through in order to decide whether each should be included or excluded from the regression model. If there are p potential independent variables in the multiple linear regression model
then there are 2p possible regression models (always including an intercept term and not considering interaction terms or nonlinear terms) because each independent variable will either be included or not included in the regression model. Since the number of regression models to fit can be daunting, even for moderate values of p, we desire an algorithm for selecting the appropriate independent variables to include in the model. Forward stepwise regression is one such automatic search procedure used to select the independent variables to include in a multiple linear regression model. The procedure begins with the null model [latex]Y = \beta_0 + \epsilon[/latex] and progressively adds independent variables to the model that are deemed to be statistically significant. In the initial step, p simple linear regression models are fit for each potential independent variable. The independent variable with the smallest p-value falling below a prescribed threshold (commonly, [latex]\alpha = 0.05[/latex]) associated with the t-test described in Section 2.3.2 is added to the model. In the second step, [latex]p - 1[/latex] multiple linear regression models with two independent variables are fitted using the previously selected independent variable and each of the other potential independent variables. The independent variable with the smallest p-value is added to the model. This process continues until no more independent variables meet the criteria. This is the multiple linear regression model selected by forward stepwise regression. Several other variants of forward stepwise regression and other model selection algorithms are outlined below.
- Foreward stepwise regression often includes a test to determine whether independent variables that have previously been added to the model have p-values that exceed the threshold and should consequently be removed from the model.
- Backward stepwise regression starts by including all p independent variables in the regression model and eliminates the independent variable with the largest p-value on each step. Unfortunately, there is no guarantee that forward stepwise regression and backward stepwise regression will result in the same final regression model.
- Once this statistically significant independent variables have been identified, a similar stepwise procedure can be executed to test for statistically significant interaction terms.
- A similar stepwise procedure can be executed to test for the significance of nonlinear terms in the regression model.
- With increased computer speeds and a moderate value of p, the number of independent variables, it is possible to fit all 2p possible regression models and compare them to determine an appropriate final regression model.
- Comparing potential regression models using p-values is not universal. The Akaike Information Criterion (AIC) is a measure which extracts a penalty for each additional parameter in a model in an effort to avoid overfitting.In summary, selecting a multiple linear regression model is not easy. The skills required to select a model include the ability to (a) detect and remedy multicollinearity, (b) assess evidence of interaction effects between independent variables and include them in the model when appropriate, (c) assess evidence of nonlinear relationships between some or all of the independent variables and the dependent variable and include appropriate terms in the model, (d) execute the appropriate multidimensional diagnostic procedures (outlined in the simple linear regression case in Section 3.2) and execute the appropriate remedial procedures (outlined in the simple linear regression case in Section 3.3) when model assumptions are violated, and (e) assess the normality of the residuals.
3.6 Weighted Least Squares
The three approaches to estimating the parameters in a simple linear regression model that we have encountered thus far,
- the algebraic approach,
- the matrix approach,
- using the R lm (linear model) function,
all have the same assumptions regarding the independent variable, the dependent variable, and the model [latex]Y = \beta_0 + \beta_1 X + \epsilon[/latex]. In all three approaches, the error terms are assumed to be mutually independent random variables, each with population mean 0 and population variance–covariance matrix [latex]V[\epsilon] = \sigma _ Z ^ {\, 2} I[/latex], where I is the [latex]n \times n[/latex] identity matrix. This means that [latex]V[ \epsilon_i ] = \sigma _ Z ^ {\, 2}[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. There is also an implicit assumption that each of the data pairs [latex](X_i, \, Y_i)[/latex] are each given equal weight in the regression.
Settings occasionally arise in which some data values should be given different weights. There might be evidence that some of the Yi values have more precision than others. Weights can be placed on each of the data pairs to account for this difference in precision. This leads to a weighted least squares approach to estimating the coefficients in a regression model.
In the standard simple linear regression model, the assumption
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], means that the variance of the dependent variable from the regression line is equal for all of the n data pairs, regardless of the value of the independent variable. In weighted least squares modeling, the positive weights [latex]w_1, \, w_2, \, \ldots , \, w_n[/latex] are determined so that
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], which means that certain data pairs have more precision than other data pairs. The weights are fixed constants. There is no requirement that the weights sum to one. Data pairs with larger weights are assumed to have a lower variability to their error terms. This allows for a population variance that changes from one data pair to another.
As an illustration, the values of the dependent variable Y might be sample means at the various values of the independent variable X. Furthermore, if the sample sizes associated with the sample means are known and unequal, then we would like to assign higher weights to the data pairs associated with larger sample sizes. If ni is the sample size for data pair i, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], then the appropriate weight for data pair i is [latex]w_i = n_i[/latex] so that
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
So rather than minimizing the sum of squares
as was the case in the standard simple linear regression model, weighted least squares minimizes the weighted sum of squares
Notice that this reduces to the ordinary sum of squares when [latex]w_1 = w_2 = \cdots = w_n = 1[/latex]. As before, calculus can be used to minimize S with respect to β0 and β1 to arrive at the least squares estimators [latex]\beta_0[/latex] and [latex]\beta_1[/latex]. The partial derivatives of S with respect to β0 and β1 are
and
These can be simplified to give the normal equations
and
The normal equations are a system of two linear equations in the two unknowns β0 and β1, given the data pairs [latex](X_1, \, Y_1), \, (X_2, \, Y_2), \, \ldots , \, (X_n, \, Y_n)[/latex] and the weights [latex]w_1, \, w_2, \, \ldots, \, w_n[/latex]. The normal equations can be solved to yield the weighted least squares estimators. This derivation constitutes a proof of the following theorem.
The matrix approach can also be applied to weighted least squares. Define the [latex]{\bf X}[/latex], [latex]{\bf Y}[/latex], [latex]\pmb{\beta}[/latex] and [latex]\pmb{\epsilon}[/latex] matrices as in Section 3.4:
In addition, assume that the matrix [latex]{\bf W}[/latex] is a diagonal matrix with the weights [latex]w_1, \, w_2, \, \ldots, \, w_n[/latex] on the diagonal:
In this case, the normal equations can be written in matrix form as
Pre-multiplying both sides of this equation by [latex]\left( {\bf X} ^ \prime {\bf W} {\bf X} \right) ^ {-1}[/latex] gives the least squares estimators for the regression parameters in matrix form as
As before, the fitted values can also be written in matrix form as
or
The residuals [latex]e_i = Y_i - \hat{Y}_i[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], can also be written in matrix form as
where [latex]{\bf e}[/latex] is the column vector of residuals [latex]{\bf e} = (e_1, \, e_2, \, \ldots , \, e_n) ^ \prime[/latex]. These matrix results are summarized in the following theorem.
The algebraic approach, matrix approach, and R approach to weighted least squares problem will be illustrated in the next example. Establishing the weights [latex]w_1, \, w_2, \, \ldots, \, w_n[/latex] can be a nontrivial problem, and differs depending on the setting in which the weighted regression model is employed.
Using simple linear regression in the previous example, either weighted or unweighted, might not be the best approach. The dependent variable Y is the probability that an item of age X is functioning. This dependent variable must lie between 0 and 1, but the regression line could potentially fall outside of that range within the scope of the model. Two potential remedies are given in the next two sections: using a regression model with nonlinear terms such as X2 or X3, or a survivor function of a lifetime model rather than a line, or a nonlinear model known as a logistic regression model, whose dependent variable necessarily lies between 0 and 1.
3.7 Regression Models with Nonlinear Terms
Regression models with nonlinear terms arise frequently in regression modeling. One simple example is polynomial regression. A quadratic regression model, for example, is
where β0, β1, and β2 are the regression coefficients, and ϵ is a white noise term. This model is still linear in β0, β1, and β2. One way to think about this model is to consider X and X2 to be the [latex]p = 2[/latex] independent variables in a multiple regression model. The next example fits a quadratic model to the data pairs in which the independent variable X is the speed of an automobile and the dependent variable Y is its stopping distance.
Nonlinear regression modeling is not limited to just polynomial regression models. The next two examples fit the same data set concerning the national debt in the United States between 1970 and 2020 to a nonlinear regression model using two fundamentally different approaches. The first approach is to transform the nonlinear regression model to a linear regression model and then apply the standard techniques for parameter estimation to the transformed model. The second approach is to use numerical methods to minimize the sum of squares in the usual least squares fashion described previously.
There is a second approach to fitting an exponential regression model to the national debt data pairs that follows the standard approach to least squares estimation, which is given next.
One drawback that emerged from the survival function estimation example from the previous section (involving current status data) is that fitting a regression line results in a survival probability that can be negative or greater than one when extrapolated outside of the range of the independent variable in the data pairs. In addition, the estimated probability of survival at time zero for both the ordinary simple linear regression model and the weighted simple linear regression model seemed low. Typically, a brand-new item is not defective. A nonlinear regression function is an attractive alternative model in this particular setting. The next example combines a nonlinear regression model and weighted least squares estimators to provide an improved regression model.
3.8 Logistic Regression
Logistic regression is appropriate when the dependent variable Y can assume one of two values: zero and one. This is sometimes known as a binary or dichotomous response variable. For now, to keep the mathematics and interpretations simple, assume that there is a single predictor X. This is known as a simple logistic regression model, and is a special type of nonlinear regression model. Including multiple independent variables in a logistic regression model is a straightforward extension. For dichotomous data, instead of predicting 0 or 1, we predict the probability of getting a 1 [that is, [latex]P(Y = 1)[/latex]]. So we need a regression model that predicts values of the interval [latex][0, \, 1][/latex].
The following example will be used throughout this section to motivate the need for a special model to accommodate a binary dependent variable, and to illustrate the techniques for the estimation of the model parameters.
One of the initial considerations in developing a statistical model for the outcome of a field goal as a function of the length of the field goal attempt is to find a function that will only assume values between 0 and 1. A diagram that gives some guidance with regard to this function is to batch the data into 5-year increments. So the bins are all field goals that fall in the ranges [latex]20 \pm 2, \, 25 \pm 2, \, \ldots , \, 60 \pm 2[/latex]. This window is long enough so that the random sampling variability associated with nearby attempts is damped considerably, and yet short enough so that outcome patterns as a function of yardage are still apparent. The R code below batches the independent variable into the 5-yard increments and plots the estimated probability of success for attempts in each batch at its midpoint. This estimated probability is just the fraction of successful field goals within a particular range. Furthermore, the area of each point plotted is proportional to the number of attempts in that particular bin. For example, there were 79 attempts in the first bin (18–22 yards) and only 4 attempts in the last bin (58–62 yards). The R code below reads a data set off of the web that contains the results of [latex]n = 948[/latex] NFL field goal attempts during 2003. The data consists of columns that give the length of the field goal attempt and the outcome, failure ([latex]Y = 0[/latex]) or success ([latex]Y = 1[/latex]). The R code rounds each length to the nearest 5 yards, and plots the midpoint of the rounded field goal lengths versus the estimated probability of success.

While the performance of NFL field goal kickers varies from one kicker to the next, these points give us an idea of what we would like for a smooth regression function in this setting.
The results are shown in Figure 3.28. It is clear that the estimated probability of making a field goal decreases as the length of the field goal attempt increases, as one would expect. There is a strong relationship between the length of the field goal attempt and the probability of success. Our goal is to fit a nonlinear regression function to the raw data values that smooths the random sampling variability and can be used for the purpose of prediction.
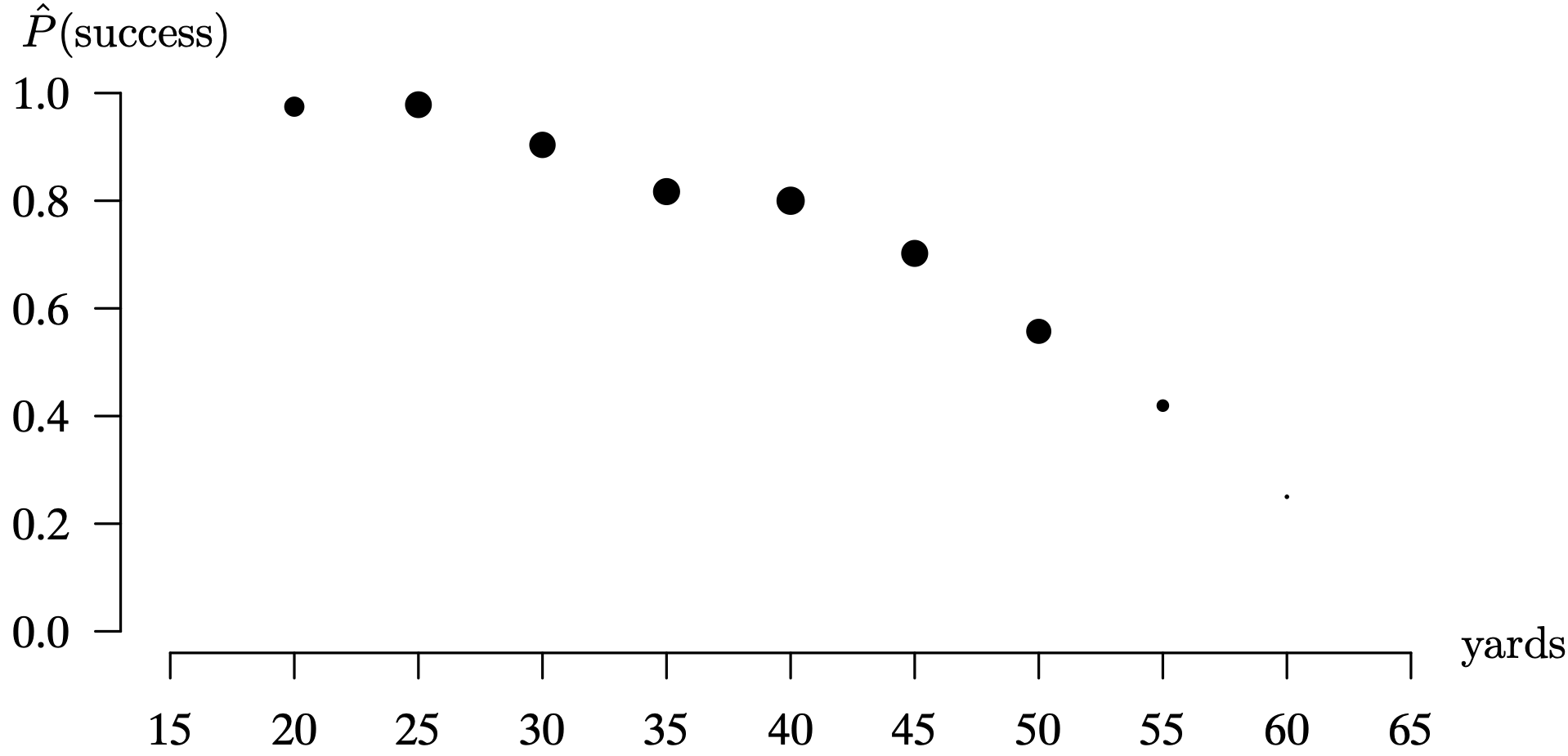
Long Description for Figure 3.28
The horizontal axis ranges from 15 to 65 in increments of 5. The vertical axis ranges from 0 to 1.0 in increments of 0.2. The data points are plotted at (20,1); (25, 1); (30, 0.9); (35, 0.8); (40, 0.8); (45, 0.7); (50, 0.6), (55, 0.5). As the length of field increases, the success of goal decreases.
When the dependent variable only takes on the values zero and one, the usual mean response function for the simple linear regression model
is
where [latex]E[Y][/latex] denotes the conditional expected value of Y given a particular setting of the independent variable X. This mean response function does not limit the values of Y to just zero and one. With normally distributed error terms, this model would allow for Y values which could be less than 0 or greater than 1.
In logistic regression, this type of curve, regardless of whether it begins near one and ends near zero or it begins near zero and ends near one, is known as a sigmoidal response function. A natural choice for the sigmoidal response function is a cumulative distribution function associated with a random variable, or its complement (the survivor function). Three popular probability distributions whose cumulative distribution functions are used in logistic regression are the standard logistic distribution (also commonly called the logit model), the standard normal distribution (also commonly called the probit model), and the standard extreme value distribution (also commonly called the complimentary log-log model). These are described in the next paragraph.
The standard logistic distribution has probability density function
and cumulative distribution function
The probability density function is symmetric about the population mean [latex]E[X] = 0[/latex] and has population variance [latex]V[X] = \pi ^ 2 / 3[/latex]. The standard normal distribution has probability density function
and cumulative distribution function
The probability density function is also symmetric about the population mean [latex]E[X] = 0[/latex] and has population variance [latex]V[X] = 1[/latex]. The probability density function for the standard logistic distribution is similar in shape (that is, bell-shape) to that for the standard normal distribution, but has heavier tails. The symmetry of the probability density functions for the standard logistic distribution and the standard normal distribution limits the shape of the associated cumulative distribution function. A nonsymmetric distribution often provides a better fit. This leads to a search for a probability distribution with a nonsymmetric probability density function. One such probability distribution is the extreme value distribution. The standard extreme value distribution has probability density function
and cumulative distribution function
The population mean and the population variance are not mathematically tractable, but the numeric values, to ten digits, are
The probability density function is not symmetric about the mean.
The R code below plots these three probability density functions on the same set of axes. The standard normal probability density function is taken directly from the formulas in the previous paragraph. The probability density functions for the standard logistic distribution and the standard extreme value distribution have been standardized (by subtracting their population mean and dividing by the population standard deviation) so that all three probability density functions can be viewed on an equal footing. The plot emphasizes the shape of the various probability density functions.

The results are displayed in Figure 3.29. All three probability distributions have support on the entire real number line [latex]-\infty < x < \infty[/latex], although the graph only includes the values within three standard deviation units from the population mean. As expected, the probability density functions for the standard normal distribution and the standardized version of the standard logistic distribution are symmetric and bell-shaped. The probability density function of the standardized version of the standard extreme value distribution is nonsymmetric. The R code below plots the cumulative distribution function associated with the standardized version of the standard logistic distribution.
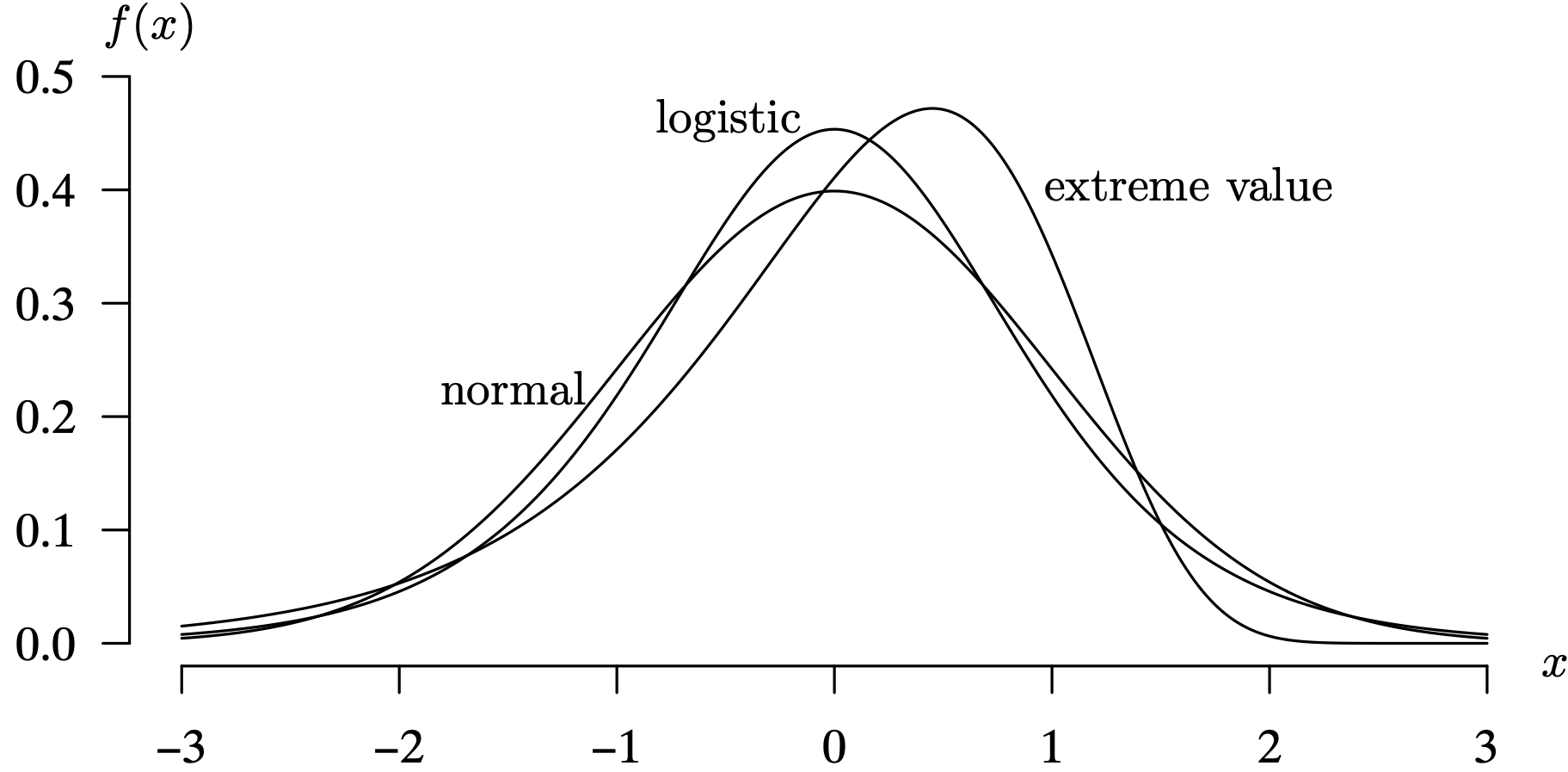
Long Description for Figure 3.29
The horizontal axis ranges from negative 3 to 3 in increments of 1. The vertical axis ranges from 0 to 0.5 in increments of 0.1. The normal distribution and logistics distributions are represented by bell shaped curves with mean 0 and same standard deviation. The curves originate at negative (3, 0), and fall back to( 3, 0). Normal distribution peaks at (0, 0.38) but logistic distribution peaks at (0, 0.45). The extreme value probability distribution is left skewed, with the mean at 0.5. It originates at negative (3, 0), peaks at (1, .46) and falls back to (3, 0).
The cumulative distribution function [latex]F(x) = P(X \le x)[/latex] is graphed in Figure 3.30. This cumulative distribution function is monotone increasing and satisfies [latex]\lim_{x \, \rightarrow \, - \infty} F(x) = 0[/latex] and [latex]\lim_{x \, \rightarrow \, \infty} F(x) = 1[/latex]. Notice that a plot of [latex]F(-x)[/latex] gives the complement of the cumulative distribution function. In other words, [latex]S(x) = 1 - F(x) = P(X \ge x)[/latex]. This function is monotone decreasing and satisfies [latex]\lim_{x \, \rightarrow \, - \infty} S(x) = 1[/latex] and [latex]\lim_{x \, \rightarrow \, \infty} S(x) = 0[/latex]. This function is known in survival analysis as the survivor function.
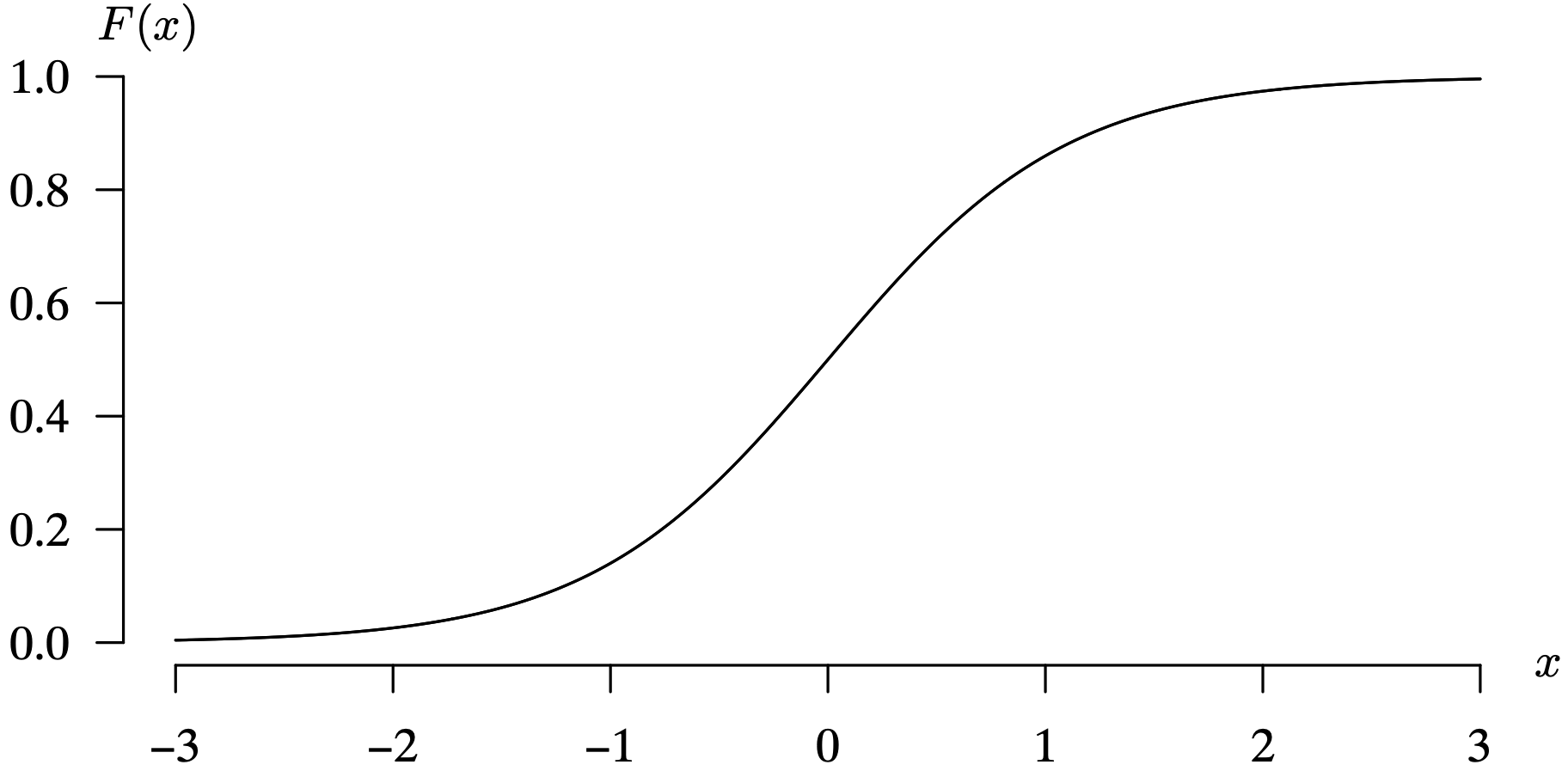
Now that cumulative distribution functions and their complements have been identified as a reasonable way to estimate the probability of success for the field goal data, we would like to establish a mechanism for incorporating the value of the predictor X into the probability model. The emphasis here will be on using the cumulative distribution function for the logistic distribution, since that seems to be the most commonly used in logistic regression.
The usual form of the mean response function for simple linear regression is
But in the case of a binary outcome, the constraint
must be imposed. This is done naturally using the cumulative distribution functions and their complements for the various probability distributions described earlier. Let [latex]\pi (X)[/latex] be the mean response function for a regression model with a binary response. Using the cumulative distribution function for the logistic distribution, the mean response function is
Since the random variable Y can only assume the values 0 and 1 for a particular value of X, it is a Bernoulli random variable with probability of success [latex]\pi(X)[/latex]. Since the expected value and the probability that a Bernoulli random variable assumes the value 1 are equal, the mean response function can also be expressed as
where [latex]P(Y = 1)[/latex] is the probability that the dependent variable Y equals 1 for a particular fixed setting of the independent variable X. The parameters β0 and β1 assume the following roles.
- The sign of β1 controls whether the mean response function is monotone increasing or decreasing. Table 3.9 shows the direction of the relationship associated with the sign of β1. The statistical significance of the point estimator of β1 depends on its magnitude.
- The magnitude of β1 controls the steepness of the mean response function, with larger magnitudes corresponding to steeper mean response functions.
- The value of β0 controls the location of the mean response function on the X-axis.
|
Condition |
[latex]\displaystyle{\lim_{X \, \rightarrow \, - \infty} \pi(X)}[/latex] |
[latex]\displaystyle{\lim_{X \, \rightarrow \, \infty} \pi(X)}[/latex] |
|---|---|---|
|
[latex]\beta_1 < 0[/latex] |
1 |
0 |
|
[latex]\beta_1 > 0[/latex] |
0 |
1 |
|
[latex]\beta_1 = 0[/latex] |
[latex]e ^ {\beta_0} / \left( 1 + e ^ {\beta_0} \right)[/latex] |
[latex]e ^ {\beta_0} / \left( 1 + e ^ {\beta_0} \right)[/latex] |
A graph that illustrates the effect of varying values of β1 for the fixed value of [latex]\beta_0 = 0[/latex] on the mean response function [latex]\pi(X)[/latex] is given in Figure 3.31. As expected, the mean response function [latex]\pi(X)[/latex] is monotone decreasing for [latex]\beta_1 < 1[/latex] and monotone increasing for [latex]\beta_1 > 1[/latex]. The mean response function is steeper as the magnitude of β1 increases.
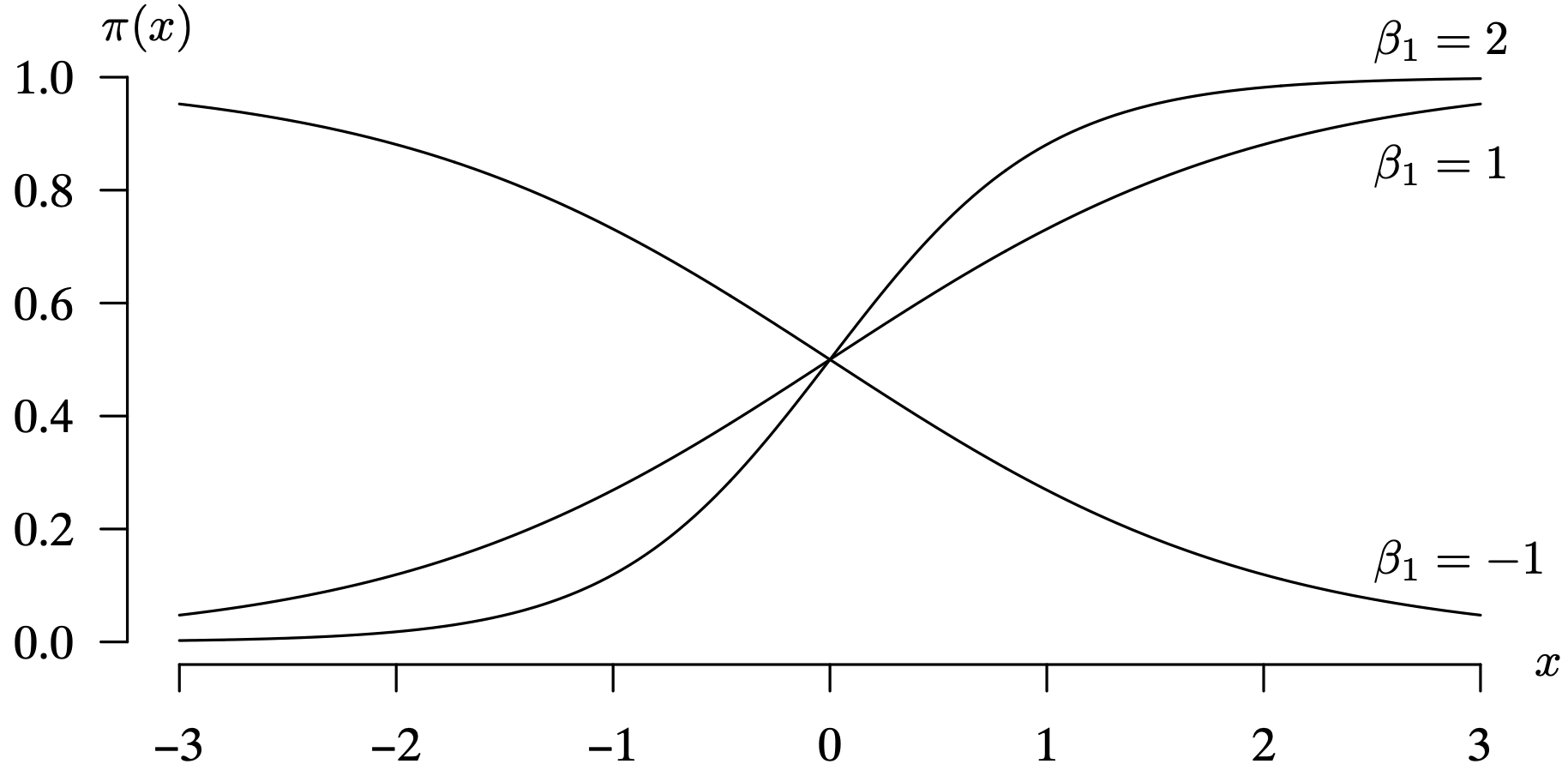
Long Description for Figure 3.31
The horizontal axis ranges from negative 3 to 3 in increments of 1. The vertical axis ranges from 0 to 1.0 in increments of 0.2. Beta subscript 2 is a S-shaped curve that passes through the points (negative 3, 0); (negative 1, 0.1); (0, .5); (1, 0.8); (2, 1); (3,1). Beta subscript 1 equals 1 passes through points (negative 3, 0.02); (negative 1, 0.2); (0, 0.4); (1, 0.7); (3, 0.9). Beta subscript negative 1 is an inverse S-shaped curve that passes through the points (negative 3,1); (negative 1, 0.8); (0, 0.5); (1, 0.3); (3, 0).
A graph that illustrates the effect of varying values of β0 for the fixed value of [latex]\beta_1 = 1[/latex] on the mean response function [latex]\pi(X)[/latex] is given in Figure 3.32. As expected, the mean response function [latex]\pi(X)[/latex] is monotone increasing in all cases because [latex]\beta_1 > 1[/latex]. The effect of varying β0 is to shift the mean response functions horizontally. The rationale behind the horizontal shift can be seen by writing the mean response function with [latex]\beta_1 = 1[/latex] as
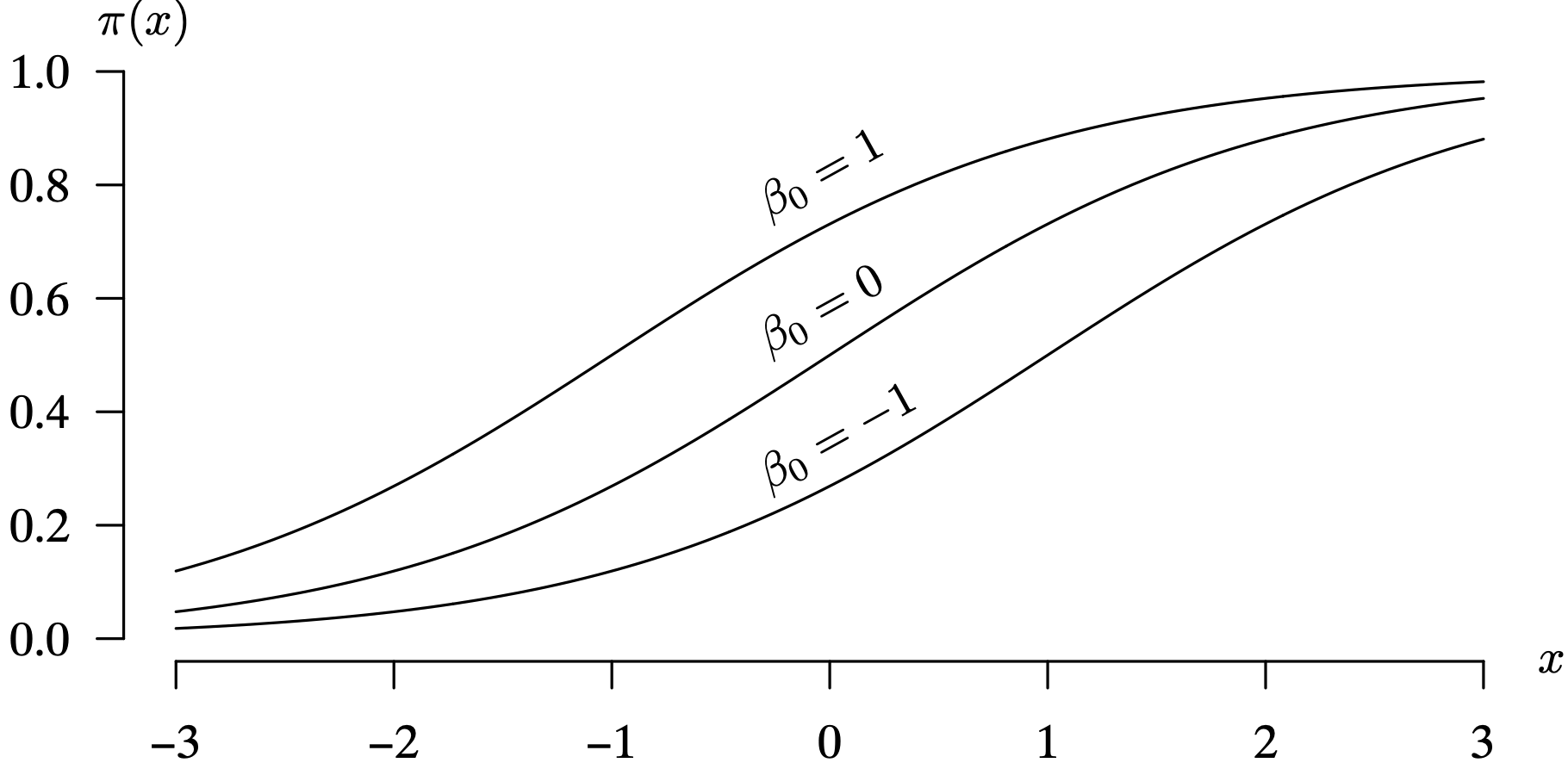
Long Description for Figure 3.32
The horizontal axis ranges from negative 3 to 3 in increments of 1. The vertical axis ranges from 0 to 1.0 in increments of 0.2. When Beta subscript 0 equals 1, the curve passes through the points (negative 3, 0.17); (negative 1, 0.4); (0, .7); (1, 0.8); (3,1). When beta subscript 0 equals 0, the curve passes through the points (negative 3, 0.12); (negative 1, 0.2); (0, 0.4); (1, 0.6); (3, 0.9). When beta subscript 0 equals negative 1, the curve passes through the points (negative 3, 0); (negative 1, 0.1); (0, 0.2); (1, 0.4); (3, 0.8). All data are approximate.
So the effect of increasing β0 in this case is to shift the mean response function to the right (for [latex]\beta_1 < 1[/latex]) or to the left (for [latex]\beta_1 > 1[/latex]) relative to the [latex]\pi(X)[/latex] curve associated with [latex]\beta_0 = 0[/latex].
To summarize, the sign of β1 controls the direction of the monotonicity of [latex]\pi(X)[/latex], the magnitude of β1 controls the steepness of [latex]\pi(X)[/latex], and β0 controls the location of [latex]\pi(X)[/latex] along the X-axis.
We now consider the estimation of the parameters β0 and β1 from a data set consisting of the n data pairs [latex](X_1, \, Y_1)[/latex], [latex](X_2, \, Y_2)[/latex], …, [latex](X_n, \, Y_n)[/latex]. The first components [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are real numbers and the second components [latex]Y_1, \, Y_2, \, \ldots, \, Y_n[/latex] assume only the values 0 and 1. Since
the contribution to the likelihood function of the data pair [latex](X_i, \, Y_i)[/latex] is
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. When [latex]Y_i = 0[/latex], the contribution to the likelihood function is [latex]1 - \pi(X_i)[/latex], which is [latex]P(Y_i = 0)[/latex], where [latex]P(Y_i = 0)[/latex] is the probability that [latex]Y_i = 0[/latex] for the particular setting of the independent variable at Xi. When [latex]Y_i = 1[/latex], the contribution to the likelihood function is [latex]\pi(X_i)[/latex], which is [latex]P(Y_i = 1)[/latex]. Since Xi is assumed to be observed without error, Yi is a random binary response, and the responses are assumed to be mutually independent random variables, the likelihood function is
The log likelihood function is
This can be written in terms of β0 and β1 as
or
The likelihood function and the log likelihood function are maximized at the same values of β0 and β1 because the natural logarithm is a monotonic transformation. The score vector is comprised of the partial derivatives of the log likelihood function with respect to β0 and β1:
and
When these two equations are equated to zero, there is no closed form solution for [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex], so numerical methods must be relied on to calculate these point estimates. The second derivatives of the log likelihood function after simplification are
and
The Fisher information matrix is the matrix of expected values of these partial derivatives:
The expected values in this matrix can be determined because they do not contain any random variables. Their values cannot be calculated, however, because the values of the parameters β0 and β1 are unknown. The observed information matrix
can be estimated from data values once the maximum likelihood estimators are computed. This matrix is the variance–covariance matrix of the score vector and its inverse is the asymptotic variance–covariance matrix of the maximum likelihood estimators. The square roots of the diagonal elements of this inverse matrix provide estimates of the standard errors of the maximum likelihood estimates.
The NFL field goal data set has a large sample size ([latex]n = 948[/latex]) and a strong statistical relationship between the length of the field goal attempt and the probability of success. The R code below again uses the optim function to calculate the parameter estimates. The first argument to optim are initial parameter estimates. The second argument to optim is the function to be minimized, so the negative of the log likelihood function is given as the second argument. Once the maximum likelihood estimates are calculated, the observed information matrix, standard errors, z-statistics, and associated p-values are calculated.

The results of the code are summarized in Table 3.10. The values of [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex] are both statistically significant with p-values near zero. The observed information matrix for the NFL field goal data set
|
i |
z |
p |
||
|---|---|---|---|---|
|
0 |
5.69 |
0.451 |
12.6 |
0.00 |
|
1 |
0.0106 |
0.00 |
is
These values can be compared to the values obtained using the glm (generalized linear model) function:

The results match those given in Table 3.10. When the link parameter within the binomial family is set to logit, the cumulative distribution function (or its complement) for the standard logistic distribution is employed. When the link parameter is set to probit, the cumulative distribution function (or its complement) for the standard normal distribution is employed. The logit and probit choices force the sigmoidal function to be symmetric, so that it approaches 0 and 1 at the same rate. When the link parameter is set to cloglog, the cumulative distribution function (or its complement) for the standard extreme value distribution is employed. It approaches 0 and 1 at the different rates.
When the following R statements are added to the code that generated Figure 3.28, the fitted mean response function [latex]\hat \pi(X)[/latex] is added to the graph.

The graph is shown in Figure 3.33. The estimated mean response function is monotone decreasing because [latex]\hat \beta_1 < 0[/latex] Furthermore, the mean response curve does an adequate job of modeling the probability of success as the points lie very close to the estimated mean response function. The estimated mean response function can be used for prediction. The estimated probability that a 38-yard field goal attempt is successful is
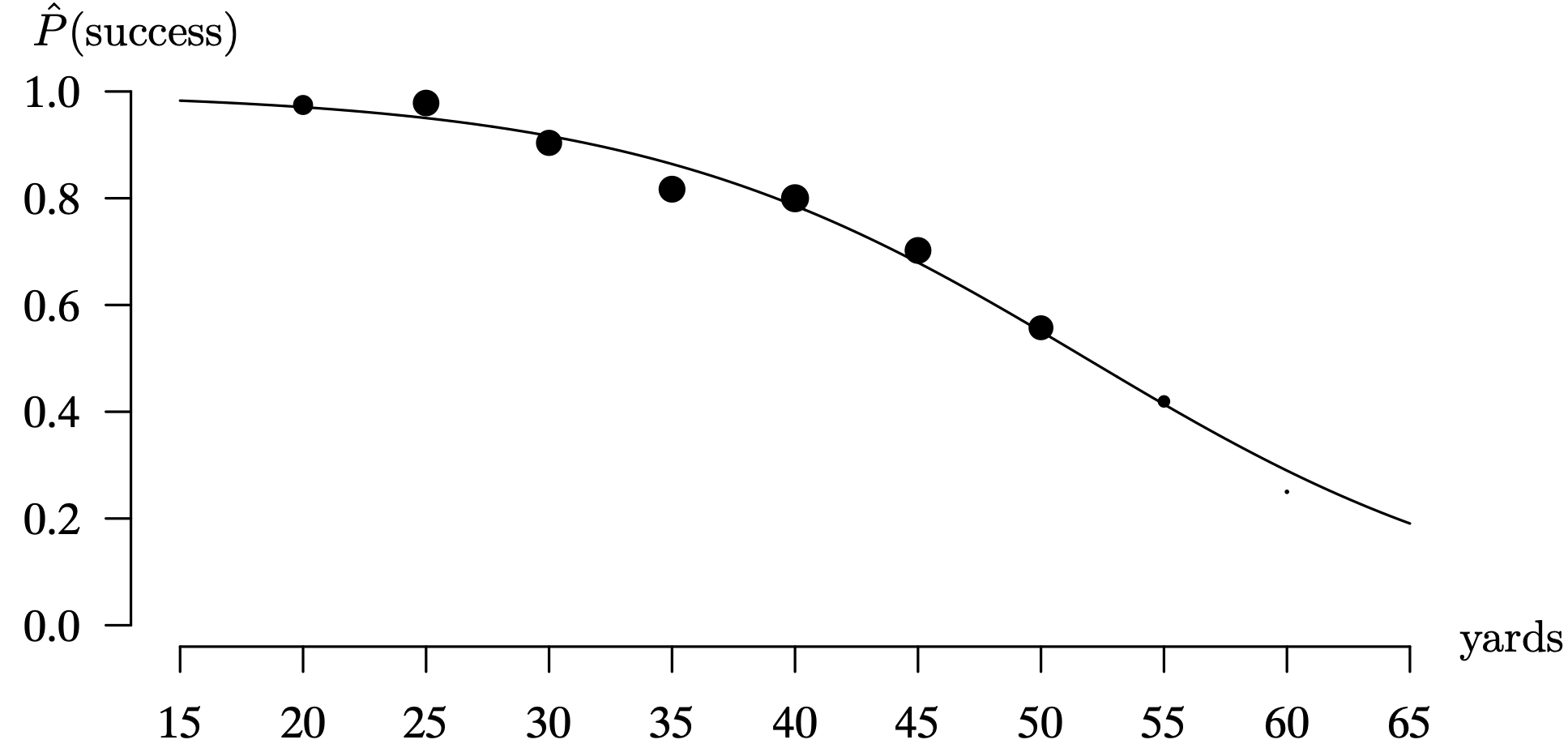
Long Description for Figure 3.33
The horizontal axis ranges from 15 to 65 in increments of 5. The vertical axis ranges from 0 to 1.0 in increments of 0.2. The datapoints plotted are as follows. (20, 1); (25,1); (30, 0.9); (35, 0.8);( 40, 0.8); (45, 0.7); (50, 0.6); (55, 0.4). A curve passing through all of the plotted points expect (35, 0.8), follows a decreasing trend.
This value can be generated with the predict function in R with the additional statements
Some keystrokes can be saved by using the type = “response” argument in the call to predict.
The limitations of a symmetric mean response function also become apparent in this case. The estimated probability that a 71-yard field goal attempt is successful is
even though the NFL field goal record from 2021 is 66 yards. This is clearly a case of extrapolating beyond the range of the data, which is discouraged. The meaningful range of [latex]\hat \pi (X)[/latex] is over the scope of the model [latex]18 \le X \le 62[/latex], whose endpoints are the shortest and longest field goal attempt during the 2003 season. The symmetric nature of the logistic distribution makes the [latex]\hat \pi (X)[/latex] values associated with X-values greater than 62 yards higher than are meaningful.
Confidence intervals for the parameters in a logistic regression model can be calculated with the confint and confint.default functions. These confidence intervals give a measure of the precision of the point estimates. The R code below calculates the 95% confidence intervals for the parameters using the confint and confint.default functions for the NFL field goal data.

The first set of confidence intervals that are returned via confint use the profiled log likelihood function to return the confidence intervals given in the output below. The default is a 95% confidence interval.

To three significant digits, these 95% confidence intervals are
The second set of confidence intervals that are returned via confint.default are based on the asymptotic normality of the maximum likelihood estimators. The call to confint.default returns the confidence intervals given in the output below.

To three significant digits, these 95% confidence intervals are
Alternatively, the 95% confidence interval for β1 can be calculated by using the qnorm function to calculate the appropriate quantile from the standard normal distribution.

The 95% confidence interval for β1 that is returned matches that returned by confint.default. The confidence intervals based on the asymptotic normality of the maximum likelihood estimator from confint.default will be symmetric about the maximum likelihood estimators, but the confidence interval based on the profiled log likelihood function from confint will not be symmetric about the maximum likelihood estimators. The confidence intervals given here are somewhat narrow because of the large sample size of [latex]n = 948[/latex] for the NFL field goal data.
The last topic is the interpretation of the point estimators for the coefficients. This interpretation is much more difficult than the interpretation of the coefficients in a standard simple linear regression model. The next paragraph defines the odds and the log odds. The subsequent paragraph relates the log odds to the logistic regression model.
Consider an event which occurs with probability 0.9. The probability that the event will not occur is 0.1. The odds are defined as the ratio of the probability that the event will occur to the probability that the event will not occur. In this case that ratio is 9, so the odds are often referred to as 9 to 1. Table 3.11 gives several probability values and associated odds for several probability values.
|
Probability |
Odds |
|---|---|
|
0.2 |
0.25 |
|
0.5 |
1 |
|
0.6 |
1.5 |
|
0.75 |
3 |
|
0.8 |
4 |
|
0.9 |
9 |
|
0.99 |
99 |
The R code below generates a graph of the odds on the vertical axis versus the probability on the horizontal axis.
Figure 3.34 shows the transformation from probability to odds, which reveals a monotone increasing function. Probabilities fall on the interval [latex][0, \, 1][/latex]; odds fall on the interval [latex][0, \, \infty )[/latex]. The natural logarithm of the odds is the function, known as the log odds, which is a transformation of the probability p in the following fashion:
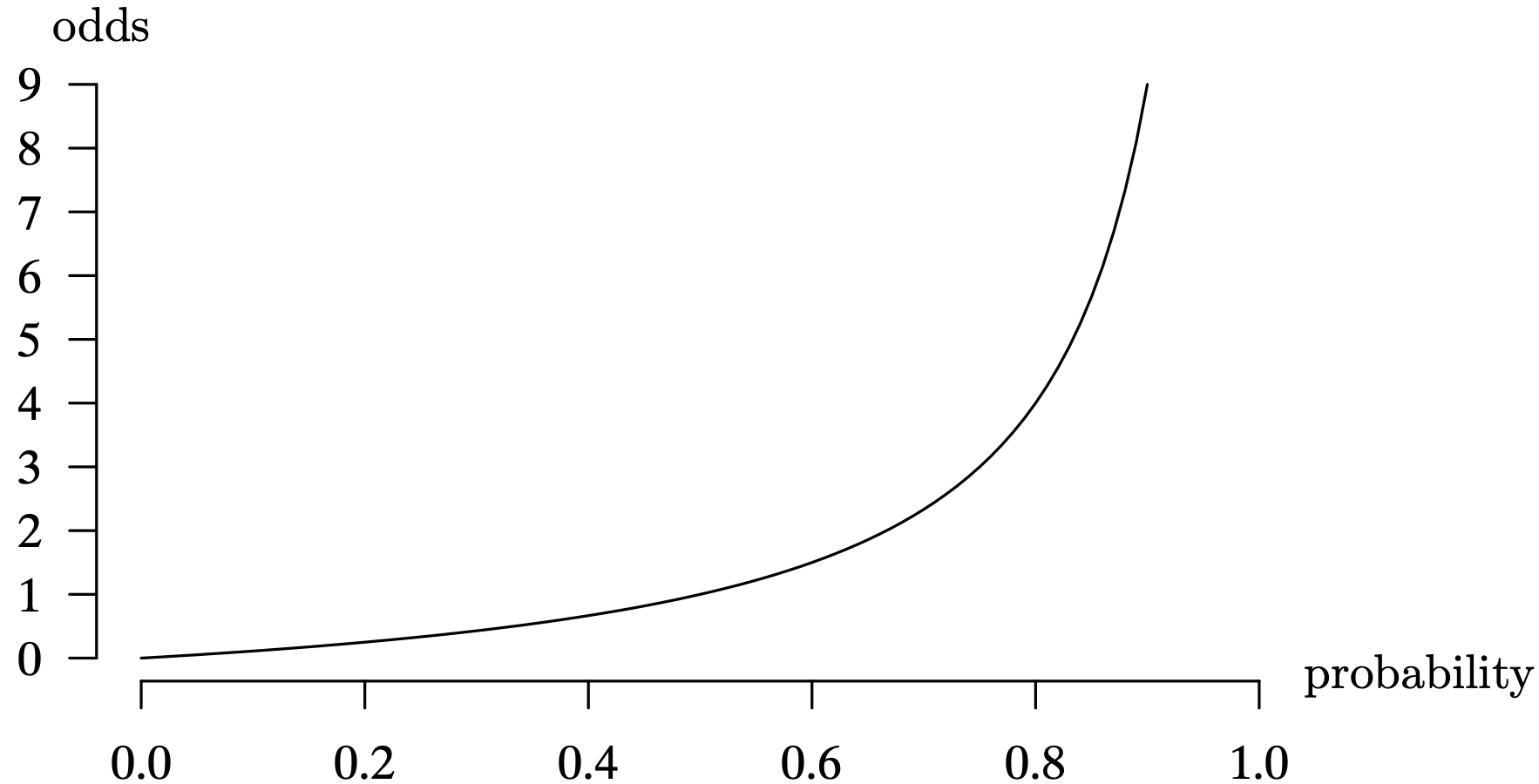
Long Description for Figure 3.34
The horizontal axis measuring probability, ranges from 0 to 1 in increments of 0.2. The vertical axis measuring odds ranges from 0 to 9 in increments of 1. A curve following an increasing trend passes through the points (0.0, 0); (0.2, 0.5); (0.4, 1); (0.6, 1.5); (0.8, 2.5); and (0.9, 9).
This is a transformation from [latex][0, \, 1][/latex] to [latex]( - \infty, \, \infty )[/latex]. Table 3.12 extends the previous table by including a column for the log odds. Notice that a probability of [latex]1 / 2[/latex] corresponds to a log odds of 0 and the symmetry of the log odds associated with the probabilities 0.2 and 0.8. The R code below graphs the log odds versus the probability.
|
Probability |
Odds |
Log Odds |
|---|---|---|
|
0.2 |
0.25 |
|
|
0.5 |
1 |
0 |
|
0.6 |
1.5 |
0.4055 |
|
0.75 |
3 |
1.0986 |
|
0.8 |
4 |
1.3863 |
|
0.9 |
9 |
2.1972 |
|
0.99 |
99 |
4.5951 |

The associated graph is shown in Figure 3.35. The shape of the log odds is a transformed version of the mean response functions seen earlier. The purpose of defining the log odds is to convert from probability, which has a restricted range between 0 and 1, and the log odds, which has an unrestricted range.
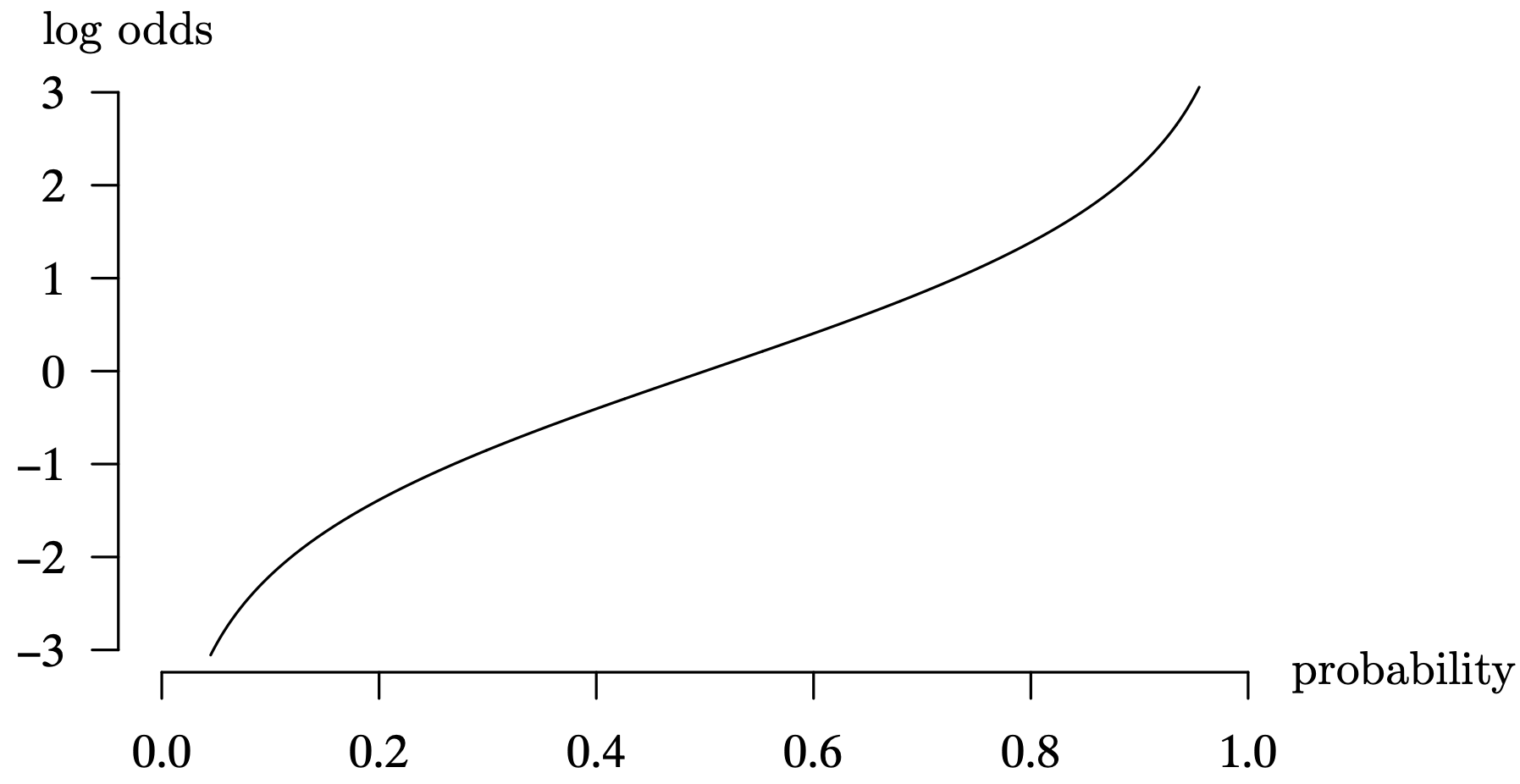
Long Description for Figure 3.35
The horizontal axis measuring probability, ranges from 0 to 1 in increments of 0.2. The vertical axis measuring log odds ranges from negative 3 to 3 in increments of 1. A curve passes through the points as follows. (0.0, negative 3); (0.2, negative 1.5); (0.4, negative 0.5); (0.6, .5); (0.8, 1.5); (1.0, 3). The curve increases until 0.4, inflects at 0.5, and increases steadily to the right of the quadrant.
Now back to logistic regression and the interpretation of the estimated coefficients. Recall that for a simple logistic regression problem, the mean response function is
where x is the independent variable and Y is the response variable. The logit transformation of [latex]\pi(x)[/latex] is
Since [latex]\pi(x)[/latex] is a probability, the expression on the left-hand side of this equation is a log odds.
Now consider the NFL data. From the earlier work, the estimated intercept provided by the R glm function is [latex]\hat \beta_0 = 5.6979[/latex] and the estimated coefficient associated with the length of the field goal attempt in yards is [latex]\hat \beta_1 = -0.1099[/latex]. The estimated intercept is the log odds of a kicker making a field goal from a (theoretical) zero yards, which has no meaningful interpretation in this setting. The value of [latex]\hat \beta_1 = -0.1099[/latex] is the change in the log odds for a one-yard change in the length of the field goal attempt. Additionally, the quantity
is the multiplier that gives the change in the odds for a one-unit change in the independent variable. We expect to see a 10.4% decrease in the odds associated with the probability of success for a field goal attempt for every additional yard added to the field goal attempt. This value and an associated 95% confidence interval can be generated with the additional R statement

The analysis of the NFL data given here is a composite of all kickers in the NFL during 2003. Individual kickers within the NFL will have their own logistic regression curve.
With this background concerning simple logistic regression in place, it is straightforward to extend this to more complicated modeling situations. Additional topics in logistic regression include constructing a confidence interval for a predicted value, the calculation of deviance residuals, including multiple independent variables in a logistic regression model, model assessment, and interpreting estimated coefficients for interaction terms.
3.9 Exercises
-
-
3.1 Write a paragraph that describes why the sum of squares for error associated with the simple linear regression model [latex]Y = \beta_0 + \beta_1 X + \epsilon[/latex] will always be less than or equal to the sum of squares for error associated with the simple linear regression model forced through the origin [latex]Y = \beta_1 X + \epsilon[/latex] for the same data pairs [latex]\left( X_1, \, Y_1 \right), \, \left( X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex].
-
3.2 Under what condition(s) does the regression line forced through the origin have the same sum of squares for error as the simple linear regression for the full model [latex]Y = \beta_0 + \beta_1 X + \epsilon[/latex] for the same data pairs [latex]\left( X_1, \, Y_1 \right), \, \left( X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex].
-
3.3 Consider the simple linear regression model forced through the origin
Show that the least squares estimator [latex]\hat \beta_1[/latex] is an unbiased estimator of β1.
-
3.4 Consider the simple linear regression model forced through the origin
Find [latex]V \big[ \hat \beta_1 \big][/latex].
-
3.5 Consider the simple linear regression model forced through the origin with normal error terms,
where [latex]\epsilon \sim N\left( 0, \, \sigma ^ {\, 2} \right)[/latex].
- Find the maximum likelihood estimators of β1 and σ2.
- Show that the maximum likelihood estimators maximize the log likelihood function.
-
3.6 Give an example of [latex]n = 2[/latex] data pairs corresponding to the case in which a simple linear regression line forced through the origin contains the point [latex]\left( \bar X , \, \bar Y \right)[/latex].
-
3.7 Give an example of [latex]n = 2[/latex] data pairs corresponding to the case in which a simple linear regression line forced through the origin does not contain the point [latex]\left( \bar X , \, \bar Y \right)[/latex].
-
3.8 Consider the simple linear regression model forced through the origin with normal error terms
with known parameters β1 and σ2. Find an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for β1 from n data pairs [latex]\left( X_1, \, Y_1 \right), \, \left( X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex].
-
3.9 Consider the simple linear regression model forced through the origin with normal error terms,
with unknown parameters β1 and σ2. Show that the R statement
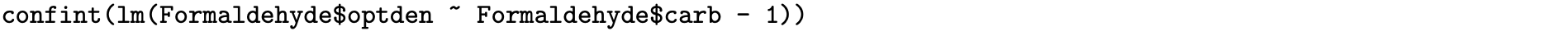
uses the formula
to calculate the 95% two-sided confidence interval for β1 for the data pairs in the built-in R data frame Formaldehyde. Notice that the degrees of freedom are one more than the associated degrees of freedom for the full simple linear regression model.
-
-
3.10 Consider the simple linear regression model forced through the origin with normal error terms,
with unknown parameters β1 and σ2. Conduct a Monte Carlo simulation experiment to provide convincing numerical evidence that the two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval
is an exact confidence interval for β1 for the following parameter settings: [latex]n = 3[/latex], [latex]\alpha =0.05[/latex], [latex]\beta_1 = 2[/latex], [latex]X_1 = 1[/latex], [latex]X_2 = 2[/latex], [latex]X_3 = 3[/latex], and [latex]\sigma ^ {\, 2} = 1[/latex].
-
3.11 The Brown–Forsythe test can be used to determine whether the error terms have constant variance. In particular, it tests for equality of the variances of the error terms in two subsets of the data values. The test is analogous to a t-test. The test is robust with respect to departures from normality of the error terms. The data pairs are partitioned by a threshold value of X which is not one of the [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] values. Let n1 be the number of data pairs with X-values less than the threshold value and n2 be the number of data pairs with X-values greater than the threshold value so that [latex]n = n_1 + n_2[/latex]. In addition, let
- [latex]e_{i1}[/latex] be residual i for group 1,
- [latex]e_{i2}[/latex] be residual i for group 2,
- [latex]\tilde e_1[/latex] be the sample median of the group 1 residuals,
- [latex]\tilde e_2[/latex] be the sample median of the group 2 residuals,
- [latex]d_{i1} = |e_{i1} - \tilde e_1|[/latex],
- [latex]d_{i2} = |e_{i2} - \tilde e_2|[/latex],
- [latex]\bar d_{1} = (1 / n_1) \sum_{i\,=\,1}^{n_1} d_{i1}[/latex], and
- [latex]\bar d_{2} = (1 / n_2) \sum_{i\,=\,1}^{n_2} d_{i2}[/latex].
The test statistic for the Brown–Forsythe test is
where s2 is the pooled sample variance
The test statistic is approximately [latex]t(n - 2)[/latex] when the population variances of the error terms in the two groups are equal n1 and n2 are large enough so that the dependency between the residuals is not too large. Write R code to compute the p-value for the Brown–Forsythe test for the cars data set using speed as the independent variable and dist as the dependent variable with a threshold value of 13.5 miles per hour.
-
3.12 Find the leverages for [latex]n = 2[/latex] data pairs in a simple linear regression model.
-
3.13 For a simple linear regression model with [latex]X_i = i[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], derive a formula for the leverage of the ith data pair.
-
3.14 Write R functions named cooks.distance1, cooks.distance2, and cooks.distance3, which calculate the Cook's distances for each of the n data pairs associated with the simple linear regression model
using the three formulas from Definition 3.3. The arguments for these three functions are the vector x, which contains the n values of the independent variable, and the vector y, which contains the n values of the dependent variable. Test your functions on the Formaldehyde data set which is built into R, with carb as the independent variable and optden as the dependent variable.
-
3.15 Make a scatterplot (with associated regression line) of the [latex]n = 11[/latex] data pairs in the third data set in Anscombe's quartet with the R commands
Without doing any calculations,
- circle the point(s) with the largest leverage, and
- circle the point(s) with the largest Cook's distance.
-
3.16 What is the smallest and largest possible leverage?
-
3.17 Show that leverage is scale invariant. In other words, show that the leverages remain unchanged when the scale of the independent variable changes (for example, from centimeters to meters).
-
3.18 Use Monte Carlo simulation to estimate the probability that all of the Cook's distances are less than 1 for a simple linear regression model with normal error terms and the following parameter settings: [latex]\beta_0 = 1[/latex], [latex]\beta_1 = 1 / 2[/latex], [latex]\sigma = 1[/latex], [latex]n = 10[/latex], and [latex]X_i = i[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. Is this probability affected by changes is σ or n?
-
3.19 Use Monte Carlo simulation to draw empirical cumulative distribution functions of Cook's distances D1, D2, D3, D4, and D5 for a simple linear regression model with the following parameter settings: [latex]\beta_0 = 1[/latex], [latex]\beta_1 = 1 / 2[/latex], [latex]\sigma = 1[/latex], [latex]n = 10[/latex], and [latex]X_i = i[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
-
3.20 Consider a simple linear regression model with the independent variable X and the dependent variable Y having the same units (for example, centimeters). If the same linear transformation is applied to both X and Y so as to change their units (for example, from centimeters to meters), show that the Cook's distances remain unchanged.
-
3.21 Show that the row sums of the hat matrix are all equal to 1 for data pairs [latex]\left( X_1, \, Y_1 \right)[/latex], [latex]\left( X_2, \, Y_2 \right)[/latex], [latex]\ldots \,[/latex], [latex]\left( X_n, \, Y_n \right)[/latex] in a simple linear regression model.
-
3.22 Perform a Monte Carlo simulation to provide convincing numerical evidence that
for a simple linear regression model with normal error terms of your choice. This result is used to establish a [latex]{100(1 - \alpha)}\%[/latex] confidence region for β0 and β1.
-
3.23 Show that the residuals [latex]e_i = Y_i - \hat{Y}_i[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], can be written in terms of the hat matrix [latex]{\bf H}[/latex] as
-
3.24 For the simple linear regression model with normal error terms, the variance–covariance matrix of [latex]\hat{\pmb{\beta}}[/latex] is
For data pairs [latex]\left( X_1, \, Y_1 \right), \, \left(X_2, \, Y_2 \right), \, \ldots , \, \left( X_n, \, Y_n \right)[/latex], give an estimator for this matrix.
-
3.25 For the simple linear regression model, show that
-
3.26 For a simple linear regression model, show that the matrix equation
where
corresponds to the normal equations given in Theorem 1.1 as
-
[latex]\begin{align*} n \hat \beta_0 + \hat \beta_1 \sum_{i\,=\,1}^n X_i & = \sum_{i\,=\,1}^n Y_i \\ \hat \beta_0 \sum_{i\,=\,1}^n X_i + \hat \beta_1 \sum_{i\,=\,1}^n X_i ^ 2 & = \sum_{i\,=\,1}^n X_i Y_i. \end{align*}[/latex]
-
3.27 A multiple linear regression model is used to determine the relationship between the sales price of a home Y as a function of the two predictor variables: X1, the number of square feet in the home, and X2, the distance from downtown in miles. The fitted model is
One home sells for $314,159. Find the predicted sales price for a second home, which is the same size as the first but is ten miles further away from downtown that the first home.
-
3.28 The R built-in data frame named swiss contains a standardized fertility measure and five socio-economic indicators for 47 French-speaking provinces in Switzerland from about 1888.
- Using a forward stepwise regression with threshold [latex]\alpha = 0.05[/latex], determine a multiple linear regression model with a dependent variable Y, the standardized fertility measure, and the five associated potential independent variables.
- Using a backward stepwise regression with threshold [latex]\alpha = 0.05[/latex], determine a multiple linear regression model with a dependent variable Y, the standardized fertility measure, and the five associated potential independent variables.
- For one of the two final multiple linear regression models determined in parts (a) and (b), test the statistical significance of all possible interaction terms.
-
3.29 Show that when the independent variables X1 and X2 in a multiple linear regression model are uncorrelated, the estimator for [latex]\hat \beta_1[/latex] is the same for both the simple linear regression model involving just X1 and Y and the multiple linear regression model involving X1, X2, and Y.
-
3.30 Consider a simple linear regression model that uses the weighted least squares estimation. When all of the weights [latex]w_1, \, w_2, \, \ldots, \, w_n[/latex] are equal, show that the weighted least squares normal equations reduce to the associated unweighted least squares normal equations.
-
3.31 “I first believed I was dreaming …but it is absolutely certain and exact that the ratio which exists between the period times of any two planets is precisely the ratio of the 3/2th power of the mean distance” was the reaction of Johannes Kepler upon discovering the relationship
as translated from Harmonies of the World by Kepler in 1619, where x is the distance between a planet and the sun and y is the period. Using the data from the Wikipedia webpage titled Kepler's Laws of Planetary Motion, the data values for the [latex]n = 8[/latex] planets are given below.
Planet
Semi-major axis (AU) x
Period (days) y
Mercury
0.38710
87.9693
Venus
0.72333
224.7008
Earth
1
365.2564
Mars
1.52366
686.9796
Jupiter
5.20336
4332.8201
Saturn
9.53707
10,775.599
Uranus
19.1913
30,687.153
Neptune
30.0690
60,190.03
The semi-major axes values are measured in Astronomical Units (AU).
- Make an appropriate scatterplot to visually assess whether a regression model is appropriate.
- Find the least squares point estimate for β.
- Perhaps fit a least squares model in another fashion.
- Interpret the value for [latex]\hat \beta[/latex].
- Find a 95% confidence interval for β.
-
3.32 Fit the quadratic regression function forced through the origin
to the data pairs in the cars data frame in R, where X is the speed of the car in miles per hour and Y is the stopping distance in feet.
-
3.33 Using an extreme value distribution as a link function, fit a regression function to the 2003 NFL field goal data from Section 3.8 and use the fitted model to predict that probability of success on a 38-yard field goal attempt.

