Chapter 5 Statistical Methods in Survival Analysis
The previous chapter introduced probability models that are frequently used in survival analysis. This chapter introduces the associated statistical methods.
The focus in this chapter is the use of maximum likelihood for parameter estimation and inference. Likelihood theory is illustrated in the first section. The matrix of the expected values of the opposite of the second partial derivatives of the log likelihood function is known as the Fisher information matrix and its statistical analog, the observed information matrix, is useful for determining confidence intervals for parameters. Asymptotic properties of the likelihood function, which are associated with large sample sizes, are reviewed in the second section. One distinctive feature of lifetime data is the presence of censoring, which occurs when only an upper or lower bound on the lifetime is known. Statistical methods for handling censored data values are introduced in the third section. The focus is on right censoring, where only a lower bound on the failure time is known. These methods are applied to the exponential distribution and the Weibull distribution in the next two sections. Finally, the last section indicates how to fit the proportional hazards model to a data set consisting of lifetimes with associated covariates.
5.1 Likelihood Theory
There are always merits in obtaining raw data (that is, exact individual failure times), as opposed to grouped data (counts of the number of failures over prescribed time intervals). Given raw data, we can always construct grouped data, but the converse is typically not true; therefore, we limit discussion in this chapter to the raw data case.
The random variable T has denoted a random lifetime in previous chapter. So it is natural to use [latex]T_1, \, T_2, \, \ldots, \, T_n[/latex] to denote a random sample of n such lifetimes, where n is the number of items on test. When specific values are given for realizations of such lifetimes, which is typically the case from this point forward, they are denoted by [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex]. In other words, [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] are the experimental values of the mutually independent and identically distributed random variables [latex]T_1, \, T_2, \, \ldots, \, T_n[/latex]. The associated ordered observations, or order statistics, are denoted by [latex]t_{(1)}, \, t_{(2)}, \, \ldots, \, t_{(n)}[/latex].
The Greek letter θ is often used to denote a generic unknown parameter. We will refer to [latex]\hat \theta[/latex] in the abstract as a point estimator; when [latex]\hat \theta[/latex] assumes a specific numeric value, it will be referred to as a point estimate. The probability distribution of a statistic is referred to as a sampling distribution.
Assume that there is a single unknown parameter θ in the probability model for T. Assume further that the data values [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] are mutually independent and identically distributed random variables. The joint probability density function of the data values is the product of the marginal probability density functions of the individual observations:
This function is the likelihood function. In order to simplify the notation, the likelihood function is often written as simply
The maximum likelihood estimator of θ, which is denoted by [latex]\hat \theta[/latex], is the value of θ that maximizes [latex]L(\theta)[/latex].
The next example reviews the associated notions of the log likelihood function, score vector, maximum likelihood estimator, Fisher information matrix, and observed information matrix for a two-parameter lifetime model. We assume for now that there are no censored observations in the data set; all of the failure times are observed.
In some cases, it is possible to find the exact distribution of a pivotal quantity which results in exact statistical inference (that is, constructing exact confidence intervals and performing exact hypothesis tests). It is more often the case that exact statistical inference is not possible, and asymptotic properties associated with the likelihood function must be relied on for approximate inference. The next section reviews some asymptotic properties that arise in likelihood theory. When a large data set of lifetimes is available, these properties often lead to approximate statistical methods of inference.
5.2 Asymptotic Properties
When the number of items on test n is large, there are some asymptotic results concerning the likelihood function that are useful for constructing confidence intervals and performing hypothesis tests associated with a vector of p unknown parameters [latex]\boldsymbol{\theta} = \left( \theta_1 , \, \theta_2 , \, \ldots , \, \theta_p \right) ^ \prime[/latex]. As indicated in the example in the last section, the [latex]p \times 1[/latex] score vector [latex]{\boldsymbol U} (\boldsymbol{\theta})[/latex] has elements
for [latex]i = 1, \, 2, \, \ldots, \, p[/latex]. Therefore, each element of the score vector is a sum of mutually independent random variables, and, when n is large, the elements of [latex]\boldsymbol{U}( \boldsymbol{\theta})[/latex] are asymptotically normally distributed by the central limit theorem. More specifically, the score vector [latex]\boldsymbol{U} (\boldsymbol{\theta})[/latex] is asymptotically normal with population mean [latex]{\bf 0}[/latex] and variance–covariance matrix [latex]I(\boldsymbol{\theta})[/latex], where [latex]I(\boldsymbol{\theta})[/latex] is the Fisher information matrix. This means that when the true value for the parameter vector is [latex]\boldsymbol{\theta}_0[/latex] then
is asymptotically chi-square with p degrees of freedom. This can be used to determine confidence intervals and perform hypothesis tests with respect to [latex]\boldsymbol{\theta}[/latex].
The maximum likelihood estimator for the parameter vector [latex]\hat{\boldsymbol{\theta}}[/latex] can also be used for confidence intervals and hypothesis testing. Since [latex]\hat{\boldsymbol{\theta}}[/latex] is asymptotically normal with population mean [latex]\boldsymbol{\theta}[/latex] and variance–covariance matrix [latex]I^{-1} (\boldsymbol{\theta})[/latex], when [latex]\boldsymbol{\theta} = \boldsymbol{\theta}_0[/latex],
is also asymptotically chi-square with p degrees of freedom. Two statistics that are asymptotically equivalent to this statistic that can be used to estimate the value of the chi-square random variable are
and
A third asymptotic result involves the likelihood ratio statistic
which is asymptotically chi-square with p degrees of freedom. The conditions necessary for these asymptotic properties to apply are cited at the end of the chapter.
These three asymptotic results are summarized in the result below, where the a above the ∼ is shorthand for “asymptotically distributed.”
All of the statistical methods developed thus far have assumed that we are able to observe all n of the items on test fail. The associated lifetimes are denoted by [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex]. Although this is ideal and might be the case in some settings, a short testing time or items with long lifetimes might result in some items that survive the test. The lifetimes of the items which do not fail during the test are known as right-censored observations. The lifetimes of these items are not observed, but are known to exceed the time at which the test is concluded. If a decision concerning the acceptability of the items must be made with some of the items still operating at the end of the test, then a statistical model must be formulated to account for the unobserved lifetimes of these items. The next section introduces the important topic of censoring, which is pervasive in survival analysis.
5.3 Censoring
Censoring occurs in lifetime data sets when only an upper or lower bound on the lifetime is known. Censoring occurs frequently in lifetime data sets because it is often impossible or impractical to observe the lifetimes of all the items on test. A data set for which all failure times are known is called a complete data set. Figure 5.1 illustrates a complete data set of [latex]n = 5[/latex] items placed on test simultaneously at time [latex]t = 0[/latex], where the [latex]\times[/latex]'s denote failure times. Consider the two endpoints of each of the horizontal segments. It is critical to provide an unambiguous definition of the time origin (for example, the time a product is purchased or the time a cancer is diagnosed). Likewise, failure must be defined in an unambiguous fashion. This is easier to define for a light bulb or a fuse than for a ball bearing or a sock. Outside of a reliability setting, a data set of lifetimes is often generically referred to as time-to-event data, corresponding to the time between the time origin and the event of interest. A censored observation occurs when only a bound is known on the time of failure. If a data set contains one or more censored observations, it is called a censored data set.
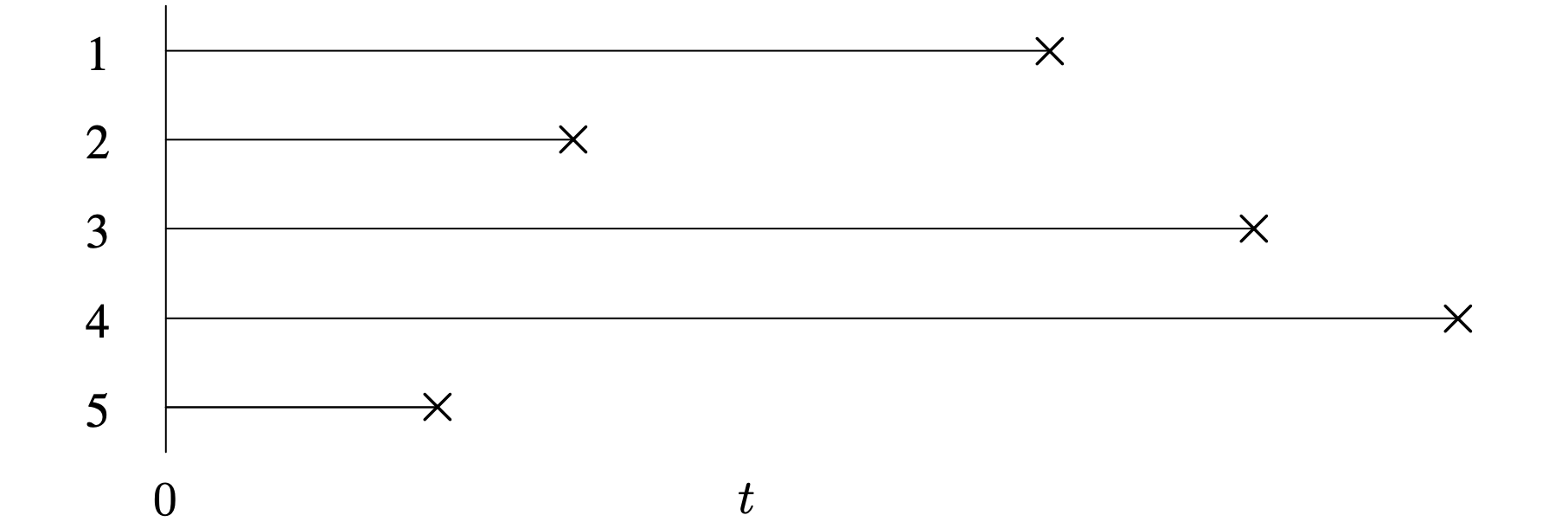
Long Description for Figure 5.1
The horizontal axis measures time t and has the initial time t equals 0. The vertical axis represents the number of items 1 through 5 from top to bottom. The time to event data is shown as horizontal line segments of different lengths from the vertical axis with X marks at the other end. The X marks indicate the failure times. All line segments are drawn from t equals 0. Item 4 has a maximum number of failures, followed by items 3, 1, 2, and 5, in that order.
The most common type of censoring is known as right censoring. In a right-censored data set, one or more items have only a lower bound known on their lifetime. The term sample size is now vague. From this point forward, we use n to denote the number of items on test and use r to denote the number of observed failures. In an industrial life testing situation, for example, [latex]n = 12[/latex] cell phones are put on a continuous, rigorous life test on January 1, and [latex]r = 3[/latex] of the cell phones have failed by December 31. These failed cell phones are discarded upon failure. The remaining [latex]n - r = 12 - 3 = 9[/latex] cell phones that are still operating on December 31 have lifetimes that exceed 365 days, and are therefore right-censored observations. Right censoring is not limited to just reliability applications. In a medical study in which T is the survival time after the diagnosis of a particular type of cancer, for example, a patient can either (a) still be alive at the end of a study, (b) die of a cause other than the particular type of cancer, constituting a right-censored observation, or (c) lose contact with the study (for example, if they leave town), constituting a right-censored observation.
Three special cases of right censoring are common in survival analysis. The first is Type II or order statistic censoring. As shown in Figure 5.2, this corresponds to terminating a study upon one of the ordered failures. The diagram corresponds to a set of [latex]n = 5[/latex] items placed on a test simultaneously at time [latex]t = 0[/latex]. The test is terminated when [latex]r = 3[/latex] failures are observed. Time advances from left to right in Figure 5.2 and the failure of the first item (corresponding to the third ordered observed failure) terminates the test. The lifetimes of the third and fourth items are right censored. Observed failure times are indicated by an [latex]{\large{\times}}[/latex] and right-censoring times are indicated by a [latex]\, \Large{\circ}[/latex]. In Type II censoring, the time to complete the test is random.
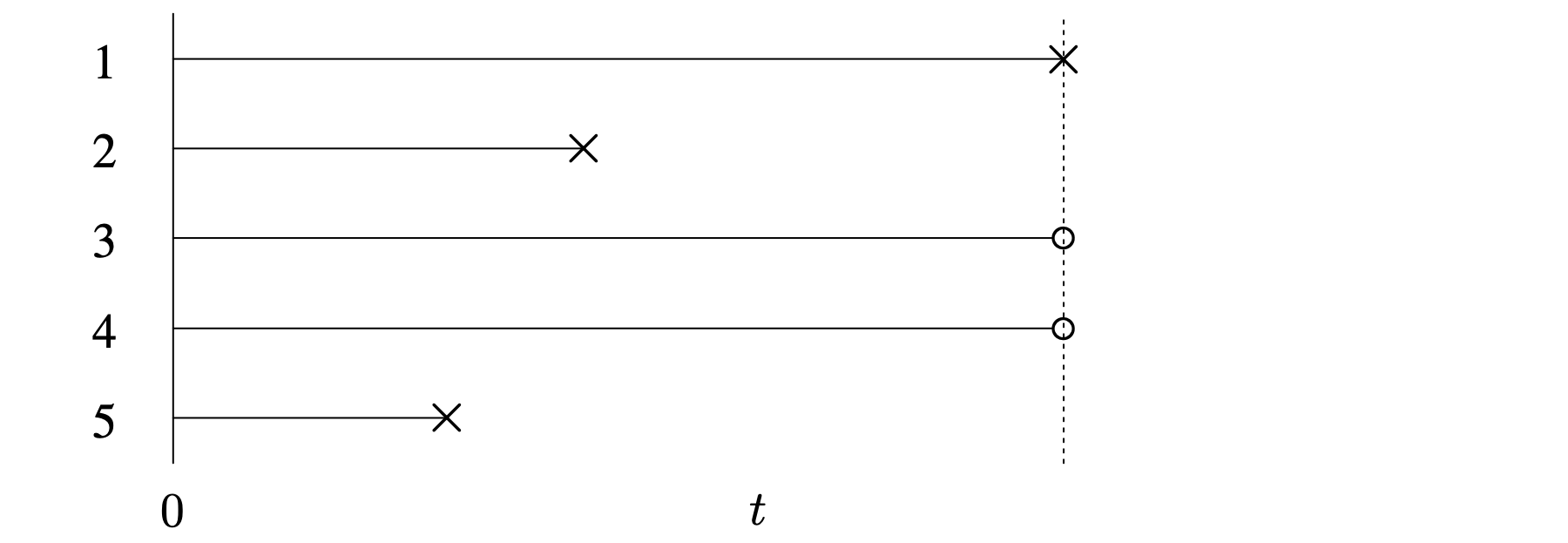
Long Description for Figure 5.2
The horizontal axis measures time t and has the initial time t equals 0. The vertical axis represents the number of items 1 through 5 from top to bottom. All horizontal line segments are drawn from t equals 0. Line segments of different lengths are represented with an X mark and a circle at the other end. The X marks indicate the failure times and the circles denote censoring times. Items 1, 3, and 4 have equal maximum failure times, and item 5 has a short failure time. The lifetimes of the third and fourth items are right censored. The termination times of items 1, 3, and 4 are connected by a dotted vertical line.
The second special case is Type I or time censoring. As shown in Figure 5.3, this corresponds to terminating the study at a particular time. The diagram shows a set of [latex]n = 5[/latex] items placed on a test simultaneously at [latex]t = 0[/latex] that is terminated at the time indicated by the dotted vertical line. For the realization illustrated in Figure 5.3, there are [latex]r = 4[/latex] observed failures. In Type I censoring, the number of failures r is random.
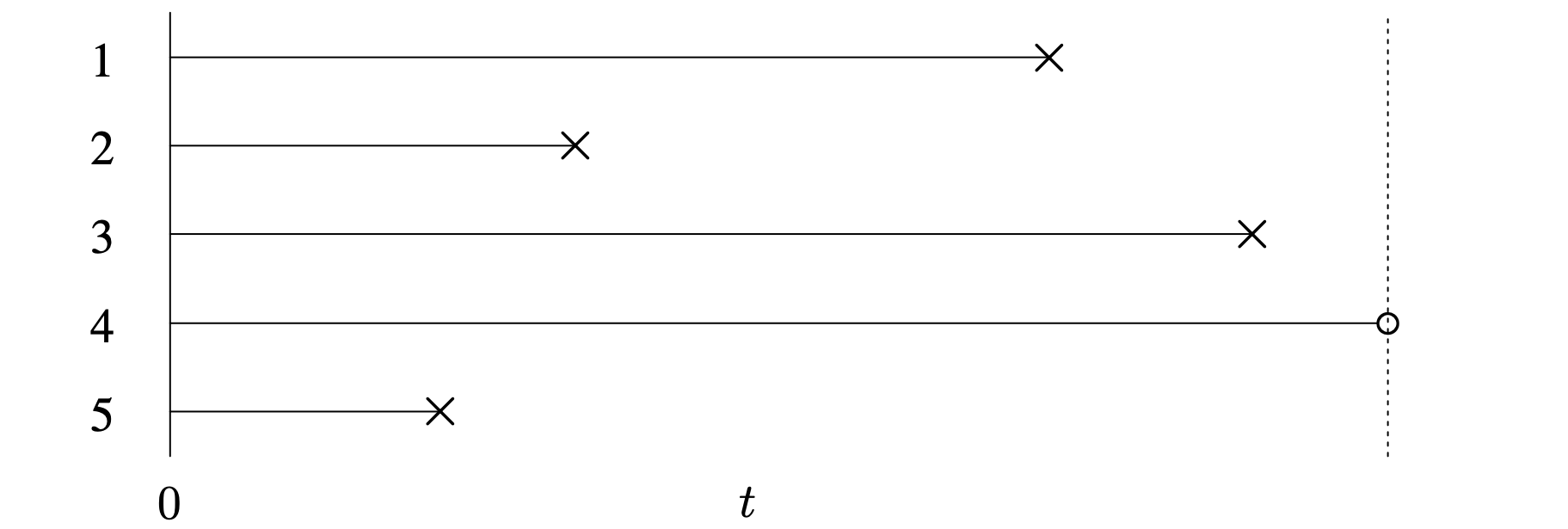
Long Description for Figure 5.3
The horizontal axis measures time t and has the initial time t equals 0. The vertical axis represents the number of items 1 through 5, from top to bottom. All horizontal line segments are drawn from t equals 0. Line segments of different lengths are marked with X marks and circles at the other end. The X marks indicate the failure times and the circles indicate censoring times Item 4 has a maximum lifetime, next comes, items 3, 1, 2, and 5. Among these, item 4 is right censored. A dotted vertical line is drawn on the termination of item 4.
Finally, random censoring occurs when individual items are withdrawn from the test at any time during the study. Figure 5.4 illustrates a realization of a randomly right-censored life test with [latex]n = 5[/latex] items on test and [latex]r = 2[/latex] observed failures. It is usually assumed that the failure times and the censoring times are mutually independent random variables and that the probability distribution of the censoring times does not involve any unknown parameters from the failure time distribution. In other words, in a randomly censored data set, items cannot be more or less likely to be censored because they are at unusually high or low risk of failure.
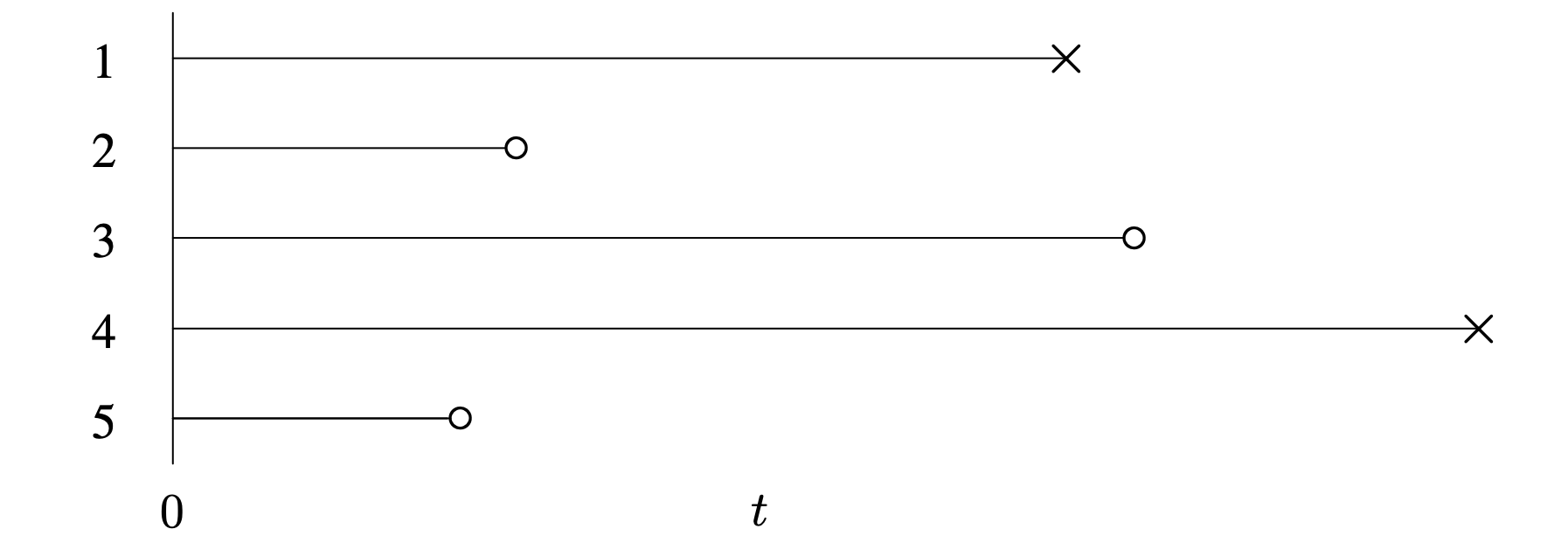
Long Description for Figure 5.4
The horizontal axis measures time t and has the initial time t equals 0. The vertical axis represents the number of items 1 through 5 from top to bottom. All horizontal line segments begin at the same time t equals 0. Horizontal line segments of different lengths are marked with X marks or circles at the other end. The X marks indicate the failure times and the circles denote censoring times. Item 4 has maximum lifetime, next comes, items 3, 1, 2, and 5. Among these, items 2, 3, and 5 are right censored.
Although other types of censoring exist, such as left censoring and interval censoring, the focus of this chapter will be on right censoring because it is the most common type of censoring. In the case of right censoring, the ratio [latex]r / n[/latex] is the fraction of items which are observed to fail. When [latex]r / n[/latex] is close to one, the data set is referred to as a lightly censored data set; when [latex]r / n[/latex] is close to zero, the data set is referred to as a heavily censored data set. In the reliability setting, many data sets are heavily censored because the items have long lifetimes. In the biomedical setting, certain cancers have long remission times, resulting in heavily censored data sets.
Of the following three approaches to handling the problem of censoring, only one is both valid and practical. The first approach is to ignore all the censored values and to perform analysis only on those items that were observed to fail. Although this simplifies the mathematics involved, it is not a valid approach. If, for example, this approach is used on a right-censored data set, the analyst is discarding the right-censored values, and these are typically the items that have survived the longest. In this case, the analyst arrives at an overly pessimistic result concerning the lifetime distribution because the best items (that is, the right-censored observations) have been excluded from the analysis. A second approach is to wait for all the right-censored observations to fail. Although this approach is valid statistically, it is not practical. In an industrial setting, waiting for the last light bulb to burn out or the last machine to fail may take so long that the product being tested will not get to market in time. In a medical setting, waiting for the last patient to die from a particular disease may take decades. For these reasons, the proper approach is to handle censored observations probabilistically, including the censored values in the likelihood function.
The likelihood function for a censored data set can be written in several different equivalent forms. Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be mutually independent observations denoting lifetimes sampled randomly from a population. The corresponding right-censoring times are denoted by [latex]c_1, \, c_2, \, \ldots, \, c_n[/latex]. The ti and ci values are assumed to be independent, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. In the case of Type I right censoring, [latex]c_1 = c_2 = \cdots = c_n = c[/latex]. The set U contains the indexes of the items that are observed to fail during the test (that is, the uncensored observations):
The set C contains the indexes of the items whose failure time exceeds the corresponding censoring time (that is, those that are right censored):
This notation, along with an important notion known as alignment, are illustrated in the next example.
The usual form for right-censored lifetime data is given by the pairs [latex](x_i, \, \delta_i)[/latex], where [latex]x_i = \min \{t_i, \, c_i\}[/latex] and δi is a censoring indicator variable:
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The [latex](x_i, \, \delta_i)[/latex] pairs can be reconstructed from the [latex](t_i, \, c_i)[/latex] pairs and vice versa. Hence, δi is 1 if the failure of item i is observed and 0 if the failure of item i is right censored, and xi is the failure time (when [latex]\delta_i = 1[/latex]) or the censoring time (when [latex]\delta_i = 0[/latex]). For the vector of unknown parameters [latex]\boldsymbol{\theta} = (\theta_1, \, \theta_2, \, \ldots, \, \theta_p) ^ \prime[/latex], ignoring a constant factor, the likelihood function is
where [latex]S (c_i, \, \boldsymbol{\theta})[/latex] is the survivor function of the population distribution with parameters [latex]\boldsymbol{\theta}[/latex] evaluated at censoring time ci, [latex]i \, \in \, C[/latex]. The reason that the survivor function is the appropriate term in the likelihood function for a right-censored observation is that [latex]S(c_i, \, \boldsymbol{\theta})[/latex] is the probability that item i survives to ci. The log likelihood function is
or
Since the probability density function is the product of the hazard function and the survivor function, the log likelihood function can be simplified to
or
where the second summation now includes all n items on test. Finally, to write the log likelihood in terms of the hazard and cumulative hazard functions only,
since [latex]H(t) = -\ln \, S(t)[/latex]. The choice of which of these three expressions for the log likelihood to use for a particular distribution depends on the particular forms of [latex]S(t)[/latex], [latex]f(t)[/latex], [latex]h(t)[/latex], and [latex]H(t)[/latex]. In other words, one of the distribution representations may possess a mathematical form that is advantageous over the others.
The next example will use the last version of the log likelihood function to find a maximum likelihood estimator and an asymptotically exact confidence interval for an unknown parameter.
To summarize the material introduced so far in this chapter, point estimators are statistics calculated from a data set to estimate an unknown parameter. Confidence intervals reflect the precision of a point estimator. The most common technique for determining a point estimator for an unknown parameter is maximum likelihood estimation, which involves finding the parameter value(s) that make the observed data values the most likely. The maximum likelihood estimators are usually found by using calculus to maximize the log likelihood function. Most population lifetime distributions do not have exact confidence intervals for unknown parameters, so the asymptotic properties of the likelihood function can be used to generate approximate confidence intervals for unknown parameters. Finally, many data sets in reliability are censored, which means that only a bound is known on the lifetime for one or more of the data values. The most common censoring mechanism is known as right censoring, where only a lower bound on the lifetime is known. The number of items on test is denoted by n and the number of observed failures is denoted by r.
The next section applies the techniques developed so far in this chapter to the exponential distribution.
5.4 Exponential Distribution
The exponential distribution is popular due to its tractability for parameter estimation and inference. The exponential distribution can be parameterized by either its population rate λ or its population mean [latex]\mu = 1 / \lambda[/latex]. Using the rate to parameterize the distribution, the survivor, density, hazard, and cumulative hazard functions are
for [latex]t \ge 0[/latex]. Note that the unknown parameter λ has been added as an argument in these lifetime distribution representations because it is now also an argument in the likelihood function and is estimated from data.
All the analysis in this and subsequent sections assumes that a random sample of n items from a population has been placed on a test and subjected to typical environmental conditions. Equivalently, [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] are independent and identically distributed random lifetimes from a particular population distribution (exponential in this section). As with all statistical inference, care must be taken to ensure that a random sample of lifetimes is collected. Consequently, random numbers should be used to determine which n items to place on test. In a reliability setting, laboratory conditions should adequately mimic field conditions. Only representative items should be placed on test because items manufactured using a previous design may have a different failure pattern than those with the current design. This is more difficult in a biomedical setting because of inherent differences between patients.
Four classes of data sets (complete, Type II right censored, Type I right censored, and randomly right censored) are considered in separate subsections. In all cases, n is the number of items placed on test and r is the number of observed failures.
5.4.1 Complete Data Sets
A complete data set is typically the easiest to analyze because extensive analytical work exists for finding point and interval estimators for parameters. Also, by testing each item to failure, we have equal confidence in the fitted model in both the left-hand and right-hand tails of the distribution. A heavily right-censored data set, on the other hand, might fit well in the left-hand tail of the distribution where failures were observed, but we have less confidence in the right-hand tail of the distribution where there were few or no failures.
A complete data set consists of failure times [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex]. Although lowercase letters are used to denote the failure times here to be consistent with the notation for censoring times, the failure times are nonnegative random variables. The likelihood function can be written as a product of the probability density functions evaluated at the failure times:
Note that the [latex]{\boldsymbol t}[/latex] argument has been left out of the likelihood expression for compactness. Using the last expression for the log likelihood function (adapted for a complete data set) from Section 5.3,
For the exponential distribution, this is
To determine the maximum likelihood estimator for λ, the single-element score vector
also known as the score statistic, is equated to zero and solved for λ, yielding
where the denominator is often referred to as the total time on test. Not surprisingly, the maximum likelihood estimator [latex]\hat \lambda[/latex] is the reciprocal of the sample mean.
Information matrices. To find the information matrix associated with a complete data set from an exponential(λ) population, the derivative of the score statistic is required:
Taking the expected value of the negative of this quantity yields the [latex]1 \times 1[/latex] Fisher information matrix
If the maximum likelihood estimator [latex]\hat{\lambda}[/latex] is used as an argument in the negative of the second partial derivative of the log likelihood function, the [latex]1 \times 1[/latex] observed information matrix is obtained:
Confidence interval for λ. Asymptotic confidence intervals for λ based on the likelihood ratio statistic or the observed information matrix are unnecessary for a complete data set because the sampling distribution of [latex]\sum_{\,i\,=\,1}^{n} t_i[/latex] is tractable. In particular, from Theorem 4.5,
has the chi-square distribution with 2n degrees of freedom. Therefore, with probability [latex]1-\alpha[/latex],
where [latex]\chi_{2n, \, p}^2[/latex] is the ([latex]1 - p[/latex])th fractile of the chi-square distribution with 2n degrees of freedom. Performing the algebra required to isolate λ in the middle of the inequality yields an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for λ.
A well-known example of a randomly right-censored data set is drawn from the biostatistical literature. The focus here is on determining an estimate of the remission rate of a complete data set of remission times for patients in a control group.
The importance of assessing model adequacy applies to all fitted distributions—not just the exponential distribution. Furthermore, if a modeler knows the failure physics (for example, fatigue crack growth) underlying a process, then an appropriate probability model that is consistent with the failure physics should be chosen.
So far we have fitted the exponential distribution to two complete data sets: the ball bearing failure times from Example 5.5 and the 6–MP remission times for the control group from Example 5.6. We visually assessed the two fits in Figures 5.7 and 5.10 by comparing the empirical survivor function, which takes a downward step of [latex]1 / n[/latex] at each data value, with the fitted survivor function [latex]S(t) = e ^ {- \hat \lambda \kern 0.02em t}[/latex] and concluded that the exponential distribution did a very poor job of approximating the ball bearing failure times and a (barely) adequate job of approximating the remission times of the patients in the control group of the 6–MP clinical trial. This visual assessment was subjective and was followed by a formal goodness-of-fit test in order to draw these conclusions for the 6–MP remission times.
Confidence intervals for measures other than λ. It is possible to find point and interval estimators for measures other than λ by using the invariance property for maximum likelihood estimators and by rearranging the confidence interval formula. Define
as the lower and upper bounds on the exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for λ. If the measure of interest is [latex]\mu = 1 / \lambda[/latex], for example, then the point estimator is the sample mean [latex]{\hat{\mu} = \frac{1}{n} \sum_{i\,=\,1}^{n} t_i}[/latex]. Rearranging the confidence interval
by taking reciprocals yields the exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for μ:
As a second example, consider the probability of survival to a fixed time t, [latex]S(t)= e^{-\lambda t}[/latex]. By the invariance property of maximum likelihood estimators, the maximum likelihood estimator for the survivor function at time t is
A confidence interval for [latex]S(t)[/latex], on the other hand, can be found by rearranging the confidence interval
in the following fashion:
These formulas for point and interval estimates for quantities other than λ are illustrated next for a complete data set that is assumed to be drawn from an exponential population.
Although the manipulation of the confidence interval for λ is performed here in the case of a complete data set, these techniques may also be applied to any of the right-censoring mechanisms to be described in the next three subsections.
5.4.2 Type II Censored Data Sets
A life test of n items that is terminated when r failures have occurred produces a Type II right-censored data set. The previous subsection is a special case of Type II censoring when [latex]r = n[/latex]. As before, assume that the failure times are [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex], the test is terminated upon the rth ordered failure, the censoring times are [latex]c_1 = c_2 = \cdots = c_n = t_{(r)}[/latex] for all items, and [latex]x_i = \min \{t_i, \, c_i \}[/latex] for [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
Since [latex]h(t, \, \lambda ) = \lambda[/latex] and [latex]H(t, \, \lambda ) = \lambda t[/latex] for [latex]t \ge 0[/latex], the log likelihood function is
because there are r observed failures. The expression
where [latex]t_{(1)} < t_{(2)} < \cdots < t_{(r)}[/latex] are the order statistics of the observed failure times, is the total time on test. It represents the total accumulated time that the n items accrue while on test.
To determine the maximum likelihood estimator, the log likelihood function is differentiated with respect to λ,
and is equated to zero, yielding the maximum likelihood estimator.
So the maximum likelihood estimator of the failure rate is the ratio of the number of observed failures to the total time on test. The second partial derivative of the log likelihood function is
so the information matrix is
and the observed information matrix is
Exact confidence intervals and hypothesis tests concerning λ can be derived by using the result
where [latex]\chi^2 (2r)[/latex] is the chi-square distribution with 2r degrees of freedom. This result can be proved in a similar fashion to Theorem 4.5 of the exponential distribution from Section 4.2. Using this fact, an exact two-sided confidence interval for λ can be constructed in a similar fashion to that for a complete data set. It can be stated with probability [latex]1 - \alpha[/latex] that
Rearranging terms yields an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for the failure rate λ.
Hypothesis testing, which is the rough equivalent of interval estimation, is also possible in the case of Type II censoring because the sampling distribution of [latex]2 \lambda \sum_{\,i\,=\,1}^{n} x_i[/latex] is tractable. Some aspects of hypothesis testing in the setting of Type II censoring, such as the alternative hypothesis, one- and two-tailed tests, and p-values are illustrated in the next example. The example shows how a life test can be used to check a manufacturer's claimed mean time to failure.
The fact that the distribution of [latex]2 \lambda \sum_{\,i\,=\,1}^{n} x_i = {2r \lambda} / {\hat{\lambda}}[/latex] is independent of n implies that [latex]\hat{\lambda}[/latex] has the same precision in a test of r items tested until all have failed as that for a test of n items tested until r items have failed. So the justification for obtaining a Type II censored data set over a complete data set is time savings. The additional costs associated with this time savings are the additional [latex]n-r[/latex] test stands and the additional [latex]n-r[/latex] items to place on test.
If a limited number of test stands are available for testing, the only way to speed up the test is to perform a test with replacement in which failed items are immediately replaced with new items. This will decrease the expected time to complete the test, which is terminated when r of the items fail. The sequence of failures in this case is a Poisson process with rate [latex]n \lambda[/latex].
Although the inference for Type II censoring is tractable, the unfortunate consequence is that the time to complete the test is a random variable. Constraints on the time to run a life test may make a Type I censored data set more practical.
5.4.3 Type I Censored Data Sets
The analysis for Type I censored data sets is similar to that for the Type II censoring case. The test is terminated at time c. The censoring times for each item on test are the same: [latex]c_1 = c_2 = \cdots= c_n= c[/latex]. The number of observed failures, r, is a random variable. The total time on test in this case is
As before, the log likelihood function is
and the score statistic is
The maximum likelihood estimator for [latex]r > 0[/latex] is
the information matrix is
and the observed information matrix is
The functional form of the maximum likelihood estimator is identical to the Type II censoring case. For identical values of r, Type I censoring has a larger total time on test [latex]\sum_{\,i\,=\,1}^{n} x_i[/latex] than the corresponding Type II censoring case because a Type I test ends between failures r and [latex]r + 1[/latex]. Thus the expected value of [latex]\hat{\lambda}[/latex] is smaller for Type I censoring than for Type II censoring. One problem that arises with Type I censoring is that the sampling distribution of [latex]\sum_{\,i\,=\,1}^{n} x_i[/latex] is no longer tractable, so an exact confidence interval for λ has not been established. Although many more complicated methods exist, one of the best approximation methods is to assume that [latex]2 \lambda \sum_{\,i\,=\,1}^{n} x_i[/latex] has the chi-square distribution with [latex]2r+1[/latex] degrees of freedom. This approximation, illustrated in Figure 5.13, is based on the fact that if [latex]c = t_{(r)}[/latex], then [latex]2 \lambda \sum_{\,i\,=\,1}^{n} x_i \sim \chi^2 (2r)[/latex], and if [latex]c = t_{{(r}+1)}[/latex], then [latex]2 \lambda \sum_{{\,i\,=\,1}}^{n} x_i \sim \chi^2 (2r+2)[/latex]. Since c is between [latex]t_{(r)}[/latex] and [latex]t_{(r + 1)}[/latex], [latex]2 \lambda \sum_{{\,i\,=\,1}}^{n} x_i[/latex] will be approximately chi-square with [latex]2r+1[/latex] degrees of freedom. This constitutes a proof, after a little algebra, of the following result.

5.4.4 Randomly Censored Data Sets
Many of the examples that have the random censoring mechanism for which the failure times [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] and the censoring times [latex]c_1, \, c_2, \, \ldots, \, c_n[/latex] are independent random variables are from biostatistics. Random censoring occurs frequently in biostatistics because it is not always possible to control the time patients enter and exit the study. The log likelihood function, score statistic, information matrix, and observed information matrix are the same as in the Type I censoring case. The total time on test is now simply
The sampling distribution of [latex]\sum_{\,i\,=\,1}^{n} x_i[/latex] is more complicated in this case, so asymptotic properties must be relied on to determine approximate confidence intervals for λ. In the example that follows, three different approximation procedures for determining a confidence interval for λ are illustrated.
The first technique is based on an approximation to a result that holds exactly in the Type II censoring case: [latex]2 \lambda \sum_{\,i\,=\,1}^{n} x_i \sim \chi^2 (2r)[/latex]. The second technique is based on the likelihood ratio statistic, where [latex]-2 [\ln \, L(\lambda) - \ln \, L( \hat \lambda )][/latex] is asymptotically chi-square with 1 degree of freedom. The third technique is based on the fact that the maximum likelihood estimator [latex]\hat{\lambda}[/latex] is asymptotically normal with population mean λ and a population variance that is the inverse of the observed information matrix. Since this third technique results in a symmetric confidence interval, it should only be used with large sample sizes.
|
Basis for confidence interval |
Confidence interval for λ |
Confidence interval for μ |
|---|---|---|
|
Type II censoring approximate result |
[latex]0.0115 < \lambda < 0.0439[/latex] |
[latex]22.8 < \mu < 87.2[/latex] |
|
Likelihood ratio statistic |
[latex]0.0120 < \lambda < 0.0452[/latex] |
[latex]22.1 < \mu < 83.0[/latex] |
|
Asymptotic normality of the MLE |
[latex]0.0087 < \lambda < 0.0414[/latex] |
[latex]24.1 < \mu < 115.1[/latex] |
To summarize, the maximum likelihood estimator for the failure rate λ in the random censoring case is the same as in the complete, Type II and Type I censoring cases:
Three approximate confidence intervals for λ are based on (a) an exact result from Type II censoring, (b) the asymptotic distribution of the likelihood ratio statistic, and (c) the asymptotic normality of the maximum likelihood estimator. The confidence interval based on the asymptotic normality of the maximum likelihood estimator is symmetric and is therefore recommended only in the case of a large number of items on test.
5.5 Weibull Distribution
The Weibull distribution is typically more appropriate for modeling the lifetimes of items with a strictly increasing or decreasing hazard function, such as mechanical items. Rather than looking at each censoring mechanism (for example, no censoring, Type II censoring, Type I censoring) individually, we proceed directly to the general case of random censoring.
Maximum likelihood estimators. As before, let [latex]t_1 , \, t_2 , \, \ldots , \, t_n[/latex]be the failure times, [latex]c_1 , \, c_2 , \, \ldots , \, c_n[/latex] be the associated censoring times, and [latex]{x_i = \min \{t_i, \, c_i \}}[/latex] for [latex]i= 1, \, 2, \, \ldots, \, n[/latex]. The Weibull distribution has hazard and cumulative hazard functions
and
When there are r observed failures, the log likelihood function is
and the [latex]2 \times 1[/latex] score vector has elements
and
When these equations are set equal to zero, the simultaneous equations have no closed-form solution for [latex]\hat{\lambda}[/latex] and [latex]\hat \kappa[/latex]:
One piece of good fortune, however, to avoid solving a [latex]2 \times 2[/latex] set of nonlinear equations, is that the first equation can be solved for λ in terms of [latex]\kappa[/latex] as
Notice that λ reduces to the maximum likelihood estimator for the exponential distribution when [latex]\kappa = 1[/latex]. Using this expression for λ in terms of [latex]\kappa[/latex] in the second element of the score vector yields a single, albeit more complicated, expression with [latex]\kappa[/latex] as the only unknown. After applying some algebra, this equation reduces to
which must be solved iteratively. One technique that can be used to solve this equation is the Newton–Raphson procedure, which uses
where [latex]\kappa_0[/latex] is an initial estimator. The iterative procedure can be repeated until the desired accuracy for [latex]\kappa[/latex] is achieved; that is, [latex]| \kappa_{j+1} - \kappa_j | < \epsilon[/latex], for some small positive real number ϵ. When the accuracy is achieved, the maximum likelihood estimator [latex]\hat{ \kappa}[/latex] is used to calculate [latex]\hat{\lambda} = \big(r / \sum_{\,i\,=\,1}^{n} x_i^{\hat{\kappa}}\big)^{1 / {\hat \kappa}}[/latex]. The derivative of [latex]g(\kappa)[/latex] reduces to
Determining an initial estimator [latex]\kappa_0[/latex] is not trivial. When there are no censored observations, Menon's initial estimator for [latex]\kappa_0[/latex] is
Least squares estimation can be used in the case of a right-censored data set. The Newton–Raphson procedure can fail to converge to the maximum likelihood estimators. A bisection algorithm or fixed point algorithm often provides more reliable convergence.
Fisher and observed information matrices. The [latex]2 \times 2[/latex] Fisher and observed information matrices are based on the following partial derivatives:
The expected values of these quantities are not tractable, so the Fisher information matrix does not have closed-form elements. The observed information matrix, however, can be determined by using [latex]\hat{\lambda}[/latex] and [latex]\hat{\kappa}[/latex] as arguments in these expressions.
5.6 Proportional Hazards Model
Parameter estimation for the proportional hazards model, which was introduced in Section 4.6, is considered in this section. Since there is now a vector of covariates in addition to a failure or censoring time for each item on test, special notation must be established to accommodate the covariates. The proportional hazards model has the unique feature that the baseline distribution need not be defined in order to estimate the regression coefficients associated with the covariates.
A lifetime model that incorporates a vector of covariates [latex]{\boldsymbol z} = ( z_1, \, z_2, \, \ldots, \, z_q) ^ \prime[/latex] models the impact of the covariates on survival. The reason for including this vector may be to determine which covariates significantly affect survival, to determine the distribution of the lifetime for a particular setting of the covariates, or to fit a more complicated distribution from a small data set, as opposed to fitting separate distributions for each level of the covariates.
The proportional hazards model was defined in Section 4.6 by
for [latex]t \ge 0[/latex], where [latex]h_0 (t)[/latex] is a baseline hazard function. The covariates increase the hazard function when [latex]\psi ({\boldsymbol z}) > 1[/latex] or decrease the hazard function when [latex]\psi ({\boldsymbol z}) < 1[/latex]. The goal of this section is to develop techniques for estimating the [latex]q \times 1[/latex] vector of regression coefficients [latex]\boldsymbol \beta[/latex] from a data set consisting of n items on test and r observed failure times.
The notation used to describe a data set in a lifetime model involving covariates will borrow some notation established earlier in this chapter, but also establish some new notation. As before, n is the number of items on test and r is the number of observed failures. The failure time of the ith item on test, ti, is either observed or right censored at time ci, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. As before, let [latex]x_i = \min \{t_i, \, c_i\}[/latex] and δi be a censoring indicator variable (1 for an observed failure and 0 for a right-censored value), for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. In addition, a [latex]q \times 1[/latex] vector of covariates [latex]{\boldsymbol z}_i = (z_{i1}, \, z_{i2}, \, \ldots, \, z_{iq}) ^ \prime[/latex] is collected for each item on test, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. Thus, [latex]z_{ij}[/latex] is the value of covariate j for item i, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex] and [latex]j = 1, \, 2, \, \ldots, \, q[/latex]. This formulation of the problem can be stated in matrix form as
Each row in the [latex]{\boldsymbol Z}[/latex] matrix consists of the values of the q covariates collected on a particular item. The matrix approach is useful because complicated systems of equations can be expressed compactly and operations on data sets can be performed efficiently by a computer. For parameter estimation, the survivor, density, hazard, and cumulative hazard functions now have the extra arguments [latex]{\boldsymbol z}[/latex] and [latex]\boldsymbol \beta[/latex] associated with them:
$$
S(t, \, {\boldsymbol z} , \, \boldsymbol \theta , \, \boldsymbol \beta) \qquad \qquad
f(t, \, {\boldsymbol z} , \, \boldsymbol \theta , \, \boldsymbol \beta) \qquad \qquad
h(t, \, {\boldsymbol z} , \, \boldsymbol \theta , \, \boldsymbol \beta) \qquad \qquad
H(t, \, {\boldsymbol z} , \, \boldsymbol \theta , \, \boldsymbol \beta) ,
$$
for [latex]t \ge 0[/latex], where the vector [latex]\boldsymbol \theta = (\theta_1, \, \theta_2, \, \ldots, \, \theta_p) ^ \prime[/latex] consists of the p unknown parameters associated with the baseline distribution, which must be estimated along with the regression coefficients [latex]\boldsymbol \beta[/latex].
Parameter estimation for the proportional hazards model can be divided into two cases. The first case is when the baseline distribution is known. This case applies when previous test results have indicated that a particular functional form of the baseline distribution is appropriate. The second case is when the baseline distribution is unknown. This is almost certainly the case when looking at a data set of lifetimes and covariates for the first time without any guidance with respect to an appropriate baseline distribution.
5.6.1 Known Baseline Distribution
When the baseline distribution is known, the parameter estimation procedure follows along the same lines as in the previous sections. The hazard function and cumulative hazard function in the proportional hazards model are
and
for [latex]t \ge 0[/latex], where [latex]\boldsymbol \theta[/latex] is a [latex]p \times 1[/latex] vector of unknown parameters associated with the baseline distribution. For simplicity and mathematical tractability, only the log linear form of the link function, which is [latex]\psi ( {\boldsymbol z} ) = e^{\kern 0.07em \boldsymbol \beta ^ \prime {\boldsymbol z}}[/latex], is considered here. This assumption is not necessary for some of the derivations, so many of the results apply to a wider range of link functions. When the log linear form of the link function is assumed, the hazard function and cumulative hazard function become
and
for [latex]t \ge 0[/latex], where [latex]{\boldsymbol \theta}[/latex] is a [latex]p \times 1[/latex] vector of unknown parameters associated with the baseline distribution. The log likelihood function is
This expression can be differentiated with respect to all the unknown parameters to arrive at the score vector, which is then equated to zero and solved numerically to arrive at the maximum likelihood estimates.
Two observations with respect to this model formulation are important. First, the maximum likelihood estimates for [latex]\boldsymbol \theta[/latex] and [latex]\boldsymbol \beta[/latex] for most of the models in this section cannot be expressed in closed form (as was the case for the exponential distribution in Section 5.4), so numerical methods typically need to be used to find the values of the estimates. Second, the choice of whether to use a model of dependence or to examine each population separately is dependent on the number of unique covariate vectors [latex]\boldsymbol z[/latex] and the number of items on test, n. If, for example, n is large and there is only a single binary covariate (that is, only two unique covariate vectors, [latex]z_1 = 0[/latex] and [latex]z_1 = 1[/latex]), it is probably wiser to analyze each of the two populations separately by the techniques described earlier.
Although numerical methods are required to find [latex]\hat {\boldsymbol \theta}[/latex] and [latex]\hat {\boldsymbol \beta}[/latex] in general, there are closed-form expressions in a very narrow case that satisfies the following conditions.
- The log linear link function [latex]\psi ( {\boldsymbol z} ) = e^{\kern 0.07em {\boldsymbol \beta} ^ \prime {\boldsymbol z}}[/latex] is used to incorporate the vector of covariates [latex]{\boldsymbol z}[/latex] into the lifetime model.
- The baseline distribution is exponential(λ), which means that the baseline hazard function is [latex]h_0(t) = \lambda[/latex] and the baseline cumulative hazard function is [latex]H_0(t) = \lambda t[/latex] for [latex]t \ge 0[/latex].
Under these assumptions, the general form for the hazard function in the proportional hazards model
reduces to the special case
for [latex]t \ge 0[/latex]. It is often more convenient notationally to define an additional covariate, [latex]z_0 = 1[/latex], for all n items on test. This allows the baseline parameter [latex]\lambda = e^{{\beta}_0 z_0}[/latex] to be included in the vector of regression coefficients, rather than being considered separately. The baseline hazard function is effectively absorbed into the link function. In this case, the hazard function can be expressed as
for [latex]t \ge 0[/latex], where [latex]{\boldsymbol \beta} = (\beta_0, \, \beta_1, \, \ldots , \, \beta_q) ^ \prime[/latex] and [latex]{\boldsymbol z} = (z_0, \, z_1, \, \ldots , \, z_q) ^ \prime[/latex]. The corresponding cumulative hazard function is
for [latex]t \ge 0[/latex]. Using this parameterization, the log likelihood function is
Differentiating this expression with respect to βj yields the elements of the score vector
for [latex]j = 0, \, 1, \, \ldots, \, q[/latex]. When the elements of the score vector are equated to zero, the resulting set of [latex]q + 1[/latex] nonlinear equations in [latex]\boldsymbol \beta[/latex] must be solved numerically in the general case. There is a closed-form solution for this set of simultaneous equations when there is a single binary covariate, often referred to as the two-sample case.
To find the observed information matrix and the Fisher information matrix, a second partial derivative of the log likelihood function is required:
for [latex]j = 0, \, 1, \, \ldots, \, q[/latex] and [latex]k = 0, \, 1, \, \ldots, \, q[/latex]. The observed information matrix can be determined by using the maximum likelihood estimate [latex]\hat {\boldsymbol \beta}[/latex] as an argument in this second partial derivative. Thus, the [latex](j, \, k)[/latex] element of the observed information matrix is
for [latex]j = 0, \, 1, \, \ldots, \, q[/latex] and [latex]k = 0, \, 1, \, \ldots, \, q[/latex]. For computational purposes, this can be expressed in matrix form as
where [latex]\hat{{\boldsymbol B}}[/latex] is an [latex]n \times n[/latex] diagonal matrix whose elements are [latex]x_1 e^{{\kern 0.07em \hat {\boldsymbol \beta}} ^ \prime {\boldsymbol z}_1}, \, x_2 e^{{\kern 0.07em \hat {\boldsymbol \beta}} ^ \prime {\boldsymbol z}_2}, \, \ldots, \, x_n e^{{\kern 0.07em \hat {\boldsymbol \beta}} ^ \prime {\boldsymbol z}_n}[/latex]. The Fisher information matrix is more difficult to calculate because it involves the expected value of the second partial derivative:
$$
E \left[
-{\partial^2 \ln \, L({\boldsymbol \beta}) \over
\partial \beta_j \partial \beta_k} \right] =
\sum_{i\,=\,1}^n
z_{ij} z_{ik} e^{\kern 0.07em {\boldsymbol \beta} ^ \prime {\boldsymbol z}_i} E[x_i]
$$
for [latex]j = 0, \, 1, \, \ldots, \, q[/latex] and [latex]k = 0, \, 1, \, \ldots, \, q[/latex]. Determining the value of [latex]E[x_i][/latex] will be considered separately in the paragraphs that follow for uncensored ([latex]r = n[/latex]) and censored ([latex]r < n[/latex]) data sets.
For a complete data set, [latex]E[x_i] = E[t_i][/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], because there is no censoring. Since the population mean of the exponential distribution is the reciprocal of the failure rate and the ith item on test has failure rate [latex]e^{\kern 0.07em {\boldsymbol \beta} ^ \prime {\boldsymbol z}_i}[/latex], [latex]E[x_i] = e^{-\kern 0.07em {\boldsymbol \beta} ^ \prime {\boldsymbol z}_i}[/latex]. Returning to the Fisher information matrix, the [latex](j, \, k)[/latex] element is
for [latex]j = 0, \, 1, \, \ldots, \, q[/latex] and [latex]k = 0, \, 1, \, \ldots, \, q[/latex]. This result for the Fisher information matrix has a particularly tractable matrix representation
which is a function of the matrix of covariates only.
For a censored data set, the expression for [latex]E[x_i][/latex] is a bit more complicated. Since the failure rate for the ith item on test is [latex]e^{\kern 0.07em {\boldsymbol \beta} ^ \prime {\boldsymbol z}_i}[/latex],
for [latex]i = 1, \, 2, \, \ldots, \, n[/latex], by using integration by parts. This means that the [latex](j, \, k)[/latex] element of the Fisher information matrix is
where [latex]\gamma_i = e^{-e^{\kern 0.07em {\boldsymbol \beta} ^ {\kern 0.07em \prime} {\boldsymbol z}_i} c_i}[/latex] is the probability that the ith item on test is censored, for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The potential censoring time for the ith item on test, ci, must be known for each item in order to compute the Fisher information matrix, which is not always the case in practice. Letting [latex]{\boldsymbol \Gamma}[/latex] be a diagonal matrix with elements [latex]\gamma_1, \, \gamma_2, \, \ldots, \, \gamma_n[/latex], the Fisher information matrix can be written in matrix form as
which is independent of the failure times.
Before ending the discussion on the exponential baseline distribution, the two-sample case, where a binary covariate z1 is used to differentiate between the control ([latex]z_1 = 0[/latex]) and treatment ([latex]z_1 = 1[/latex]) cases, is considered. This case is of interest because the maximum likelihood estimates can be expressed in closed form. The notation for the two-sample case is summarized in Table 5.2. As before, [latex]z_0 = 1[/latex] is included in the vector of covariates to account for the baseline distribution. The set of two nonlinear equations for finding the estimates of [latex]{\boldsymbol \beta} = (\beta_0, \beta_1) ^ \prime[/latex] obtained by setting the score vector equal to 0 is
Let [latex]r_0 > 0[/latex] be the number of observed failures in the control group ([latex]z_1 = 0[/latex]), and let [latex]r_1 > 0[/latex] be the number of observed failures in the treatment group ([latex]z_1 = 1[/latex]). Since [latex]z_0 = 1[/latex] for all items on test, the equations reduce to
These equations can be further simplified by partitioning the summations based on the value of z1:
$$\begin{align*}
r_0 + r_1 -
\sum_{{i} \, | \, z_{i1} = \kern 0.07em 0} x_i e^{{\beta}_0} -
\sum_{{i} \, | \, z_{i1} = 1} x_i e^{{\beta}_0 + \beta_1 } & = 0, \\
r_1 - \sum_{{i} \, | \, z_{i1} = 1} x_i e^{{\beta}_0 + \beta_1} & = 0.
\end{align*}$$
Letting [latex]\lambda_0 = e^{{\beta}_0}[/latex] be the failure rate in the control group ([latex]z_1 = 0[/latex]) and letting [latex]\lambda_1 = e^{{\beta}_0 + \beta_1}[/latex] be the failure rate in the treatment group ([latex]z_1 = 1[/latex]), the equations become
$$\begin{align*}
r_0 + r_1 - \lambda_0
\sum_{{i} \, | \, z_{i1} =
\kern 0.07em 0} x_i - \lambda_1 \sum_{i \, | \, z_{i1} = 1}
x_i & = 0, \\
r_1 - \lambda_1 \sum_{i \, | \, z_{i1} = 1} x_i & = 0.
\end{align*}$$
When these equations are solved simultaneously, the maximum likelihood estimates for λ0 and λ1 are the same as those for the exponential distribution with two separate populations:
These estimators are the ratio of the number of observed failures to the total time on test within the two groups.
Parameter estimation for single binary covariate is ideal in the sense that the parameter estimates can be expressed in closed form. The next subsection considers the more common situation in which the baseline distribution is unknown.
5.6.2 Unknown Baseline Distribution
In many applications, the baseline distribution is not known. Furthermore, the modeler may not be interested in the baseline distribution, rather only in the influence of the covariates on survival. A technique has been developed for the proportional hazards model that allows the coefficient vector [latex]{\boldsymbol \beta}[/latex] to be estimated without knowledge of the parametric form of the baseline distribution. This type of analysis might be appropriate when the modeler wants to detect which covariates are significant, to determine which covariate is the most significant, or to analyze interactions among covariates. This technique is characteristic of nonparametric methods because it is impossible to misspecify the baseline distribution.
The focus of this estimation technique is on the indexes of the components on test, as will be seen in the derivation to follow. Since this procedure is very different from all previous point estimation derivations, an example will be carried through the derivation to illustrate the notation and the method. The purpose in this small example is to determine whether light bulb wattage influences light bulb survival. This introduction to parameter estimation will alternate between the small example and the general case. In this example and the derivation, it is initially assumed that there is no censoring and there are no tied observations.
The notation defined in the example is easily extended from three items on test with a single binary covariate to the general case. Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be n distinct lifetimes. Each lifetime ti has an associated [latex]q \times 1[/latex] vector of covariates [latex]{\boldsymbol z}_i[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The ith order statistic is given by [latex]t_{(i)}[/latex], and the risk set [latex]R(t_{(i)})[/latex] is the set of indexes of all items that are at risk just prior to [latex]t_{(i)}[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The ith element of the rank vector [latex]{\boldsymbol r} = (r_1, \, r_2, \, \ldots , r_n ) ^ \prime[/latex] is the index of the item that fails at time [latex]t_{(i)}[/latex], for [latex]i = 1, \, 2, \, \ldots , \, n[/latex]. The observed failure times and their associated indexes are equivalent to the observed order statistics and the associated rank vector. Now that the new notation has been defined, the emphasis transitions to determining the probability that a particular permutation of the indexes appears in the rank vector.
In the example, as well as in the general case, the conditional probability expression does not involve the failure times, making it possible to shorten [latex]P( r_j = i \,|\, t_{(1)}, \, t_{(2)}, \, \ldots, \, t_{(j)}, \, r_1, \, r_2, \, \ldots, \, r_{{j - 1}})[/latex] to just [latex]P( r_j = i \,|\, r_1, \, r_2, \, \ldots , \, r_{{j - 1}} )[/latex]. The probability that the jth element of the rank vector will be equal to i, given [latex]t_{(j)}[/latex] and the failure history up to [latex]t_{(j)}[/latex], is
The procedure for estimating β1 can be generalized from the example without any significant difficulties. The probability mass function for the indexes, or the likelihood function for [latex]\boldsymbol {\beta}[/latex], is now
The log likelihood is
The score vector has sth component
for [latex]s = 1, \, 2, \, \ldots, \, q[/latex]. The vector of maximum likelihood estimators [latex]\hat {\boldsymbol \beta}[/latex] is obtained when the elements of the score vector are equated to zero and solved via numerical methods. To determine an estimate for the variance of [latex]\hat {\boldsymbol \beta}[/latex], the score vector must be differentiated to calculate the observed information matrix. The diagonal elements of the inverse of the observed information matrix are asymptotically valid estimates of the variance of [latex]\hat {\boldsymbol \beta}[/latex].
There are two approaches to handle right censoring that do not significantly complicate the derivation presented thus far. The first approach is to assume that right censoring occurs immediately after a failure occurs when a failure time and right-censoring time coincide. This assumption is valid for a Type II censored data set, but will involve an approximation for more general right-censoring schemes. In this case the rank vector is shortened to only r elements, corresponding to the indexes of the observed failure times [latex]t_{(1)}, \, t_{(2)}, \, \ldots, \, t_{(r)}[/latex]. The likelihood function is
The log likelihood function is
The score vector has sth component
for [latex]s = 1, \, 2, \, \ldots, \, q[/latex]. Using the quotient rule, the derivative of the score vector is
for [latex]s = 1, \, 2, \, \ldots, \, q[/latex] and [latex]t = 1, \, 2, \, \ldots, \, q[/latex]. The elements of the observed information matrix are obtained by using the maximum likelihood estimates as arguments in the negative of this expression.
The second approach to right censoring is to write the likelihood function as the sum of all likelihoods for complete data sets that are consistent with the censoring pattern. Fortunately, this second approach yields the same likelihood function as the first approach, as illustrated by the following example.
Tied lifetimes are typically handled by an approximation. When there are several failures at the same time value, each is assumed to contribute the same term to the likelihood function. Consequently, all the items with tied failure times are included in the risk set at the time of the tied observation. This approximation works well when there are not many tied observations in the data set and has been implemented in many software packages that estimate the vector of regression coefficients [latex]\boldsymbol {\beta}[/latex].
The last example moves from the single binary covariate case to the case in which there are [latex]q > 1[/latex] covariates which can assume discrete and continuous values. The survival analysis application comes from sociology, and the analyst is attempting to determine which of the covariates significantly influences survival.
This chapter has contained a brief introduction to some of the statistical methods that are used in survival analysis. The key modeling features that indicate the use of survival analysis are (a) a population lifetime distribution with nonnegative support, (b) appreciable dispersion, (c) possibly right-censored data values, (d) possibly a vector of covariates which might influence the lifetime distribution. The exponential, Weibull, and Cox proportional hazards model were fitted to complete and right-censored data sets in this chapter.
5.7 Exercises
-
5.1 Consider a large batch of light bulbs whose lifetimes are known to have exponential(1) lifetimes. Gina knows that the population distribution is exponential, but she does not know the value of the population mean. She estimates the population mean lifetime of the light bulbs by averaging n observed lifetimes from bulbs chosen at random from the batch. Find the smallest value of n that assures, with probability of at least 0.95, that the sample mean is within 0.2 of the population mean
- exactly,
- approximately, using the central limit theorem.
-
5.2 Libby is a statistician for a light bulb company. She knows that the lifetimes of the 60-watt bulbs that her company manufactures are exponentially distributed with population mean 1500 hours. She conducts a life test in which 39 of their 60-watt bulbs are placed on life test until they fail and the average of the failure times is recorded. Find the probability that the sample mean exceeds 1600 hours using
- the central limit theorem,
- the exact distribution of the sample mean.
-
5.3 Let [latex]t_1, \, t_2, \, \ldots, \, t_{n}[/latex] be a random sample from an exponential[latex](\lambda)[/latex] population, where λ is a positive unknown failure rate parameter. Find an unbiasing constant cn so that [latex]c_n t_{(1)}[/latex] is an unbiased estimator of [latex]1 / \lambda[/latex], where [latex]t_{(1)} = \min \left\{ t_1, \, t_2, \, \ldots, \, t_n \right\}[/latex] is the first order statistic. Hint: the unbiasing constant cn is a function of the number of items on test n.
-
5.4 Debbie purchases a laptop computer with a random lifetime T whose probability distribution is a special case of the log logistic distribution with survivor function
where λ is a positive unknown scale parameter. From just a single observation of the lifetime of her laptop computer, find an exact two-sided 90% confidence interval for λ.
-
5.5 Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from an exponential population with mean θ, where θ is a positive unknown parameter. An exact two-sided 90% confidence interval for θ is
Carol is not concerned about large values of θ. Only small values of θ are of concern. What is an exact one-sided 95% confidence interval of the form [latex]\theta > k[/latex], for some constant k?
-
5.6 If [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] are n mutually independent observations from a log normal distribution with probability density function
for [latex]\sigma > 0[/latex] and [latex]-\infty < \mu < \infty[/latex], find the maximum likelihood estimators of μ and σ and exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence intervals for μ and σ in terms of [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex].
-
5.7 Let [latex]t_1, \, t_2, \, \ldots , \, t_7[/latex] be a random sample of the lifetimes of [latex]n = 7[/latex] items on test drawn from an exponential population with positive unknown mean θ.
- Find an exact two-sided 90% confidence interval for the median by finding a pivotal quantity based on the sample median [latex]t_{(4)}[/latex].
- Give an exact two-sided 90% confidence interval for the median for the [latex]n = 7[/latex] rat survival times in the treatment group from Efron and Tibshirani (1993, page 11):
- Conduct a Monte Carlo simulation experiment to provide convincing numerical evidence that the exact two-sided 90% confidence interval for the median is indeed an exact two-sided 90% confidence interval for an exponential population when θ is arbitrarily set to 1.
-
5.8 This chapter has emphasized confidence intervals. Another type of statistical interval is known as a prediction interval, which contains a future value of an observation with a prescribed probability. Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from an exponential population with a positive unknown mean θ. Conduct a Monte Carlo simulation experiment that provides convincing numerical evidence that the [latex]{100(1 - \alpha)}\%[/latex] prediction interval for [latex]t_{n+1}[/latex]
is an exact prediction interval for the arbitrary parameter settings [latex]n = 11[/latex], [latex]\alpha = 0.05[/latex], and [latex]\theta = 19[/latex].
-
5.9 Let [latex]T_1, \, T_2, \, T_3[/latex] be mutually independent random variables such that Ti is exponentially distributed with mean [latex]i \kern 0.02em \theta[/latex], for [latex]i = 1, \, 2, \, 3[/latex], where θ is a positive unknown parameter.
- Find the maximum likelihood estimator [latex]\hat \theta[/latex].
- Find the probability density function of the maximum likelihood estimator [latex]\hat \theta[/latex].
- Is [latex]\hat \theta[/latex] an unbiased estimator of θ?
- Find an exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for θ.
- Perform a Monte Carlo simulation experiment to evaluate the coverage of the confidence interval for [latex]\theta = 10[/latex] and [latex]\alpha = 0.1[/latex].
-
5.10 Let [latex]t_1, \, t_2, \, \ldots , \, t_n[/latex] be a random sample from a population with probability density function
where θ is a positive unknown parameter.
- Find the maximum likelihood estimator of θ.
- Use the invariance property to find the maximum likelihood estimator of the median of the distribution.
-
5.11 Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from a population with probability density function
where λ is a positive unknown parameter. This distribution is known as the standard Wald distribution which is a special case of the inverse Gaussian distribution Find the maximum likelihood estimator of λ.
-
5.12 Let [latex]T_1, \, T_2, \, \ldots , \, T_n[/latex] be mutually independent and identically distributed random variables from a population having probability density function
Find the limiting distribution of [latex]n \left( T_{(1)} - \theta \right)[/latex]. Support this limiting distribution by conducting a Monte Carlo simulation experiment.
-
5.13 Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from a population with probability density function
where θ is a positive unknown parameter. Calculate an asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for θ based on the asymptotic normality of the maximum likelihood estimator.
-
5.14 Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from a population with probability density function
where θ is a positive unknown parameter. This population distribution is a special case of the inverse Gaussian distribution. Calculate an asymptotically exact two-sided [latex]{100(1 - \alpha)}\%[/latex] confidence interval for θ based on the asymptotic normality of the maximum likelihood estimator. Hint: the expected value of T is [latex]E[T] = \theta[/latex].
-
5.15 Let [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] be a random sample from a population with probability density function
where θ is a positive unknown parameter. This is a special case of the log logistic distribution.
- Find the maximum likelihood estimator of θ. Hint: The maximum likelihood estimator cannot be expressed in closed form.
- Find the maximum likelihood estimate of θ for the [latex]n = 7[/latex] rat survival times (in days) of the treatment group from Efron and Tibshirani (1993, page 11):
- Find an asymptotically exact two-sided 95% confidence interval for θ based on the likelihood ratio statistic for the rat survival times from part (b).
-
5.16 If n items from an exponential population with failure rate λ are placed on a life test that is terminated after r failures have occurred, show that
where [latex]x_i = \min \{t_i, \, c_i \}[/latex], ti is the time to failure of the ith item, and ci is the right-censoring time for the ith item, [latex]i = 1, \, 2, \, \ldots, \, n[/latex].
-
5.17 If n items from an exponential population with failure rate λ are placed on a life test that is terminated after r failures have occurred, find the expected time to complete the test if
- failed items are not replaced,
- failed items are immediately replaced with new items.
-
5.18 Find the score, maximum likelihood estimator, and Fisher information matrix for a Type II censored random sample from a population with
where θ is a positive unknown parameter.
-
5.19 The lifetimes of studio light bulbs, measured in days, is exponentially distributed with an unknown failure rate λ. James places n studio light bulbs on test at noon on one day and subsequently checks for failed bulbs at noon on subsequent days until all bulbs have failed. Let [latex]r_1, \, r_2, \, \ldots, \, r_k[/latex] be the number of observed bulb failures, some of which may be zero, on the k days that the bulbs are inspected. Find the maximum likelihood estimator for λ. Also, give the maximum likelihood estimate for the data values [latex]r_1 = 8[/latex], [latex]r_2 = 5[/latex], [latex]r_3 = 2[/latex], [latex]r_5 = 1[/latex], and all other ri values equal zero.
-
5.20 James's friend Alexandra decides to simplify matters from the previous question by assuming that all failures that occur during any interval occur at midnight. What is Alexandra's maximum likelihood estimator for λ as a function of n and [latex]r_1, \, r_2, \, \ldots, \, r_k[/latex]?
-
5.21 Dre conducts a life test on n items from an exponential population with mean θ. He observes only the value of a single order statistic [latex]t_{(k)}[/latex], where k is known. So [latex]k - 1[/latex] lifetimes are left censored at [latex]t_{(k)}[/latex], one lifetime is observed at [latex]t_{(k)}[/latex], and [latex]n - k[/latex] lifetimes are right censored at [latex]t_{(k)}[/latex].
- What is the score statistic for estimating θ?
- What is the maximum likelihood estimator for θ when [latex]n = 30[/latex], [latex]k = 11[/latex], and [latex]t_{(11)} = 15.5[/latex]?
-
5.22 Consider a Type II right-censored life test with n items on test and [latex]r = 1[/latex] failure is observed at time [latex]t_{(1)}[/latex]. Assume that the items placed on the life test have lifetimes that are well described by a Rayleigh(λ) population.
- What is the maximum likelihood estimator for λ?
- What is an exact confidence interval for λ?
- What is the expected width of the confidence interval from part (b)?
- Verify the coverage and expected width of the exact confidence interval for [latex]\lambda = 2[/latex], [latex]n = 7[/latex], and [latex]\alpha = 0.05[/latex] via Monte Carlo simulation.
-
5.23 A randomly right-censored data set is collected from a population with hazard function
where θ is a positive parameter.
- Find the maximum likelihood estimator [latex]\hat \theta[/latex].
- Give an expression for the observed information matrix.
- Give an asymptotically exact confidence interval for θ based on the observed information matrix.
-
5.24 Candice conducts a life test in which n items are simultaneously placed on test at time 0. The test is concluded at time [latex]c > 0[/latex]. Assuming that the lifetimes of the items are from an exponential population with mean θ, find the distribution of the number of failures that occur by time c.
-
5.25 Show that when a random sample is drawn an exponential(λ) population with Type II right censoring
where [latex]\chi^2 (2r)[/latex] is the chi-square distribution with 2r degrees of freedom.
-
5.26 Consider a Type II right censored sample of n items on test and r observed failures drawn from an exponential population with mean θ. Show that the maximum likelihood estimate [latex]\hat{\theta}[/latex] is unbiased.
-
5.27 Assume that a life test without replacement is conducted on n items from an exponential population with failure rate λ. The exact failure times are not known, but the test is terminated upon the rth ordered failure at time [latex]t_{(r)}[/latex]. Find a point estimator for λ.
-
5.28 Consider a population of items with exponential(λ) lifetimes. A life test with replacement is terminated when r failures occur or at time c, whichever occurs first. This is a combination of Type I and Type II right censoring. Find the expected number of items that fail during the test as a function of λ.
-
5.29 For a life test of n items with exponential(λ) lifetimes (items are not replaced upon failure) which is continued until all items fail, show that
where λ is the population failure rate and [latex]\hat{\lambda}[/latex] is the maximum likelihood estimator for λ. Thus, an unbiasing constant for [latex]\hat{\lambda}[/latex] is [latex]u_n = {(n - 1)} / n[/latex]. Equivalently,
Find an unbiasing constant for the case of Type II right censoring.
-
5.30 Give a point and 95% interval estimator for the median lifetime of the 6–MP treatment group assuming that the data have been drawn from an exponential(λ) population.
-
5.31 Consider the following Type II right censored data set for the lifetime of a product ([latex]n = 5[/latex] and [latex]r = 3[/latex]) drawn from an exponential population with failure rate λ:
- Find the maximum likelihood estimator for the mean of the population.
- Find the maximum likelihood estimator for [latex]S(5)[/latex].
- Find an exact two-sided 80% confidence interval for [latex]E\left[T ^ 3 \right][/latex].
- Find an exact one-sided 95% lower confidence interval for [latex]S(5)[/latex].
- Find the p-value for the test [latex]H_0: \lambda = 0.04[/latex] versus [latex]H_1: \lambda > 0.04[/latex].
- Find the value of the log likelihood function at the maximum likelihood estimate.
- Find the value of the observed information matrix.
- Assume the data values
constitute a complete data set for a different product. Find an exact two-sided 90% confidence interval for the ratio of the failure rates of the two products if both are assumed to come from exponential populations.
-
5.32 Sara observes a single observed lifetime T from an exponential(λ) population, where λ is a positive unknown rate parameter. Find an exact two-sided 95% confidence interval for λ.
-
5.33 Justin places a single item is placed on test ([latex]n = 1[/latex]). The only information that is available is that the item failed between times a and b, where [latex]a < b[/latex]. In other words, the single item's lifetime is interval censored. Assuming that the population time to failure is exponential(λ), what is the maximum likelihood estimator of λ?
-
5.34 Natalie conducts a life test with [latex]n = 19[/latex] items on test and random right censoring. Let [latex]t_1, \, t_2, \, \ldots , \, t_{19}[/latex] be the independent exponential(2) times to failure. Let [latex]c_1, \, c_2, \, \ldots , \, c_{19}[/latex] be the independent exponential(1) censoring times, which are independent of the times to failure. Use Monte Carlo simulation to estimate the actual coverage of the following approximate confidence interval procedures for the population failure rate λ at for [latex]\alpha = 0.05[/latex].
- The confidence interval consisting of all λ satisfying
- The confidence interval consisting of all λ satisfying
- The confidence interval consisting of all λ satisfying
Replicate the experiment so as to estimate the actual coverages to three digits of accuracy.
-
5.35 Sixty-watt light bulb lifetimes are known to be exponentially distributed with unknown positive population mean θ from previous test results. The company that produces these light bulbs would like to estimate θ by testing n bulbs to failure at one facility and m bulbs to failure at a second facility. Let [latex]X_1, \, X_2, \, \ldots , \, X_n[/latex] be the independent lifetimes of the bulbs tested at the first facility; let [latex]Y_1, \, Y_2, \, \ldots , \, Y_m[/latex] be the independent lifetimes of the bulbs tested at the second facility. An unbiased estimate of θ is the convex combination
where [latex]0 < p < 1[/latex], [latex]\hat \theta_X = \bar X[/latex] is the maximum likelihood estimator of θ for the data from the first facility, and [latex]\hat \theta_Y = \bar Y[/latex] is the maximum likelihood estimator of θ for the data from the second facility. Find the value of p that minimizes [latex]V\big[ \kern 0.01em \hat \theta \kern 0.04em \big][/latex].
-
5.36 Ash would like to test the hypothesis
versus
using a single value T from an exponential(λ) population, where λ is a positive unknown population failure rate. The null hypothesis is rejected if [latex]T < 0.01[/latex]. Find the significance level α for the test.
-
5.37 Let T be an observation from an exponential population with positive unknown population mean θ. This observation is used to test
versus
- Find the critical value for the test for a fixed significance level α.
- Find β for a fixed significance level α.
-
5.38 Paul collects a random sample [latex]t_1, \, t_2, \, \ldots , \, t_n[/latex] from an exponential population with positive unknown mean θ. Show that the sample mean, [latex]\bar{t}[/latex], and n times the first order statistic, [latex]n t_{(1)}[/latex], are both unbiased estimators of θ.
-
5.39 Jessica and Mary collect a random sample [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] of light bulb lifetimes drawn from an exponential(λ) population, where λ is a positive unknown failure rate. The bulbs are stamped with “1000 hour MTTF,” indicating that the mean time to failure equals 1000 hours. They would like to determine whether there is statistical evidence in the sample that indicates the bulbs last longer than 1000 hours.
- State the appropriate H0 and H1.
- Jessica uses the test statistic [latex]\bar{t}[/latex] and Mary uses the test statistic [latex]nt_{(1)}[/latex] to test the hypothesis. Find the critical values for their test statistics when [latex]\alpha = 0.05[/latex] and [latex]n = 10[/latex].
- Draw the power curves associated with each of the test statistics from part (b) on the same set of axes using a computer. Again assume that [latex]\alpha = 0.05[/latex] and [latex]n = 10[/latex].
-
5.40 Camille observes a single lifetime T from an exponential population with a positive unknown population mean θ. She would like to test
versus
at [latex]\alpha = 0.07[/latex] using T as a test statistic.
- Find the critical value c for this test.
- Plot the power function for this test.
-
5.41 Ellen collects a random sample [latex]t_1, \, t_2, \, \ldots, \, t_{10}[/latex] of light bulb lifetimes from an exponential(λ) population, where λ is a positive unknown failure rate. Ellen is a reliability engineer. She is confident from previous test results that the time to failure for these light bulbs is exponentially distributed. She is interested in testing whether a manufacturer's claim that the population mean time to failure for the bulbs is 1000 hours. So she would like to test
versus
She is in a hurry. She places ten bulbs on test and only observes the first bulb fail at [latex]t_{(1)} = 14[/latex] hours, and would like to draw a conclusion at 14 hours. Give the p-value for the test based on the value of this single order statistic.
-
5.42 Liz collects a random sample of lifetimes [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] from an exponential(λ) distribution, where λ is a positive unknown failure rate parameter. She conducts a significance test of
versus
which achieves a p-value of [latex]p = 0.07[/latex] for a particular data set. If she then computes an exact two-sided 95% confidence interval for λ for this particular data set, will the confidence interval contain 1?
-
5.43 Karen fits the ball bearing data set to the Weibull distribution parameterized as
yielding maximum likelihood estimates [latex]\hat{\lambda} = 0.0122[/latex] and [latex]\hat{\kappa} = 2.10[/latex]. Ute also wants to fit the same data set to the Weibull distribution, but she uses the parameterization
What will be the maximum likelihood estimates [latex]\hat{\rho}[/latex] and [latex]\hat{\beta}[/latex] that Ute obtains for the ball bearing data set?
-
5.44 Jay conducts a life test with [latex]n = 5[/latex] items on test which is terminated when [latex]r = 3[/latex] items have failed. Failed items are not replaced in this traditional Type II right-censored data set. Assuming that the time to failure of an item in the population has a Weibull([latex]\lambda, \, \kappa[/latex]) distribution with known, positive parameters λ and [latex]\kappa[/latex], what is the probability density function of the time to complete the life test?
-
5.45 Jennie collects a random sample [latex]t_1, \, t_2, \, \ldots, \, t_7[/latex] from a Rayleigh population with probability density function
where θ is a positive unknown parameter. She would like to test
versus
using the test statistic [latex]t_{(1)} = \min \left\{ t_1, \, t_2, \, \ldots, \, t_7 \right\}[/latex], which assumes the value [latex]t_{(1)} = 6[/latex]. Find the p-value for her test.
-
5.46 Mildred collects a random sample [latex]t_1, \, t_2, \, \ldots, \, t_n[/latex] from a Rayleigh[latex](\lambda)[/latex] population with survivor function
where λ is a positive unknown parameter.
- Find the maximum likelihood estimator of λ.
- Show that the log likelihood function is maximized at the maximum likelihood estimator [latex]\hat{\lambda}[/latex].
- Given that the expected value of T is [latex]E[T] = {\sqrt{\pi}} / (2 \lambda)[/latex], find the method of moments estimator of λ.
-
5.47 Find the elements of the score vector for the log logistic distribution for a randomly right-censored data set.
-
5.48 Bryan places n items on test and observes r failures. Assuming that the failure times of the items follow the log logistic distribution and censoring is random, set up an expression for the boundary of a 95% confidence region for the shape parameter [latex]\kappa[/latex] and scale parameter λ of the log logistic distribution based on the likelihood ratio statistic. Assume that the survivor function for the log logistic distribution is
for [latex]\lambda > 0[/latex] and [latex]\kappa > 0[/latex]. It is not necessary to solve for the maximum likelihood estimators.
-
5.49 Consider a proportional hazards model with [latex]n = 3[/latex] items on test and distinct failure times [latex]t_1, \, t_2, \, t_3[/latex]. Compute the joint probability mass function values for the [latex]3! = 6[/latex] possible rank vectors, and show that they sum to 1.
-
5.50 Give the equations that must be solved in order to find the maximum likelihood estimators [latex]\hat{\lambda}[/latex], [latex]\hat{\kappa}[/latex], and [latex]\hat {\boldsymbol beta}[/latex] for a proportional hazards model with log logistic baseline distribution and log linear link function. A random right-censoring scheme is used.
-
5.51 Joyce fits the Cox proportional hazards model with unknown baseline distribution given in Examples 5.14, 5.15, and 5.16 to the [latex]n = 3[/latex] light bulb failure times. The purpose of the study was to determine the effect of wattage on survival for 60-watt and 100-watt light bulbs.
- What is the value of the regression coefficient for wattage if it were coded as [latex]z = 60[/latex] and [latex]z = 100[/latex] rather than as a binary covariate?
- Write a short paragraph indicating whether or not these two approaches are fundamentally equivalent ways of coding the covariate. If they differ, is one method of coding the covariate superior to the other for the purpose of the study?
-
5.52 Survival times (in weeks) for two groups of leukemia patients (AG positive and AG negative blood types), along with an additional covariate, white blood cell count are given in Feigl, P. and Zelen, M., “Estimation of Exponential Survival Probabilities with Concomitant Information,” Biometrics, Vol. 21, No. 4, pp. 826–838, 1965, and are displayed below.
AG positive group
AG negative group
Survival time
White blood count
Survival time
White blood count
65
2300
56
4400
156
750
65
3000
100
4300
17
4000
134
2600
7
1500
16
6000
16
9000
108
10500
22
5300
121
10000
3
10000
4
17000
4
19000
39
5400
2
27000
143
7000
3
28000
56
9400
8
31000
26
32000
4
26000
22
35000
3
21000
1
100000
30
79000
1
100000
4
100000
5
52000
43
100000
65
100000
- Fit the Cox proportional hazards model to the survival times. Code the blood type as the indicator variable z1, using 1 for AG positive and 0 for AG negative. The second covariate z2 is the natural logarithm of the white blood cell counts minus the sample mean of the natural logarithms of the white blood cell counts. Include the interaction term [latex](z_1 - \bar z_1) z_2[/latex] in the model. Use the Breslow method for handling tied survival times.
- Write a sentence interpreting the sign of [latex]\hat \beta_1[/latex], [latex]\hat \beta_2[/latex], and [latex]\hat \beta_3[/latex] in terms of risk to the patient.
- Give a 95% confidence interval for β1.
- If covariates associated with p-values that are less than 0.10 are considered statistically significant, what is the fitted hazard function for a leukemia patient with baseline hazard function [latex]h_0(t)[/latex], white blood cell count 9000 who has AG positive blood type? Hint: The sample mean of the natural logarithms of the white blood cell types is 9.52 and the mean of the blood types coded as an indicator variable is [latex]17 / 33 = 0.515[/latex].
-
5.53 Consider the Cox proportional hazards model with a single ([latex]q = 1[/latex]) binary covariate z1, an exponential(λ) baseline distribution, and a log linear link function. The baseline distribution can be absorbed into the link function by creating an artificial covariate [latex]z_0 = 1[/latex] and setting [latex]\lambda = e ^ {\beta_0 z_0}[/latex].
- For a randomly right-censored data set, find the score vector.
- For a randomly right-censored data set, find closed-form expressions for the maximum likelihood estimators [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex].
- For the [latex]n = 3[/latex] observations given in vector form below, calculate the maximum likelihood estimates [latex]\hat \beta_0[/latex] and [latex]\hat \beta_1[/latex].
- What is the hazard function of the fitted model for the data from part (c)?
- Use the observed information matrix to give approximate two-sided 95% confidence intervals for β0 and β1 for the data from part (c).
- Give the p-values for testing the hypotheses
for [latex]i = 0, \, 1[/latex], for the data from part (c).
-
5.54 The wattage of the [latex]n = 3[/latex] light bulbs in Example 5.16 was coded as the covariate [latex]z_1 = 0[/latex] for a 60-watt bulb and [latex]z_1 = 1[/latex] for a 100-watt bulb. When the Cox proportional hazards model with an unspecified baseline hazard function was fit to the data set, the point estimate for the regression parameter was [latex]\hat \beta_1 = -0.347[/latex]. Without doing the derivation from scratch, what is the point estimate for the regression parameter if the wattage (that is, 60 watts or 100 watts) of the bulb were used as the covariate.
-
5.55 Mark fits a Cox proportional hazards model with unknown baseline distribution to a data set of drill bit failure times (measured in number of items drilled) with [latex]q = 2[/latex], for which the covariates denote the turning speed (revolutions per minute, rpm) and the hardness of the material (Brinell hardness number, BHN) being drilled. The turning speeds range from 2400 to 4800 rpm and the hardness of the materials ranges from 250 to 440 BHN. Interactions are not considered and the variables are not centered. The fitted model has estimated regression vector [latex]\hat {\boldsymbol \beta} = (0.014, \, 0.45) ^ \prime[/latex], and the inverse of the observed information matrix is
Write a paragraph interpreting these results.

