Chapter 7 Time Series Basics
This chapter defines a time series, describes where a time series falls with respect to other stochastic processes, introduces some basic properties of time series, and introduces some basic operations that can be applied to a time series. The presentation given here does not replace a full-semester class on time series analysis, but does provide an elementary introduction to the topic. Each section ends with a brief review of the computational tools available in R for time series analysis.
7.1 The Big Picture
A time series is a sequence of observed data values that are collected over time. The analysis of a time series is an important sub-discipline of statistics and data science that has applications in a variety of areas, including economics, business, science, and engineering.
Classical statistical methods rely on the assumption that the data values collected constitute a simple random sample, which implies that data values are realizations of mutually independent and identically distributed random variables. This is nearly universally not the case in time series analysis because nearby observations collected over time tend to be correlated. Special probability models and associated statistical methods have been developed to account for this correlation. When the focus is on the correlation between observations in the time series, analysis tools from the time domain are employed. When the focus is on the periodic behavior in the time series, analysis tools from the frequency domain are employed. We begin our exploration of time series with a subsection containing examples.
7.1.1 What is a Time Series?
The essence of a time series is best captured in a sequence of examples. The first example is the monthly number of kilowatt hours required for powering the utilities in my home from 2011 through 2018. The second example is the monthly number of international airline passengers between 1949 and 1960. The third example is a realization of what is known as Gaussian white noise. The fourth example is a realization of what is known as a random walk.
The home energy consumption example has shown that significant insight concerning a time series can be gleaned by an understanding of the context associated with the time series and the crucial step of making a simple plot of the data values over time. We will return to the home energy consumption time series later for further analysis. The next time series illustrates the increase in international airline travel between 1949 and 1960.
Before describing a third example of a time series, we define some notation. A common convention in probability theory is to use uppercase letters, such as X and Y, to denote random variables. When encountering a time series, it is often helpful to subscript the random variable denoting the time series observations with t, for time, as Xt. So a time series consisting of the time-ordered observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] can be referred to in the abstract as [latex]\left\{ X_t \right\}[/latex], which is more compact. But when referring to a specific realization of a time series (either collected as data or generated by a computer via simulation) consisting of the time-ordered observations [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], we switch to the lowercase version [latex]\left\{ x_t \right\}[/latex]. This is why the vertical axes in Figures 7.1 and 7.2 were labeled xt for the [latex]n = 96[/latex] home energy consumption observations from Example 7.1 and the [latex]n = 144[/latex] airline passenger counts from Example 7.2. The notation developed in this paragraph will be apparent in the formal definition of noise, which is defined next.
Instead of analyzing a realization of a time series as in the previous two examples, time series analysts often formulate and fit a probability model for a time series. This process is roughly the time series equivalent of fitting a univariate probability distribution, such as the normal distribution, to a data set. We will again refer to the time series as [latex]\left\{ X_t \right\}[/latex] when constructing such a time series model, but when the index values for t are not obvious by context, we add the additional parameter T, which is the set of allowable values for t using [latex]\left\{ X_t, \, t \in T \right\}[/latex]. The set T will almost universally be either the set of all integers (when it is necessary to consider observations with negative t values) or the set of all nonnegative integers (when a time origin is necessary).
Most time series cannot be described by a deterministic function. In order to inject randomness into the time series model, it has become common practice to define noise, which consists of random shocks that will make a time series model stochastic rather than deterministic. Three varieties of noise used by time series analysts are defined next. In some application areas, noise might be referred to as error or disturbance.
It is clear from Definition 7.1 that the three varieties of noise were defined from the more general case to the more specific case so that
All three varieties share common population means and variances:
These three probability models are, in some sense, the simplest possible time series models, although time series that are well-modeled by the three models are very rare in practice. Rather than approximating a real-world time series, they serve as building blocks for more realistic models. They are often used to describe the probability distribution of error terms in a probability model for a time series. In the next example, you will see a plot of a realization of Gaussian white noise.
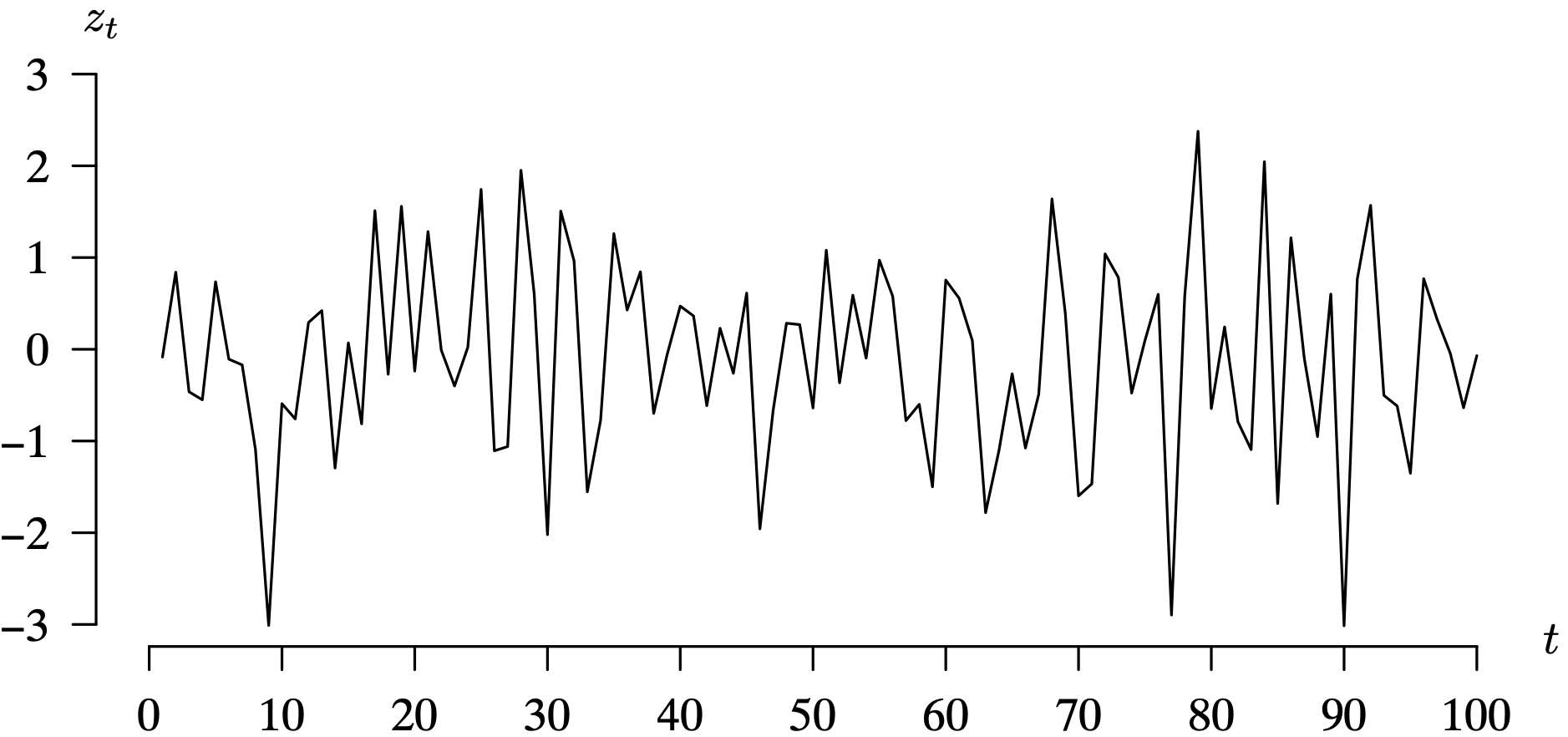
Long Description for Figure 7.3
The horizontal axis t ranges from 0 to 100 in increments of 10 units. The vertical axis measures z subscript t and ranges from negative 3 to 3 in increments of 1 unit. The noise value at time t equals 0 is 0, fluctuates, and reaches a minimum of negative 3.015 at t equals 10. It then increases and vacillates between negative 2 and 2 from t equals 15 to t equals 75, reaching a maximum value of 2.3 at t equals 79, and achieving a minimum value of negative 3.01 at t equals 90. All data are estimated.
Most time series that are encountered in practice do not behave in a fashion that approximates white noise, iid noise, or Gaussian white noise. It is more often the case that the value of the observation in the time series at time t will depend on the values of one or more of the previous observations in the time series. One time series model that exhibits this dependency is known as a random walk, which is defined and illustrated next.
In this section, we have encountered four examples of time series:
- a time series of [latex]n = 96[/latex] monthly home energy consumption observations,
- a time series of [latex]n = 144[/latex] monthly international airline passenger counts,
- a time series of [latex]n = 100[/latex] observations of Gaussian white noise, and
- two time series of [latex]n = 100[/latex] observations generated from a random walk, which were compared to a time series consisting of [latex]n = 100[/latex] closing values for the Dow Jones Industrial Average.
R has built-in data structures and functions that are useful in the analysis of a time series. Additional tools beyond just the plotting of a time series will be introduced subsequently.
It is often the case that we want to formulate a hypothetical population probability model for a time series from observed values of a time series, such as using the random walk model to model the Dow Jones Industrial Average closing values. This notion of formulating a population probability model is completely analogous to using the normal distribution to approximate the adult heights of Swedish women, for example. Once a tentative model has been identified, any unknown parameters are estimated and goodness-of-fit tests are conducted. After a fitted probability model is accepted as a reasonable population probability model to describe a time series, a wide variety of statistical inference procedures can be employed. Broad categories of these statistical inference procedures are listed and described in the next subsection.
7.1.2 Why Analyze a Time Series?
There is not one universal purpose for conducting a time series analysis. Some of the more common purposes for conducting a time series analysis include description, explanation, prediction, simulation, control, signal estimation, and segmentation. This list is not comprehensive, but certainly covers the vast majority of the applications of time series analysis.
- Description. Time series analysis is often useful for describing the time evolution of the observations in a time series. Plotting the values in the time series, as we have done in the four examples, is a critical first step for observing trends, seasonal effects, extreme observations, etc. The time series plot also allows an analyst to easily identify outliers in a time series and decide whether these outliers were due to a coding error that occurred when inputting the time series or just random extreme observations. More sophisticated techniques that are helpful in describing a time series, such as the sample autocorrelation function to detect and quantify serial dependence in the values of a time series, or the periodogram to detect and quantify cyclic variation in the values of a time series, will be introduced subsequently.
- Explanation. It is often the case that one time series can be used to explain another time series. The home energy consumption time series from Example 7.1, for instance, might be partially explained by a time series of monthly average outdoor temperatures in Williamsburg, Virginia in 2011–2018. Another time series that might partially explain the home energy consumption values is the average number of hours of daylight in Williamsburg in a particular month.
- Prediction. Certain application areas, such as quantitative finance and seismology, engage in the analysis of a time series for the purpose of forecasting. The prediction of the next value of the time series, or perhaps the value of the time series h time units into the future, is often of interest. In quantitative finance, predicting the future value of a particular stock based on its history to date might be of interest. In seismology, predicting the time of the next earthquake might be of interest. Forecasted values are typically given by a point estimate and an associated confidence interval that measures the precision of the point estimate.
- Simulation. Simulating a time series in a discrete-event simulation might be the ultimate goal. A time series model that adequately mimics the real-world time series is critical in building a valid simulation model. As an example of such a simulation, financial planners often turn to simulation to estimate the probability that an individual or a married couple will have enough money to pay their expenses in retirement. This simulation requires, among other elements, a time series model that is capable of generating the annual inflation rate over the lifetimes of the individual or couple. The generation of simulated future annual inflation rates is based on building a time series model from previous annual inflation rates. Other elements, such as annual stock market returns or interest rates, would require a separate time series model. The values in these various time series are often correlated.
- Control. Time series analysis can be performed with the goal of controlling a particular variable. Examples include keeping ball bearing diameters between two prescribed thresholds, keeping delivery times below a prescribed threshold, and keeping unemployment in an economy between two thresholds. A branch of quality control known as statistical process control refers to the time series plots given earlier as control charts.
- Signal estimation. Certain application areas, such as astrophysics and electrical engineering, are particularly interested in separating signal from noise. The techniques using spectral analysis, which is presented subsequently, are particularly adept at detecting cyclic variation in a time series. Sometimes a very weak signal can be detected in a very noisy time series using these techniques.
- Segmentation. Economists often find it useful to classify a period of economic activity as a period of expansion or a period of contraction. They do so by breaking a time series into a sequence of segments. The challenge here is to identify the boundary points at which times the economy switches from expansion to contraction and then back again. Determining these points in time in which the changes in the time series model occur is one of the goals of segmentation.
A time series is just one instance of a process that evolves randomly over time known as a stochastic process. The next section classifies stochastic processes based on whether time passes in a discrete or continuous fashion, and whether the variable of interest at each time step is discrete or continuous.
7.1.3 Where Does Time Series Analysis Fall in the Modeling Matrix?
The purpose of this subsection is to step back and consider where time series analysis fits in the larger arena of stochastic processes. The common elements between the four time series we have encountered so far are that time is measured as an integer (representing months for the first two time series, the first 100 positive integers for the Gaussian white noise, and trading days for the stock market averages) and the values of the time series observations are measured on a continuous scale. So a time series is a sequence of observed data values, measured on a continuous scale, which are collected over time. In most instances, the observations are taken at equally-spaced points in time. The observations in the time series are denoted generically by
and can be referred to more compactly as just [latex]\left\{ X_t \right\}[/latex]. Table 7.2 shows the position that time series analysis resides in the [latex]2 \times 2[/latex] table in which the nature of time (discrete or continuous) defines the rows and the nature of the observed variable (discrete or continuous) defines the columns. Time series analysis occupies the discrete-time, continuous-state entry in the table. Popular stochastic process models, such as Markov chains which are often used to model discrete-time and discrete-state stochastic processes, occupy the other three positions in the table.
|
state |
|||
|
discrete |
continuous |
||
|
time |
discrete |
Markov chains |
a time series model |
|
continuous |
continuous-time Markov chains |
Brownian motion |
|
The defining characteristic of a time series model is that time is measured on a discrete scale and the observations are measured on a continuous scale. You have seen four examples of time series. Here are examples of applications of stochastic models in the other three boxes in Table 7.2.
- The classic example of a discrete-time, discrete-state stochastic process with two states is the weather on a particular day. If the two states are “rainy” and “sunny” (actually “not rainy” should be the second state so as to partition the state space so that a cloudy day with no rain is classified as “not rainy”), then a Markov chain is a potential model for the evolution of the weather from one day to the next.
- A continuous-time, discrete-state stochastic process that we have all encountered is that of a single-server queueing system. The state of the system is the number of customers in the system. If the number of customers in the system can either go up by one (via a customer arrival) or down by one (via a customer departure), then the state of the system is discrete. Furthermore, since customer arrivals and departures can occur at any instant, time is measured on a continuous scale.
- One well-known example of a continuous-time, continuous-state stochastic process is Brownian motion, which is named after Scottish botanist Robert Brown (1753–1858). He described the motion in 1827 while observing the pollen of the plant Clarkia pulchella immersed in water through a microscope. Physicist Albert Einstein (1879–1955) explained that the motion of the pollen was caused by individual water molecules in 1905. Brownian motion can be thought of as a random walk in which the time between subsequent observations approaches zero.
Figure 7.6 contains a [latex]2 \times 2[/latex] array of graphs that are analogous to the [latex]2 \times 2[/latex] array of stochastic process models in Table 7.2. The values plotted are one particular realization, also known as a sample path, of a stochastic process. A stochastic process can be thought of as a probability model which evolves over time. The dashed lines indicate that time or state is measured discretely. In this sense, the techniques for analyzing a time series represent 25% of the techniques for analyzing all of the stochastic processes.
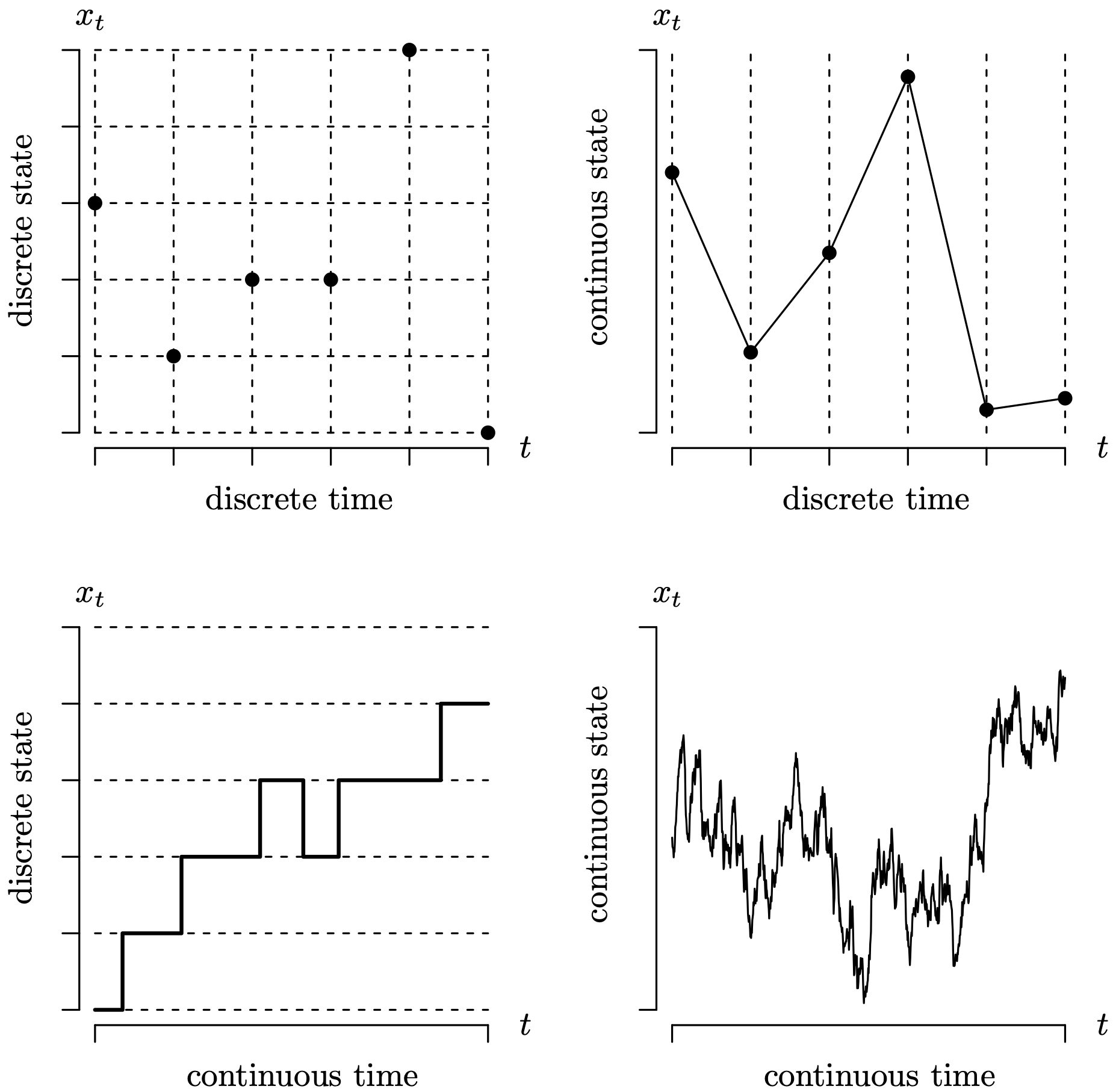
Long Description for Figure 7.6
The first graph shows the relation between discrete state and discrete time. The horizontal axis t and the vertical axis x subscript t have 6 tick marks each. Assuming the horizontal and the vertical axes meet at the origin, the points are plotted at (0, 3), (1, 1), (2, 2), (3, 2), (4, 5), and (5, 0). The second graph shows the relationship between continuous state and discrete time. The horizontal axis t has six tick marks. The vertical axis x subscript t is unmarked. The function initially decreases, then increases and reaches a peak at the fourth tick mark, decreases, and again increases. The third graph shows the relationship between discrete state and continuous time. The horizontal axis representing continuous time is unmarked. The vertical axis has 6 tick marks. The increasing step function has seven steps from the first to the fifth tick mark. Here, the fourth step is at the fourth tick mark, the fifth step is at the third tick mark, and the sixth step is at the fourth tick mark. The fourth graph shows the relationship between continuous state and continuous time. The horizontal axis t and the vertical axis x subscript t are unmarked. The graph begins with the mid value of continuous state, progressively decreases with many fluctuations, and then gradually increases to a peak.
7.1.4 Computing
We review some of the R functions that have been used in this section and also introduce some additional functions that are useful in time series analysis. All of these functions are available in the base distribution of R, so they are immediately available upon initiating an R session. These functions will typically be illustrated here for the built-in time series of monthly international air passenger counts from 1949 to 1960 named AirPassengers which was first encountered in Example 7.2, but they could be applied to any time series.
The time series function ts is used to convert data to the internal time series data structure in R. It takes arguments for the time series observations, the time of the first observation, the time of the last observation, the number of observations per unit of time, etc. As an illustration, the quarterly time series observations contained in the vector named data which begin in the second quarter of 1984 is converted to a time series named x via the ts function with the R command
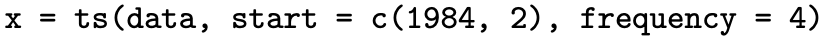
Once a time series is in the R time series data structure, the plot.ts function can be used to provide a plot of the time series, for example,

The ts.plot command can be used to plot several time series on a single set of axes, for example,
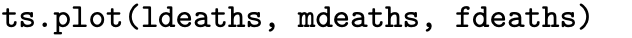
where the three time series that are built into R being plotted are monthly total deaths, male deaths, and female deaths from bronchitis, emphysema, and asthma in the United Kingdom from 1974 to 1979.
The next group of time series functions can be thought of as utilities, which are used to extract information about a time series. Illustrations of the application of these utility functions on the AirPassengers time series are given below.

The length function returns the length of a time series, which in this case is 144 observations. The start function returns the time associated with the first observation in the time series, which in this case is a vector comprised of the two elements 1949 and 1. The end function returns the time associated with the last observation in the time series. The frequency function shows the period length of a time series, which in this case is 12 because AirPassengers consists of monthly data. The deltat function returns the time increment associated with the time series, which in this case is [latex]1 / 12[/latex]. The time function returns the time values for each observation as a time series, which in this case is [latex]1949, \, 1949 \frac{1}{12} , \, 1949 \frac{2}{12} , \, \ldots , \, 1960 \frac{11}{12}[/latex]. The cycle function returns integers indicating the position of each observation in a cycle, which in this case is 12 iterations of the first 12 integers.
7.2 Basic Properties of a Time Series
A time series has some unique properties that will require some special tools to aid in its modeling and analysis. Central to these properties is the notion of stationarity, which is the subject of one of the subsections that follow. Once stationarity is established for a time series, then the population autocorrelation function, and its statistical counterpart, the sample autocorrelation function, can be helpful in characterizing a time series. These autocorrelation functions give the correlation as a function of the distance between the values in the time series. We begin by defining the population autocovariance and autocorrelation.
7.2.1 Population Autocovariance and Autocorrelation
Traditional statistical methods rely on the assumption that observations are mutually independent and identically distributed. In most practical time series applications, this assumption is violated because adjacent or nearby values in a time series are correlated. Thus, the special analysis tools for time series known as the population autocovariance function and the population autocorrelation function are introduced in this subsection. Before motivating and defining these new notions, we briefly review the definitions of population covariance and correlation from probability theory in the next paragraph. The link to time series analysis will be made subsequently.
The defining formula for the population covariance between the random variables X and Y is
where [latex]\mu_X = E[X][/latex] is the expected value of X and [latex]\mu_Y = E[Y][/latex] is the expected value of Y. The units on the population covariance are the units of X times the units of Y. When X and Y are independent random variables,
Zero covariance does not imply that X and Y are independent. The population correlation between the random variables X and Y is
where σX is the population standard deviation of X and σY is the population standard deviation of Y. The population correlation is a measure of the linear association between X and Y. The population correlation is unitless and satisfies [latex]-1 \le \rho \le 1[/latex], where the extremes indicate a perfect linear association.
A time series [latex]\left\{ X_t \right\}[/latex] consists of a sequence of observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] indexed over time. Since we are working with time series models rather than time series data values, the time series values will typically be set in uppercase in this subsection. The observations are continuous random variables that have been drawn from some population probability distribution. This probability distribution can be described by a joint probability density function
or an associated joint cumulative distribution function
The most well-known probability distribution for modeling n random variables [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] is the multivariate normal distribution, which is illustrated in the next example.
Although the multivariate normal distribution has some very appealing mathematical and statistical properties, it has one very significant drawback when it comes to being used as a time series model. That drawback concerns the number of parameters. There are n mean parameters [latex]\mu_1 , \, \mu_2, \, \ldots , \, \mu_n[/latex] and [latex]n (n + 1) / 2[/latex] parameters in the symmetric variance–covariance matrix [latex]\boldsymbol{\Sigma}[/latex]. If an analyst has collected just a single realization of a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], then there are many more parameters to estimate than data values. So one of the goals for the rest of the section is to establish properties of a time series which allow us to formulate parsimonious models that adequately model a particular time series with as few parameters as possible. We begin the process of establishing these properties by defining the population mean function and the population autocovariance function associated with a time series [latex]\left\{ X_t \right\}[/latex]. As you will see, the focus is on the first two population moments associated with the time series.
So as long as the observations in the time series have expected values that are finite, the population mean function gives the expected observed value of the time series at time t. In other words, the mean values
are the expected values of [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]. This defines what is essentially the first moment of the time series. The second moment of the time series is defined by the population autocovariance function.
Notice that the order associated with the arguments in the population autocovariance function is immaterial, so [latex]\gamma(s, \, t) = \gamma(t, \, s)[/latex]. Notice also that when the two arguments in the population autocovariance function are identical, the expression reduces to the population variance, that is,
The prefix “auto” means “self.” This prefix is attached to covariance to signify that the population covariance is being taken between two members of the same time series. The value of [latex]\gamma(s, \, t)[/latex] is the population covariance between two snapshots of the same time series at times s and t.
We now consider a sequence of three examples in which we (a) define a time series model, (b) calculate the population mean function, and (c) calculate the population autocovariance function. The three examples, which will be in order of increasing complexity, are
- white noise,
- a three-point moving average, and
- a random walk.
We begin with a process that consists of just white noise.
So the population mean and population autocovariance functions take on a particularly tractable form in the case of a time series that consists of white noise terms. We now consider calculating the population mean and population autocovariance functions for a three-point moving average of white noise.
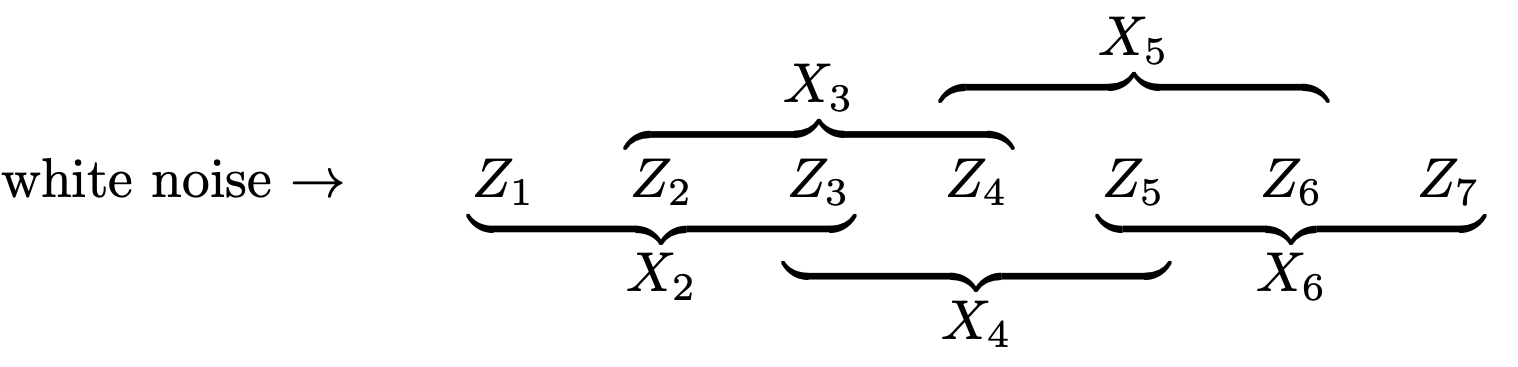
The third and final example concerns the calculation of the population mean function and the population autocovariance function for a random walk.
The three examples have illustrated how to find the population mean function and the population autocovariance function for a time series model. Sometimes the population autocorrelation function is also of interest because population correlation is unitless and always lies between [latex]-1[/latex] and 1. The population autocorrelation function is defined next.
We now revisit the previous three examples to compute the population autocorrelation function for the white noise, three-point moving average, and random walk models.
Although it lacks practical application in most real-world settings, the population autocorrelation function in the case of white noise is one of the most fundamental population autocorrelation functions possible. Since iid noise and Gaussian white noise are subsets of white noise, they also share this same population autocorrelation function. The next example considers the three-point moving average.
The third and final example concerns the calculation of the population autocorrelation function for a random walk model for a time series [latex]\left\{ X_t \right\}[/latex].
This ends the introduction to three important functions that are associated with a time series model:
- the population mean function [latex]\mu(t) = E \left[ X_t \right][/latex],
- the population autocovariance function [latex]\gamma(s, \, t) = \hbox{Cov} \left( X_s, \, X_t \right)[/latex], and
- the population autocorrelation function [latex]\rho(s, \, t) = \hbox{Corr} \left( X_s, \, X_t \right)[/latex].
An important property of a time series, known as stationarity, will be defined and illustrated in the next subsection. A stationary time series is one in which there is no long-term change in the probability mechanism governing the time series. Knowing that a time series is stationary will have an important effect on [latex]\mu(t)[/latex], [latex]\gamma(s, \, t)[/latex], and [latex]\rho(s, \, t)[/latex].
7.2.2 Stationarity
A time series [latex]\left\{ X_t \right\}[/latex] is stationary if the underlying probability mechanism that governs the time series is independent of a shift in time. In other words, if you select two different time windows in which to view a number of observations from the time series, the probability distribution of the observations in those two time windows will be identical.
A strictly stationary time series is also known as a strongly stationary or completely stationary time series. The next two examples contain the type of thought experiment that is appropriate for determining whether a time series is strictly stationary.
The discussion above would indicate that very few time series which occur in practice would be strictly stationary. The previous example asks whether a realization appears to be drawn from a stationary time series model. The next example gives a simple time series model which is strictly stationary.
So the international airline passengers data set, just from observing the time series, is not strictly stationary. The Gaussian white noise process is strictly stationary. There are several implications of a strictly stationary time series, some of which are listed below.
- The initial n values of the time series [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] and their associated observations shifted k time units to the left or right [latex]X_{k + 1}, \, X_{k + 2}, \, \ldots, \, X_{k + n}[/latex] having the same joint probability distribution implies that each must have the same joint cumulative distribution function, that is,
for all values of [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex].
- The marginal distribution of each value in the time series is identical. Symbolically,
for all integer time values s and t and all real-valued x.
- The population mean function [latex]\mu(t) = E \left[ X_t \right][/latex] is constant in time; that is, there is no trend.
- The population autocovariance function [latex]\gamma(s, \, t) = \hbox{Cov} \left( X_s, \, X_t \right)[/latex] is constant with respect to a shift; that is,
- Any time series consisting of mutually independent and identically distributed random variables must be strictly stationary.
Strict stationarity is a lot to ask of a time series, and is difficult to establish based on an observed realization of a time series. So time series analysts have defined a weaker version of strict stationarity which we will refer to here as just stationarity. Other terms used for this type of stationarity are
- weakly stationary,
- second-order stationary, and
- covariance stationary.
Whereas a strictly stationary time series required that the entire multivariate distribution remain the same on any time window, a stationary time series only places requirements on the first and second moments. The population mean function must be constant over time, and the population autocovariance function must depend only on the lag between the observations.
The first condition implies that the time series has no trend because each observation in the time series has the same expected value. The second condition implies that the population covariance between two observations is a function of only the absolute difference between the two time indexes of the observations. This second condition implies that a stationary time series model only requires a single argument, which is known as the lag k, when defining the population autocovariance and autocorrelation function. We will use the same names for these functions, but only use a single argument when the time series is stationary.
The population autocorrelation function for a stationary time series provides an important reflection of the structure of a time series model. It gives the modeler a view of how observations in the time series are correlated based on their distance away from one another in the time series. The next example relates the population correlation matrix and the population autocorrelation function for a time series model.
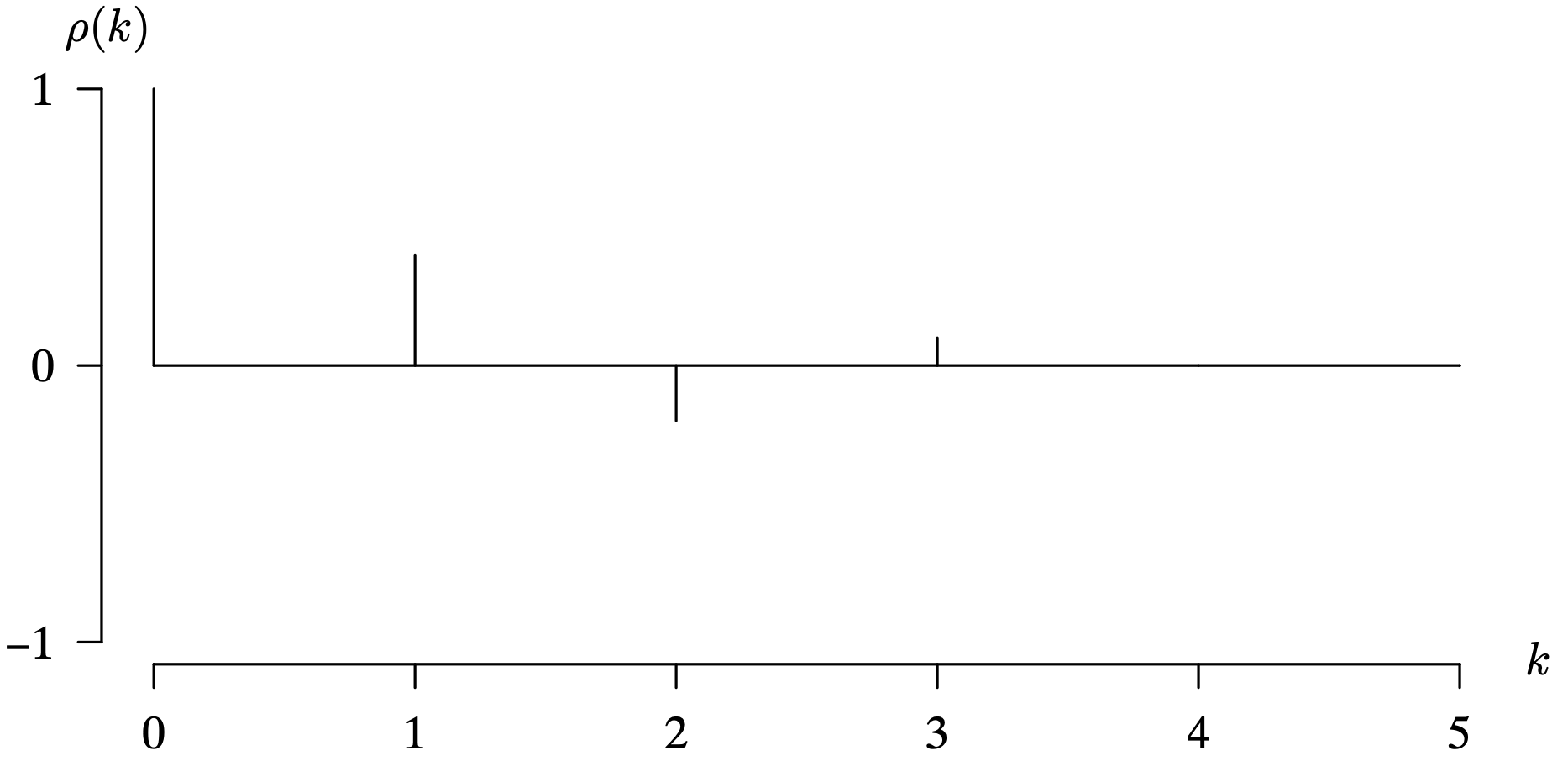
You might have noticed that the word population precedes autocorrelation function. This convention is not universal, but we do so in order to distinguish the population autocorrelation function from its statistical counterpart, the sample autocorrelation function. An analogy in the realm of univariate probability distributions is the distinction between the population mean μ, which is a constant, and its statistical counterpart, the sample mean [latex]\bar X[/latex], which is a random variable. In the same sense, the population autocorrelation function [latex]\rho(k)[/latex] is a sequence of population correlations, which are fixed constants that are indexed by the lag k. The sample autocorrelation function, which will be introduced in a subsequent section as rk, is a sequence of sample correlations, which are random variables that are indexed by the lag k.
Several properties of the population autocorrelation function for all stationary time series models are given next.
These properties of [latex]\rho(k)[/latex] have important implications in time series analysis. The first result from Theorem 7.1 indicates that there is perfect positive population autocorrelation between an observation and itself (that is, an observation at lag [latex]k = 0[/latex]). The initial spike in the population autocorrelation function at [latex]\rho(0) = 1[/latex] is generally included in a graph of the population autocorrelation function, although it conveys no information. The second result indicates that all population autocorrelation functions must lie between [latex]-1[/latex] and 1. Subsequent plots of [latex]\rho(k)[/latex] will always stretch the vertical axis from [latex]-1[/latex] to 1 so that they can easily be compared with one another. The third result indicates that [latex]\rho(k)[/latex] is an even function in k, so although k can be any integer, it is common practice to only graph [latex]\rho(k)[/latex] for [latex]k = 0, \, 1, \, 2, \, \ldots[/latex] because we know that the reflection about the [latex]\rho(k)[/latex] axis is identical. There is no need to graph the population autocorrelation function for negative lags because no additional information is conveyed. The fourth result explains why [latex]\rho(k)[/latex] tends to be more popular than [latex]\gamma(k)[/latex] because it is free of the units selected for Xt. The fifth result indicates that a time series model cannot be determined from its population autocorrelation function. Every stationary time series model has a population autocorrelation function, but knowing the autocorrelation function does not necessarily determine the underlying time series model.
We can now revisit the three examples from the previous subsection, namely white noise, a three-point moving average, and a random walk, to see if they are stationary time series models. In addition, we will make a plot of their population autocorrelation functions if they happen to be stationary.
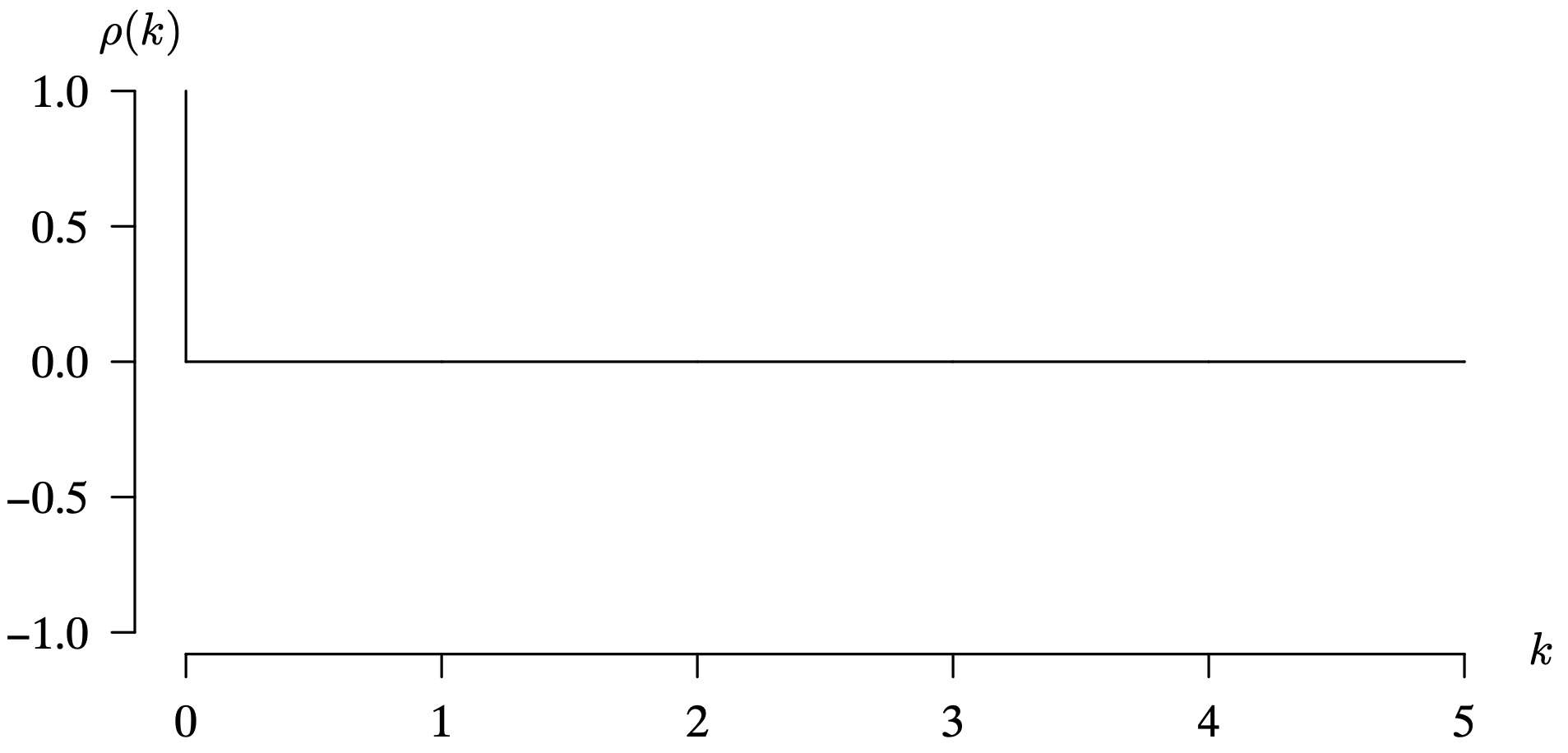
The population autocorrelation function for the white noise time series model is identical to that for iid noise and Gaussian white noise because those time series models are subsets of the white noise time series model. We now consider the three-point moving average model.
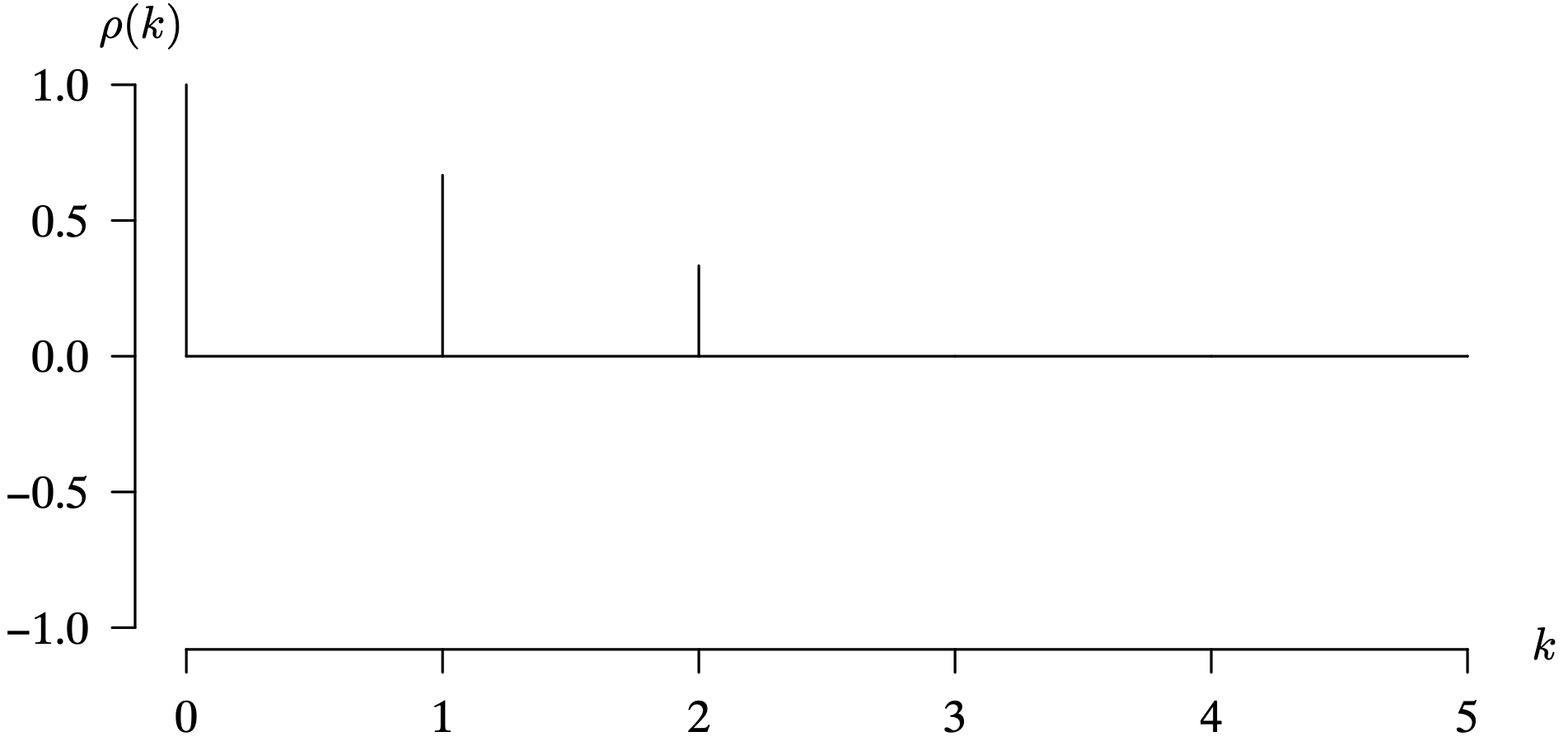
The previous example concerning a three-point moving average of white noise generalizes to an m-point moving average of white noise, where m is an odd, positive integer. The more general time series model is also stationary, and the population autocorrelation function also decreases linearly, and cuts off at lag m. The derivation of this result is given as an exercise at the end of this chapter. The third example considers a random walk time series model.
The statistical analogs of the population autocovariance and autocorrelation functions are the sample autocovariance and autocorrelation functions, which are calculated from an observed time series from a stationary model. These two functions are defined in the next subsection.
7.2.3 Sample Autocovariance and Autocorrelation
This section takes up the estimation of the population autocovariance function and the population autocorrelation function from a single realization of a time series denoted by the observations [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex]. In addition to the vital plot of a time series, a plot of the sample autocorrelation function, which is known as the correlogram, can yield additional insight concerning the underlying probability model governing the time series. The approach that we will take here is to review the sample versions of the covariance and correlation in terms of data pairs in the next paragraph, and then adapt these notions to their associated analogs in time series analysis.
This paragraph reviews the estimation of the population covariance and correlation from a data set of data pairs [latex](X_i, \, Y_i)[/latex], for [latex]i = 1, \, 2, \, \ldots, \, n[/latex]. The population covariance is estimated by the sample covariance
where [latex]\bar X[/latex] and [latex]\bar Y[/latex] are the sample means of the associated sample values:
This formula is the statistical analog to the formula
from probability theory. There are two formulas for estimating the population variance from a random sample—one with n in the denominator and one with [latex]n - 1[/latex] in the denominator. Since n is required to be fairly large in time series analysis, the choice between the two is not critical. The formula with [latex]n - 1[/latex] in the denominator is more prevalent in statistics because
for mutually independent and identically distributed observations [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex]; that is, the sample variance S2 is an unbiased estimator of the population variance [latex]\sigma _ X ^ {\, 2}[/latex]. We use n in the denominator here because, in spite of being a biased estimator of the population variance in the non-times-series setting, it leads to certain terms dropping out of a subsequent formula. The population variances can be estimated by the maximum likelihood estimators
An estimate for the population correlation ρ is given by the sample correlation
Notice that the [latex]1 / n[/latex] terms in the numerator and the denominator cancel. Had a denominator of [latex]n - 1[/latex], rather than n, been used in the formulas for [latex]\widehat {\hbox{Cov}} (X, \, Y)[/latex], [latex]\hat{\sigma} _ X ^ {\, 2}[/latex], and [latex]\hat{\sigma} _ Y ^ {\, 2}[/latex], the same cancellation would occur. Table 7.3 summarizes the results from Section 7.2.1 and this paragraph.
|
covariance |
correlation |
|
|---|---|---|
|
population |
$$E \left[ ( X - \mu_X ) ( Y - \mu_Y) \right]$$ |
$$\displaystyle{\frac{E \left[ \left( X - \mu_X \right) |
|
sample |
$$\genfrac{}{}{0pt}{}{}{\displaystyle{\frac{1}{n} \sum_{i\,=\,1}^n |
$$\displaystyle{\frac{ |
We now translate the concepts from the previous paragraph into the context of the analysis of a time series. Consider the estimation of [latex]\gamma(k)[/latex] and [latex]\rho(k)[/latex] from a realization of observations [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], which are assumed to be observed values from a stationary time series model. The lag k sample autocovariance, which estimates [latex]\gamma(k)[/latex], is
where [latex]\bar x[/latex] is the sample mean of the observations in the time series. This is not a universal choice for ck. Since there are [latex]n - k[/latex] terms in the summation, some time series analysts prefer to divide by [latex]n - k[/latex] rather than n. Because of the two different options for the denominator, it is important to only calculate ck for k values that are significantly smaller than n. Generally speaking, there should be at least 60 to 70 observations in a time series to use the techniques described here. Having a large value of n means that having n or [latex]n - k[/latex] in the denominator is not critical for small values of k. The units on ck are the square of the units of the observations in the time series. Notice that when [latex]k = 0[/latex], the lag 0 sample autocovariance reduces to
which is an estimate for [latex]\gamma(0) = \sigma _ X ^ {\, 2}[/latex]. The lag k sample autocorrelation, which estimates [latex]\rho(k)[/latex], is
for integer values of k which are significantly smaller than n. As was the case with [latex]\rho(k)[/latex], the lag k sample autocorrelation is a unitless quantity. When [latex]k = 0[/latex], [latex]r_0 = c_0 / c_0 = 1[/latex], as desired. The notation developed here to calculate [latex]\gamma(k)[/latex] and [latex]\rho(k)[/latex] for a stationary time series model and to estimate these functions with ck and rk for an observed time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] is summarized in Table 7.4.
|
lag k autocovariance |
lag k autocorrelation |
|
|---|---|---|
|
population |
[latex]\displaystyle{\gamma(k) = E \left[ \left( X_t - \mu_X \right) \left( X_{t + k} - \mu_X \right) \right]}[/latex] |
[latex]\displaystyle{\rho(k) = \frac{\gamma(k)}{\gamma(0)}}[/latex] |
|
sample |
[latex]\displaystyle{c_k = \frac{1}{n} \sum_{t\,=\,1}^{n - k} \left( x_t - \bar x \right) \left( x_{t + k} - \bar x \right)}[/latex] |
[latex]\displaystyle{r_k = \frac{c_k}{c_0}}[/latex] |
Computing Sample Autocovariance and Autocorrelation
We now consider the estimation of the lag k sample autocovariance ck and the lag k sample autocorrelation rk in R. We write an R function named autocovariance below that has two arguments: the vector containing the time series x and the lag k. The first statement in the function uses the length function to determine the number of observations in the time series. The second statement uses the mean function to calculate the sample mean of the values in the time series. The third statement uses the formula
to calculate the lag k sample autocovariance.
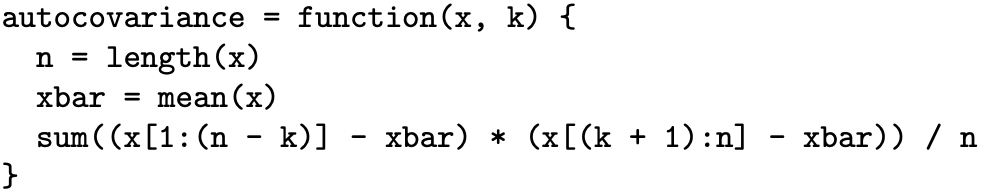
We can now write an R function named autocorrelation below that has the same arguments as the autocovariance function. It uses the formula
to calculate the lag k sample autocorrelation.

Time series analysts typically plot the sample autocorrelation function values for the first few lags. This plot is known as either the sample autocorrelation function or the correlogram. We illustrate the calculation and plotting of the correlogram for a simulated time series whose elements are Gaussian white noise, so [latex]\sigma _ X = \sigma _ Z[/latex]. Recall that Gaussian white noise, denoted by
consists of mutually independent [latex]N\left( 0, \, \sigma_Z ^ {\, 2} \right)[/latex] observations. Recall from Example 7.15 that the population autocovariance function is
and the population autocorrelation function is
We expect the sample autocorrelation function to be similar to the population autocorrelation function except for random sampling variability. The R code below plots the correlogram for the first 20 lags for a time series that consists of [latex]n = 100[/latex] observations of a Gaussian white noise time series. We have assumed here that the population variance of the Gaussian white noise is equal to one (that is, [latex]\sigma_Z = 1[/latex]). The first statement in the R code below uses the set.seed function to set the random number seed to 8. The second statement uses the rnorm function to generate a time series consisting of 100 mutually independent standard normal random variates. The vector correlogram is initialized to a vector of length 21. This will hold the lag 0 sample autocorrelation function value (which is always [latex]r_0 = 1[/latex]) and the sample autocorrelation function values for lags 1 to 20. The autocorrelation function defined previously will compute the sample autocorrelation values. Finally, the plot function is used to plot the sample autocorrelation function. Using the type = "h" argument in the call to plot graphs the sample autocorrelation values as spikes. This is largely a matter of personal taste. Some time series analysts prefer to connect them with a line. We take the spike approach to emphasize that a non-integer value for the lag has no meaning in the context described here. The ylim = c(-1, 1) argument is included so that the entire potential range of the sample autocorrelation values [latex]-1 \le r_k \le 1[/latex] is included. The abline function is used to draw a horizontal line at [latex]r_k = 0[/latex], and two other dashed lines that will be described subsequently.

The plot of the time series and the correlogram for the first 20 lags are given in Figure 7.12. The time series plot displays the typical pattern for Gaussian white noise. The observations are mutually independent, so equally likely to be positive or negative. There are just a handful of observations more than 2 units away from the population mean function [latex]\mu(t) = E[X_t] = 0[/latex]. The correlogram is exactly what we anticipated for a time series consisting of Gaussian white noise based on our population autocorrelation function [latex]\rho(k)[/latex], which was one at lag zero and zero at all other lags. We have [latex]r_0 = 1[/latex], as expected, and then small spikes associated with values of rk at other lag values k that reflect the random sampling variability in the specific time series values that were generated by the rnorm function. The correlogram has a horizontal line drawn at correlation 0 to make it clearer which spikes are positive and which are negative. In addition, the correlogram would be identical if all of the points in the time series were translated to have arbitrary population mean μ rather than population mean 0. Correlograms are not influenced by a shift in the time series. Since drawing a correlogram occurs so frequently in the analysis of a time series, R has automated the process with the acf function (acf is an abbreviation for autocorrelation function). After a call to set.seed(8), all of the previous calculations can be performed with the single R statement
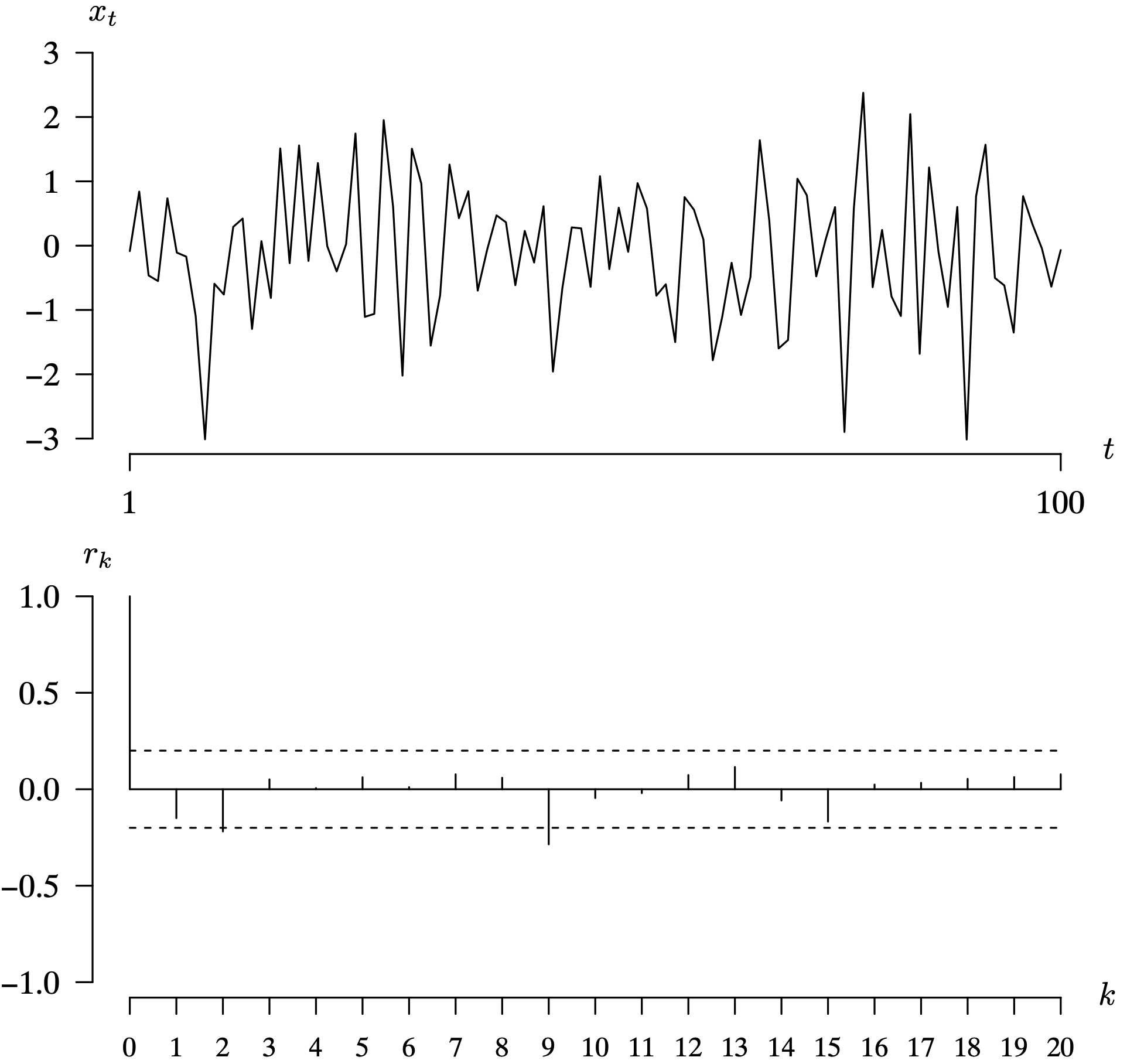
Long Description for Figure 7.12
In the time series plot, the horizontal axis t ranges from 0 to 100. The vertical axis measures x subscript t and ranges from negative 3 to 3 in increments of 1 unit. The noise value at time t equals 1 is 0, fluctuates, and reaches a minimum of negative 3 at t equals 10. It then increases and vacillates between negative 2 and 2 from t equals 15 to 75, reaching a maximum value of 2.3 at t equals 79 and a minimum value of negative 3.015 at t equals 90. All data are estimated. In the correlogram, the horizontal axis k ranges from 0 to 20 in increments of 1 unit. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A solid horizontal line is drawn at 0.0. The dashed horizontal lines are drawn at the r subscript k values negative 0.2 and 0.2. The r subscript k values for the first 20 lags are negative 0.15, negative 0.2, 0.05, 0.01, 0.05, 0.01, 0.05, 0.04, negative 0.25, negative 0.02, negative 0.01, 0.05, 0.015, negative 0.05, negative 0.2, 0.01, 0.02, 0.05, 0.05, and 0.08. All data are estimated.
When you make this call to the acf function, you will notice that two dashed lines are drawn just above and just below the horizontal line [latex]r_k = 0[/latex], as was the case in Figure 7.12. These two lines are 95% confidence limits that are helpful for determining whether the sample autocorrelation function values are statistically different from zero. Even for a time series consisting of Gaussian white noise, the probability distribution of rk is complicated because the formula for rk is complicated. However, when the time series [latex]\left\{ X_t \right\}[/latex] consists of mutually independent observations, the population mean and variance of rk are
and
for [latex]k = 1, \, 2, \, \ldots[/latex], and these values are asymptotically normally distributed. This means that an approximate two-sided 95% confidence interval for rk when n is large and k is significantly less than n is
where 1.96 is the 0.975 fractile of the standard normal distribution. Since n is typically large in time series analysis, the [latex]1 / n[/latex] term is often assumed to be small enough to ignore. Furthermore, if 1.96 is rounded to 2, then this approximate 95% confidence interval simplifies to
The limits at [latex]\pm 2 / \sqrt{n}[/latex] are plotted in Figure 7.12 as dashed lines at [latex]\pm 2 / \sqrt{100} = \pm 0.2[/latex]. We notice that the spikes in the correlogram in Figure 7.12 fall outside of the confidence interval limits for lag 2 (just barely) and lag 9. We should not be concerned about this occurring. Since these are approximate 95% confidence intervals, we would expect to have about 1 in 20 values fall outside of the limits even if we had mutually independent observations in the time series. Since it appears that there is little or no pattern to the spikes in Figure 7.12, we conclude that the two spikes that exceeded the confidence limits are just due to random sampling variability. Significant spikes at lower lags, for example, lag 1 and lag 2 should be scrutinized more carefully than other lone significant spikes, such as the one that we saw at lag 9. Furthermore, a significant spike at a lag associated with possible seasonal variation (for example, lag 12 for monthly data with a suspected annual variation) should also be scrutinized more carefully than other statistically significant spikes.
Correlogram Examples
Experience is critical in interpreting correlograms. Four examples are given here to illustrate the recommended thought process associated with the interpretation of a time series and its correlogram. The four examples are
- a time series with a linear trend illustrated by the population of Australia from 1971–1993,
- a time series of the first 100 Dow Jones Industrial Average closing values in the year 2000,
- a time series of chemical yields, and
- a seasonal time series illustrated by the home energy consumption values from 2011–2018.
For all four time series, we (a) plot the time series, (b) plot the associated correlogram, (c) interpret the statistically significant spikes in the correlogram, and (d) interpret the shape of the spikes in the correlogram.
The next example considers a time series that has statistically significant positive autocorrelation values at small lags.
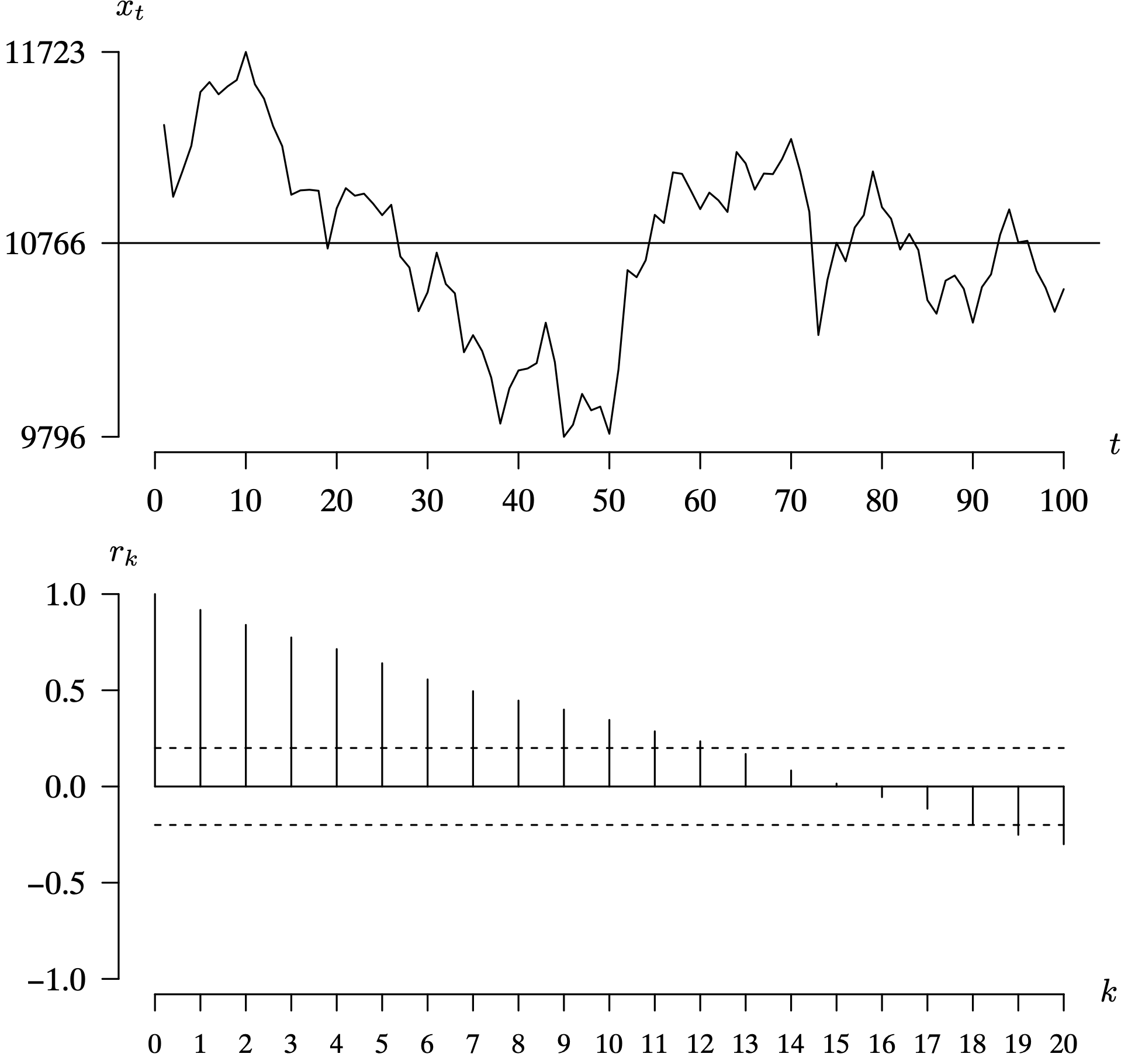
Long Description for Figure 7.14
In the time series plot, the horizontal axis t ranges from 0 to 100 in increments of 10 units. The vertical axis x subscript t ranges from 9796 to 11723. A horizontal line is at the x subscript t value 10766. The function begins above the horizontal line, reaches a peak of 11723 at t equals 10, and then progressively decreases to a low point of 9796 at t equals 40 and 50. It then increases gradually to 11000, then decreases and vacillates around the horizontal line. In the correlogram, the horizontal axis k ranges from 0 to 20 in increments of 1 unit. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The dashed horizontal lines are drawn at the r subscript k values negative 0.2 and 0.2. The r subscript k values are positive for k equals 0 through 15. The values progressively decrease from 1.0 to 0.02. The r subscript k values are negative for k values 16 through 20, and the values decrease from negative 0.03 to negative 0.3 All data are estimated.
The next example considers a stationary time series in which adjacent observations tend to be on opposite sides of the sample mean.
The final example illustrates the impact of a time series with a seasonal component on the shape of the correlogram.
To summarize the section thus far, the population mean function [latex]\mu(t) = E \left[ X_t \right][/latex] is the expected value of the time series at time t, and indicates whether a trend and/or cyclic variation is present. The population autocovariance and population autocorrelation functions reflect the linear relationship between two values, Xs and Xt, in the time series. A time series is stationary if the population mean function is constant in t and the population autocovariance function [latex]\gamma(s, t) = \hbox{Cov} \left( X_s, \, X_t \right)[/latex] depends only on [latex]|t - s|[/latex]. For a stationary time series, the population autocovariance function and the population autocorrelation function can be written as a function of the lag [latex]k = |t - s|[/latex] as [latex]\gamma(k)[/latex] and [latex]\rho(k)[/latex]. The sample autocorrelation function estimates the population autocorrelation function.
Occasions arise in time series analysis in which we are also interested in the correlation between Xt and [latex]X_{t + k}[/latex] with the linear dependency on the values between these two values, namely [latex]X_{t + 1}, \, X_{t + 2} , \, \ldots , \, X_{t + k - 1}[/latex], removed. This leads to what is known as the partial autocorrelation function, which is presented next.
7.2.4 Population Partial Autocorrelation
One key characteristic of nearly all time series is that nearby observations tend to be correlated. This makes the notion of autocorrelation crucial in time series analysis because it captures the correlation between observations in a stationary time series that are separated in time by a prescribed number of lags. The population autocorrelation function was introduced in Section 7.2.1; its statistical counterpart, the sample autocorrelation function, was introduced in Section 7.2.3.
It is often difficult to distinguish between population autocorrelation functions for two different competing, tentative stationary time series models in practice because
- the population autocorrelation functions for the two models are nearly identical, and/or
- there is significant sampling variability in the sample autocorrelation functions making it difficult to determine which of the two models provides a better fitted model.
As will be seen in subsequently, the sample autocorrelation function is particularly helpful for determining the number of terms to include in a popular time series model known as a moving average model. However, the sample autocorrelation function is much less helpful for determining the number of terms to include in another popular time series model known as an autoregressive model. A second type of autocorrelation function, the partial autocorrelation function, is an ancillary diagnostic tool to help determine the number of terms to include in an autoregressive model. As was the case with the autocorrelation function, there is a population and a sample version of the partial autocorrelation function. The population partial autocorrelation function is introduced in this subsection.
The notion behind partial autocorrelation is intuitive. Before describing the interpretation of partial autocorrelation in the context of time series analysis, we present a scenario involving just partial correlation in a more general setting. Let's say you are interested in the correlation between a full-time employee's age, X, and their annual income, Y. Intuition suggests that this correlation is positive because annual income tends to rise with age. But there are other factors that influence income, such as the employee's education level achieved, the number of years on the job, specific industry of employment, etc. To simplify, let's consider just one of these factors, say, the employee's years of education achieved, Z. The population partial correlation is the population correlation between age X and annual income Y with the linear relationship associated with the number of years of education Z removed. We are effectively controlling for the influence of education as we measure the correlation between X and Y. We regress X on Z to obtain [latex]\tilde X[/latex]. We regress Y on Z to obtain [latex]\tilde Y[/latex]. This regression is in the sense of probability rather than its statistical counterpart (which typically uses least squares for parameter estimation). Finally, we calculate the population partial correlation [latex]\hbox{Corr} \left( X - \tilde X, Y - \tilde Y \right)[/latex], which is the population correlation between X and Y with the linear influence of Z removed. Like the ordinary population correlation, the population partial correlation falls in the closed interval [latex][-1, \, 1][/latex]. The extreme values on this interval correspond to perfect negative population correlation and perfect positive population correlation, respectively. To summarize, the partial correlation measures the degree of linear association between two variables, with the linear association of one or more other variables removed.
Returning to the time series context, the partial autocorrelation reflects the relationship between observations at a particular lag in a time series with the linear relationship associated with intervening observations removed. The variables whose influence is being removed are the observations between the two values of the time series of interest. Stated in another fashion, the partial autocorrelation at lag k is the population correlation between two observations in the time series that are k time units apart after the removal of the linear influence of the time series observations at lags [latex]1, \, 2, \, \ldots , \, {k - 1}[/latex]. As was the case with autocorrelation, we want to find the population and sample versions of the partial autocorrelation. We will then have an inventory of possible population partial autocorrelation shapes that we can match to sample partial autocorrelation functions, which will help determine the number of terms to include in a time series model. The main role of the sample partial autocorrelation function is to determine the number of terms to include in an autoregressive model.
We now develop some general notation concerning partial autocorrelation. Although many authors use [latex]\phi_{kk}[/latex] to denote the population lag k partial autocorrelation, we will instead use [latex]\rho ^ * (k)[/latex] to emphasize that this quantity is still a correlation and to use the symbol [latex]\phi[/latex] exclusively for the coefficients in an autoregressive time series model. The superscript * is used to distinguish the population partial autocorrelation function from the population autocorrelation function [latex]\rho(k)[/latex]. Likewise, we will use [latex]r^*_k[/latex] to denote the sample lag k partial autocorrelation in the next subsection. The superscript * is used here to distinguish the sample partial autocorrelation function from the sample autocorrelation function rk.
The next example illustrates the calculation of a population partial autocorrelation for a stationary time series model.
We now pivot from the calculation of population partial autocorrelation for a specific time series model to the calculation of the population partial autocorrelation for a general stationary time series model. Let's begin with the calculation of the lag 1 population partial autocorrelation [latex]\rho ^ * (1)[/latex] for a stationary time series model. By definition, this is the population correlation between Xt and [latex]X_{t - 1}[/latex] after removing the linear effect of any observations between Xt and [latex]X_{t - 1}[/latex]. But there aren't any observations between Xt and [latex]X_{t - 1}[/latex], so the lag 1 population partial autocorrelation is simply the lag 1 population autocorrelation: [latex]\rho ^ * (1) = \rho(1)[/latex]. The population partial autocorrelation for higher lags uses the best linear estimate of each of the two values of interest as a function of the intervening values. Minimizing the associated mean square error, the population partial autocorrelation can be determined by solving a set of linear equations. Using Cramer's rule to solve these equations, the population lag 2 partial autocorrelation function value is given by the ratio of determinants
Notice that the denominator is the determinant of the correlation matrix of any two adjacent observations. The numerator is the determinant of this same matrix with the last column replaced by the first two population autocorrelation values. This pattern continues for the population lag 3 partial autocorrelation function value, which is
Again, the denominator is the determinant of the correlation matrix of any three sequential observations. The numerator is the determinant of this same matrix with the last column replaced by the first three population autocorrelation values (where the lag number matches the row number). This pattern continues for higher lag values, which leads to the following definition.
The next example illustrates the calculation of the population partial autocorrelation function for a stationary time series model.
7.2.5 Sample Partial Autocorrelation
We now transition from considering the population partial autocorrelation function to considering its statistical counterpart, the sample partial autocorrelation function. Calculating the sample partial autocorrelation function is just a matter of replacing the population values with the sample values in the determinants given in Definition 7.8.
Given an observed time series, the R code from the previous example that used the det function to calculate the determinants could be used to perform these calculations. The sample partial autocorrelation function can be calculated much more efficiently, however, by using the built-in pacf function in R, as illustrated in the next example. The lag in which the sample partial autocorrelation function values become statistically indistinguishable from zero can be determined by using the approximate result that for a time series of white noise values, [latex]r^*_k \sim N\left( 0, \, 1 / n \right)[/latex], for [latex]k = 1, \, 2, \, \ldots[/latex]. For this reason, the pacf function in R plots dashed lines at the approximate 95% bands at [latex]\pm 1.96 / \sqrt{n}[/latex]. These dashed lines are useful to a time series analyst in determining which sample partial autocorrelation values differ significantly from zero.
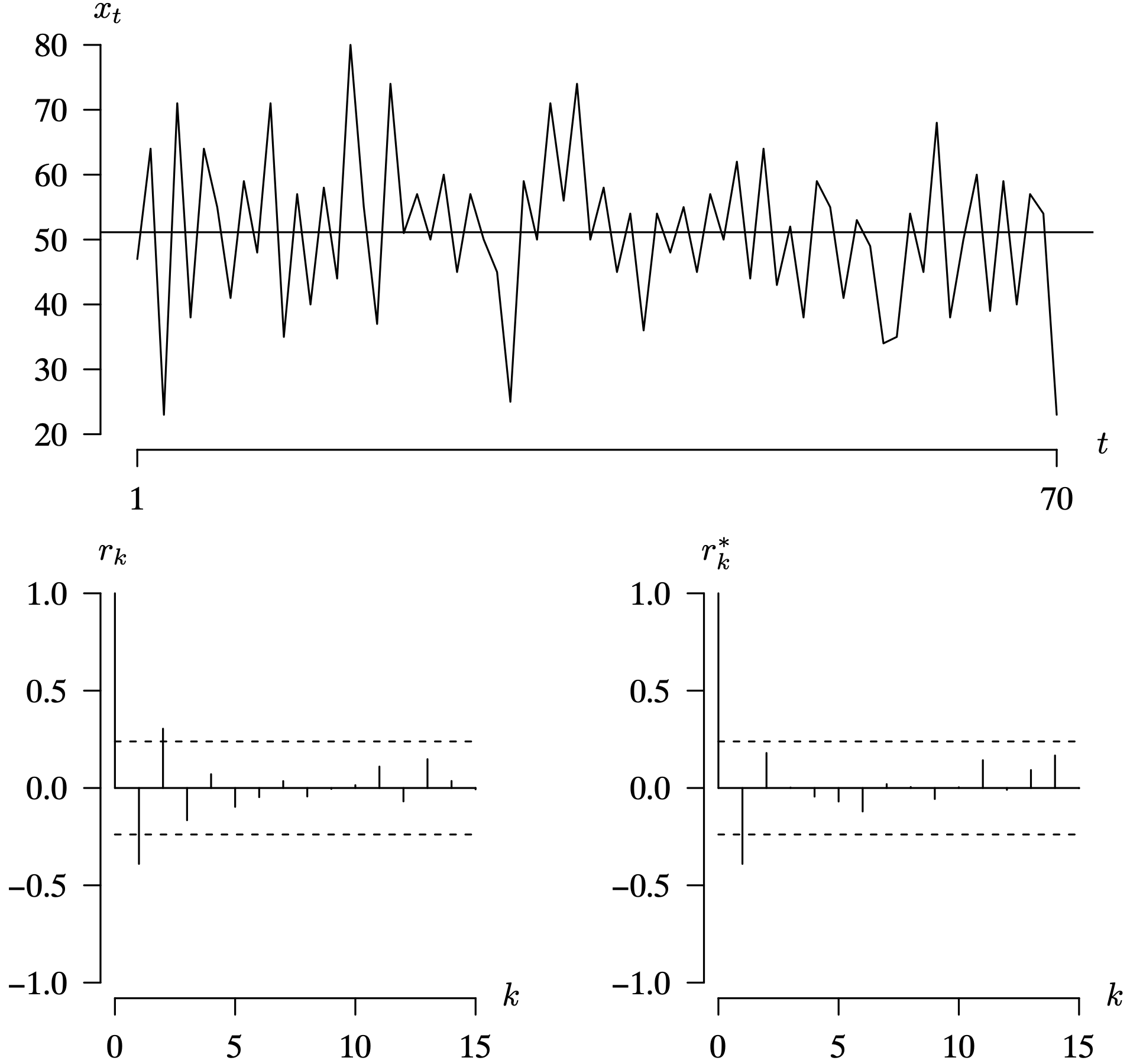
Long Description for Figure 7.18
In the time series plot, the horizontal axis t ranges from 1 to 70. The vertical axis x subscript t ranges from 20 to 80 in increments of 10 units. A horizontal line is at the x subscript t value 51. The function begins below the horizontal line, reaches a minimum of 23 at t equals 3, then increases, vacillates around the horizontal line between 35 and 70, and peaks with 80 at t equals 17. It then progressively decreases to 25 at t equals 29, increases, vacillates between 35 and 60 until t equals 69, and again decreases to a minimum of 23 at t equals 70. In the first correlogram, the horizontal axis k ranges from 0 to 15 in increments of 1 unit. The vertical axis r subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A solid horizontal line is drawn at 0.0. The dashed horizontal lines are drawn at r subscript k values negative 0.2 and 0.2. The r subscript k values for k equals 1 to 15 are negative 0.35, 0.3, negative 0.15, 0.05, negative 0.1, negative 0.02, 0.01, negative 0.01, 0, 0, 0.1, negative 0.05, 0.2, and 0.1, respectively. In the second correlogram, the horizontal axis k ranges from 0 to 15 in increments of 5 units. The vertical axis r star subscript k ranges from negative 1.0 to 1.0 in increments of 0.5 units. A horizontal line is drawn at 0.0. The values of r star subscript k for k values 0 to 15 are 1.0, negative 0.4, 0.2, negative 0.05, negative 0.1, negative 0.2, 0.05, 0, negative 0.1, 0.15, negative 0.01, 0.1, and 0.2, respectively. All data are estimated.
There will be more examples of computing the partial autocorrelation function and its interpretation subsequently.
7.2.6 Computing
The R plot.ts function generates a plot of a realization of a time series, which is an important initial step in formulating an appropriate stochastic model for the time series. Many time series analysts prefer to also see the sample autocorrelation and partial autocorrelation functions along with the plot of the time series. The layout function can be used to stretch the plot of the time series horizontally, while horizontally compressing the plots of the sample autocorrelation and partial autocorrelation functions. The acf function computes the sample autocorrelation function and has arguments that control the number of lags to display, whether to suppress the plot, etc. The pacf function computes the sample partial autocorrelation function and has similar arguments. Notice that the acf function includes the lag 0 sample autocorrelation, which is always 1, but the pacf function does not include the lag 0 sample partial autocorrelation. The statements below apply these functions to the built-in R AirPassengers time series.

The vertical axes on all three plots are autoscaled. Use the ylim = c(-1, 1) argument in the acf and pacf functions in order to stretch the vertical axis from [latex]-1[/latex] to 1. Finally, the ARMAacf function can be used to compute the population autocorrelation and partial autocorrelation function values for a prescribed time series model.
7.3 Operations on a Time Series
This section considers operations that can be performed on a time series. The first subsection introduces filters that can be applied to a time series. We have already encountered an example of a filter when we considered a three-point moving average of a time series consisting of Gaussian white noise. The second subsection introduces decomposition, which is the process of breaking an observed time series into its component parts. The AirPassengers time series that is built into R, for example, can be decomposed into an trend, a seasonal component, and any remaining noise in the process once the trend and seasonal components have been removed. The third subsection concerns R functions that can be helpful in implementing these operations.
7.3.1 Filtering
This section takes up the important topic of filtering, which can be thought of as the process of converting one observed time series [latex]\left\{ x_t \right\}[/latex] to another time series [latex]\left\{ y_t \right\}[/latex]. The mathematical operations required to convert one time series to another can be abstractly depicted as
It is often the case that several of these filters can be applied sequentially to a particular observed time series. Filter 1, for example, converts [latex]\left\{ x_t \right\}[/latex] to [latex]\left\{ y_t \right\}[/latex], and then Filter 2 converts [latex]\left\{ y_t \right\}[/latex] to [latex]\left\{ z_t \right\}[/latex].
The resultant time series [latex]\left\{ z_t \right\}[/latex] is not associated with the white noise terms Zt from Definition 7.1. The purpose of such a series of filters applied to a time series might be to remove the trend with the first filter, and then to remove some seasonal variation with the second filter. If the resulting time series [latex]\left\{ z_t \right\}[/latex] looks like random noise values, then the two filters applied in series have successfully removed the trend and the seasonal variation.
Three different general classes of filters will be considered: transformations, detrending, and linear filters. These classes of filters allow for the manipulation of a times series for a particular purpose, such as smoothing or variance stabilization.
Transformations
One simple filter that can be applied to a time series is to apply a transformation to each element of the time series. Two transformations that are commonly applied to a time series are the logarithmic and square root transformations, which are
and
Some common purposes of applying such a transformation are to
- stabilize the variance of the time series (for example, when larger values of xt tend to have greater variability than smaller values of xt),
- make the trend and seasonal components of a time series appear to be additive, rather than multiplicative, in nature, and
- make the values in the filtered time series appear to be similar to white noise, iid noise, or Gaussian white noise (see Definition 7.1). The advantage to having values of the fitted time series be approximately mutually independent and normally distributed is to enable the use of easier statistical inference procedures concerning, for example, forecasted values.
The transformation of the values in a time series given in the next example is a variance-stabilizing transformation which makes significant improvement to a time series in terms of its visualization and interpretation.
Detrending Filters
When a consistent trend in a time series is apparent, as was the case with the international airline passengers time series from Example 7.2, an analyst typically would like to estimate the trend. Once the trend has been estimated, the residual time series remaining after detrending can often be fitted to a time series model. There are two popular types of filters that can be used to detrend a time series: curve fitting and differencing. These will be considered individually. Time series analysts often use the term secular trend to describe a long-term, non-periodic trend, but we will refer to it as just a trend here.
One way to detrend a time series is to fit a curve that approximates the mean value of the time series. As a simple example, consider a time series that appears to have a linear trend. In this case a simple linear regression statistical model
can be fitted to the time series in order to estimate the slope β0 and intercept β1 of the regression line. The time t plays the role of the predictor in the regression model; the time series observations Xt play the role of the response in the regression model. It is also possible to have a non-linear trend in a time series. A quadratic trend in time, for example, could be modeled via
Note that this model is linear in the β parameters. The statistical models used to detrend a time series are not limited to just polynomials in time. It is also possible to have an exponential model such as
This model is not linear in the β parameters. The potential statistical models are endless. A working knowledge of regression modeling is helpful in constructing an appropriate model for formulating, estimating, and assessing a model for the trend in a time series.
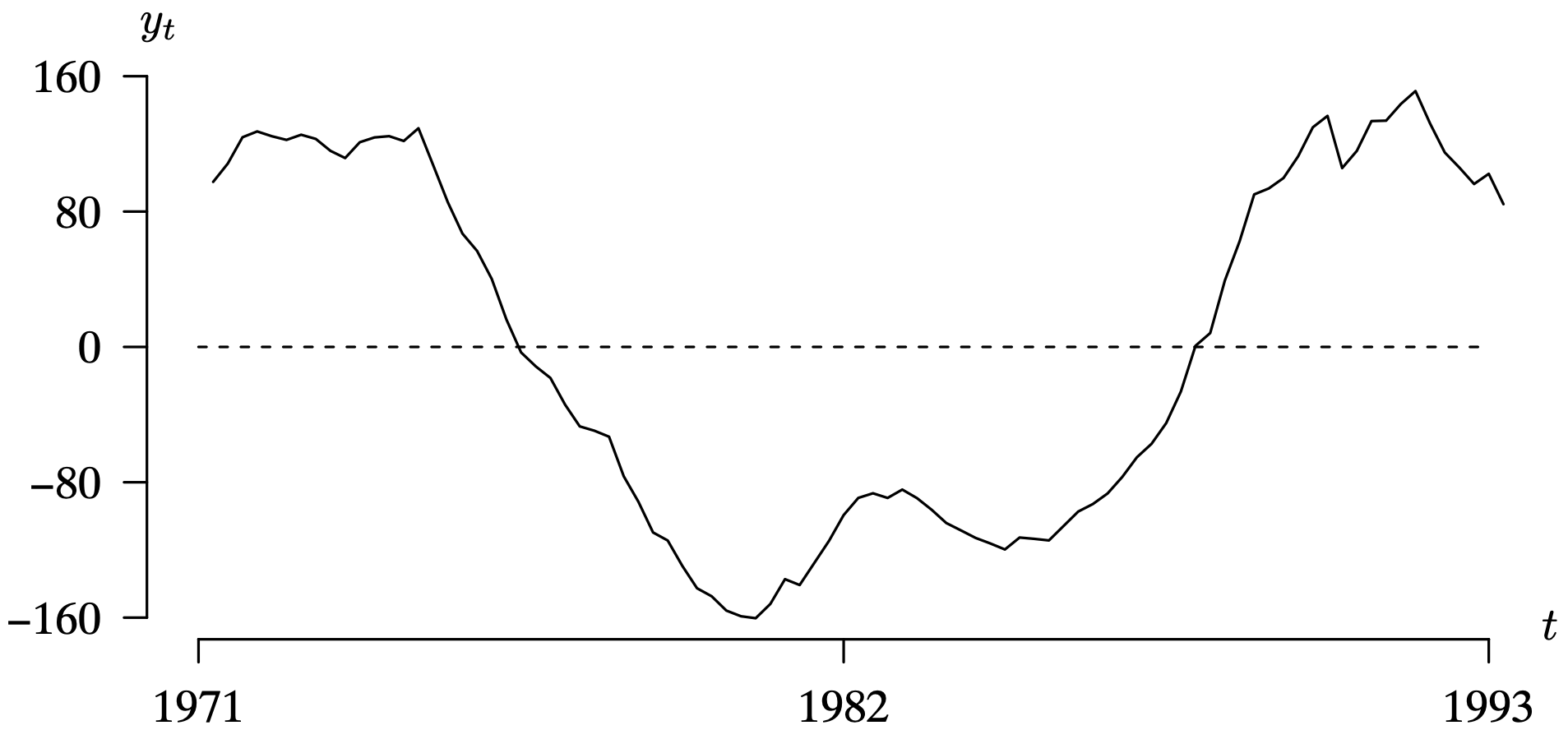
Long Description for Figure 7.23
The horizontal axis t lists years from 1971 to 1993 in increments of 11 years. The vertical axis y subscript t represents the population and ranges from negative 160 to 160 in increments of 80 units. A dashed horizontal line is drawn at y subscript t equals 0. The population of Australia vacillates around about 100 to 120 from the year 1971 to 1975, then decreases to negative 160 in 1980, again increases to negative 80 in 1983, and then decreases to negative 120 in 1986. It then progressively increases to a peak of 145 in the year 1992 and decreases to 80 in 1993. All data are estimated.
A second way to detrend a time series is to use differencing. The difference operator ∇, is defined as a filter by
where B is the backshift operator defined by [latex]Bx_t = x_{t - 1}[/latex]. Differencing a time series is the discrete analog of taking a derivative of a continuous function. So a time series that exhibits a linear trend, for example, will pass through the differencing filter ∇ and result in a time series without a trend. Notice that there will be one fewer observation in the new time series after applying this filter. If the original time series observations are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], then the differenced series will be [latex]y_2, \, y_3, \, \ldots, \, y_n[/latex]. Likewise, a time series with a quadratic trend can be detrended by applying the differencing operator ∇ twice to the original time series:
This detrending filter can be written with the backshift operator as [latex]y_t = (1 - 2B + B ^ 2) x_t[/latex]. There will be two fewer observations in the new time series after applying this filter. If the original time series observations are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], then the twice differenced series will be [latex]y_3, \, y_4, \, \ldots, \, y_n[/latex].
A time series that exhibits a seasonal component can have a seasonal differencing filter applied. Monthly observations from a time series with an annual seasonal component, for example, can have the seasonal differencing filter
applied to eliminate the seasonal effects. There will be 12 fewer observations in the new time series after applying this filter. If the original time series observations are [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex], then the time series observations that result from applying the filter associated with the ∇12 operator are [latex]y_{13}, \, y_{14}, \, \ldots, \, y_n[/latex].
We now illustrate the application of a differencing filter. The next example applies a single difference filter to the Australian population time series.
So far, two classes of filters have been introduced. The first class is known as a transformation; the second class is known as a detrending filter. Two types of detrending filters were introduced: curve fitting and differencing. We now turn to a third class of filter which is known as a linear filter. Differencing is a special case of a linear filter.
Linear Filters
Linear filters provide a wide array of options for converting the original time series [latex]\left\{ x_t \right\}[/latex] to another time series [latex]\left\{ y_t \right\}[/latex]. The general form of a linear filter is
where the coefficients cs are real-valued constants. It is often the case that [latex]t_0 < 0[/latex] and [latex]t_1 > 0[/latex], which means that the time series [latex]\left\{ y_t \right\}[/latex] is a linear combination of the chronological current, previous, and future values of [latex]\left\{ x_t \right\}[/latex] in time.
One purpose of a linear filter is smoothing the original time series by using what is known as a moving average. When the coefficients sum to one, written symbolically as
this linear filter is a moving average. One elementary example of a symmetric moving average is when [latex]t_0 = - t_1[/latex] with identical weights
In this case, the smoothed time series [latex]\left\{ y_t \right\}[/latex] is the arithmetic mean of
- the current value of the time series [latex]\left\{ x_t \right\}[/latex],
- the t1 previous values of the time series [latex]\left\{ x_t \right\}[/latex],
- the t1 future values of the time series [latex]\left\{ x_t \right\}[/latex],
for a total of [latex]2t_1 + 1[/latex] values averaged. The symmetric moving average [latex]\left\{ y_t \right\}[/latex] will have [latex]2t_1[/latex] fewer observations than the original time series [latex]\left\{ x_t \right\}[/latex] because the average cannot be computed for the first and last t1 observations in [latex]\left\{ x_t \right\}[/latex]. The smoothed values of the first 100 Dow Jones Industrial Average closing values during the year 2000, introduced in Example 7.4, will be illustrated next.
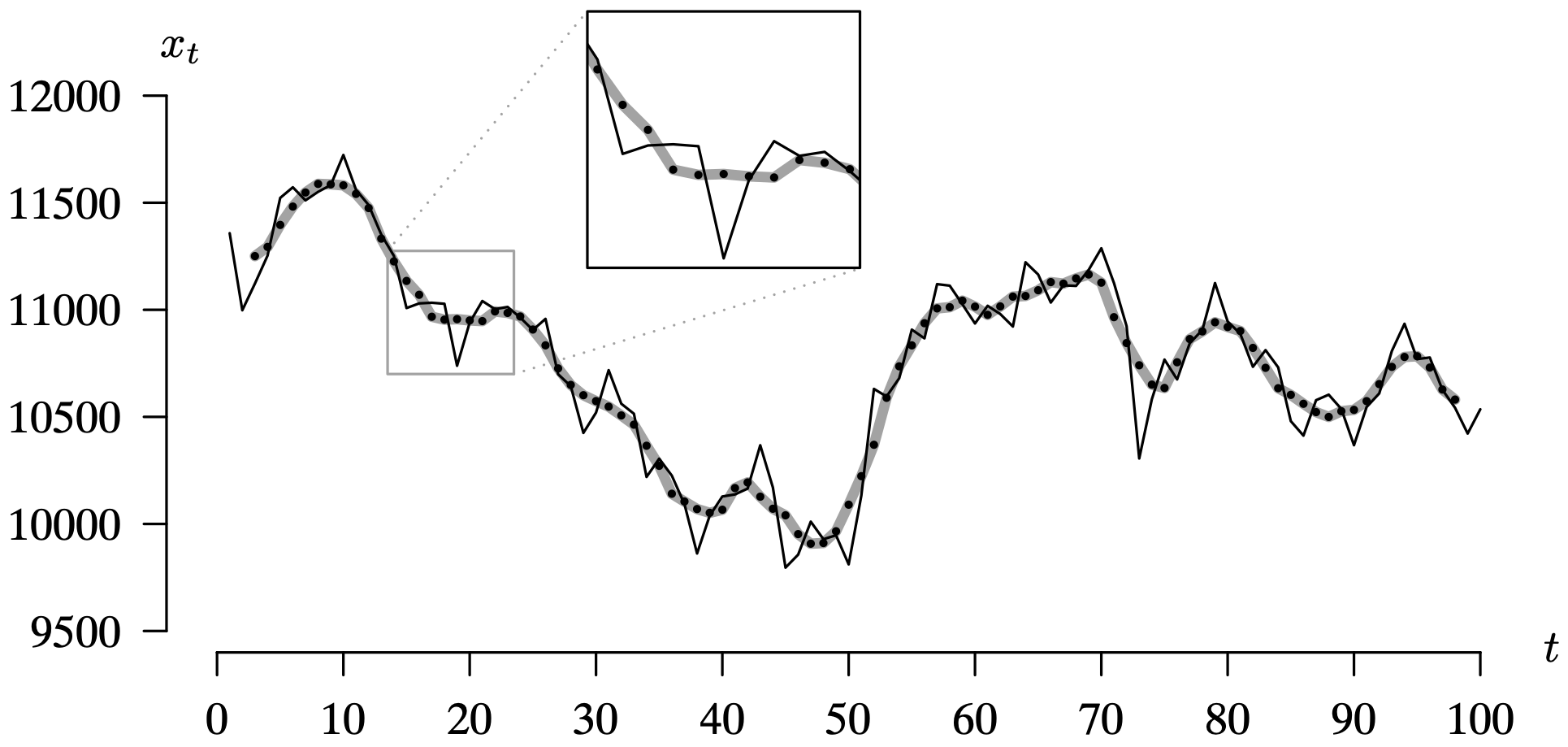
Long Description for Figure 7.25
The horizontal axis t ranges from 0 to 100 in increments of 10 units. The vertical axis x subscript t ranges from 9500 to 12000 in increments of 500 units. The time series plot behaves in a spike pattern. D J I A graph increases from 11000 to 12000 from t equals 0 to 10, progressively decreasing to 9800 at t equals 50 with many vacillations. It then increases to 11300 at t equals 70, and vacillates between 10500 and 11000 from t equals 80 to t equals 100. The five point moving average curve lies along the time series plot, in a similar trend. The trend from t equals 15 to t equals 20 is highlighted where D J I A vacillates between 10700 and 11300 and five point moving average decreases from 11300 to 11000. All data are estimated.
We now illustrate the case in which filters are applied to a time series in a serial fashion as illustrated below.
Let the values in the original time series be
Consider the linear filter which is a three-point moving average (in which [latex]t_1 = 1[/latex])
This linear filter results in the time series [latex]\left\{ y_t \right\}[/latex] consisting of the observations
Now consider applying this same linear filter again, but this time to [latex]\left\{ y_t \right\}[/latex]:
The second linear filter results in the time series [latex]\left\{ z_t \right\}[/latex] consisting of the observations
when written in terms of the original time series [latex]\left\{ x_t \right\}[/latex]. Notice that the serial application of the two linear filters is the same as the application of a single linear filter with the coefficients
The R convolve function calculates the coefficients of the linear filter associated with two linear filters applied to a time series. In the example described here, the coefficients can be determined with the R statements

The application of two linear filters in sequence is illustrated in the next example.

Long Description for Figure 7.26
The horizontal axis t ranges from 0 to 100 in increments of 10 units. The vertical axis x subscript t ranges from 9500 to 12000 in increments of 500 units. The time series plot behaves in a spike pattern. D J I A graph increases from 11300 to 11800 from t equals 0 to 10, progressively decreases to 9800 at t equals 50 with many vacillations. It then increases to 11300 at t equals 70, decreases to 10400 at t equals 72, and vacillates between 10500 and 11000 from t equals 80 to t equals 100. The nine point moving average curve lies along with the time series plot, in a similar trend. The graph decreases from 11500 to 10000 from t equals 0 to 50, increases to 11000 at t equals 70, and decreases to 10800 at t equals 100. All data are estimated.
Some experimentation is often necessary to achieve a moving average that provides the appropriate amount of smoothing. The amount of smoothing desired is problem specific. Another type of symmetric moving average that places the most weight on the current value xt and decreasing weight to more distant observations is to use the terms in the expansion of
as coefficients in a weighted moving average. When [latex]t_1 = 2[/latex], for example, the coefficients are
The numerators can be recognized as one row in Pascal's triangle. The weights must sum to 1 because [latex]1 / 2 + 1 / 2 = 1[/latex].
For a time series without a trend that contains a seasonal component, a special linear filter can be applied. Consider a time series of monthly observations with seasonal variation. A common way to eliminate the seasonal component is the linear filter
This linear filter has 13 coefficients
which places a weight of [latex]1 / 12[/latex] on the current observation xt and each observation within five months of xt and splits the weight between the two months that are six months before and six months after the current observation. Notice that the filtered time series [latex]\left\{ y_t \right\}[/latex] will have 12 fewer observations than the original time series [latex]\left\{ x_t \right\}[/latex] because the moving average loses six points at the beginning of the time series and six points at the end of the time series. This seasonal weighted average will be illustrated in the next example for the monthly home energy consumption time series.
All of the linear filters we have encountered so far have been symmetric moving averages. Each of them has reached as far into the past as they have into the future. One weakness of these filters is that in many settings we often do not have any future observations. So in many practical problems the linear filter
is rewritten to avoid any observations in the future as
for some negative integer index t0. The most well-known of these filters is known as the exponentially-weighted moving average, often abbreviated EWMA, which can be written as
where the weights cs are given by
for [latex]0 < \alpha < 1[/latex] and [latex]s = -\infty , \, \, \ldots, \, -2, \, -1, \, 0[/latex]. The weights in the exponentially-weighted moving average must sum to one because they form a geometric series:
The exponentially-weighted moving average gives weight α to the current observation, and then geometrically declining weights to previous observations. So the parameter α can be thought of as a dial or tuning parameter which controls the amount of smoothing. Large values of α mean very little smoothing; small values of α mean significant smoothing. While it is daunting to think about values of a time series [latex]\left\{ x_t \right\}[/latex] running back in time to [latex]-\infty[/latex], it is possible to avoid the infinite summation. The exponentially-weighted moving average filter can be rewritten as
that is, the exponentially-weighted moving average is α times the current value in the time series xt plus [latex]1 - \alpha[/latex] times the previous value in the moving average. Arbitrarily setting [latex]y_1 = x_1[/latex] to initiate this recursive relationship, the initial terms in the moving average are
Notice that the extreme case of [latex]\alpha = 1[/latex] is possible in this recursive equation, and this corresponds to a moving average that is identical to the original time series: [latex]y_1 = x_1[/latex], [latex]y_2 = x_2[/latex], [latex]y_3 = x_3[/latex], etc. This extreme case corresponds to no smoothing at all.
The next example applies the exponentially-weighted moving average to the first [latex]n = 100[/latex] Dow Jones Industrial Average closing observations during the year 2000.
This concludes the discussion of filters that can be applied to a time series. The three classes of filters that were presented in this section are
- transformations,
- detrending filters, and
- linear filters.
Filters can be applied for several different purposes, including: (a) to stabilize the variance of a time series whose variance increases with time, (b) to stabilize the variance of a time series in which larger values are more variable than smaller values, (c) to make error terms look approximately normally distributed, (d) to express a time series with a seasonal component as an additive model, (e) to detrend a time series containing a trend, (f) to estimate and eliminate a seasonal component in a time series without a trend, and (g) to smooth a time series. Many of these reasons for using a filter on a time series will be discussed subsequently.
The next section uses two filters in series in order to decompose a time series into trend and seasonal components. Decomposition will be applied to the international air travel time series and the home energy consumption time series from the first two examples in this chapter.
7.3.2 Decomposition
The time series plots on the four examples from Section 7.1.1 have revealed certain types of patterns that appear in many time series. The partial list below contains the most common types of variation in time series. One common approach to decomposing a time series into these various types of variation is to remove the detected types of variation one-by-one until only noise (that is, random variation) remains.
- Trend. The time series consisting of the number of international airline passengers between 1949 and 1961 from Example 7.2 had a clear and obvious long-term systemic increase in its mean value as air travel became more popular over that time period. Detecting trends and including them in a time series model is an important part of the analysis of a time series that will be illustrated in the next example.
- Seasonal variation. Both the home energy consumption time series from Example 7.1 and the international airline passenger time series from Example 7.2 exhibit seasonal variation. The period associated with the seasonal variation in both cases was one year. A single time series is capable of having multiple seasonal variation cycles. Outdoor temperature, for example, has both an annual cycle (warmer during the summer and cooler during the winter) and a daily cycle (warmer during the day and cooler during the night). The frequency of the daily cycle is 365 times greater than the frequency of the annual cycle. (To be more careful, the frequency is actually 365.2422 times greater.)
- Other cyclical variation. There are other types of cyclical variation that have an unknown period that might be included in a mathematical model that describes the time series. Economists, for example, often refer to business cycles that might influence the values in a time series. Business cycles typically have a varying and unknown period generally ranging from a few years to decades.
- Remaining variation. Once the trend, seasonal variation, and other cyclical variation have been removed from the original time series, a time series with no trend, seasonal, or cyclic variation is obtained. Once this new time series is obtained, it is common practice to plot these values to see how closely they approximate noise terms. The final step in constructing a time series model for the original process is often fitting a time series model to the residual time series, which reflects the noise terms in the time series model.
We now consider mathematical models for decomposing a time series into these constituent parts. Just as a probability model like the normal or exponential distribution is used to approximate the probability distribution from which a data set is drawn in classical statistics, we want to develop a probability model for the time series [latex]\left\{ X_t \right\}[/latex]. This probability model will be more complicated than the random walk model because we would like it to include both trends and seasonal variation. An additive model to describe [latex]\left\{ X_t \right\}[/latex] is
where the mt term models the trend, the st term models the seasonal variation with fixed period, and the ϵt term models the noise. In an ideal probabilistic modeling sequence, once the trend and seasonality terms have been estimated and removed from the time series, only random variation remains. We have ignored other cyclic variation (for example, business cycles) in this particular mathematical model. Notice that the trend term mt and the seasonal variation term st are set in lowercase because these are assumed to be deterministic functions of t in the model. The stochastic element of the time series model comes from the ϵt term. A multiplicative model to describe [latex]\left\{ X_t \right\}[/latex] is
The multiplicative model is often appropriate in the case in which the variance of the time series increases with time. This is because taking the natural logarithm of both sides of this model yields
which is an additive model for the time series [latex]\left\{ \ln \, X_t \right\}[/latex].
Decomposing a time series into its constituent parts can be preformed in R with the decompose function. The additive model is the default. The next example applies the decompose function to the time series consisting of the international airline passengers.
The international airline passengers data set had its own distinct signature for its seasonal component. The next example plots the analogous seasonal component for the home energy consumption data.
It is important to not treat a function like decompose as a just a black box that decomposes a time series without knowing the internal workings of the function. It is crucial to know exactly what is going on inside of decompose for (a) proper interpretation of the output of the function, and (b) the ability to modify the function. In that light, we now show the intermediate steps that occurred in decompose using the object names in decompose that resulted in the values plotted in Figure 7.31.

Try typing these statements into R and viewing the resulting objects. The bullet points below give a line-by-line explanation of the algorithm associated with this R code.
- The first statement reads the home energy consumption time series into the vector kwh.
- The second statement converts the vector named kwh to a time series named kwh.ts with monthly values beginning in January of 2011 via the ts function.
- The third statement calculates the length of the time series as [latex]l = 96[/latex].
- The fourth statement extracts the frequency of the time series as [latex]f = 12[/latex].
- The fifth statement uses the filter function to apply a 13-point moving average to the original time series, which results in a time series named trend. The extreme values in this moving average are identical months separated by one year, each getting weight [latex]1 / 24[/latex], and the interior 11 months each get weight [latex]1 / 12[/latex]. Notice that the first six and last six values of the resulting time series trend are NA, as expected. The 13-point moving average is first reported in July of 2011, using the 13 values from the original time series from January 2011 to January 2012. Each value in trend is effectively an annual average of energy consumption, so this is a fairly flat time series for the energy consumption time series data because there does not appear to be any significant trend. The values in trend are plotted in Figure 7.27.
- The sixth statement creates a time series named season which is the difference between the original time series kwh.ts and the time series trend. In time series analysis, this step is known as detrending. This new time series season isolates the empirical seasonal component, which will change from one year to the next. The remaining R statements are designed to average these seasonal components.
- The seventh statement calculates the number of periods in the original time series: [latex]l / f = 96 / 12 = 8[/latex].
- The eighth statement creates a vector named index that will be used in the calculation of the seasonal component averages. For the energy consumption data, the eight elements of index are [latex]0, \, 12, \, 24, \, \ldots , \, 84[/latex].
- The ninth statement uses the numeric function to initialize the 12-element vector named figure, which will contain the seasonal component averages.
- The tenth statement contains a for loop which uses the mean function to calculate the seasonal component averages for each of the 12 months.
- The eleventh statement centers these seasonal component averages around zero.
- The twelfth statement uses the ts function to create a time series named seasonal which contains 8 periods of the seasonal component averages with a frequency of [latex]f = 12[/latex] and a start time of January of 2011. These are the values that are plotted in Figure 7.31.
View the decompose function by simply typing
In addition to the R statements described above, you will see (a) error trapping at the top of the function, (b) several conditional statements to account for the additive and the multiplicative models, and (c) code that will adjust to a time series consisting of incomplete periods.
The figures that we have seen so far have plotted a time series [latex]\left\{ x_t \right\}[/latex] or a filter applied to create another time series [latex]\left\{ y_t \right\}[/latex]. The critical initial step of plotting the time series and making a careful examination of the plot should never be skipped.
7.3.3 Computing
Regression can be used to fit a model to a time series using the built-in lm (linear model) function in R. This is illustrated for the AirPassengers time series below.
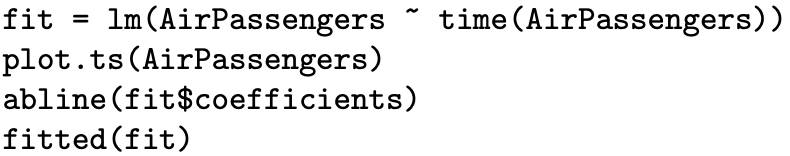
The first statement sets the object fit to a list that contains the results of a simple linear regression of time(AirPassengers) as the independent variable (the predictor) and AirPassengers as the dependent variable (the response). The second statement plots the time series in the usual fashion using the plot.ts function. The third statement appends the plot with the regression line using the abline function. Finally, the fitted values can be extracted by the call to fitted(fit) as shown above or by using fit$fitted.values.
A second way to remove a trend from a time series [latex]x_1, \, x_2, \, \ldots, \, x_n[/latex] is differencing. The difference operator ∇ defined by
(where B is the backshift operator defined by [latex]Bx_t = x_{t - 1}[/latex]) can be used to remove a linear trend. The R function diff can be used to difference a time series. The following statement creates a time series that contains the differences between adjacent values in the AirPassengers time series.

There will be one fewer observation in the differenced time series than in the original time series. A quadratic trend in a time series can be detrended by applying the differencing operator ∇ twice to the original time series:
This detrending filter can be written with the backshift operator as [latex](1 - 2B + B ^ 2) x_t[/latex]. Second-order differences, denoted by [latex]\nabla ^ 2 x_t[/latex], can be calculated by applying the diff function twice:
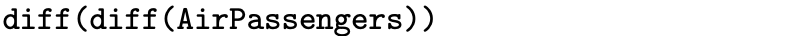
or by using the differences argument in the diff function:
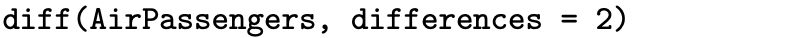
Monthly observations from a time series with an annual seasonal component, for example, can have the seasonal differencing filter
applied to eliminate the seasonal effects. The lag argument is added to the diff function in order to do this type of seasonal differencing.
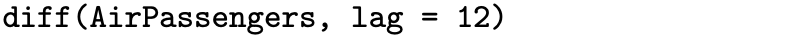
There will be 12 fewer observations in the new time series after applying this filter.
The backshift operator B, which is useful in writing differencing operations compactly, is defined by [latex]B x_t = x_{t - 1}[/latex], or more generally as [latex]B ^ m x_t = x_{t - m}[/latex]. A single application of the B operator can be achieved by a call to the lag function.
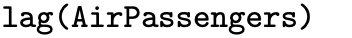
The first observation in the resulting time series is December of 1948. The time series has simply been shifted back in time by one month. To apply the B operator twice, denoted by B2, the second argument should be set to 2.

The first observation in the resulting time series is November of 1948. In order to shift a time series forward in time, a negative value for the second argument is used.
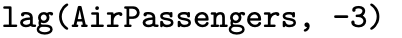
The first observation in the resulting time series is April of 1949.
The intersection of several time series can be achieved with the ts.intersect function, which is illustrated below.

The elements of the resulting intersection of the three time series will only be defined on common time values. A related function named ts.union, will take the union of the constituent time series, appending an NA to positions in any of the constituent time series without observations.
Occasions arise in which only a subset of a time series is of interest. The window function shown below extracts the portion of the AirPassengers time series between January of 1951 and June of 1957.
A linear filter can also be applied to a time series using the filter function. The example below calculates a 12-point moving average of the AirPassengers time series.
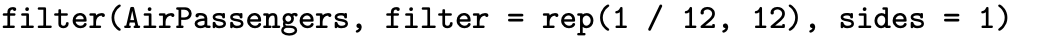
A time series can be decomposed into trend, seasonal, and random components using the decompose function.
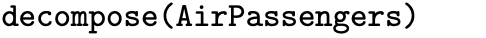
These components can be viewed by embedding this command into the plot function.
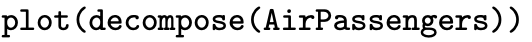
This provides only a graph of the four components. The decompose function provides a rather elementary way of decomposing time series. A more sophisticated approach using the loess (locally estimated scatterplot smoothing) method is the stl (which is an abbreviation for seasonal decomposition of a time series by loess) function.
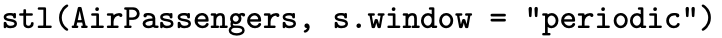
7.4 Exercises
-
7.1 White noise (WN), iid noise (IID), and Gaussian white noise (GWN) were introduced in Definition 7.1. The three classes are related by
Indicate the strongest class of noise associated with the following three time series.
- [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are mutually independent and identically distributed [latex]N(0, \, 1)[/latex] random variables.
- [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are mutually independent random variables with [latex]X_t \sim N(0, \, 1)[/latex] when t is even and [latex]X_t \sim U \left( - \sqrt{3}, \sqrt{3} \, \right)[/latex] when t is odd.
- [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] are mutually independent and identically distributed [latex]U(-2, \, 2)[/latex] random variables.
-
7.2 Let [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] be n observations from the random walk model described in Example 7.4. Find [latex]V \big[ \bar X \big][/latex], where [latex]\bar X[/latex] is the sample mean.
-
7.3 The realization of the random walk in Example 7.4 was generated by using a while loop in R. Write R code to generate the same time series values without using a loop.
-
7.4 The time series of the number of monthly accidental deaths in the United States from 1973 to 1978 is given in USAccDeaths in R. Make a plot of the time series values and comment on any features you can glean from the plot.
-
7.5 Classify each of the following stochastic processes by time (discrete or continuous) and state (discrete or continuous).
- The number of eastbound cars stopped at a particular stoplight over time.
- The location of a taxi cab (classified as city, airport, or suburbs) at the end of each passenger's ride.
- The temperature of a puppy measured at 20-minute intervals.
- A person's internal body temperature over time.
- The number of goldfish on inventory at a local pet shop.
-
7.6 Consider the random variables [latex]X_1, \, X_2, \, \ldots, \, X_n[/latex] and [latex]Y_1, \, Y_2, \, \ldots, \, Y_m[/latex] with associated finite population means, population variances, and population covariances. Show that
for real-valued constants [latex]a_1, \, a_2, \, \ldots, \, a_n[/latex] and [latex]b_1, \, b_2, \, \ldots, \, b_m[/latex].
-
7.7 The time series [latex]\left\{ X_t \right\}[/latex] consists of the number of spots on the up face of sequential rolls of a fair die.
- Is this time series strictly stationary?
- What is the population mean function?
- What is the population autocovariance function?
- What is the population autocorrelation function?
-
7.8 Consider the (tiny) time series X1, X2, X3, whose values are the cumulative number of spots showing in three rolls of a fair die. More specifically, if R1, R2, and R3 denote the outcomes of the three rolls, then [latex]X_1 = R_1[/latex], [latex]X_2 = R_1 + R_2[/latex], and [latex]X_3 = R_1 + R_2 + R_3[/latex].
- What is the population mean function?
- Is this time series strictly stationary?
- Is this time series stationary?
- What is the population variance–covariance matrix of X1, X2, X3?
- Perform a Monte Carlo simulation which provides convincing numerical evidence that the population variance–covariance matrix from part (d) is correct.
-
7.9 Argue whether the time series of monthly home energy consumption observations from Example 7.1 is a stationary time series.
-
7.10 Consider the time series [latex]\left\{ X_t \right\}[/latex] consisting of white noise terms defined by
- Is this time series strictly stationary?
- Is this time series stationary?
-
7.11 The energy consumption time series introduced in Example 7.1 was given in number of kilowatt hours per month. The varying number of days per month was not taken into account in the analysis performed on this data set in this chapter. Adjust the time series so that the varying month length has been taken into account and answer the following.
- The original time series had the maximum monthly energy consumption in January of 2018. Which month has the maximum monthly energy consumption in the adjusted time series?
- Make a plot of the time series using the units average daily number of kilowatt hours.
- Use the R acf function to calculate the sample autocorrelation at lag 3. Interpret the sign of the sample lag 3 autocorrelation.
-
7.12 The R built-in data set nhtemp contains the average annual temperatures in New Hampshire from 1912 to 1971. Plot the time series and correlogram.
-
7.13 Consider a time series of [latex]n = 100[/latex] observations which are Gaussian white noise with [latex]\sigma_Z = 1[/latex]. Use Monte Carlo simulation to estimate the probability that the lag 3 sample autocorrelation falls between [latex]-z_{\alpha / 2} / \sqrt{100}[/latex] and [latex]z_{\alpha / 2} / \sqrt{100}[/latex], where [latex]\alpha = 0.05[/latex]. Report your estimate to 3-digit accuracy.
-
7.14 The sojourn time of a customer in a single-server queue is defined as the waiting time plus the service time. Consider 100 consecutive sojourn times for customers in a single-server queue with exponential times between arrivals with population mean 1 and exponential service times with population mean 0.9. (This is a special case of what is known in queueing theory as an M/M/1 queue. The first M is for Markov, and indicates that the times between arrivals is exponentially distributed. The second M is also for Markov, and indicates that the service times are exponentially distributed. The 1 indicates that there is a single server.) Also assume that the first 1000 customer sojourn times have been discarded so that the system has “warmed up.” A realization of these 100 consecutive sojourn times can be generated in R and placed into the vector x with the statements

- Write a paragraph that outlines whether or not the stationarity assumption is appropriate in this setting.
- Before running a simulation, predict whether the sample lag 3 autocorrelation will be positive, zero, or negative.
- Make three runs of this simulation with three different seeds and plot the three sample autocorrelation functions on the same set of axes (plot them as points connected by lines rather than spikes) for the first 20 lags.
-
7.15 Consider a stationary time series [latex]\left\{ X_t \right\}[/latex]. For [latex]k = 1, \, 2, \ldots[/latex], the lag k population partial autocorrelation [latex]\rho ^ * (k)[/latex] can be written as the last component of the vector defined by
where [latex]\Gamma_k[/latex] is the [latex]k \times k[/latex] variance–covariance matrix of any k elements of the time series and [latex]\gamma_k = \big( \gamma(1), \, \gamma(2), \, \ldots , \, \gamma(k) \big) ^ \prime[/latex]. Show that this way of calculating the lag k population partial autocorrelation is equivalent to that given in Definition 7.8 for [latex]k = 1[/latex] and [latex]k = 2[/latex].
-
7.16 Consider a three-point moving average.
- What are the coefficients associated with three of these moving averages applied in series.
- Check your solution using the R convolve function.
- Apply this series of three filters to the AirPassengers data set and plot the smoothed series.
-
7.17 The logarithm and square root transformations are commonly used on a time series whose variability increases with time. Propose a transformation for a time series whose variability decreases with time.
-
7.18 Find the population autocorrelation function for an m-point moving average of a white noise time series, where m is an odd, positive integer.
-
7.19 The R decompose function can be used to decompose a time series. Another R function named stl is a more sophisticated function for decomposing a time series. Apply this function to the built-in R time series JohnsonJohnson, which contains the quarterly earnings, in dollars, for one share of stock in Johnson & Johnson from 1960 to 1980. Plot the trend and seasonal components of the decomposed time series. Which quarter tends to have the highest quarterly earnings? Considering the seasonal part of the decomposed model, what is the difference between the best and worst quarter's earnings to the nearest penny?

