Research Supplement: Correlational Designs
Irene Feng
NON-Experimental Designs
While every study psychologists do can inform us about how people act, behave, or think, not every study can make the same types of claims. This goes back to the study design itself. The way psychologists design different studies means we can draw different conclusions.
Although experimental designs are the most reliable and powerful method for determining cause and effect, it is not always possible to manipulate variables in psychology (or other sciences, for that matter). For example, one cannot “make” someone male or female, or a particular age, etc. We can only select subjects already possessing the different attributes. We do not have the power to manipulate geographic or climatic variables to see the extent to which they influence behavior. Many variables cannot be manipulated for ethical reasons. For example, we cannot systematically punish children severely to see if that is an effective technique for eliminating undesirable behavior. Indeed, some have even questioned studying the effect of punishment on the dangerously self-destructive acts of autistic children (Bettelheim, 1985). For these reasons, many in the other laboratory sciences describe psychology as “soft.” Sometimes they even question the possibility of conducting psychology as a science. The research findings described in this book attest to the fruitfulness of applying the scientific method to psychological questions. The discipline of psychology frequently applies non-experimental designs under conditions where experimental procedures are logistically impossible, prohibitive in cost, or unethical.
Correlational Design
With correlational studies, we can examine the relationship between two variables. We only observe what is happening, we don’t change anything. For example, a study that looked at the relationship between education level and income would be correlational. We cannot attribute a causal effect because we do not manipulate either of these variables.! In a correlational study, we only measure variables, not the effects of variables on other variables. We might be able to say that higher education is related to higher income, and we can say how strong that relationship is, but we cannot say that one causes the other. There is no way to randomly assign people to education levels and design an experiment. A quasi-experiment is only possible with advanced statistics, because we could not control any conditions around geographic location, job, family, quality of education, mental health, and so much more that could be involved in the relationship between education and income. Because there are so many variables unaccounted for, they could potentially influence our results and could be the reason why we see the relationship.
In correlational research, scientists do not intervene and measure changes in behavior. Instead, they passively observe and measure variables and identify patterns of relationships between them. For example, the graph below show’s a study on donations and happiness (Dunn et all 2008). Dr. Dunn’s team asked participants how much of their income they donated to charity in the past month; she later asked them how happy they were (using a 5-point scale). Then they looked at the relationship between the two variables. Dunn found that the more donations people made to charity; the happier they reported feeling.
How do we “look at the relationship between two variables?” This is a statistic called a correlation coefficient – it tells us about how strong the relationship and which direction it goes in. First, we create a scatterplot (see Figure 4.6). In the scatterplot, each dot represents a person in the study and their happiness level and donation amount. We call this a data point.
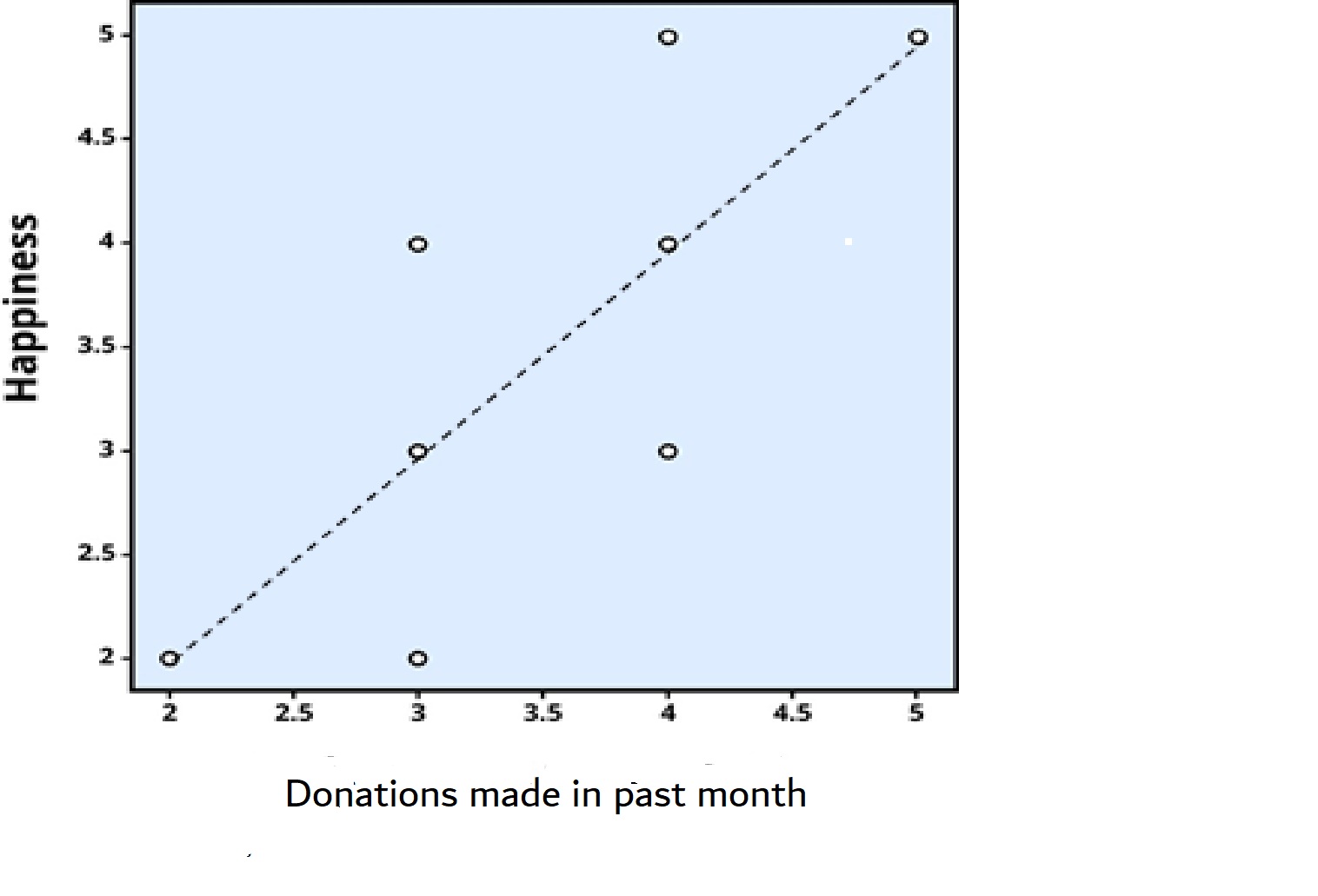
We have added a best fit (dotted) line through the data in Figure 4.6, the line represents the average relationship between the two variables. It has equal numbers of points above and below it. The correlation coefficient (abbreviated as r) is calculated from the data points. The sign of r (positive or negative) indicates the direction of correlation. In Figure 4.6, the line slopes upwards, therefore, r is a positive number (+0.81) indicating that the data show a positive correlation. In other words, the variables move in the same direction – as one goes up so does the other. Low donations correlate with low happiness, and high donations with high happiness ratings.
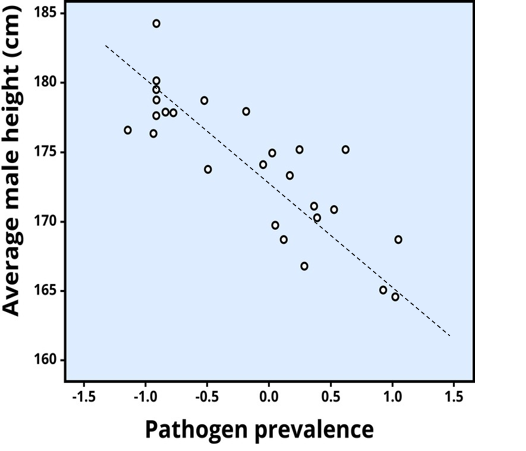
Figure 4.7 shows the data from a different research study. We see the relationship between average height of men in different countries on the y-axis and the prevalence of a pathogen (something that causes disease) in each country on the x-axis. Each dot represents a different country. The line of best fit slopes downwards because there is a negative correlation between the two variables. We can see that countries with taller men have lower incidence of the pathogen and vice versa. In other words, as one variable (height) goes up, the other one (pathogen prevalence) goes down. In Figure 4.7, the correlation coefficient (r = -0.83) is a negative number.
The strength of a correlation tells us about the closeness of the relationship between the two variables. If all the points sat on the best fit lines, this would be the very strong relationship and r would be 1 or -1 (depending on the direction of the association). The higher the absolute value of r (ignore the +/- sign), the stronger the relationship. Perhaps you can see that the dots are a little closer to the line in Figure 4.7 compared to Figure 4.6? This is because the absolute value of r is slightly larger ( a stronger correlation) for Figure 4.7 (-0.83) compared to Figure 4.6 (+0.81). The relationship between variables can vary from strong to weak. Sometimes, r is so low (close to zero), that we say there is no correlation, or the variables are uncorrelated, and the best fit line would be horizontal or flat.
Correlation is NOT causation
Correlational studies like the ones we see in Figures 4.6 and 4.7are very useful for making predictions about the relationships between two variables. They are usually cheaper and less time-consuming to run than experiments and often serve as a start to a more rigorous design that can investigate the causes.
Frequently non-experimental studies can provide information about the relationship between variables despite not being able to demonstrate cause and effect. However, even when relationships between variables are compelling, for example when a substantial statistical correlation exists, it is still not possible to conclude cause and effect. Often there is a hidden third variable (or more) underlying the correlation. For example, it is likely there is a high correlation between the number of books in one’s home and success in school. That does not mean that by simply providing books to an individual it will improve school performance. It is likely the number of books in one’s home is indicative of a number of economic and attitudinal advantages. Still, the fact that this correlation exists is informative and could lead to an experiment to test whether there is a cause and effect relationship between the number of books and school performance.
Summary:
Although we cannot say anything definitive about WHY the relationship exists, correlational studies still can be useful for understanding the strength and direction of the relationship between two constructs of interest. We can claim that two variables are related, or correlated, and the correlation coefficient (r) gives us information about how strong the relationship is and in which direction (i.e. whether the variables increase and decrease together, or whether as one increases, the other decreases in value. )

