In tonal music, because intervals are dependent upon the pitches that create them, the consonance and dissonance of intervals is determined by tonality itself. Imagine the interval created by G and B♭, a minor third. In the context of G minor, this is a consonant interval. Respelled as G and A♯, perhaps in the context of B minor, it creates a dissonant augmented second. From a tonal perspective, then, the two intervals are different even though they are the same in isolation (Example 1).

Example 1. Even though B♭ and A♯ are the same key on the keyboard, the intervals of a minor third and an augmented second are distinct in tonal theory.

Contrast this with atonal music. Because atonal music has no tonality, the distinction between B♭ and A♯ no longer matters. In this context, the intervals G–B♭ and G–A♯ are the same. For this reason, we will not use tonal interval names like “minor third.” Instead, we will measure the intervals by the number of semitones between the pitches or pitch classes.

We can describe intervals according to two types of information: pitches vs. pitch classes, and ordered vs. unordered intervals. Combined, this makes four types of intervals, summarized in Example 2. Each of these interval types is explained below.

[table id=18 /]

Example 2. Four interval types in atonal theory.

Pitch Intervals (ordered and unordered)

Pitch intervals are the distance between pitches as measured in half steps, which is to say that octave is taken into consideration. Thus, the interval C₄–E₄ is 4: four half steps are between these notes. But if that E is moved up an octave (C₄–E₅), the interval becomes 16: four half steps between C and E, plus an octave (twelve half steps) between the lower E and the higher E.

Within pitch intervals, there are ordered and unordered variants. To create an ordered pitch interval, simply add a plus or minus sign to indicate whether the interval is ascending or descending. Unordered pitch intervals, by contrast, do not indicate which direction the pitches move in—they are thus more suitable for harmonic intervals. The differences between ordered and unordered pitch intervals are summarized in Example 3.

Ordered Pitch-Class Intervals

Pitch-class intervals are the distance between pitch classes as measured in semitones in pitch class space—that is, around the clock face. Returning to our C₄–E₅ interval, we are now interested just in the pitch classes C and E, without reference to a specific octave

Ordered pitch-class intervals measure the distance between pitch classes, always ascending. This is visualized most easily by picturing the twelve tones around a clock face, then measuring the interval by going around the circle clockwise. Thus, from C to E = 4, but E to C = 8 (Example 4).

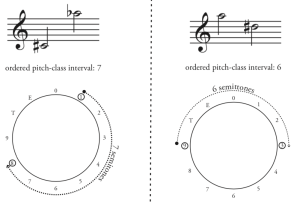
Interval Classes (IC)

Unordered pitch-class intervals are usually called interval classes. Interval class is the smallest possible distance between two pitch classes. On the clock face, this means traveling either clockwise or counter-clockwise, whichever is shortest. Interval class is a useful concept because it relates intervals, their inversions, and any compound versions of those intervals. You should be able to connect this concept to the concept of pitch vs. pitch class: a pitch class is a pitch, its enharmonic respelling(s), and any octave displacements of those spellings.

This means that there are only six interval classes: 1, 2, 3, 4, 5, and 6. If you reach the pitch class interval of 7, it becomes shorter to move counter-clockwise, and 7 becomes 5. For the same reason, 8 becomes 4, 9 becomes 3, and so on. Both C–E and E–C are interval class 4 (Example 5).

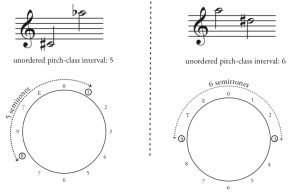
Summary

Using various combinations of pitch interval, pitch-class interval, ordered, and unordered, we arrive at four different conceptions of interval.To wrap your mind around each of these and begin to understand their various analytical uses, think of them on a sliding scale of most concrete (the ordered pitch interval) to most abstract (the unordered pitch-class interval). You can find this related to other concepts in the Set Theory Quick Reference Sheet.

In tonal music, it’s useful to distinguish between a thirteenth and a sixth in some situations, but not others. In the same way, as you analyze atonal music, you will find that different types of intervals are useful for describing different types of phenomena.

• Blank clock faces (integer notation)
• Blank clock faces (letter names)
• Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.

1. Intervals (.pdf, .docx). Asks students to identify interval types (integer notation) within pieces of music. Worksheet playlist