1 Measurements

The Nature of Science

Science is an overarching category of many different disciplines that involve hypothesizing, observation, testing and evidence. It is an ever-changing and fluid field because regardless of the results of research or experimentation, there will always be more questions to ask. Some examples of scientific fields are Biology, Botany, Psychology, Chemistry, Astronomy and Physics.

Introduction to Measurements

Measurements provide much of the information that informs the hypotheses, theories, and laws describing the behavior of matter and energy in both the macroscopic and microscopic domains of chemistry. Every measurement provides three kinds of information: the size or magnitude of the measurement (a number), a standard of comparison for the measurement (a unit), and an indication of the uncertainty of the measurement. While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.

The number in the measurement can be represented in different ways, including decimal form and scientific notation. (Scientific notation is also known as exponential notation; a review of this topic can be found through this link here: Exponential notation review and examples.) For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as 2.98 x 10⁵ kg. The mass of the average mosquito is about 0.0000025 kilograms, which can be written as 2.5 x 10⁻⁶ kg.

Units, such as liters, pounds, and centimeters, are standards of comparison for measurements. A 2-liter bottle of a soft drink contains a volume of beverage that is twice that of the accepted volume of 1 liter. The meat used to prepare a 0.25-pound hamburger weighs one-fourth as much as the accepted weight of 1 pound. Without units a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire: 100 mg given three times per day can be effective as an anticonvulsant, but a single dose of 100 g is more than 10 times the lethal amount.

The measurement units for seven fundamental properties (“base units”) are listed in Table 1.1. The standards for these units are fixed by international agreement, and they are called the International System of Units or SI Units (from the French, Le Système International d’Unités). SI units have been used by the United States National Institute of Standards and Technology (NIST) since 1964. Units for other properties may be derived from these seven base units.

Table 1.1

Everyday measurement units are often defined as fractions or multiples of other units. Milk is commonly packaged in containers of 1 gallon (4 quarts), 1 quart (0.25 gallon), and one pint (0.5 quart). This same approach is used with SI units, but these fractions or multiples are always powers of 10. Fractional or multiple SI units are named using a prefix and the name of the base unit. For example, a length of 1000 meters is also called a kilometer because the prefix kilo means “one thousand,” which in scientific notation is 10³ (1 kilometer = 1000 m = 10³ m). The prefixes used and the powers to which 10 are raised are listed in Table 1.2.

Table 1.2

LINK TO LEARNING: Need a refresher or more practice with scientific notation? Visit this site to go over the basics of scientific notation: Math Skills Review Scientific Notation.

SI Base Units

The initial units of the metric system, which eventually evolved into the SI system, were established in France during the French Revolution. The original standards for the meter and the kilogram were adopted there in 1799 and eventually by other countries. SI stands for Système International, which means international system in French. This section introduces four of the SI base units commonly used in chemistry. Other SI units will be introduced in subsequent chapters.

Length

The standard unit of length in both the SI and original metric systems is the meter (m). A meter was originally specified as 1/10,000,000 of the distance from the North Pole to the equator. It is now defined as the distance light in a vacuum travels in 1/299,792,458 of a second. A meter is about 3 inches longer than a yard (Figure 1.1); one meter is about 39.37 inches or 1.094 yards. Longer distances are often reported in kilometers (1 km = 1000 m = 10³ m), whereas shorter distances can be reported in centimeters (1 cm = 0.01 m = 10⁻² m) or millimeters (1 mm = 0.001 m = 10⁻³ m).

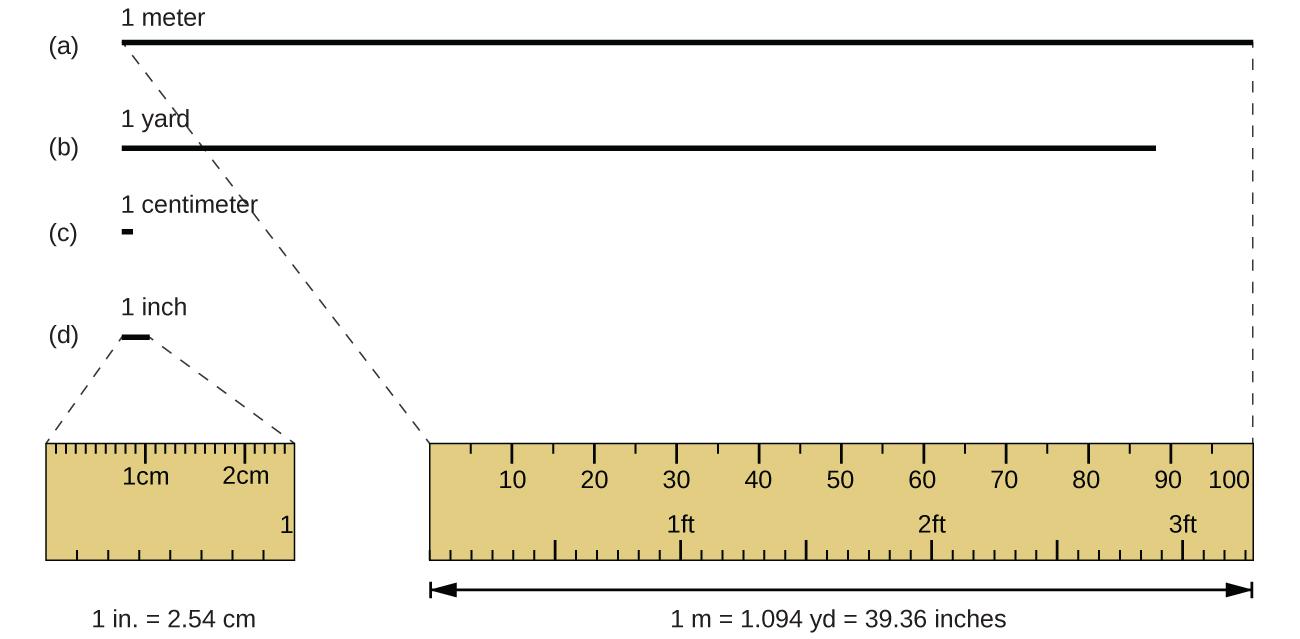
Figure 1.1 The relative lengths of 1 m, 1 yd, 1 cm, and 1 in. are shown (not actual size), as well as comparisons of 2.54 cm and 1 in., and of 1 m and 1.094 yd.

Mass

The standard unit of mass in the SI system is the kilogram (kg). The kilogram was previously defined by the International Union of Pure and Applied Chemistry (IUPAC) as the mass of a specific reference object. This object was originally one liter of pure water, and more recently it was a metal cylinder made from a platinum-iridium alloy with a height and diameter of 39 mm (Figure 1.2). In May 2019, this definition was changed to one that is based instead on precisely measured values of several fundamental physical constants. One kilogram is about 2.2 pounds. The gram (g) is exactly equal to 1/1000 of the mass of the kilogram (10⁻³ kg).

 

Figure 1.2 This replica prototype kilogram as previously defined is housed at the National Institute of Standards and Technology (NIST) in Maryland. (credit: National Institutes of Standards and Technology)

Temperature

The SI unit of temperature is the kelvin (K). The IUPAC convention is to use kelvin (all lowercase) for the word, K (uppercase) for the unit symbol, and neither the word “degree” nor the degree symbol (°). The degree Celsius (°C) is also allowed in the SI system, with both the word “degree” and the degree symbol used for Celsius measurements. Celsius degrees are the same magnitude as those of kelvin, but the two scales place their zeros in different places (Figure 1.3). Water freezes at 273.15 K (0 °C) and boils at 373.15 K (100 °C) by definition, and normal human body temperature is approximately 310 K (37 °C). Kelvin is used by scientists to better reflect the amount of thermal energy in any measurement, with the absence of energy being 0 K (-273.15 °C), also known as absolute zero. The conversion between these two units and the Fahrenheit scale will be discussed later in this chapter.

              

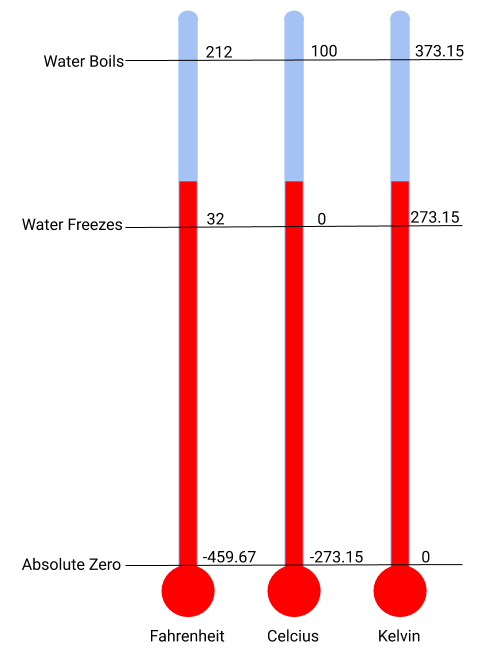
Figure 1.3 An illustration of the different temperature units with their respective benchmarks of where water boils and freezes as well as absolute zero.

Time

The SI base unit of time is the second (s). Small and large time intervals can be expressed with the appropriate prefixes; for example, 3 microseconds = 0.000003 s = 3 x 10⁻⁶ and 5 megaseconds = 5,000,000 s = 5 x 10⁶ s. Alternatively, hours, days, and years can be used.

Derived SI Units

We can derive many units from the seven SI base units. For example, we can multiply the base unit of length (m) by itself three times to define a unit of volume, m^3. We can also use the base units of mass (kg) and length (m) to define a unit of density, which is mass over volume or kg/m^3.

Volume

Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length (Figure 1.4). The standard volume is a cubic meter (m³), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.

A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm³). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts.

A cubic centimeter (cm³) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is equivalent to a milliliter (mL) and is 1/1000 of a liter.

 

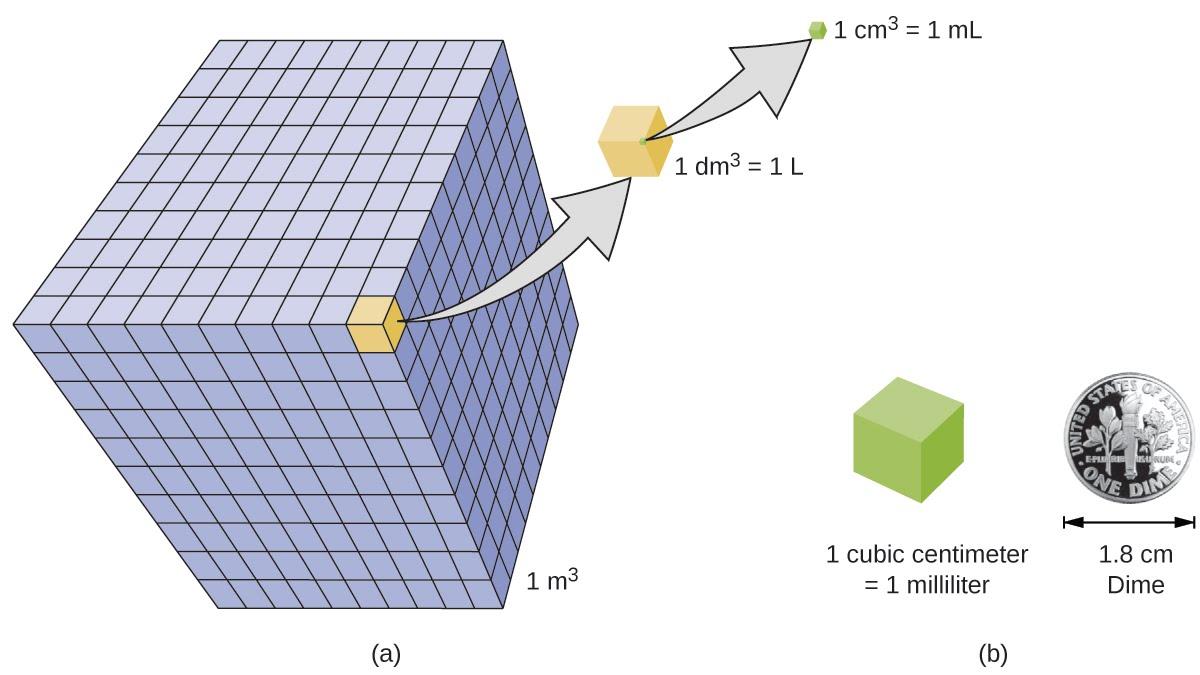
Figure 1.4 (a) The relative volumes are shown for cubes of 1 m³, 1 dm³ (1 L), and 1 cm³ (1 mL) (not to scale). (b) The diameter of a dime is compared relative to the edge length of a 1-cm³ (1-mL) cube.

Density

We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length.

The density of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m³). For many situations, however, this is an inconvenient unit, and we often use grams per cubic centimeter (g/cm³) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm³ (the density of gasoline) to 19 g/cm³ (the density of gold). The density of air is about 1.2 g/L. Table 1.3 shows the densities of some common substances.

Table 1.3

While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements.

density = mass/volume

Check Your Learning

(a) To three decimal places, what is the volume of a cube (cm³) with an edge length of 0.843 cm?

(b) If the cube in part (a) is copper and has a mass of 5.34 g, what is the density of copper to two decimal places?

ANSWER: (a) 0.599 cm³; (b) 8.91 g/cm³

Accuracy and Precision

Scientists typically make repeated measurements of a quantity to ensure the quality of their findings and to evaluate both the precision and the accuracy of their results. Measurements are said to be precise if they yield very similar results when repeated in the same manner. A measurement is considered accurate if it yields a result that is very close to the true or accepted value. Precise values agree with each other; accurate values agree with a true value. These characterizations can be extended to other contexts, such as the results of an archery competition (Figure 1.5).

 

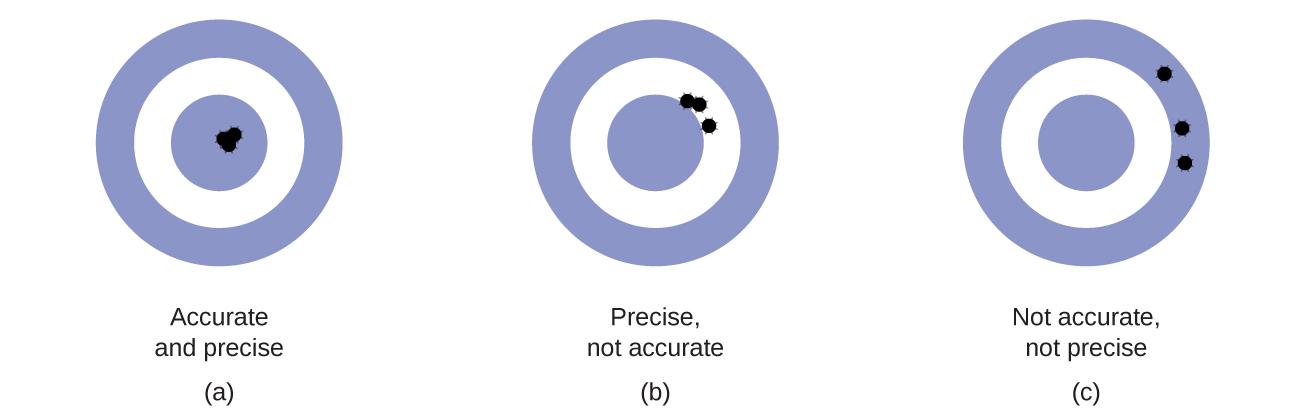
Figure 1.5(a) These arrows are close to both the bull’s eye and one another, so they are both accurate and precise. (b) These arrows are close to one another but not on target, so they are precise but not accurate. (c) These arrows are neither on target nor close to one another, so they are neither accurate nor precise.

Unit Conversion

It is often the case that a quantity of interest may not be easy (or even possible) to measure directly but instead must be calculated from other directly measured properties and appropriate mathematical relationships. For example, consider measuring the average speed of an athlete running sprints. This is typically accomplished by measuring the time required for the athlete to run from the starting line to the finish line, and the distance between these two lines, and then computing speed from the equation that relates these three properties: speed=distance/time

An Olympic-quality sprinter can run 100 m in approximately 10 s, corresponding to an average speed of 100 m/10 s=10 m/s

Note that this simple arithmetic involves dividing the numbers of each measured quantity to yield the number of the computed quantity (100/10 = 10) and also dividing the units of each measured quantity to yield the unit of the computed quantity (meter divided by second = meter per second). Now, consider using this same relation to predict the time required for a person running at this speed to travel a distance of 25 m. The same relation among the three properties is used, but in this case, the two quantities provided are a speed (10 m/s) and a distance (25 m). To yield the sought property, time, the equation must be rearranged appropriately: time=distance/speed

The time can then be computed as: 25 m/(10 m/s) = 2.5 s

Again, arithmetic on the numbers (25/10 = 2.5) was accompanied by the same arithmetic on the units (m/(m/s) = s) to yield the number and unit of the result, 2.5 s. Note that, just as for numbers, when a unit is divided by an identical unit (in this case, m/m), the result is “1”—or, as commonly phrased, the units “cancel.”

These calculations are examples of a versatile mathematical approach known as dimensional analysis (or the factor-label method). Dimensional analysis is based on this premise: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities.

Conversion Factors and Dimensional Analysis

A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor. For example, the lengths of 2.54 cm and 1 in. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio 2.54 cm/1 in. , (2.54 cm=1 in.), or 2.54cm/in.

Several other commonly used conversion factors are given in Table 1.4.

Table 1.4

When a quantity (such as distance in inches) is multiplied by an appropriate unit conversion factor, the quantity is converted to an equivalent value with different units (such as distance in centimeters). For example, a basketball player’s vertical jump of 34 inches can be converted to centimeters by:

34in. × (2.54 cm/1in.) = 86 cm

Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. The numbers of these two quantities are multiplied to yield the number of the product quantity, 86, whereas the units are multiplied to yield in.×(cm/in.) Just as for numbers, a ratio of identical units is also numerically equal to one, in./in.=1, and the unit product thus simplifies to cm. (When identical units divide to yield a factor of 1, they are said to “cancel.”) Dimensional analysis may be used to confirm the proper application of unit conversion factors as demonstrated in the following example.

LINK TO LEARNING: Need a refresher or more practice with dimensional analysis? Visit this site to go over the basics of dimensional analysis: Math Skills Review Dimensional Analysis.

EXAMPLE 1.2

Using a Unit Conversion Factor the mass of a competition frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 g.

Solution: Given the conversion factor, the mass in ounces may be derived using an equation similar to the one used for converting length from inches to centimeters.

x oz=125 g×unit conversion factor

The unit conversion factor may be represented as: 1 oz/28.349 g and 28.349 g/1 oz

The correct unit conversion factor is the ratio that cancels the units of grams and leaves ounces.

x oz=125g× (1 oz/28.349g) = 125/28.349oz = 4.41 oz

Check Your Learning: Convert a volume of 9.345 qt to liters with conversion factor 1 L = 1.05669 qt.

ANSWER: 8.844 L

Beyond simple unit conversions, the factor-label method can be used to solve more complex problems involving computations. Regardless of the details, the basic approach is the same—all the factors involved in the calculation must be appropriately oriented to ensure that their labels (units) will appropriately cancel and/or combine to yield the desired unit in the result. As your study of chemistry continues, you will encounter many opportunities to apply this approach.

EXAMPLE 1.3

While being driven from Philadelphia to Atlanta, a distance of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 L of gasoline.

(a) What (average) fuel economy, in miles per gallon, did the Roadster get during this trip?

(b) If gasoline costs $3.80 per gallon, what was the fuel cost for this trip?

Solution

(a) First convert distance from kilometers to miles:

1250km× (0.62137 mi/1km) = 777 mi

and then convert volume from liters to gallons:

213L× (1.0567qt/1L) × (1 gal/4qt) = 56.3 gal

Finally,

(average) mileage = 777 mi/56.3 gal = 13.8 miles/gallon = 13.8 mpg

Alternatively, the calculation could be set up in a way that uses all the conversion factors sequentially, as follows:

(1250km/213L) × (0.62137 mi/1km) × (1L/1.0567qt) × (4qt/1 gal) = 13.8 mpg

(b) Using the previously calculated volume in gallons, we find:

56.3gal × ($3.80/1gal) = $214

Check Your Learning: A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km (two significant digits).

(a) What (average) fuel economy, in miles per gallon, did the Prius get during this trip?

(b) If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?

ANSWER: (a) 51 mpg; (b) $62