6 Physics! Conservation of Mechanical Energy
Energy plays an essential role both in everyday events and in scientific phenomena. You can no doubt name many forms of energy, from that provided by our foods, to the energy we use to run our cars, to the sunlight that warms us on the beach. You can also cite examples of what people call energy that may not be scientific, such as someone having an energetic personality. Energy not only has many interesting forms; it is involved in almost all phenomena and is one of the most important concepts of physics. What makes it even more important is that the total amount of energy in the universe is constant. Energy can change forms, but it cannot appear from nothing or disappear without a trace. Energy is thus one of a handful of physical quantities that we say is conserved.

Conservation of energy (as physicists like to call the principle that energy can neither be created nor destroyed) is based on experiment. Even as scientists discovered new forms of energy, conservation of energy has always been found to apply. Perhaps the most dramatic example of this was supplied by Einstein when he suggested that mass is equivalent to energy (his famous equation E=mc2).
From a societal viewpoint, energy is one of the major building blocks of modern civilization. Energy resources are key limiting factors to economic growth. The world use of energy resources, especially oil, continues to grow, with ominous consequences economically, socially, politically, and environmentally.
There is no simple, yet accurate, scientific definition for energy. Energy is characterized by its many forms and the fact that it is conserved. We can loosely define energy as the ability to do work, admitting that in some circumstances not all energy is available to do work. Work is intimately related to energy and how energy moves from one system to another or changes form.
EXAMPLE 6.1 CALCULATING THE KINETIC ENERGY OF A PACKAGE
Suppose a 30.0-kg package on a roller belt conveyor system is moving at 0.500 m/s. What is its kinetic energy?
Strategy
Because the mass (m) and speed or velocity (v) are given, the kinetic energy can be calculated from its definition as given in the equation KE = (1/2) mv2.
Solution
The kinetic energy is given by KE = (1/2) mv2. Entering known values gives
KE = 0.5 * (30.0kg)*(0.500m/s)2
which yields
KE=3.75kg⋅m2/s2=3.75 J.
Discussion
Note that the unit of kinetic energy is the joule (kg⋅m2/s2). It is interesting that, although this is a fairly massive package, its kinetic energy is not large at this relatively low speed. This fact is consistent with the observation that people can move packages like this without exhausting themselves.
In Figure 6.2, if the object is lifted straight up we refer to the energy the object has due to gravity as potential energy (PE) gained by the object, recognizing that this is energy stored in the gravitational field of Earth. Why do we use the word “system”? Potential energy is a property of a system rather than of a single object—due to its physical position. An object’s gravitational potential energy is due to its position relative to the surroundings within the Earth-object system. The force applied to the object is an external force, from outside the system. When it does positive work it increases the gravitational potential energy of the system. Because gravitational potential energy depends on relative position, we need a reference level at which to set the potential energy equal to 0. We usually choose this point to be Earth’s surface, but this point is arbitrary; what is important is the difference in gravitational potential energy, because this difference is what relates to the work done. The difference in gravitational potential energy of an object (in the Earth-object system) between two rungs of a ladder will be the same for the first two rungs as for the last two rungs.
Converting Between Potential Energy and Kinetic Energy
Gravitational potential energy may be converted to other forms of energy, such as kinetic energy. If we release the mass, gravitational force will do an amount of work equal to the mgh on it, thereby increasing its kinetic energy by that same amount (ie, converting E to KE).
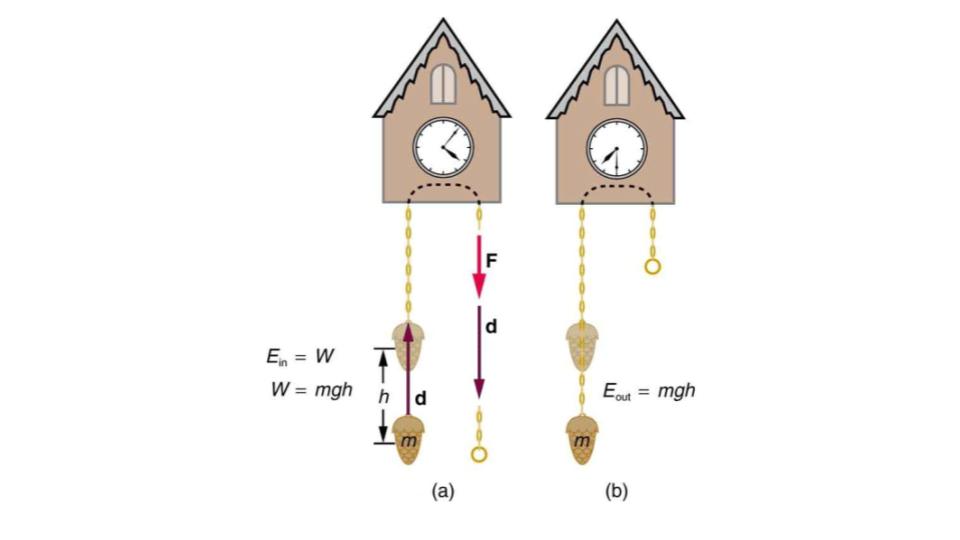
Figure 6.2 (a) The work done to lift the weight is stored in the mass-Earth system as gravitational potential energy. (b) As the weight moves downward, this gravitational potential energy is transferred to the cuckoo clock.
More precisely, we define the change in gravitational potential energy ΔPE to be ΔPE = mgh. You may also see the change in gravitational potential energy written as ΔUg=mgy. These two equations both represent the potential energy due to gravity and can be used interchangeably. In these equations m represents the mass of the object and g represents the gravitational acceleration (9.81m/s2). Both y and h represent the change in height, but y more specifically refers to the change in distance in the y direction.
For example, if a 0.500-kg mass hung from a cuckoo clock is raised 1.00 m, then its change in gravitational potential energy is ΔPE = mgh = (0.500 kg)(9.80m/s2)(1.00 m) = 4.90 kg⋅m2/s2 = 4.90 J.
Law of Conservation of Energy
Energy, as we have noted, is conserved, making it one of the most important physical quantities in nature. The law of conservation of energy can be stated as follows:
Total energy is constant in any process. It may change in form or be transferred from one system to another, but the total remains the same.
Mechanical Energy
Mechanical energy is kinetic energy and any potential energy related to the potential for an object to move. We deal with all other forms of energy by lumping them into a single group called other energy (OE). Then we can state the conservation of energy in equation form as
KEi + PEi + OEi = KEf + PEf + OEf
where subscript i stands for initial and subscript f stands for final.
All types of energy and work can be included in this very general statement of conservation of energy. Kinetic energy is KE, mechanical potential energy is represented by PE, and all other energies are included as OE. This equation applies to all previous examples; in those situations OE was constant, and so it subtracted out and was not directly considered.
LINK TO LEARNING: Use this simulation to see how a skate park applies the conservation of energy and its various properties: PhET Energy Skate Park.
MAKING CONNECTIONS: USEFULNESS OF THE ENERGY CONSERVATION PRINCIPLE
The fact that energy is conserved and has many forms makes it very important. You will find that energy is discussed in many contexts, because it is involved in all processes. It will also become apparent that many situations are best understood in terms of energy and that problems are often most easily conceptualized and solved by considering energy.
When does OE play a role? One example occurs when a person eats. Food is oxidized with the release of carbon dioxide, water, and energy. Some of this chemical energy is converted to kinetic energy when the person moves, to potential energy when the person changes altitude, and to thermal energy OE.
Some of the Many Forms of Energy
What are some other forms of energy? You can probably name a number of forms of energy not yet discussed. Electrical energy is a common form that is converted to many other forms and does work in a wide range of practical situations. Fuels, such as gasoline and food, carry chemical energy that can be transferred to a system through oxidation. Chemical fuel can also produce electrical energy, such as in batteries. Batteries can in turn produce light, which is a very pure form of energy. Most energy sources on Earth are in fact stored energy from the energy we receive from the Sun. We sometimes refer to this as radiant energy, or electromagnetic radiation, which includes visible light, infrared, and ultraviolet radiation. Nuclear energy comes from processes that convert measurable amounts of mass into energy. Nuclear energy is transformed into the energy of sunlight, into electrical energy in power plants, and into the energy of the heat transfer and blast in weapons. Atoms and molecules inside all objects are in random motion. This internal mechanical energy from the random motions is called thermal energy, because it is related to the temperature of the object. These and all other forms of energy can be converted into one another and can do work.
PROBLEM-SOLVING STRATEGIES FOR ENERGY
You will find the following problem-solving strategies useful whenever you deal with energy. The strategies help in organizing and reinforcing energy concepts. In fact, they are used in the examples presented in this chapter. The familiar general problem-solving strategies presented earlier—involving identifying physical principles, knowns, unknowns, checking units, and so on—continue to be relevant here.
Step 1. Determine the system of interest, identify what information is given and what quantity is to be calculated. A sketch will help.
Step 2. Examine all the forces involved and determine whether you know or are given the potential energy from the work done by the forces. Then use step 3 or step 4.
Step 3. If you know that you can apply conservation of mechanical energy simply in terms of potential and kinetic energy, the equation expressing conservation of energy is KEi+PEi=KEf+PEf.
Step 4. You have already identified the types of energy involved (in step 2). Before solving for the unknown, eliminate terms wherever possible to simplify the algebra. For example, choose h=0 at either the initial or the final point, so the gravitational potential energy (PEg) is zero there. Then solve for the unknown in the customary manner.
Step 5. Check the answer to see if it is reasonable. Once you have solved a problem, reexamine the forms of work and energy to see if you have set up the conservation of energy equation correctly. For example, work done against friction should be negative, potential energy at the bottom of a hill should be less than that at the top, and so on. Also check to see that the numerical value obtained is reasonable. For example, the final speed of a skateboarder who coasts down a 3-m-high ramp could reasonably be 20 km/h, but not 80 km/h.
Transformation of Energy
The transformation of energy from one form into others is happening all the time. The chemical energy in food is converted into thermal energy through metabolism; light energy is converted into chemical energy through photosynthesis. In a larger example, the chemical energy contained in coal is converted into thermal energy as it burns to turn water into steam in a boiler. This thermal energy in the steam in turn is converted to mechanical energy as it spins a turbine, which is connected to a generator to produce electrical energy. (In all of these examples, not all of the initial energy is converted into the forms mentioned.)
Another example of energy conversion occurs in a solar cell. Sunlight impinging on a solar cell (see Figure 6.3) produces electricity, which in turn can be used to run an electric motor. Energy is converted from the primary source of solar energy into electrical energy and then into mechanical energy.

Figure 6.3 Solar energy is converted into electrical energy by solar cells, which is used to run a motor in this solar-power aircraft. (credit: NASA)

