3.7 Electromagnetic Energy: Units Conversion
The electromagnetic spectrum encompasses a wide range of wavelengths or energies of light. Scientists working in different disciplines will use units of wavelength or energy that are most convenient for the region of electromagnetic energy in which they work. Different sub-disciplines of science working in the same region of light may also use different units of measurement because of the established convention in their respective fields. For example, an astronomer working in the infrared region plots spectra using wavelength in micrometers, while a geochemist or chemist uses wavenumbers, which is a unit proportional to energy.
It is useful to be able to convert among units so it is possible to compare data among scientific disciplines.
Learning Objectives
- Convert wavelengths of electromagnetic energy between commonly used units.
- Convert the wavelength of electromagnetic energy to wavenumbers (cm-1), a commonly used unit in infrared and Raman spectroscopy.
- Describe the relationships between energy, wavelength, frequency, and wavenumber with the help of Planck’s equation.
Prior Knowledge and Skills
3.2 The Electromagnetic Spectrum
3.3 Wave Behavior
3.6 The Dual Nature of Electromagnetic Energy
Key Terms
- Planck’s constant
- Photon
GuIded Inquiry
Units Conversion: Wavelength
Table 3.7.1. Selected common wavelength units and their symbols.
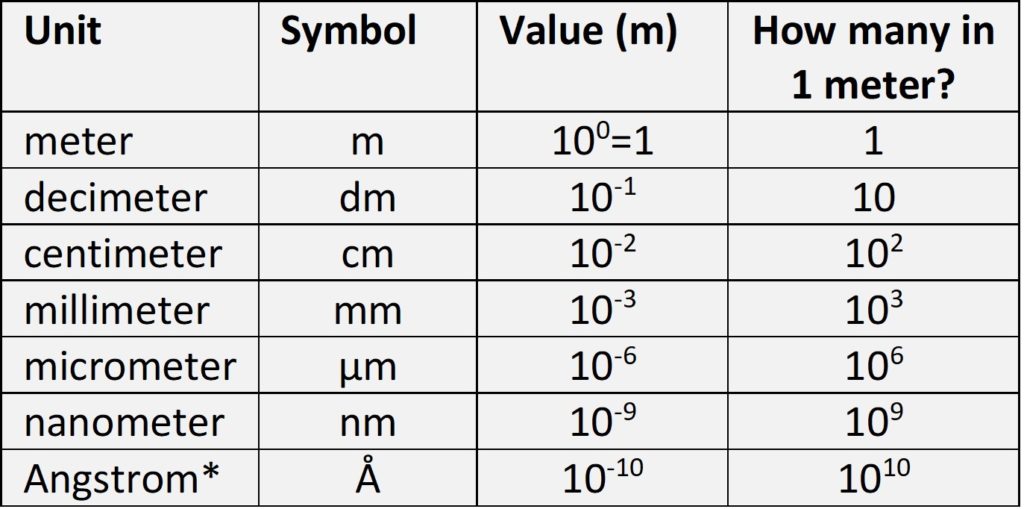
*Angstroms are not a standard unit of length but have been commonly used in the past to describe bond distances and atomic radii in minerals.
3.7.1. Convert orange light with a 630 nm wavelength to units of Angstroms:
3.7.2 Convert orange light with a 630 nm wavelength to units of centimeters:
Units Conversion: Wavelength to Wavenumbers
In 3.6, we saw that electromagnetic energy has characteristics of both a wave and a particle (photon). The Planck equation relates the energy of a photon to its frequency:
Equation 3.7.1. E = hν
Where E = energy, h is Planck’s constant (6.62607004 × 10-34 m2 kg / s), and ν “nu” is the frequency.
We can combine this with Equation 3.2.1 which relates wavelength (λ) and frequency (ν) of electromagnetic energy:
Equation 3.2.1 c = νλ
Where c = 299,792,458 m / s or 3×108 m /s.
Rearranging Equation 3.2.1:
and substituting for ν in Equation 3.7.1 results in:
Equation 3.7.2.
3.7.3. Equation 3.7.2 relates wavelength to energy. Is wavelength proportional to or inversely proportional to energy?
Wavenumber (
) is a common unit used for plotting spectra in the infrared region. Wavenumber is defined as
Equation 3.7.3.
Infrared and Raman spectra are commonly plotted as wavenumbers in units of cm-1.
3.7.4. Is wavenumber proportional to or inversely proportional to energy?
3.7.5. Your astronomer friend reports seeing an absorption band in their measurements at 3 μm wavelength. What is this wavelength in units of wavenumbers (cm-1)?
Summary
Scientists use different units of wavelength and energy depending upon the application and their specific sub-discipline. Spectroscopists use wavenumber as a unit that is proportional to energy and is convenient to compare to wavelength.
There are many web calculators out there- for example, here is a page that converts to several units of energy at once: http://halas.rice.edu/conversions. It is possible to just Google search “convert nanometers to centimeters” and have a calculator pop up in the search results window. However, it is useful to have a working knowledge of the approximate conversions between commonly used units in different fields.
Solution to 3.7.4.
Wavenumber is proportional to energy.
Solution to 3.7.5.
