6.3 The Classical Model: Chemical Bonds as Springs
Elizabeth Johnson
How can we describe the vibrational motions of a molecule? We can think about a diatomic molecule (Figure 6.3.1) as two atoms with masses, and a chemical bond between them as a spring. This is not a perfect analogy, because a spring and two masses at the macroscopic level do not behave in exactly the same way that two atoms connected to each other through chemical bonding will act at the quantum level. But, this analogy is a convenient place to start!

Figure 6.3.1. A model visualizing molecular vibrations. Two atoms are connected by a spring to account for the flexibility of the bond. (Tby11, Creative Commons CC0 1.0 Universal Public Domain).
Learning Objectives
- Describe the motion of a spring.
- Relate the spring constant to the stiffness of a spring.
- Relate the motion of a spring to the frequency or energy of a simple harmonic oscillator.
Prior Knowledge and Skills
3.5 The Dual Nature of Electromagnetic Energy
3.7 Electromagnetic Energy: Units Conversion
6.2 Chemical Bonds Vibrate
Key Terms
- Spring Constant
- Hooke’s Law
- Simple Harmonic Motion
Guided Inquiry
Watch parts of this video:
8.01x – Lect 10 – Hooke’s Law, Springs, Pendulums, Simple Harmonic Motio
https://youtube.com/watch?v=tNpuTx7UQbw%3Ffeature%3Doembed
- From 0:00 to about 4:20 (Spring constant and Hooke’s Law)
- From 8:57 to 11:00 (The connection between simple harmonic motion of a spring and the wave frequency/energy as opposed to amplitude)
Hook’s Law
Hook’s Law is:
[Equation 6.3.1] F = – k x
6.3.1. What is k in this equation?
6.3.2. Compare a stiff spring to a weak spring. Which one would have the higher k, and why? Hint: solve for x in equation 6.3.1 and think about how a higher k would affect the force needed to move the spring the same distance.
Below is the potential energy curve for a spring. As you saw in the video, the spring moves back and forth, or oscillates, in a sinusoidal fashion. This is called a simple harmonic oscillator.
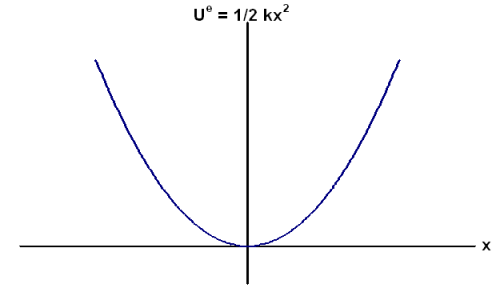
Spring Potential Energy
Interact with a potential energy diagram to see how the potential energy diagram above was created!
Go to this PhET interactive diagram on Hooke’s Law: https://phet.colorado.edu/sims/html/hookes-law/latest/hookes-law_en.html
Choose “Energy” (the third option). Once you are there, choose “Energy Plot” on the right menu. Grab the spring with the claw and move it back and forth!
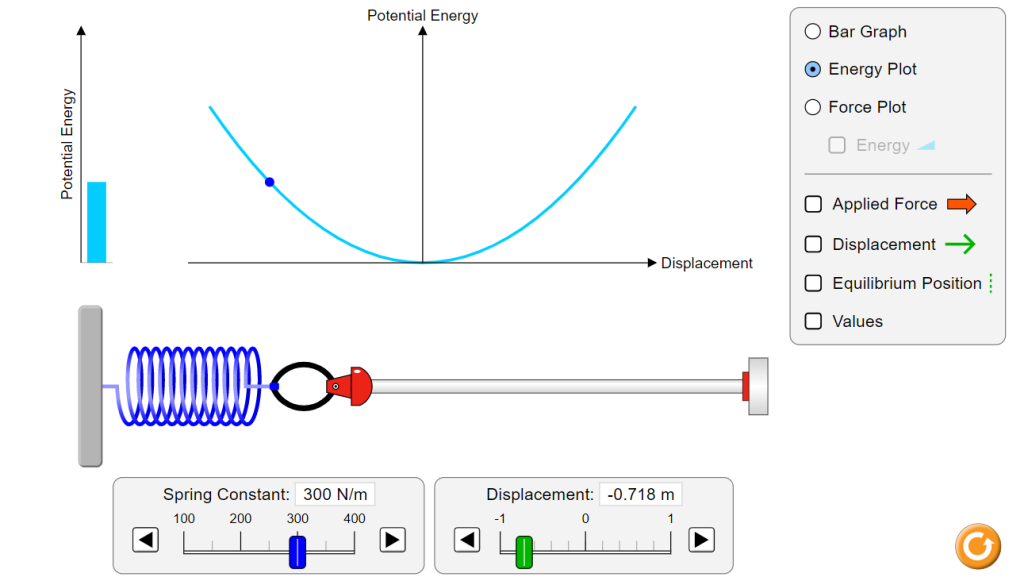
6.3.3. When does a spring have its lowest potential energy?
6.3.4. How does the potential energy curve change if you change the spring constant from 100 N/m to 400 N/m?
Chemical Bonds as Springs
Chemical bonds have (chemical) potential energy, and the potential energy curve of a bond is similar to the potential energy curve of a spring.
Watch the first 4 minutes of this video on bond energy and bond length:
6.3.5. At which point is the bond potential energy (kJ/mol; y-axis) the lowest?
6.3.6. What happens to the bond if the internuclear distance becomes very large?
Concept Check 6.3.7. Why do you think the potential energy curve of a chemical bond shaped diferently from that of a spring? (Hint: what additional force acts upon the atoms at small internuclear distances?)
References
Bozeman Science (Dec 17, 2013) Bond Length and Bond Energy. https://youtu.be/I9jd1Ew_YGU
Elastic potential energy: http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html
PhET. Hooke’s Law. https://phet.colorado.edu/sims/html/hookes-law/latest/hookes-law_en.html
Media Attributions
- Figure 6_3_3 © PhET

