IV. Diatonic Harmony, Tonicization, and Modulation
Extended Tonicization and Modulation to Closely Related Keys
John Peterson
Key Takeaways
- Modulation (sometimes called a “key change”) involves a longer-term change of tonic.
- There are two basic ways a composer can introduce a new key:
- A direct, abrupt modulation (Example 1)
- A pivot chord modulation, which is more subtle (Example 2)
- Sometimes, a composer will blur the lines between a tonicization and a modulation. We refer to such cases as “extended tonicizations.”
We’ve seen that tonicization involves making a non-tonic chord sound like a temporary tonic. In this chapter, we discuss modulation, which, in contrast to the temporary nature of tonicization, involves a longer-term change of tonic. Sometimes people refer to modulation as a “change of key.”
Analyzing Modulations
There are two basic ways a composer can introduce a new key: they can make the key change abrupt (Example 1), or they can be more subtle about it (Example 2). Two pieces of advice are helpful for identifying modulations:
- Remember that cadences establish keys, so if you can identify cadences before you start your analysis, you’ll know where new keys occur.
- The presence of the same accidentals over and over again in a passage is an indication of potential modulation. If you start seeing a consistent accidental, see if you can identify a cadence that establishes the new key corresponding to the change in accidentals.
Direct modulations (these are abrupt)
Abrupt modulations are often called “direct modulations” because the composer goes directly to the new key. These are also sometimes called “phrase modulations” because they tend to occur at phrase boundaries. To recognize a direct modulation in analysis, simply label the new key, then continue with your harmonic analysis as in Example 1.
Example 1. Direct modulation in Joseph Bologne, String Quartet no. 4, I, mm. 15–29 (0:27-0:56).
Pivot chord modulations (these are subtle)
A composer can use a variety of techniques to make a modulation more subtle, but one of the more common ways to do it is through the use of a pivot chord. A pivot chord is a single chord that is diatonic in (i.e., that belongs to) both the home key and the new key. Example 2 shows that we analyze a pivot chord using a special symbol where the upper Roman numeral labels the chord in the old key and the lower Roman numeral labels the chord in the new key. In measure 6 of Example 2, we would say “iv7 becomes ii7.” There’s no single method that always works to find a pivot, but one strategy that’s helpful is to analyze in the old key until it stops making sense, then back up a chord and try analyzing that as your pivot. If that chord doesn’t work as a pivot either, try backing up one more chord.
Example 2. Pivot chord modulation in Josephine Lang, “Der Winter,” mm. 1–12.
Sometimes multiple chords could serve as pivots. In such cases, the best chords are ones where the upper and lower Roman numerals are both predominant chords. That’s because V will usually appear shortly after the pivot, and having a predominant in both positions for your pivot chord label suggests that we’re on the way to V in both the old and new keys. Your second best option would be a tonic chord in the old key becoming a predominant in the new key (I becomes IV). Since a tonic chord can go directly to V, the analysis here still makes functional sense. Poor pivot chord analyses are usually ones that involve the dominant. An analysis such as “V becomes I,” for example, suggests that the same chord is simultaneously unstable (V) and very stable (I), which isn’t how we’re likely to hear it.
Closely related keys
While a composer may modulate anywhere, some modulations are more common than others because of the number of chords the two keys share. Key signatures within one accidental of one another (e.g., C major and G major) are considered closely related keys, sharing many common chords. To find all of the closely related keys for a given home key, do the following. You may find it useful to reference the circle of fifths (Example 3).

- Create a grid with three columns and two rows.
- Place the home key in the center of the upper row.
- Add a sharp (or subtract a flat—the equivalent of adding a sharp) to the home key’s signature and list that key to the right.
- Add a flat to (or subtract a sharp from) the home key’s signature and list that key to the left.
- In the lower row, list the relative major or minor keys for each key in the upper row.
If you were to do this with F major as a starting point, you should end up with something like Example 4. Notice that the keys will always correspond to every major or minor triad in the home key’s universe of Roman numerals (so, in major: I, ii, iii, IV, V, and vi; in minor: i, III, iv, v, VI, and VII). This is a good way to check your work.
| One step flatwise | Starting key signature | One step sharpwise | |
|---|---|---|---|
| starting key | B♭ | F | C |
| relative key | Gmi | Dmi | Ami |
Example 4. Identifying closely related keys of F major.
While it’s possible to modulate to any key, certain keys are much more common than others:
- In major: I→V and I→vi (e.g., C→G and C→Am)
- In minor: i→III and i→v (e.g., Cm→E♭ and Cm→Gm)
Writing modulations with pivot chords
If you’re writing a modulating phrase that uses pivot chords, you’ll need to choose a pivot chord, then determine an appropriate progression.
Identifying potential pivots
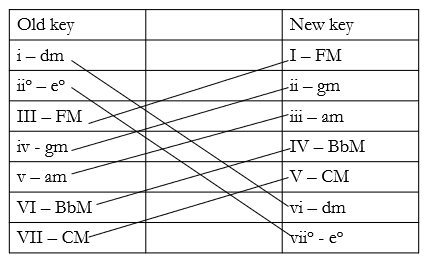
To identify potential pivot chords between two keys (Example 5):
- Create a table with two columns.
- List all triads in the old key on the left.
- List all triads in the new key on the right.
- Match triads that appear in both columns.
Remember that the best pivots are ones that are predominants in both keys.
Example 5. Identifying pivots to modulate from Dm to F.
Choosing a progression
Our ears tend to need time to adjust to hearing a new key. If you want your new key to sound firmly established, it’s therefore best not to cadence too quickly after your pivot. A good strategy can be to use deceptive motion to avoid a cadence in the new key, and then to retry and successfully achieve a cadence afterward (Example 6). Notice that Example 6 begins by establishing the home key with a standard tonic expansion progression.
Example 6. Writing a modulating phrase.
Tonicization versus modulation
Tonicization and modulation can be viewed as two poles on a spectrum based on the length of the passage in question and the strength with which a new key is established (Example 7). Modulations are longer and stronger than tonicization. What does “stronger” mean here? The clearest modulations are those in which the new key is established with the cadence, and then the passage continues in the new key after the cadence. Weaker modulations might only establish the new key with the cadence, then go right back to the home key. Sometimes people will simply hear a passage differently: some people’s ears seem to more willingly accept key changes than others. In your analysis, you should be able to represent your hearing of a given passage and explain why you hear it that way, and you should also be able to understand why someone else might hear it differently.
Example 7. Spectrum between tonicization and modulation.
In between clear tonicizations and modulations is a gray area that we call “extended tonicization.” These are passages like the one in Example 8 where the passage is longer than two chords (longer than, for instance, [latex]\mathrm{V^6_5/V}[/latex] to V), but not so long that it leads to a cadence to establish true modulation. In such cases, we temporarily analyze in a new key, and we show it by placing the Roman numeral of the new key underneath a bracket that underlies the entirety of the extended tonicization. Example 8 begins in E♭ major, then tonicizes F minor, so we put Roman numeral ii under the bracket. In the case of Example 8, the extended tonicization also helps us transition from E♭ major to C minor—in other words, the extended tonicization itself serves as a pivot area.
Often, analysts realize an extended tonicization is taking place when one of two things happens:
- The analyst realizes they have been writing x/ii, y/ii, z/ii over and over again in a short space.
- The Roman numerals stop making functional sense in the home key, but the upcoming cadence is still in the home key.
Example 8. Extended tonicization in Joseph Bologne, String Quartet Op. 4, II (0:25-0:39).
- Extended Tonicization and Modulation to Closely Related Keys (.pdf, .docx). Asks students to review tonicization, identify closely related keys and pivot chords, analyze, and create a modulating progression.
Media Attributions
- Minor Circle of Fifths © Wiki Commons adapted by Bryn Hughes is licensed under a CC BY-SA (Attribution ShareAlike) license
- pivots © John Peterson is licensed under a CC BY-SA (Attribution ShareAlike) license
- spectrum © John Peterson is licensed under a CC BY-SA (Attribution ShareAlike) license
A change of key.
A chord used to modulate between two keys that is diatonic in both.
The process by which a non-tonic triad is made to sound like a temporary tonic. It involves the use of secondary dominant or leading-tone chords.
1. A scale, mode, or collection that follows the pattern of whole and half steps W–W–H–W–W–W–H, or any rotation of that pattern.
2. Belonging to the local key (as opposed to "chromatic").