VIII. 20th- and 21st-Century Techniques
Pitch-Class Sets, Normal Order, and Transformations
Megan Lavengood and Brian Moseley
Key Takeaways
- A pitch-class set (pc set) is a group of pitch classes.
- The standard way of naming a pitch class set is by its normal order: the smallest possible arrangement of pitch classes, in ascending order.
- To transpose a set (Tn), add n to each integer of the set.
- To invert a set (In), first invert the set (take each integer’s complement mod 12), then transpose by n. Alternately, subtract each integer of the set from n (n–x=y).
- The clock face may help you perform any of these tasks.
Pitch-Class Sets
When we talk about a group of pitch classes as a unit, we call that group a pitch-class set, often abbreviated “pc set.” Any group of pitch classes can be a pitch-class set.
Normal Order
Normal order is the most compressed way to write a given collection of pitch classes, in ascending order. Normal order has a lot in common with the concept of root position. Root position is a standard way to order the pitch classes of triads and seventh chords so that we can classify and compare them easily. Normal order does the same, but in a more generalized way so as to apply to chords containing a variety of notes and intervals.
Following are a mathematical and a visual method for determining normal order.
Mathematical method
| Process | Example set: G♯4, A2, D♯3, A4 |
|---|---|
| 1. Write as a collection of pitch classes (eliminating duplicates) such that they would fit within a single octave if played in ascending order. There are multiple possible options. | 8,9,3 |
| 2.Duplicate the first pitch class at the end. | 8,9,3,8 |
| 3. Find the largest ordered pitch-class interval between adjacent pitch classes. | 8 to 9: 1 9 to 3: 6 3 to 8: 5 9 to 3 is the biggest interval. |
| 4. Rewrite the collection beginning with the pitch class to the right of the largest interval and write your answer in square brackets. | [3,8,9] |
Occasionally you’ll have a a tie for largest interval in step 3. In these cases, the ordering that is most closely packed to one side or the other is the normal form. If there is still a tie, choose the set most closely packed to the bottom.
Visual method (clock face method)
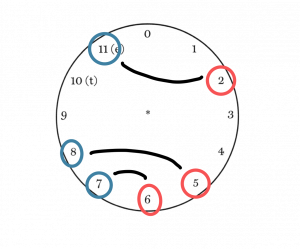
If you don’t like the process described above, the video in Example 1 clearly explains how to use the clock face to quickly find normal order.
Example 1. Using the clock face to find normal form.
Transposition
In post-tonal music, transposition is often associated with motion: take a chord, motive, melody, and when it is transposed, the aural effect is of moving that chord, motive, or melody in some direction. In two disconnected passages from Claude Debussy’s La cathédrale engloutie, the opening motive <D, E, B> or <2, 4, 11> is transposed four semitones higher to <F♯, G♯, D♯> or <6, 8, 3> in m. 18 (both in blue in Example 2), representing the cathedral’s slow ascent above the water. When we hear the passage at m. 18, we recognize its relationship to the passage in m. 1 because the same set of ordered intervals return, but starting on a different pitch. Transposition preserves intervallic content, and not only that, it preserves the specific arrangement of the intervals.
Example 2. Transposition of a motive, ordered and unordered.
The same motive is preserved in a more obscured fashion going from m. 18 into m. 19 (in red in Example 2). Here, the unordered pitch class set is transposed, but not the ordered set from before. This may not look as much like a transposition as the first two sets of motives, but if the pitches are put into normal order, the transposed intervallic relationship becomes clear.
Transposition is often abbreviated Tn, where n, the index number of a transformation, represents the ordered pitch-class interval between the two sets. Transposition is an operation—something that is done to a pitch, pitch class, or collection of these things. Alternatively, transposition can also be a measurement—representing the distance between things.
Transposing a set
To transpose a set by Tn, add n to every integer in that set (mod 12, meaning numbers wrap around after reaching 12, like on a clock face).
Given the collection of pitch classes in m. 1 above and transposition by T4:
[latex]\begin{alignat*}{2}&& [11, 2, 4] \\ {}+ && 4\ 4\ 4\ \\ \hline && [3, 6, 8] \\ \end{alignat*}[/latex]
The result is the pitch classes in m. 18.
T4 [11, 2, 4] = [3, 6, 8]
Identifying transpositions and calculating the index number
To determine the transpositional relationship between two sets, subtract the first set from the second. If the numbers that result are all the same, the two sets are related by that Tn. For example, to label the arrows in Example 1, an analyst would “subtract” the pitch class integers of m. 1 from the pitch-class integers in m. 18. Note that both sets should be in normal order.
[latex]\begin{alignat*}{2} && [3, 6, 8] \\ {}- && [11, 2, 4] \\ \hline && 4\ 4\ 4\ \\ \end{alignat*}[/latex]
[3, 6, 8] and [11, 2, 4] are related by T4.
Inversion
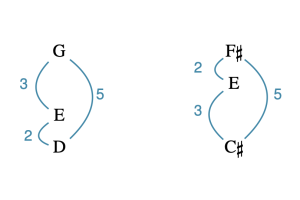
Inversion, like transposition, is often associated with motion that connects similar objects. The passage in Example 3 from Chen Yi’s Duo Ye (2000) is an example: just as in the transpositionally related passages, these two gestures have the same intervallic content, so our ears recognize them as very similar. Unlike transposition, however, the interval content of these two gestures is not arranged in the same way: both have the same intervals, but the [1, 4, 6] set has the interval 3 on the bottom instead of on the top (Example 4).
Example 3. [2, 4, 7] is inverted to become [1, 4, 6].
General inversion
If you are asked to invert a set and are not given an index number, assume you are inverting the set mod 12. This means taking the complement of each number mod 12. The complement of each integer x mod 12 is the number y that is the difference between x and 12. For example, the complement of 4 is 8: 4+8=12. The complement of 6 is 6: 6+6=12. The complement of 0 is 0: 0+0=0, which is 12 mod 12.
Inverting [2, 4, 7] in this way would yield [5, 8, 10].
In: Invert-then-transpose method
Sometimes, sets are inverted and then transposed, as in Example 3. The abbreviation for this is In.
In Example 3, the first set [2, 4, 7] is inverted by I8. To invert a set by I8, follow this process, in this order:
- Invert: [2, 4, 7] becomes [5, 8, 10].
- Transpose: adding 8 to every number in [5, 8, 10] yields [1, 4, 6].
In: Subtraction method
You can calculate the new set created by In by subtracting all the pitch classes of your first set from n.
What is I8 of [2, 4, 7]?
[latex]\begin{alignat*}{2} && 8\ 8\ 8\ \\ {}- && [2, 4, 7] \\ \hline && [6, 4, 1] \\ \end{alignat*}[/latex]
I8 [2, 4, 7] = [1, 4, 6].
Identifying inversions and their index numbers
Any two pitches related by inversion can be added together to form the index number. This makes sense as a logical extension of the subtraction method above: if the inverted pitch y is the result of n–x, then it is also true that n = x + y.
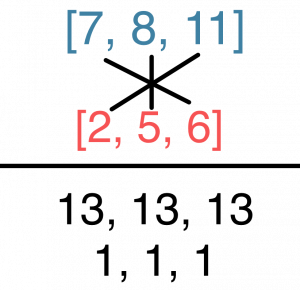
Another way to visualize this is on the clock face. If you have two sets that are 1) both in normal order and 2) related by inversion, the notes within each set will map onto one another in reverse order, as shown in Example 5 below. Write the two sets in normal form on top of one another, then add the opposing integers of each set together as illustrated in Example 6 to yield the index number of the I relation. If the sum of each number pair is 12 or more, subtract 12 so that your n is in mod 12.
Using the Clock Face to Transpose and Invert
If you prefer a more visual method for transposing and inverting, watch the video lesson in Example 7.
Example 7. Using the clock face for transposition and inversion of pitch class sets.
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Normal form and transformations (.pdf, .docx). Asks students to find normal form of various sets, calculate transformations of sets, and identify Tn/In relationships in “Nacht” by Arnold Schoenberg.
- Composition prep worksheet (.pdf, .docx). Prepares students for the set class composition by asking them to find sets and transformations.
Media Attributions
- inversion-2 © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Inversional pairs © Megan Lavengood
- Cross-addition for inversion © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
A group of pitch classes.
A group of pitches that are octave equivalent and enharmonically equivalent.
The most compressed way to write a given collection of pitch classes.
An integer x's complement mod 12 is the number y that would sum to 12. For example, 11's complement mod 12 is 1.
Ordering the notes of a chord so that it is entirely stacked in thirds. The root of the chord is on the bottom.
A group of things that appear in a specified sequence. An ordered pitch set, for example, appears in a consistent order within a piece of music. Compare against a pitch class set, where the pitches are unordered, meaning they can appear in any order in the piece of music.
In a transformation (Tₙ or Iₙ), n is the index number, representing the interval of transposition in semitones.
Short for modulo 12, where numbers wrap around upon reaching 12. Arithmetic in mod 12 is most commonly encountered in clock time: after 12 o’clock, the time becomes 1 o’clock again.