The quality of any sonority can be roughly quantified by summarizing all the intervals it contains. Because all of the intervals contained in a sonority contribute to its overall sound, we must find the interval class (IC) formed by each pitch class in a set, not just those that are next to each other.

Let’s try a simple example first: a C major triad. There are three possible interval classes to be made using the pitch classes of this triad: between its root and third, third and fifth, and root and fifth. C–E is a major third (IC 4), E–G is a minor third (IC 3), and C–G is a perfect fifth (IC 5).

Interval class vectors summarize this as a six-digit number enclosed in angled brackets; each digit corresponds to the count of a certain interval class, as shown in Example 1. The IC vector for the C major triad is <001110>, which shows that the C major triad has:

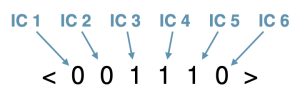
• 0 of IC 1
• 0 of IC 2
• 1 of IC 3
• 1 of IC 4
• 1 of IC 5
• 0 of IC 6

Method

To figure out the interval-class vector, we’re going to simply figure out the interval class created by each combination of two pitches in the sonority. Here is a three-step process for creating an interval-class vector:

1. Write the set in normal form.
2. Find the interval class for every combination of two pitch classes. Record your results on a tally chart.
3. Convert the tallies in each column (including empty columns) to numerals, and enclose these totals in angle brackets < >.

We contain the vector in angled brackets to differentiate it from other strings of integers that might appear in our analysis, like normal form (which gets square brackets) or prime form (which uses parentheses).

Example 2 illustrates this process with the collection of pitches E₄, F♯₄, C₅, and A_5:

1. The normal form of this set is [4, 6, 9, 0].
2. Count each interval class between each pair of pitch classes and keep track using a chart of tally marks:
   1. Begin on the leftmost pitch class (here, 4) and calculate the interval class between it and every pitch class to the right. These interval classes are shown with blue arcs in Example 2.
   2. Move to the right one pitch class (here, 6) and calculate the interval class between it and every pitch class to the right (don’t count to the left, because you already counted that interval class in step 2a). These interval classes are shown with orange arcs.
   3. Move to the right one pitch class (here, 9) and calculate the interval class between it and every pitch class to the right. Because we have a four-pitch-class set, this is the final interval class, shown with a red arc.
3. Converting the tally marks from step 2 into numerals yields the interval-class vector <012111>.

Sets containing a greater number of pitch classes will naturally have more and/or higher numbers in their interval class vectors because there are a lot more intervals at play. Each trichord has three available interval classes (and so the vector should always total to three), each tetrachord has six (and so should sum to six), each pentachord has ten, and so forth.

One way of checking your work after calculating an interval-class vector is to add the number of interval classes up and ensure they total the correct number. If you know the prime form of your set, you can also check against a list of set classes, such as this list from Wikipedia, since they typically include interval-class vectors for each set class.

Example 3 is a video lesson of the above information.

Example 3. Video lesson on interval-class vectors.

Interval-class vectors in analysis

The interval-class vector tells us what intervals a composer may exploit from a particular set, which gives us the set’s particular sound and/or associations. Some sets contain a more or less even distribution of all the interval classes and are especially prized by atonal composers for these properties, while others are especially heavy on one interval class or another and may contain none of a particular interval class.

Interval-class vectors also help us to make aural-analytical connections between two or more sets that may not appear to be immediately related. If they share a similar distribution of interval classes, they will also sound similar in a free-atonal context.

1. Worksheet on Interval-Class Vectors (.pdf, .docx). Asks students to calculate interval-class vectors for several sets.