I. Fundamentals
Minor Scales, Scale Degrees, and Key Signatures
Chelsey Hamm and Bryn Hughes
Key Takeaways
- A minor scale's third note is always a half step lower than the third note of the major scale with the same name.
- There are three variations on the minor scale: natural minor, harmonic minor, and melodic minor.
- Each minor scale is an ordered collection of half and whole steps, as follows:
- Natural minor: W‑H‑W‑W‑H‑W‑W (ascending)
- Harmonic minor: W‑H‑W‑W‑H‑3Hs‑H (ascending)
- Melodic minor: W‑H‑W‑W‑W‑W‑H (ascending) and W‑W‑H‑W‑W‑H‑W (descending).
- While there are three minor scales, minor keys and minor key signatures are always identified as simply “minor” (“A minor,” “D minor,” etc.) and are based on the natural minor scale.
- Scale degrees in minor are the same as those in major. There are a few new solfège syllables in minor including me ([latex]\downarrow\hat3[/latex]), le ([latex]\downarrow\hat6[/latex]), and te ([latex]\downarrow\hat7[/latex]).
- Each note of a minor scale is also named with scale-degree names. These are largely the same in minor as they are in major, except for the subtonic (te or [latex]\downarrow\hat7[/latex]).
- Major and minor keys share two different relationships. The parallel relationship is when a major and minor key share a tonic note, while the relative relationship is when a major and minor key share a key signature.
- Each major key signature has a corresponding relative minor key signature whose tonic is three half steps below the relative major’s tonic. The orders of sharps and flats in major and minor key signatures are the same.
The Minor Scale
A minor scale's third note is always a half step lower than the third note of the major scale with the same name (e.g., B major and B minor). There are three different types of minor scales: natural minor, harmonic minor, and melodic minor. These three types of minor scales should be thought of like flavors of ice cream; ice cream is still ice cream regardless of whether it is chocolate, vanilla, strawberry, etc. Likewise, a work is simply “minor” or “in minor”; musicians do not consider music to be “in” a specific type of minor scale (i.e., natural, harmonic, or melodic). In other words, while there are three minor scales, minor keys and minor key signatures are always identified as simply “minor” (“A minor,” “D minor,” etc.) and are based on the natural minor scale.
The three different types of minor scales are useful categories primarily for instrumental performers. Learning to play the different types of minor scales on instruments allows performers to become familiar with the minor patterns most commonly used in Western classical music. Just like major scales, minor scales are named for their first note (including the accidental, if any), which is also their last note.
Natural Minor
The natural minor form of the minor scale consists of an ordered collection of half and whole steps with the ascending succession W‑H‑W‑W‑H‑W‑W, as shown in Example 1. Each whole step is labeled with a square bracket and “W,” and each half step is labeled with an angled bracket and “H.” Listen carefully to Example 1 and notice that the half and whole step pattern of the natural minor form of the minor scale is the same ascending and descending.
Example 1. A G natural minor scale. (Sounding scale is F natural minor.)
Harmonic Minor
The harmonic minor form of the minor scale consists of an ordered collection of half and whole steps in the ascending succession W‑H‑W‑W‑H‑3Hs‑H (“3Hs” = 3 half steps), as shown in Example 2. The curved bracket represents a distance of three half steps (or a whole step plus a half step). Listen carefully to Example 2 and notice that the half and whole step pattern of the harmonic minor form of the minor scale is the same ascending and descending.
Example 2. A G harmonic minor scale. (Sounding scale is F harmonic minor.)
Melodic Minor
The melodic minor form of the minor scale consists of an ordered collection of half and whole steps in the ascending succession W‑H‑W‑W‑W‑W‑H and the descending succession W‑W‑H‑W‑W‑H‑W, as shown in Example 3. When you listen to Example 3, notice that the melodic minor form has different ascending and descending patterns: the ascending pattern is unique to the melodic minor form, while the descending pattern is the same as the natural form.
Example 3. A G melodic minor scale. (Sounding scale is F melodic minor.)
Example 4 shows four versions of a C scale—major, natural minor, harmonic minor, and melodic minor—with the scale degrees indicated. Listen to this example carefully, noting the aural differences between the scales.
Example 4. Major, natural minor, harmonic minor, and melodic minor scales, all starting on C.
Minor Scale Degrees, Solfège, and Scale-Degree Names
Minor scale degrees, solfège, and scale-degree names are similar to, but not exactly the same as, their major-scale counterparts. Example 5 summarizes the three types of minor scale, and shows the scale degrees and solfège for each. Note that the scale degrees are the same as in a major scale. The bottom line shows the solfège syllables, which differ from the major-scale syllables in several places to reflect the minor scale’s pattern of whole and half steps.
Example 5. Scale degrees and solfege for all three types of minor scales: a) natural minor; b) harmonic minor, and c) melodic minor.
In natural minor (Example 5a), mi ([latex]\hat{3}[/latex]) becomes me ([latex]\downarrow\hat3[/latex]) (pronounced “may”), la ([latex]\hat{6}[/latex]) becomes le ([latex]\downarrow\hat6[/latex]) (pronounced “lay”), and ti ([latex]\hat{7}[/latex]) becomes te ([latex]\downarrow\hat7[/latex]) (pronounced “tay”). If you sing or play through the above example, you’ll notice that the ending lacks the same sense of closure you heard in the major scale. In the major scale, this closure is created in part by the ascending semitone between ti ([latex]\hat{7}[/latex]) and do ([latex]\hat{1}[/latex]).
In harmonic minor (Example 5b), mi ([latex]\hat{3}[/latex]) becomes me ([latex]\downarrow\hat3[/latex]) and la ([latex]\hat{6}[/latex]) becomes le ([latex]\downarrow\hat6[/latex]). Having ti ([latex]\hat{7}[/latex]) creates the sense of closure that is absent in the natural minor scale.
As noted above, the melodic minor scale has different ascending and descending patterns (Example 5c). In the ascending form of melodic minor, mi ([latex]\hat{3}[/latex]) becomes me ([latex]\downarrow\hat3[/latex]), but the rest of the solfège syllables are the same as in major. In the descending form of melodic minor, mi ([latex]\hat{3}[/latex]) becomes me ([latex]\downarrow\hat3[/latex]), la ([latex]\hat{6}[/latex]) becomes le ([latex]\downarrow\hat6[/latex]), and ti ([latex]\hat{7}[/latex]) becomes te ([latex]\downarrow\hat7[/latex]), like natural minor. Therefore, the ascending version of melodic minor has the sense of closure associated with the major scale, while the descending version follows the pattern of the natural minor scale.
As in major scales, each note of a minor scale is also named with scale-degree names. Example 6 shows the scale-degree names used in minor scales alongside the corresponding scale-degree numbers and solfège syllables.
| Scale Degree Number | Solfège | Scale Degree Names |
|---|---|---|
| [latex]\hat1[/latex] | do | Tonic |
| [latex]\hat2[/latex] | re | Supertonic |
| [latex]\downarrow\hat3[/latex] | me | Mediant |
| [latex]\hat4[/latex] | fa | Subdominant |
| [latex]\hat5[/latex] | sol | Dominant |
| [latex]\downarrow\hat6[/latex] | le | Submediant |
| [latex]\downarrow\hat7[/latex] | te | Subtonic |
| [latex]\hat7[/latex] | ti | Leading Tone |
Example 6. Scale-degree names in minor scales.
As the chapter on major scales discussed, the Latin prefix sub means “under”—the submediant is a third below the tonic, and the subdominant is a fifth below. To this, we can now add one new scale degree name: the subtonic, for lowered [latex]\downarrow\hat7[/latex]. The supertonic is one whole step above the tonic, while the subtonic is one whole step below the tonic.
Example 7 shows a B melodic minor scale, ascending and descending, with scale-degree names labeled. As you can see, the melodic minor scale utilizes the leading tone in its ascending form, and the subtonic in its descending form.
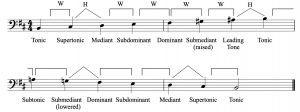
Example 8 is a helpful visual for learning about the three forms of the minor scale. The order reflects the number of lowered scale degrees (compared to a major scale starting on the same note).
| Form of Minor Scale | Lowered Scale Degrees |
|---|---|
| Natural | [latex]\downarrow\hat{3},\downarrow\hat{6}, \downarrow\hat{7}[/latex] |
| Harmonic | [latex]\downarrow\hat{3},\downarrow\hat{6}[/latex] |
| Melodic (ascending) | [latex]\downarrow\hat{3}[/latex] |
Example 8. Lowered scale degrees of minor.
As you can see, natural minor scales have three lowered scale degrees, harmonic minor scales have two, and melodic minor scales have one in the ascending version. Remember, the descending version of melodic minor is the same as natural minor, with three lowered scale degrees.
The Parallel and Relative Relationships
When comparing major and minor keys, there are two relationships that are important. The parallel relationship is when a major key shares a tonic (do, [latex]\hat{1}[/latex]) with a minor key. For example, C major and C minor (or A♭ major and A♭ minor, or F♯ major and F♯ minor) are parallel keys. We use the terms “parallel minor” and “parallel major” to describe this relationship: C major is the parallel major of C minor, and C minor is the parallel minor of C major.
The relative relationship is when a major key shares a key signature with a minor key. For example, C major does not have any sharps or flats in its key signature, and neither does A minor. We use the terms “relative minor” and “relative major” to describe this relationship: C major is the relative major of A minor, and A minor is the relative minor of C major. The tonic of a minor key is always three half steps below the tonic of its relative major: if you count three half steps below C, you will get A (C–B, B–B♭, B♭–A). Likewise, to find the relative major key of a given minor key, count three half steps up.
When counting half steps to determine the relative major or minor of a given key, keep in mind that relative keys have the same key signature. A sharp key cannot share a relative relationship with a flat key (and vice versa), which means you need to select the correct enharmonic key. For example, although the pitch three half steps down from D♭ could be written as either B♭ or A♯, only B♭ minor (five flats) is the relative minor of D♭ major (also five flats), because A♯ minor has a different key signature (seven sharps).
Minor Key Signatures
Minor key signatures, like major key signatures, go after a clef but before a time signature. Each major key has a corresponding relative minor key signature; therefore, the orders of the sharps and flats are the same in minor key signatures as they are in major key signatures, placed on the same lines and spaces. Example 9, reproduced from the previous chapter, shows the order of sharps and flats in all four clefs:

As previously mentioned, if you know the major key associated with a given key signature, you can go down three half steps from the tonic to find the minor key for that key signature. Example 10 shows all of the sharp minor key signatures in order, and Example 11 depicts all of the flat minor key signatures in order.
- Example 10. The key signatures of A, E, B, F♯, C♯, G♯, D♯, and A♯ minor.
- Example 11. The minor key signatures of A, D, G, C, F, B♭, E♭, and A♭ minor.
Minor keys can also be imaginary (like imaginary major keys) if they contain double accidentals.
You can practice identifying minor key signatures in the following exercise:
Minor Keys and the Circle of Fifths
The circle of fifths can be used as a visual for minor key signatures as well as major key signatures. Each key signature is placed alongside the corresponding major and minor keys. Example 12 shows the circle of fifths for minor and major keys:
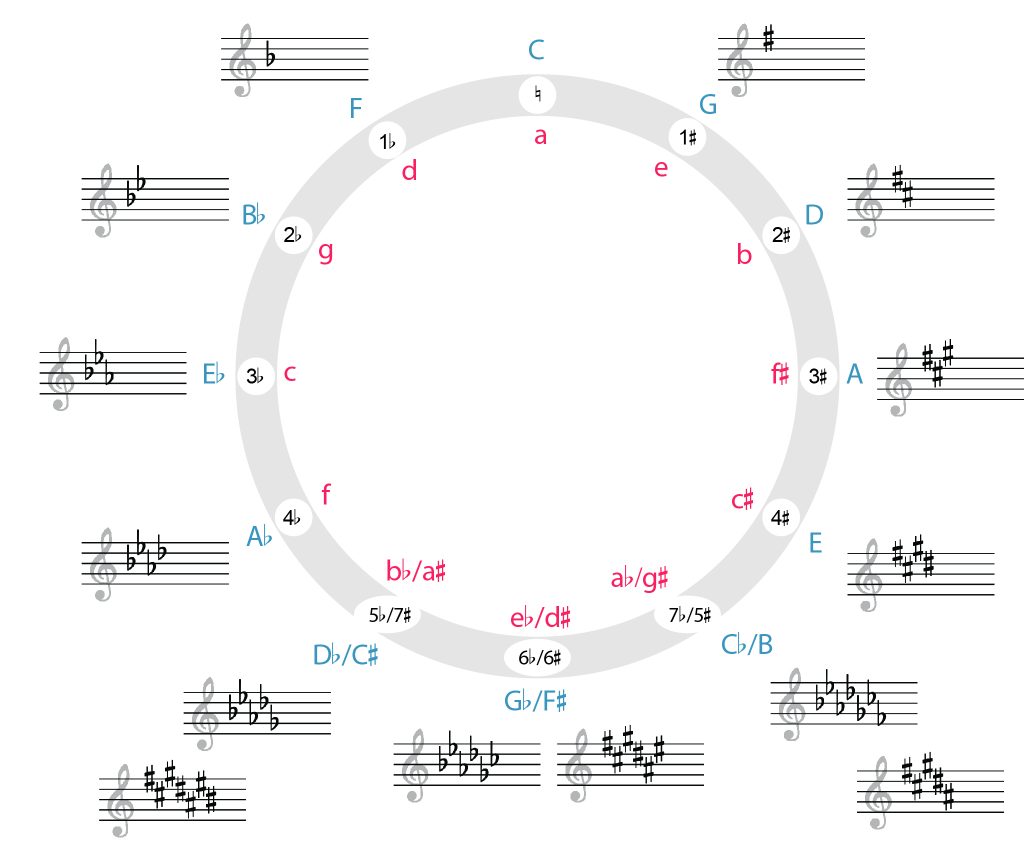
In Example 12, major keys are in blue uppercase letters around the outside of the circle, while minor keys are in red lowercase letters around the inside of the circle. Once again, key signatures appear in order of their number of accidentals. If you start at the top of the circle (12 o’clock) and continue clockwise, key signatures add sharps, while if you start at the top of the circle and continue counterclockwise, they add flats. The bottom three key signatures can be written in sharps or flats, and so are enharmonic.
Major or Minor?
When you are given a piece of music to play or sing, the notation will often include a key signature, which will help you to narrow down the key of the work to two options: a major key and its relative minor.[1] But how can you tell which one the work is in? One thing that can help is to listen to and look at the first and last notes of the work—pieces often start and end on the tonic, so this can help you determine whether a work is major or minor.
Example 13 shows the first three measures of a song by Louise Reichardt (1779–1826) titled “Durch die bunten Rosenhecken” (“Through the colorful rose hedges”):

This example shows a vocal line (the top staff) and a piano part (the grand staff underneath the vocal part). The key signature contains four flats, which means we can narrow down the key of this work to A♭ major or F minor. In Example 13, the first note that is circled in the highest part (the vocalist) is is F, as is the first note that is circled in the lowest part (the lowest note played by the piano). Therefore, it is likely that the key of this work is F minor instead of A♭ major.
- Minor Scales Tutorial (musictheory.net)
- Minor Scales (Practical Chords and Harmonies)
- Minor Scales (YouTube)
- Scale Degree Names in Major and Minor (musictheory.net)
- Minor and Major Key Signatures (musictheory.net)
- Minor Key Signatures (YouTube)
- Minor Key Signature Flashcards (music-theory-practice.com) (be sure to click “minor” in the menu)
- The Circle of Fifths for Minor and Major (YouTube)
- The Circle of Fifths (Classic FM)
- Natural Minor Scales (.pdf)
- Harmonic Minor Scales (.pdf)
- Melodic Minor Scales (.pdf)
- Writing Minor Scales (.pdf, .pdf)
- Writing Minor Key Signatures (.pdf)
- Writing and Identifying Minor Key Signatures (.pdf)
- Parallel and Relative Minor Questions (.pdf)
- Scale Degree Names and Scale Degrees (.pdf)
Media Attributions
- Scale-degree Names Minor © Chelsey Hamm is licensed under a CC BY-SA (Attribution ShareAlike) license
- Sharps and Flats in Different Clefs © Chelsey Hamm is licensed under a CC BY-SA (Attribution ShareAlike) license
- Minor Circle of Fifths © Wiki Commons adapted by Bryn Hughes is licensed under a CC BY-SA (Attribution ShareAlike) license
- Durch die bunten Rosenhecken © Louise Reichardt is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- The vast majority of Western classical works from 1700–1900 are in either major or minor. But outside of this time period and cultural context, you should also consider if the piece may be in a diatonic mode. This would expand the number of possible tonics indicated by a key signature. ↵
An ordered collection of half steps and whole steps.
An ordered collection of half steps (H) and whole steps (W) with the ascending succession W–H–W–W–H–W–W.
An ordered collection of half and whole steps with the ascending succession W–H–W–W–H–3Hs–H. Like natural minor, but with a raised 7̂.
An ordered collection of half steps (H) and whole steps (W) with the ascending succession W–H–W–W–W–W–H and the descending succession W–W–H–W–W–H–W.
The relative position of a note within a diatonic scale. Indicated with a number, 1–7, that indicates this position relative to the tonic of that scale.
The application of solmization syllables (do, re, mi, fa, sol, etc.) to scale degrees.
A movable system of names for scale degrees based on their function within the scale, such as tonic (do, 1̂) and dominant (sol, 5̂).
When two keys/scales share the same pitches.
In music notation, a collection of sharps or flats written at the beginning of each line (immediately after the clef) to signal that certain notes are always sharp/flat.
An ordered collection of half steps (H) and whole steps (W) as follows (ascending): W–W–H–W–W–W–H.
A relationship between notes, intervals, or chords that sound the same but are spelled differently.
A graphic that shows the relationship between major (and/or minor) key signatures by placing the key signatures around a circle in order of number of accidentals.



