Chromatic Modulation

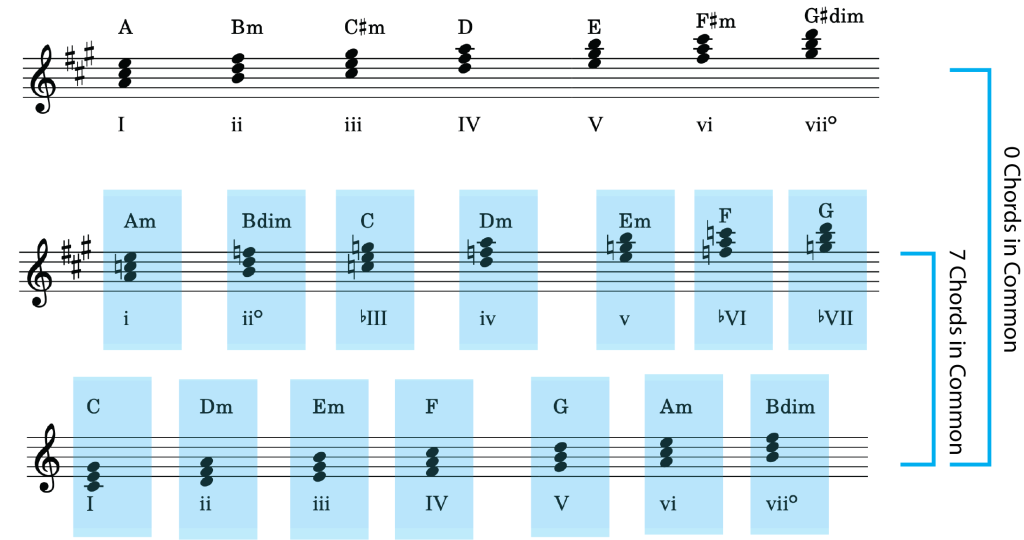
Modulation to closely-related keys is a relatively easy task; we can find a pivot chord by looking at the group of chords shared between two keys that have nearly-identical key signatures. There are plenty of them. See Example 1: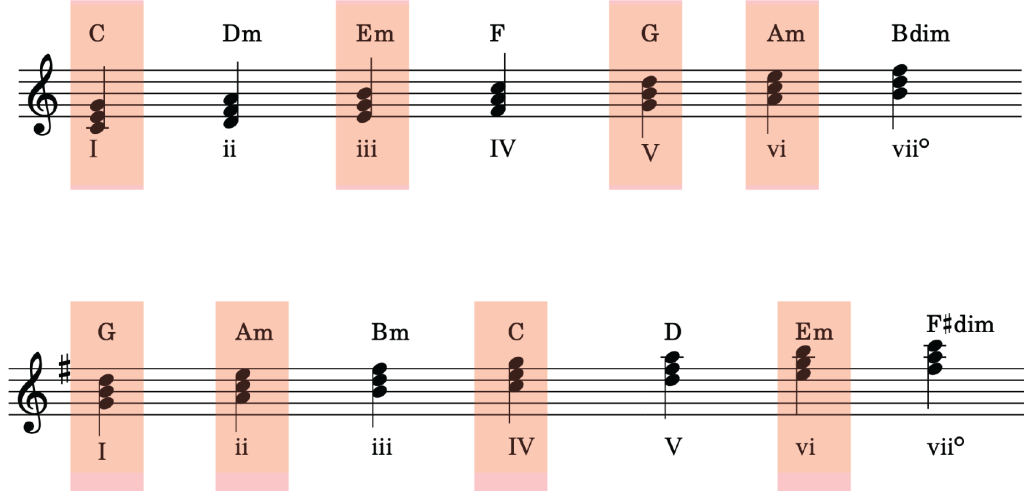

Example 1. Common chords in the keys of C and G major.

When two keys are more than one accidental apart on the circle of fifths, however, it becomes more difficult it is to find a pivot chord that will enable a smooth modulation between the two keys.

To modulate to a distantly-related key, that is, a key that is more than one accidental away on the circle of fifths, requires us to use our knowledge of chromatic chords, such as those found through mode mixture. Mode mixture enables us to expand the number of possible pivot chords for modulation. For example, in the key of C major, the chords made possible through mode mixture (i.e. those chords found in C minor, its parallel key), we can now modulate easily to E-flat major (7 shared chords), A-flat major (4 shared chords), B-flat major (3 shared chords), and their relative minor keys, F minor and G minor. Example 2 shows the common chords shared between C major and E-flat major, made possible by using mixture chords in C major.

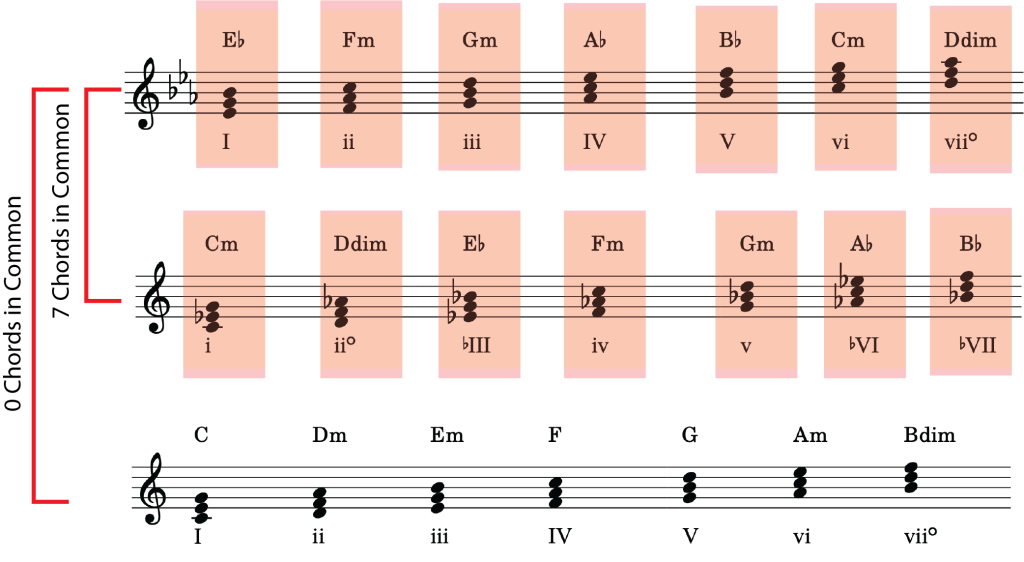Example 2. Shared chords between C major and E♭ major, made possible through mode mixture. 

Example 3 shows a modulation from the key of A major to F major, using iv from A major as a pivot chord. Example 4 shows this technique being used by Verdi in his opera Rigoletto.

Example 3. Modulation from A major to F major using a mixture chord in A major (iv) as a pivot chord. 

Example 4. Modulation from D♭major to F♭ major using a mixture chord in D♭ major (♭VI⁶) as a pivot chord. 

Conversely, we can use diatonic chords in the old key as mixture chords in the new key to modulate to distant keys in the “sharpwise” direction on the circle of fifth. Example 5 shows the potential pivot chords when modulating from C major to A major by way of the diatonic chords in C major as mixture chords in the new key of A major.

Example 5. Potential pivot chords when modulating from C major to A major. 

A modulation using this technique in a chorale setting is shown in Example 6.

Example 6. Modulation from A♭ major to C major using a diatonic chord in A♭ major (vi) as a pivot chord that is interpreted as a mixture chord (iv) in C major. 

Example 7 shows an interesting chromatic modulation from Brahms’s Waltz, op. 39, no. 14. Here, Brahms uses a diatonic vii^o6 chord in the local key of G major to pivot to E major, reinterpreting the chord as ii^o6, a mixture chord in the new key of E major.

Example 7. Modulation from G major to E major using a diatonic chord in G major (viio6) as a pivot chord that is interpreted as a mixture chord (iio6) in E major. 

Common-Tone Modulation

Sometimes we can use a common-tone, rather than a pivot chord, to modulate to distantly related keys. In particular, the key areas that are a third away from the home key are easily modulated to using this technique.These keys, chromatically altered tonics that are a third away from the home key, are called “chromatic third” or “chromatic mediant” relations. For example: C and A♭ major (share the common tone C), C and E♭ major (share the common tone G), C and A major (share the common tone E), C and E major (share the common tone E). These relationships are shown in Example 8.

Example 8. Common tones shared between chromatic mediants. 

In the song “Widmung,” Robert Schumann uses precisely this technique to modulate from Ab major to a chromatic-mediant related key, Fb major (written as E major for clarity). In Example 9, we can see the key of A♭ clearly confirmed by way of a PAC in m. 13. Our ears hang on to the A♭ arrival, which is then reinterpreted as a G♯, the third of the tonic chord in E major, which is confirmed a few measures later.

Example 9. Robert Schumann, Op. 25 No. 1, “Widmung,” mm. 10-17

Enharmonic Reinterpretation

In the previous example, the note A♭ was reinterpreted as G♯, which became the third of the tonic chord in the key of E major. Enharmonic equivalence (and the reinterpretation made possible by this equivalence) enables us to open up numerous possibilities for modulating into distantly related keys. One such equivalence that you may have noticed already is that between the dominant-seventh and the German augmented-sixth chord.

Example 10. Respelling German augmented-sixths as dominant sevenths, and vice versa

Example 10 provides two examples of how a dominant seventh can be reinterpreted as a German augmented-sixth chord, and vice versa. In Example 10 a), the seventh resolves downward by step to the third of the tonic chord, while the bass leaps to the root of the tonic chord. Following this, the B♭ is reinterpreted as A♯, and resolves up by step. Along with the bass moving down by step, these two pitches resolve to [latex]\hat{5}[/latex], supported by a cadential six-four in the key of E major. This difference in voice leading (seventh resolving down by step, augmented sixth resolving outward to [latex]\hat{5}[/latex]) is the fundamental distinction between a dominant seventh chord and  its enharmonically equivalent German augmented sixth.

Example 11 shows this kind of enharmonic reinterpretation in action. The violin soloist plays a long cadenza over a dominant-seventh chord in the key of C major. When the orchestra joins in again, they confirm the dominant harmony, but when the chord resolves, the F natural in the solo violin moves upward by half step, to F♯, and the G in the cellos and basses resolves down by half step to F♯. In this moment, the G-F minor seventh is reinterpreted as a G-E♯ augmented sixth, resolving to the dominant in B minor. This harmony is filled out in the next few measures, confirming a dominant chord F♯ major in m. 304.

Example 11. Beethoven, Concerto in D Major for Violin and Orchestra, Op. 61, I, mm. 280-304

So, if you reinterpret a dominant-seventh chord as an augmented-sixth chord and use it to pivot into a new key, the resulting modulation will be down a half step. Conversely, if you reinterpret an augmented-sixth chord as a dominant-seventh chord, the resulting modulation will be up a half step. Example 12 shows precisely this. Here, Haydn spends three measures on the German augmented-sixth chord in the key of D major (B♭-D-F-G♯), allowing the audience to ruminate on the harmony through the use of a fermata. Instead of resolving the chord in D major, the G♯ is reinterpreted as an A♭ and it resolves down by half step to the third of the new tonic of E♭ major.

Example 12. Haydn Piano Trio in D Major, Hob. XV: 16, I, mm. 163-73

You can, of course, use this trick with any dominant-seventh chord (say, a secondary dominant), opening up numerous possibilities for modulation. Example 13 shows Schubert reinterpreting a German augmented-sixth chord as a V⁷/IV chord to pivot from the key of C♯ major to A major (another instance of a modulation to a chromatic mediant-related key!).

Example 13. Schubert, Valses Sentimentales, Op.50, No. 13 (D.779), mm. 18-38

Reinterpreting Diminished-Seventh Chords

Like the dominant-seventh/German augmented-sixth, the diminished-seventh chord can be enharmonically respelled to serve as a pivot chord into distantly related keys. This is because of its symmetrical nature: the diminished-seventh chord divides the octave into four equal parts (each a minor third apart), and is thus limited in possible transpositions. Practically speaking, this means that any note in a diminished-seventh chord can be interpreted as the root of the chord. In Example 14, you can see a B diminished-seventh chord interpreted with each of its chord members functioning as the root. Although you would be playing the same four keys on the piano in the same position, this gives the impression that the pivot chord is “changing inversion”; this is because the new interpretation changes how we hear the sounding bass note.

Example 14. Diminished-Seventh Chord Respellings

A classic example of this technique can be found in Beethoven’s Piano Sonata in C minor, Op. 13, found in Example 15. In this passage, Beethoven uses several diminshed-seventh chords. The first one that we hear behaves normally, functioning to tonicize the dominant. The second time we hear a diminished-seventh chord, we hear the one local to the key of G minor: F♯-A-C-E♭. This one also behaves as we expect it to, resolving to a tonic chord in first inversion. We hear the same chord again in the following measure, but this time Beethoven spells the chord F♯-A-C-D♯. The new spelling reflects the chord’s new function, with D♯ serving as the leading tone in the new key of E minor.

Example 15. Beethoven, Piano Sonata in C minor, Op. 13, I, mm. 133-39.

You can, of course, use this technique with any diminished-seventh chord, not just the one diatonic in the local key. In Example 16, Brahms set up an expectation that the diminished-seventh chord in measure 5 will tonicize the dominant. This expectation is set through the extended tonicization heard in the previous measure, where we first hear this diminished-seventh chord. In measure 4, the chord is spelled A-C-E♭-G♭, and functions as viio7 of the dominant in E♭ major. In measure 5, we hear this chord again. Our expectations are thwarted, however, as the chord instead resolves to a G minor triad in first inversion. Brahms gives us a clue that this may happen by spelling this chord differently (despite the fact that it is enharmonically equivalent): A-C-E-F♯. It is spelled with the intended resolution to G minor in mind, as F♯ is the leading tone in the new key. G minor indeed becomes the new tonic, which is confirmed by a cadence a few measures later.

Example 16. Brahms, Op. 57, No.2

Conclusion

In summary, the examples above have shown that both diminished-seventh chords, along with dominant-seventh/augmented-sixth chords, are much more tonally flexible than you may have thought when you first learned about them. These chords can serve as gateways into distant keys, allowing composers to freely navigate through tonality both quickly and elegantly.

1. Respelling, Part-Writing, and Analysis (PDF), (Word), (Musescore)