Chapter Playlist

“Dissonance” is one of those multi-purpose terms with a range of uses both within and beyond musical analysis. Outside of music, terms such as cultural or cognitive dissonance usually have negative connotations, but music has a way of making a virtue of the “wrong” or “ill-fitting.” Musical dissonance is not “bad” in the same sense as some of these other contexts (though stylistic norms may require proper handling and resolution, at least in the case of tonal counterpoint).

These same notions of consonance and dissonance have been applied to meter.^[1] The modern conception of metrical dissonance was galvanized by Harald Krebs (1999).^[2] This chapter is based on Krebs’s theory, and categorizes metrical dissonance as either displacement dissonance or grouping dissonance, each of which is discussed further below.

Displacement Dissonance

Displacement dissonance occurs when one layer of the music seems to be out-of-sync with the surrounding context. Example 1 uses a familiar tune to illustrate: in 1a, the tune is in sync with the bass line; in 1b, it is an eighth note “late.” Example 1b then is an example of displacement dissonance. Note that the final note of 1b arrives properly in sync with the bass; this kind of adjustment is common in real pieces as well, especially to create a sense of conclusion or arrival (e.g., at cadences). This is a simple example of displacement dissonance: when two layers imply the same meter, but one is offset from the other by a consistent rhythmic value. This rhythmic value is called the displacement index; so, the displacement index of Example 1b is +1♪.

Example 1. Illustration of displacement dissonance.

Listening to Examples 2a and 2b, one would likely default to beginning these passages on beat 1 of a [latex]\mathbf{^3_4}[/latex] measure, creating four bars of [latex]\mathbf{^3_4}[/latex]. In the actual piece these lines are drawn from—Marie Jaëll’s Impromptu—the two lines occur simultaneously, but the melody is offset from the bass line, moved forward by one eighth note (again, a displacement index of +1♪).

Example 2. Displacement dissonance (+1♪) in Marie Jaëll’s Impromptu (1869; 4:43).

Example 3 provides another example from the B section (at 1:45 and 2:36, to the lyrics “you just call on me, brother, when you need a hand”) of Bill Withers’s iconic “Lean on me” (1972). In the A section of this song, the meter and grouping are clear and set the listener’s metric expectations. In the B section, the hand claps create a strong sense of displacement dissonance. Hand claps are typically a snare-drum substitute in pop drumbeats, playing the backbeat on beats 2 and 4 of a quadruple meter. But here, the handclaps are on the 2nd and 6th eighth notes of the bar, suggesting a backbeat that occurs an eighth note early (−1♪).^[3] The song’s overarching meter may never be in doubt, but the rhythmic-metrical richness of this passage can be helpfully understood in terms of the systematic syncopations that potentially point to alternative displacements of the meter.

Example 3. Displacement dissonance (−1♪) in Bill Withers’s “Lean on me” (2017; 1:45). Brackets indicate the displacements discussed in the text.

Grouping dissonance

Grouping dissonance is the combination of two layers with different internal grouping organization; more specifically, the two layers articulate groupings with different numbers of pulses (pulse cardinalities), and these cardinalities are not multiples/factors of one another. These layers can be referred to in terms of their cardinalities to distinguish them: for example, a “3-layer” and a “4-layer.” Example 4 provides simple illustrations of grouping dissonance.

Example 4. Illustration of grouping dissonances.

The juxtaposition of 2- and 3-layers as in Example 4a is common enough to be known by a special name: the hemiola. The hemiola is a grouping dissonance found even in early Western concert music, such as G.F. Handel’s Water Music Suite No. 2, mvt. II (“Alla hornpipe”), shown in Example 5. This sort of hemiola is often found at important cadences of pieces in triple meter, where two measures of triple meter (a 3-layer) can be interpreted as three groups of two beats (a 2-layer) instead. This dissonance heightens excitement and reinforces the sense of tension-and-release created by the familiar cadential harmonic progression.

Example 5. A hemiola in Handel’s “Alla hornpipe” (Water Music Suite No. 2, mvt. II; 1733). The 2-layer implied in the surface rhythms of mm. 9–10 (red) create grouping dissonance with the 3-layer of the meter.

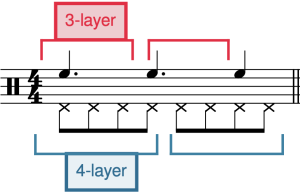
Three-against-four (3:4) is another widespread rhythmic-metrical pattern that can be readily heard in terms of grouping dissonance. Example 4b sets out a complete cycle of this grouping dissonance, but partial cycles are more common in musical practice, especially in pop music—from classic jazz to electronic dance music (EDM). The Afro-Cuban tresillo rhythm can be viewed as a partial cycle of the 3-against-4 dissonance (Example 6).

Example 7 shows a partial 3:4 grouping dissonance (sixteenth-note pulse) from Calvin Harris’s “I’m Not Alone” (2009). The song’s overall simple quadruple meter is clear from the four-on-the-floor kick drum and handclap on the backbeat, but the synth and bass riffs creates metrical dissonance out a conflicting pattern based on groupings of three sixteenth notes. Note that the 3-layer breaks off with a 2-pulse-long grouping so that the riff has a downbeat arrival on every other measure.

Example 7. A 3-layer in the synth and bass create grouping dissonance with the 4-layer in the meter and drumbeat in Calvin Harris’s “I’m Not Alone” (2009; 0:59). 

Grouping dissonances and polyrhythms can often be easier to understand in box notation rather than traditional Western notation, which prioritizes metrical hierarchies in a way that might not be helpful when dealing with grouping dissonance. Example 8 is a box notation diagram illustrating “I’m Not Alone.” In Western notation, we are forced to choose between unusual dotted rhythms or very frequent ties, both of which have advantages and disadvantages, but in box notation, this issue is entirely circumvented. The box notation also clarifies the mathematical properties of grouping dissonances. Any grouping dissonance will have a point of realignment, where both layers have a simultaneous attack point. This happens after x number of pulses, where x is the lowest common multiple between the cardinalities of the two layers. 12 is the lowest common multiple between 3 and 4, so a 3:4 grouping dissonance realigns every twelve pulses.

Grouping dissonance via ostinati

A common musical device in many sorts of music is the ostinato: a rhythmic motive that repeats within a context that is not similarly repeating. If the length of the ostinato does not align with the prevailing meter, the ostinato can create a sense of grouping dissonance. In these cases, the rhythms on their own may not indicate a grouping dissonance, but combined with the pitch content of the ostinato, a grouping dissonance becomes audible.

Igor Stravinsky, a particular lover of metrical dissonance and other kinds of rhythmic surprise, creates grouping dissonance with an ostinato in the “Alleluia, laudate dominum” from Symphony of Psalms (Example 9). While the half notes that form the bass line of this excerpt are not themselves in conflict with the [latex]\mathbf{^3_2}[/latex] meter, the repeating pattern of four notes (E♭–B♭–F–B♭) suggests a four-beat grouping that does not align with the three-beat grouping of the melody and other lines. Listen to the example twice: the first time, conduct the [latex]\mathbf{^3_2}[/latex] meter of the melody; the second, conduct [latex]\mathbf{^4_2}[/latex] with the bass line.

Example 9. A 4-layer in the ostinato creates a grouping dissonance with the 3-layer in the other voices in Stravinsky’s “Alleluia, laudate dominum” from Symphony of Psalms (6:37).

Changing Dissonance

Some music gets into a groove and sticks with it, but many do not: a piece may use metrical dissonance in some places and not others, creating a sense of tension-and-release. Consider the Bill Withers example above: the metrical dissonance in the B section contrasts with the A section that rhythmically very straight and without dissonance.

Let’s close with an example of this technique of changing dissonance in Brahms well-known “Lullaby” (“Wiegenlied”, Op. 49, No. 4).^[4] The rhythm of the vocal melody is highly regular in the notated [latex]\mathbf{^3_4}[/latex]. Now have a look at the piano accompaniment, shown in Example 10. The left hand (bass) is every bit as regular as the voice, but the right hand (treble) goes its own way:

1. 1. We start with a rhythmic pattern suggesting three-eighth-note-long groupings that might fit better in [latex]\mathbf{^6_8}[/latex] rather than [latex]\mathbf{^3_4}[/latex], displaced by an eighth. (So before the voice even enters we arguably have both displacement and grouping dissonance!)
   2. The grouping dissonance disappears almost immediately and shifts to displacement dissonance: we settle on a two eighth note grouping structure, but displacement by an eighth. This remains for the majority of the verse.
   3. The opening double-dissonance briefly returns, before giving way to…
   4. …the right hand (finally) playing a note on the downbeat! The dotted-quarter on beat 2 may still suggests displacement dissonance, but of a milder kind: displacement forward by a quarter note, to emphasize the second beat instead of the first (like a sarabande).
   5. Finally, a measure later, we have all 6 eighth notes in the bar in a strong-weak alternation—no sense of dissonance at all.
   6. The last four-bar pattern repeats.

This reading (which you may, of course, disagree with) describes a process of (slight) tension to release that is entirely in keeping with the mood of this lullaby.

Example 10. Changing metrical dissonance in Brahms’ “Lullaby” (“Wiegenlied”, Op. 49, No. 4).

1. Grouping Dissonance Composition Exercise (.pdf, .mscz). Asks students to compose two mini pieces with repeating motives of different lengths, creating grouping dissonance. References the pentatonic and hexatonic collections.