VIII. 20th- and 21st-Century Techniques
Intervals in Integer Notation
Megan Lavengood and Brian Moseley
Key Takeaways
- When analyzing atonal music, intervals may be better understood as a number of semitones, rather than using tonal interval names.
- There are four types of interval:
- Ordered pitch intervals measure the number of semitones between pitches, and indicate direction with a plus or minus sign (+/−).
- Unordered pitch intervals measure the number of semitones between pitches, but do not indicate direction (no +/−).
- Ordered pitch class intervals measure the distance between two pitches in pitch class space (the clock face), always moving clockwise (ascending). This is similar to measuring time on a 12-hour clock: 9–5 is 8 hours, never 4.
- Interval classes (unordered pitch class intervals) represent the smallest possible distance in semitones between two pitch classes; therefore, an interval class is always ≤6.
- Ordered pitch intervals are as specific as possible: they measure specific pitches (in specific octaves) and represent the directionality of the interval.
- Interval classes are the most abstract type of interval: they represent the smallest possible distance between two pitch classes.
In tonal music, because intervals are dependent upon the pitches that create them, the consonance and dissonance of intervals is determined by tonality itself. Imagine the interval created by G and B♭, a minor third. In the context of G minor, this is a consonant interval. Respelled as G and A♯, perhaps in the context of B minor, it creates a dissonant augmented second. From a tonal perspective, then, the two intervals are different in these different tonal contexts, even though they are the same keys on a piano keyboard (Example 1).
Example 1. Even though B♭ and A♯ are the same key on the keyboard, the intervals of a minor third and an augmented second are distinct in tonal theory.
Contrast this with atonal music. Because atonal music has no tonality, the distinction between B♭ and A♯ no longer matters. In this context, the intervals G–B♭ and G–A♯ are the same. For this reason, we will not use tonal interval names like “minor third.” Instead, we will measure the intervals by the number of semitones between the pitches or pitch classes.
We can describe intervals according to two types of information: pitches vs. pitch classes, and ordered vs. unordered intervals. Combined, this makes four types of intervals, summarized in Example 2. Each of these interval types is explained below.
| pitch intervals | pitch-class intervals | |
|---|---|---|
| ordered intervals | ordered pitch intervals | ordered pitch-class intervals |
| unordered intervals | unordered pitch intervals | unordered pitch-class intervals / interval classes (IC) |
Example 2. Four interval types in atonal theory.
Pitch Intervals (ordered and unordered)

Pitch intervals are the distance between pitches as measured in semitones, which is to say that octave is taken into consideration. Thus, the interval C4–E4 is 4: four semitones are between these notes. But if that E is moved up an octave (C4–E5), the interval becomes 16: four semitones between C and E, plus an octave (twelve semitones) between the lower E and the higher E.
Within pitch intervals, there are ordered and unordered variants. To create an ordered pitch interval, simply add a plus or minus sign to indicate whether the interval is ascending or descending. Unordered pitch intervals, by contrast, do not indicate which direction the pitches move in—they are thus more suitable for harmonic intervals. The differences between ordered and unordered pitch intervals are summarized in Example 3.
Ordered Pitch-Class Intervals
Pitch-class intervals are the distance between pitch classes as measured in semitones in pitch class space—that is, around the clock face. Returning to our C4–E5 interval, we are now interested just in the pitch classes C and E, without reference to a specific octave.
Ordered pitch-class intervals measure the distance between pitch classes, always ascending. This is visualized most easily by picturing the twelve tones around a clock face, then measuring the interval by going around the circle clockwise. Thus, from C to E = 4, but E to C = 8 (Example 4). In everyday life, this is similar to measuring time on a twelve-hour clock, or calculating the duration of a shift at work: if you arrive at work at 9:00 am and work until 5:00 pm, that’s 8 hours; the ordered pitch class interval from A (pc 9) to F (pc 5) is also 8.
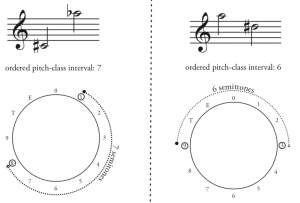
Interval Classes (IC)
Unordered pitch-class intervals are usually called interval classes. Interval class is the smallest possible distance between two pitch classes. On the clock face, this means traveling either clockwise or counter-clockwise, whichever is shortest. Interval class is a useful concept because it relates intervals, their inversions, and any compound versions of those intervals. You should be able to connect this concept to the concept of pitch vs. pitch class: a pitch class is a pitch, its enharmonic respelling(s), and any octave displacements of those spellings.
This means that there are only six interval classes: 1, 2, 3, 4, 5, and 6. If you reach the pitch class interval of 7, it becomes shorter to move counter-clockwise, and 7 becomes 5. For the same reason, 8 becomes 4, 9 becomes 3, and so on. Both C–E and E–C are interval class 4 (Example 5).
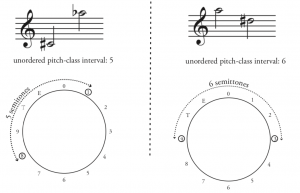
Summary
Using various combinations of pitch interval, pitch-class interval, ordered, and unordered, we arrive at four different conceptions of interval.To wrap your mind around each of these and begin to understand their various analytical uses, think of them on a sliding scale of most concrete (the ordered pitch interval) to most abstract (the unordered pitch-class interval). You can find this related to other concepts in the Set Theory Quick Reference Sheet.
In tonal music, it’s useful to distinguish between a thirteenth and a sixth in some situations, but not others. In the same way, as you analyze atonal music, you will find that different types of intervals are useful for describing different types of phenomena.
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Intervals (.pdf, .docx). Asks students to identify interval types (integer notation) within pieces of music. Worksheet playlist
Media Attributions
- Ordered vs unordered pitch interval © Bryn Hughes adapted by Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Ordered pitch class intervals © Bryn Hughes adapted by Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Pitch classes © Bryn Hughes adapted by Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
An adjective describing music that lacks any sense of tonal center.
One-twelfth of an octave; generally considered to be the smallest interval in Western musical notation.
The distance between two pitches measured in semitones, with a plus or minus symbol to indicate ascending or descending, respectively. For example: C₄ to E₅ would be an ordered pitch interval of +16.
The distance between two pitches, measured in semitones. For example, C₄ to E₅ would be an unordered pitch interval of 16.
The distance between pitch classes from lowest to highest. In other words, pitch class intervals are measured on the clock face, always going clockwise.
Unordered pitch-class intervals; that is, the smallest possible distance in semitones between two pitch classes. Thus, mi2 and ma7 are both IC 1; ma2, mi7, +6 are IC 2; mi3, ma6, +2 are IC 3, etc. The largest interval class is six semitones, because if order is disregarded, the tritone is the largest possible interval.
An adjective used to describe music that adheres to the Western system of functional harmony.
A discrete tone with an individual frequency.
A group of pitches that are octave equivalent and enharmonically equivalent.

