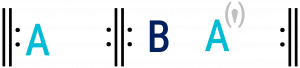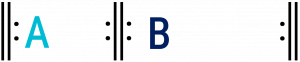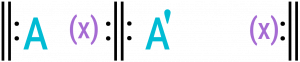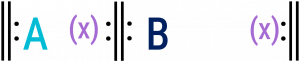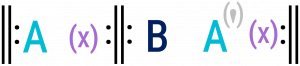Chapter Playlist

In the context of musical form, the term “binary” refers to a formal type that has two main parts. These parts are often called reprises because each is typically repeated. Binary forms are common in 17^th-, 18^th-, and 19^th-century repertoire, and they were used heavily in dance music.

There are two types of binary form: rounded and simple. Both forms have the possibility of featuring a balanced aspect as well (note: balanced binary is often described as its own type of binary form, but that approach is not taken here).

Binary form is typically one of the shorter forms, and because of that, it is often embedded within larger, compound forms like compound ternary form.

Repeat Structure and Types of Binary Form

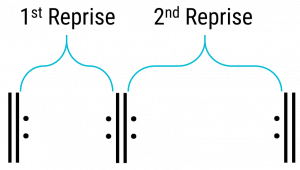
Example 1. Abstract diagram of the repeat structure in binary form.

In 17^th– and 18^th-century classical music, each reprise of the binary form is typically repeated, as in Example 1. The listener will hear the following structure:

• Reprise 1
• Reprise 1
• Reprise 2
• Reprise 2

In 17^th– and 18^th-century music, it is very common to find the repeat signs written in the score. Decorative improvisation on the repeat was expected without being specified in the score. But in the 19th century, it became more common for composers to write out the repeat instead of using repeat signs. This may be done to indicate specific decorations on the repeat, to include changes in some musical domain (like instrumentation or register), and/or to expand the music beyond the length of its first statement.

While having two—usually repeated—reprises is common to all binary forms, there are two relatively distinct sub-types that capture the form’s larger melodic organization: rounded and simple, shown in Example 2. Formal organization is represented with uppercase letters and prime symbols.

The first section of a binary form piece is represented with the letter A. In both subtypes of binary form, A is the main section and presents the main melodic material (see Formal Sections in General).

B sections (the contrasting sections) vary depending on the type of binary form (Example 2). Both forms can also feature a balanced aspect (represented with an x in parentheses), as discussed further below.

Example 2. Abstract diagram of each binary form.

Rounded Binary Form

Example 3. Abstract diagram of rounded binary form.

In rounded binary, the beginning of A returns in the home key somewhere in the middle of the second reprise. It is not necessary for all of A to return (though often it does)—only the beginning. While the returning material may be exactly the same, it’s also common to see slight variations, like change of octave, accompanimental pattern, and/or melodic embellishments. If there is variation, you should still be able to experience the feeling of return when the A material comes back. If unsure, you can expect the harmonic analysis to remain essentially the same, the chord changes will likely be in the same metric locations, and the scale degrees of the melody will also be in the same order and in the same metric locations; just make sure to account for the possibility of slight variation in the domains listed above.

In rounded binary form, the second reprise starts with a B section. Typically, the B section is less stable than the A section and may involve common destabilizing features like sequences, chromaticism, and dominant pedals. In some binary forms, however, the B section is quite stable but simply presents different thematic material than A (see, for example, the B section of the Trio from the third movement of Mozart’s String Quartet in G major, K. 80).

Rounded Binary Example

The Menuetto from the third movement of Mozart’s Symphony no. 25 in G minor (Example 4) is a clear instance of a rounded binary form typical of the mid- to late 18^th century. After a relatively stable thematic statement during the first reprise (mm. 1–12, A), the second reprise (mm. 13–36) can easily be divided into two distinct parts, B (mm. 13–20) and A′ (mm. 21–36). The impression of a division is the result of the return of A material at m. 21 and the half cadence that precedes it at m. 20.

In the 18^th century, half cadences before the return of A in rounded binary forms are quite common. In the 19^th century, however, composers may also elide or otherwise obscure this boundary, as Chopin does between mm. 16 and 17 in the rounded binary form found in mm. 1–24 of his polonaise in A major, Op. 40, no. 1.

Example 4. Mozart, Symphony no. 25 in G minor, 3^rd movement, Menuetto.

Simple Binary Form

In simple binary, there is no substantial return of opening material in the second reprise. Instead, the material in the second reprise takes one of two possible manifestations:

1. A′ (note the prime symbol): The second reprise, though not a repeat of the first reprise, continues with the same sorts of ideas. As the A material is always present, there is no “return” to the opening material.
2. B: The second reprise contains relatively new material throughout.

or

Example 5. Abstract diagrams of simple binary form.

Simple Binary Example

The Bourrée from Bach’s Lute Suite in E minor, BWV 996 (Example 6) is a good example of a simple binary form where the second reprise would be labeled A′. The musical material in the second reprise simply continues the ideas from the first reprise throughout. Notice how there is no clear return of the first reprise’s opening material in the middle of the second reprise, and therefore, this is not an example of rounded binary.

Example 6. J. S. Bach, Bourrée from Lute Suite in E minor, BWV 996.

Balancing a Binary Form

“Balanced” is a term used to describe a binary form (either simple or rounded) in which the tail end of the first reprise returns at the tail end of the second reprise. That return will be in the piece’s home key, even if it was in another key in the first reprise. In Example 7, the (x) represents the music at the tail end of the first reprise (A section) and its return at the tail end of the second reprise.

In order to be considered a return, there needs to be a crux point—a particular moment where the restatement begins at the tail end of the second reprise. This restatement is the point at which there is a direct bar-for-bar mapping of measures between the tail ends of both reprises. Importantly, this excludes rounded binary examples where the entire first reprise is repeated verbatim in the second reprise, because there is no crux point at the tail end of the second reprise.

or

or

Example 7. Abstract diagrams of each binary form with balanced aspect.

Simple Binary (Balanced) Example

In longer simple binary forms, the balancing material can be quite substantial. In Domenico Scarlatti’s Sonata in A major, K. 322 (Example 8), the material that returns is nearly 24 measures long—over half the length of the first reprise—and is easily recognizable by ear. In the Scarlatti work, (x) starts in the middle of m. 21 and ends at the end of the first reprise, m. 44. That material returns in the second reprise in the middle of m. 59 and continues to the end of the work, with a few new melodic decorations along the way (compare m. 26 and m. 63, for example). Importantly, note that (x) in the second reprise has been transposed back to the home key. In other words, when it was stated initially in the first reprise, (x) was in the key of E minor/E major, so it needed to be transposed back to the key of A in order for the work to start and end in the same key.

Example 8. Domenico Scarlatti, Sonata in A major, K. 322. Click to download a PDF score.

Harmonic Expectations

Cadences

Each part of the binary form commonly ends with standard cadence types (perfect authentic, imperfect authentic, or half), especially in 18^th-century classical music. But stylistic preferences of the 19^th century alter cadential expectations for the first part in particular: composers sometimes opted for lower levels of closure, ending with tonic-prolongational progressions instead of standard cadence types (examples:  Schumann, Papillon, 1 [m. 8] & 7 [m. 8], Kinderszenen, no. 9 [m. 8]).

Harmonically Open or Closed

As with other forms, the first reprise of a binary form can be described as harmonically open or closed. The second reprise can be described this way as well, but because binary forms are expected to be monotonal, it usually is implied instead.

Keys

If the first reprise of a binary form is open, it may contain a modulation.

Regardless of the harmonic situation at the end of the first reprise, you should expect the second reprise to end with an authentic cadence in the original key. There may be additional cadences before the end, but the PAC at the end of the second reprise is essentially an obligatory convention in common-practice-period tonal music. If a piece starts and ends in different keys, it exhibits progressive tonality rather than monotonality.

Beginning, Middle, End – Stability Expectations

As with most aspects of form, binary form moves between relative stability and relative instability throughout the form which serves to give the work a linear drive due to the expectation that a work will start stable, become unstable, and ultimately end with a sense of relative stability. In binary form, you can expect that:

• The first reprise is relatively stable.
• The beginning of the second reprise is relatively unstable. This is so common that some theorists refer to the second reprise as a “digression” or “departure,”^[1] sometimes forgoing the letter B altogether to focus on the function of the music.
• The end of the second reprise returns to stability. The return of A material in the second reprise of a rounded binary form is also commonly expected to be a point of relative stability.

1. Binary Form Analysis Assignment (.pdf, .docx)
   • Audio Example 1 – Franz Schubert, Écossaise, D. 529, No. 3 (Starts at 1:07)
   • Audio Example 2 – Franz Joseph Haydn, Piano Sonata no. 37, III, theme
   • Audio Example 3 – Johann Sebastian Bach, Sarabande from Violin Partita no. 1, BWV 1002
   • Audio Example 4 – Franz Schubert (1797-1828), Piano Sonata in E major, D. 157, II (mm. 1– 16)
   • Audio Example 5 – Franz Schubert (1797-1828), Symphony no. 2 in B♭ major, D. 125, II
2. Guided Composition (.pdf, .mscz)