VIII. 20th- and 21st-Century Techniques
Pitch and Pitch Class
Megan Lavengood
Key Takeaways
- Set theory often relies on the distinction between pitch versus pitch class.
- Pitch classes are best represented with integer notation, where C=0.
Pitch
Pitches are discrete tones with individual frequencies.
The concept of pitch, then, does not imply octave equivalence. C4 is a pitch, and it is not the same pitch as C3.
Pitch Class
Throughout set theory, the word “class” means “group.” So a pitch class is a group of pitches—all pitches related by octave equivalence and enharmonic equivalence. You have probably encountered both of these concepts before, even if not by name.
Our system of letter names for notes implies octave equivalence: equivalence between pitches that are spelled the same but are any number of octaves apart. C4 is the same as C3 is the same as C9, and so on, because they are all Cs (Example 1).
When someone says “there are twelve notes,” they are implying enharmonic equivalence. Two notes are enharmonically equivalent if you would press the same key on the piano to play them—even if the spelling is different. Enharmonic equivalence is the sense in which A♭ and G♯ are “the same.” While tonal music nearly always distinguishes between enharmonic pitches—A♭ as le [latex](\downarrow\hat{6})[/latex] leads to G, but G♯ as si [latex](\uparrow\hat{5})[/latex] leads to A—post-tonal music is often different.[1] Because many composers no longer felt constrained by a tonal center, the relationships among scale degrees and spellings aren’t important.
In summary, pitch classes are groups of pitches related by octave and enharmonic equivalence. A♭4, A♭3, G♯2, etc. are all members of the same pitch class.
Example 1. Pitch versus pitch class.
Integer Notation
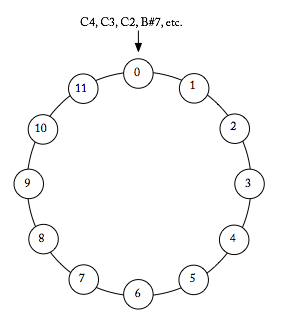
If notes are enharmonically equivalent, then the system of seven letter names does not work well to describe the twelve pitch classes. Instead, in set theory, we use integer notation, which assigns a number between 0 and 11 to each pitch class (Example 2). All Cs, and any notes that are enharmonically equivalent to C (B♯, for example), are pitch class 0. All C♯s, and any notes that are enharmonically equivalent to C♯ (D♭, for example) are pitch class 1, and so on. To summarize with a few of the most common note names:
- C (B♯, etc.)
- C♯, D♭
- D (C𝄪, etc.)
- D♯, E♭
- E (F♭, etc.)
- F (E♯, etc.)
- F♯, G♭
- G (F𝄪, etc.)
- G♯, A♭
- A (G𝄪, etc.)
- A♯, B♭
- B (C♭, etc.)
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Pitch and pitch class (.pdf, .mscz). Asks students to translate between pitch class integers, note names, and staff notation.
Media Attributions
- Pitch Space © Bryn Hughes is licensed under a CC BY-SA (Attribution ShareAlike) license
- Pitch-class-Space © Bryn Hughes is licensed under a CC BY-SA (Attribution ShareAlike) license
- Post-tonal music is extremely various. Composers have individual compositional styles, aesthetic goals, and unique conceptions of pitch. All this is to say that you must approach a composition with flexibility. For example: because it is quasi-tonal, Debussy’s music often benefits from a view that does not assume enharmonic equivalence. But sometimes it does. You must rely on your musical intuitions when analyzing this music, and you should also be willing to approach pitch in these compositions from multiple perspectives until you find one that seems most appropriate. ↵
A methodology for analyzing pitch in atonal music. Pitch classes are given an integer name (0–11, where C is 0, C♯ is 1, etc.). Groups of pitches are considered together as "sets." Sets may be related by inversion or transposition.
A discrete tone with an individual frequency.
A group of pitches that are octave equivalent and enharmonically equivalent.
A system of naming pitch classes that treats C as 0, C♯ as 1, D as 2, etc.
A relationship between pitches that share a letter name but are separated by one or more octaves.
A relationship between notes, intervals, or chords that sound the same but are spelled differently.


