In second-species counterpoint, the counterpoint line moves in half notes against a cantus firmus in whole notes. This 2:1 rhythmic ratio leads to two new “fundamental musical problems”—one metric and one harmonic: the differentiation between strong beats and weak beats, and the introduction of the passing-tone dissonance. The introduction of harmonic dissonance into second species adds to the variety of the musical texture. However, it brings a tension that must be balanced with consonance to promote tonal fusion, and it requires careful attention in order to maintain smoothness in and out of the dissonance.

Here are the complete examples of second-species counterpoint from Part I of Gradus ad Parnassum, annotated (as before) with the interval that the counterpoint line makes with the cantus firmus. For the complete examples from Gradus ad Parnassum as exercises, solutions, and annotations, see Gradus ad Parnassum Exercises.

Example 1. All second-species exercises from Gradus ad Parnassum.

The Counterpoint Line

As in first species, the counterpoint line should be singable and have a good shape, with a single climax and primarily stepwise motion (with some small leaps and an occasional large leap for variety). However, because a first-species counterpoint had so few notes, in order to maintain smoothness in other aspects of the exercise, the melody frequently employed small leaps. In second species, the increase in notes and the added freedom involving the use of dissonance makes it easier to move by step without causing other musical problems. Thus, a second-species counterpoint is even more dominated by stepwise motion than in first species. If the counterpoint must leap, take advantage of the metrical arrangement to diminish the attention drawn to the leap: leap from strong beat to weak beat (within the bar) rather than from weak beat to strong beat (across the bar line) when possible. Also, because there are more notes in a second-species line, there should usually be one or two secondary climaxes—notes lower than the overall climax that serve as “local” climaxes for portions of the line. This will help the integrity of the line by ensuring that it has a coherent shape and does not simply wander around.

Beginning and Ending

Beginning a second-species counterpoint

As in first species, begin a second-species counterpoint above the cantus firmus with do [latex](\hat1)[/latex] or sol [latex](\hat5)[/latex]. Begin a second-species counterpoint below the cantus firmus with do [latex](\hat1)[/latex].

A second-species line can begin with two half notes in the first bar, or a half rest followed by a half note. Beginning with a half rest establishes the rhythmic profile more readily, making it easier for the listener to parse, so it is often preferable. It is also easier to compose. Regardless of rhythm, the first pitch in the counterpoint should follow the intervallic rules above.

Ending a second-species counterpoint

As in first species, you should end with a clausula vera: the final pitch of the counterpoint should be do [latex](\hat1)[/latex]; the penultimate note of the counterpoint should be ti [latex](\hat7)[/latex] if the cantus is re [latex](\hat2)[/latex], and re [latex](\hat2)[/latex] if the cantus is ti [latex](\hat7)[/latex].

The penultimate bar of the counterpoint can either be a whole note (making the last two bars identical to first species) or two half notes. This allows you to begin your clausula vera on either the strong beat or the weak beat of the penultimate measure.

Strong Beats

The inclusion of dissonance in a musical texture creates new musical problems that need to be addressed. Because the philosophy of species counterpoint is to present only a small number of new musical difficulties with each successive species, second-species counterpoint introduces dissonance in a very limited way.

Strong beats (downbeats) in second species are always consonant. As in first species, prefer imperfect consonances (thirds and sixths) to perfect consonances (fifths and octaves), and avoid unisons.

Because motion across bar lines (from weak beat to strong beat) involves the same kind of voice motion as first species (two voices moving simultaneously), follow the same principles as first-species counterpoint. For instance, if a weak beat is a perfect fifth, the following downbeat cannot also be a perfect fifth.

Likewise, progressions from downbeat to downbeat must follow the principles of first-species counterpoint described in the previous chapter, such as:

• Do not begin two consecutive bars with the same perfect interval.
• Do not outline a dissonant melodic interval between consecutive downbeats. (Exception: if the counterpoint leaps an octave from the strong beat to the weak beat, the leap should be followed by step in the opposite direction, making a seventh with the preceding downbeat. This is okay, since it is the result of smooth voice motion.)
• Do not begin more than three bars in a row with the same imperfect consonance.

Hidden or direct fifths/octaves between successive downbeats are fine, as the effect is weak, and diminished by the intervening note in the counterpoint.

Weak Beats

Since harmonic dissonances can appear on weak beats, a mixture of consonant and dissonant intervals on weak beats is the best way to promote variety.

Unisons were problematic in first species because they diminished the independence of the lines. However, when they occur on the weak beats of second species and are the result of otherwise smooth voice leading, the rhythmic difference in the two lines is sufficient to maintain that independence. Thus, unisons are permitted on weak beats when necessary to make good counterpoint between the lines.

Any weak-beat dissonance must follow the pattern of the dissonant passing tone, explained below. Also explained below are a number of standard patterns for consonant weak beats. Chances are high that if your weak beats do not fit into one of the following patterns, there is a problem with the counterpoint, so use them as a guide both for composing the counterpoint and for evaluating it.

These principles should help guide your use of weak-beat notes in a second-species counterpoint line. A good general practice is to start with a downbeat note, then choose the following downbeat note, and finally choose a pattern below that will allow you to fill in the space between downbeats well.

Most of these principles are used as examples in the demonstration video at the bottom of the page.

Dissonant passing tones (weak beats only)

All dissonant weak beats in second species are dissonant passing tones, so called because the counterpoint line passes from one consonant downbeat to another consonant downbeat by stepwise motion. The melodic interval from downbeat to downbeat in the counterpoint will always be a third, and the passing tone will come in the middle in order to fill that third with passing motion.

Since all dissonances in second species are passing tones, you will not leap into or out of a dissonant tone, change directions on a dissonant tone, nor write a dissonance on a downbeat.

Consonant weak beats

Unlike dissonant weak beats (of which there is only one type), there are several types of consonant weak beats available (Example 2):^[1]

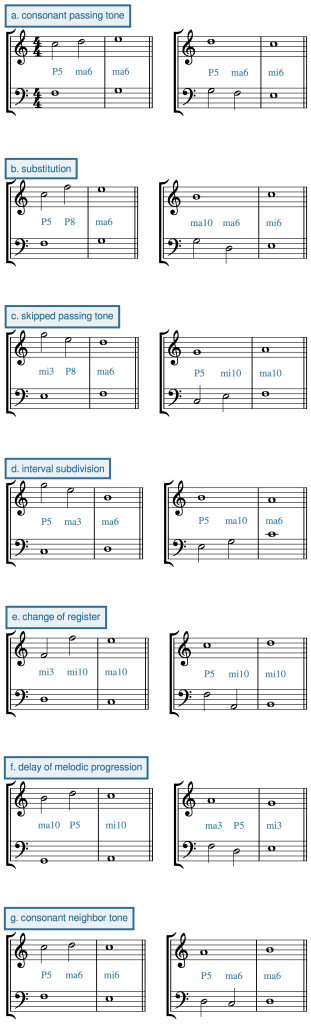
1. 1. A consonant passing tone outlines a third from downbeat to downbeat, and it has the same pattern as the dissonant passing tone, except that all three tones (downbeat, passing tone, downbeat) are consonant with the cantus firmus. A consonant passing tone will always be a sixth or perfect fifth above/below the cantus.
   2. A substitution also outlines a third from downbeat to downbeat. However, instead of filling it in with stepwise motion, the counterpoint leaps a fourth and then steps in the opposite direction. It is called a substitution because it can substitute for a passing tone in a line that needs an extra leap or change of direction to provide variety. Like the consonant passing tone, all three notes in the counterpoint must be consonant with the cantus.
   3. A skipped passing tone outlines a fourth from downbeat to downbeat. The weak-beat note divides that fourth into a third and a step. Again, all three intervals (downbeat, skipped passing tone, downbeat) are consonant with the cantus.
   4. An interval subdivision outlines a fifth or sixth between successive downbeats. The large, consonant melodic interval between downbeats is divided into two smaller consonant leaps. A melodic fifth between downbeats would be divided into two thirds. A melodic sixth between downbeats would be divided into a third and a fourth, or a fourth and a third. Not only must all three melodic intervals be consonant (both note-to-note intervals and the downbeat-to-downbeat interval), but each note in the counterpoint must be consonant with the cantus.
   5. A change of register occurs when a large, consonant leap (perfect fifth, sixth, or octave) from strong beat to weak beat is followed by a step in the opposite direction. It is used to achieve melodic variety after a long stretch of stepwise motion, to avoid parallels or other problems, or to get out of the way of the cantus to maintain independence. It should be used infrequently. And as always, each note must be consonant with the cantus.
   6. A delay of melodic progression outlines a step from downbeat to downbeat. It involves a leap of a third from strong beat to weak beat, followed by a step in the opposite direction into the following downbeat. It is called a “delay” because it is used to embellish what otherwise is a slower first-species progression (motion by step from downbeat to downbeat).
   7. A consonant neighbor tone occurs when the counterpoint moves by step from downbeat to weak beat, and then returns to the original pitch on the following downbeat. If the first downbeat makes a fifth with the cantus, the consonant neighbor will make a sixth, and vice versa.

Demonstration

Example 3 is a video by Kris Shaffer illustrating the process of composing a second-species counterpoint. This video provides new information about the compositional process, as well as concrete examples of the above rules and principles.

Example 3. Video lesson on composing a second-species counterpoint.

1. Second-Species Counterpoint A (.pdf, .mscx). Asks students to compose a second-species example and do error detection.
2. Second-Species Counterpoint B (.pdf, .mscx). Asks students to compose a second-species example and do error detection.
3. For the complete set of Fux exercises, see the Gradus ad Parnassum chapter.