In the late 19^th century, composers often used triadic progressions that confound conventional Roman numeral analysis. Consider the following excerpt from Brahms’s concerto for violin and cello (Example 1):

A reduction of the chord progression in the excerpt above can be found in Example 2. The passage connects two A♭ major triads; however, the chords in between those triads do not belong to A♭ major in any useful way, nor do they follow any of the conventions of functional harmony.

One might dismiss the passage altogether as “non-functional harmony,” but when you listen to it, it follows a certain kind of logic. As Richard Cohn writes, “if this music [music that is triadic but functionally indeterminate] is not fully coherent according to the principles of diatonic tonality, by what other principles might it cohere?” (1998, 169).

Neo-Riemannian Transformations

Neo-Riemannian theory describes a way of connecting major and minor triads without a tonal context. Example 3 shows the three basic Neo-Riemannian operations. Notice that each operation preserves two common tones in a triad and changes its mode.

• The Relative transformation (R) preserves the major third in the triad and moves the remaining note by whole tone.
• The Parallel transformation (P) preserves the perfect fifth in the triad and moves the remaining note by semitone.
• The Leading-Tone Exchange transformation (L) preserves the minor third in the triad and moves the remaining note by semitone.

It’s important to note that each transformation is a toggle between two chords. As an analogy, think of the caps lock key on your keyboard, which toggles between two cases of letters. If you are typing with lowercase letters and then press caps lock, this tells your keyboard to begin typing in uppercase letters. But if you press caps lock again, it toggles back to lowercase—it doesn’t go to some third case.

Similarly, if you do the L transformation on a C major triad, you get an E minor triad. If you do the L transformation on an E minor triad, you return to a C major triad. Put another way, successive repetitions of the same transformation alternate between two chords, as shown in Example 4.

While most 19^th-century composers didn’t write progressions using the same transformation over and over again, you will find this technique used in twentieth-century works like “O Superman” by Laurie Anderson, which uses successive L transformations throughout.

The Tonnetz

Example 5 shows a Tonnetz. A Tonnetz is a visual representation of pitches arranged such that perfect fifths are read from left to right, major thirds are read diagonally from the top left to the bottom right, and minor thirds are read diagonally from the bottom left to the top right. Any three pitches in a triangle form a major or minor triad. Although it’s pictured here as a flat, confined plane, theoretically, without enharmonic equivalence, the Tonnetz continues on infinitely; with enharmonic equivalence, the Tonnetz forms a torus shape.

Neo-Riemannian transformations can be visualized by flipping a triangle along one of its three edges.

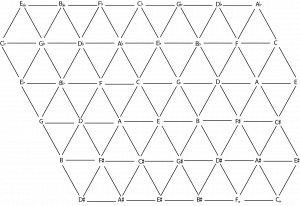
• The (P)arallel transformation flips the triangle along the edge belonging to the line of perfect fifths (left to right).
• The (R)elative transformation flips the triangle along the edge belonging to the line of major thirds (top left to bottom right).
• The (L)eading-tone transformation flips the triangle along the edge belonging to the line of minor thirds (top right to bottom left).

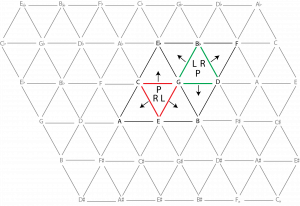
Example 6 shows each of the transformations on the Tonnetz. If you perform a P transformation on the C major triad, highlighted with red edges, it will flip along the C–G side to become C minor. Similarly, L will flip the triad along the G–E edge to become E minor, and R will flip the triad along the C–E edge to become A minor. Note that if you start on a minor triad, such as the G minor triad highlighted with green edges, all of the flips will be in the opposite directions.
Returning to the example from Brahms’s concerto for violin and cello, we now have a means of understanding how this chord progression works. Example 7 shows that the two A♭ major triads are connected by a series of P and L transformations between chords.

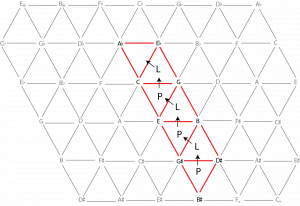
The excerpt from the Brahms concerto navigates a column of triangles moving upward from the bottom right of the Tonnetz, shown in Example 8. Note that you need to enharmonically re-interpret the G♯ major triad as an A♭ major triad at the starting point.

The Tonnetz is useful for visualizing the proximity of major and minor triads; notice that all of the triads in a given key are close together, while tonally disparate keys are also far apart on the Tonnetz. Conversely, the Tonnetz is helpful for imagining interesting chord progressions that you might not think of if you’re limiting yourself to typical common-practice syntax.

Chains or Cycles of Transformations

While you can use Neo-Riemannian theory to create or analyze just about any chord progression, composers have often focused on chains of operations that create closed cycles of triads. Cycles begin and end on the same chord, and they follow a specific pattern of transformations (much like a sequence). The progression from the Brahms example above is a PL cycle because it alternates P and L transformations and begins and ends on the same chord.

There are three possible cycles that use two transformations: the PL cycle, the RP cycle, and the RL cycle. As you can see in Example 9, the PL and RP cycles “close the loop” after relatively few transformations: six for the PL cycle, and eight for the RP cycle.

Conversely, the RL cycle (Example 10) is is quite long: it passes through all 24 major and minor triads. Since this cycle takes so long to “close the loop,” it is often ignored or presented in truncated form.

There is one three-transformation cycle that is noteworthy: the PLR cycle. As Example 11 shows, it takes two cycles of the PLR transformations to return to the starting chord.

Of the cycles mentioned above, both the PL and RP cycles generate a parent scale made up of all of the notes used by its constituent triads. The PL cycle generates the hexatonic scale, a symmetrical scale made up of alternating semitones and minor thirds. The RP cycle generates an octatonic scale, another symmetrical scale made up of alternating semitones and major seconds. You might consider these scales to represent the “overall sound” of the cycle. Each PLR cycle is centered around a single pitch, which is contained in each of the triads within the cycle.

Each of these cycles is illustrated in Example 12.

Other Transformations

There are three other types of Neo-Riemannian transformations that occur frequently enough in the repertoire that they are worth mentioning here.

• The Slide transformation (S) (short for “slide”) is effectively the opposite of the P transformation: it moves the two pitches that form the perfect fifth in a triad by semitone and changes the mode of the triad.^[1]
• The Nebenverwandt transformation (N) moves both members of the minor third in a triad by semitone and again changes the mode. Nebenverwandt means “neighbor-related” in German, and it describes the neighbor-tone-like motion of this third. ^[2]
• The Hexpole (H) transformation connects a triad to its modal opposite a third away by moving each voice by a single semitone, generating the hexatonic poles in the hexatonic PL cycle discussed above and shown in Example 12.^[3]

These three transformations are shown in Example 13.

Of course, all of the above transformations can be considered combinations of the staple P, L, and R transformations. For example, you could describe H as “PLP.” Indeed, you can describe the connection between any two major and/or minor triads as combinations of transformations: you can get from one triad to any other in five steps or less. The most interesting are those that use parsimonious voice leading: voice leading in which no single voice moves more than a step.  There are numerous other combinations you could come up with—try some on your own!

More Networks of Neo-Riemannian Transformations

Augmented triads

Although it is not part of the staple Neo-Riemannian transformations, which only deal with major and minor triads, the augmented triad provides a useful link between major and minor triads, specifically those that are connected by R transformations. Upon scrutinizing the above examples, you may have noticed that the R transformation isn’t quite the same as the P and L transformations, because it moves its non-preserved note by two semitones, while the others move their non-preserved note by one semitone. In a sense, the R transformation is twice as much “work” as the P and L transformations. If we fill in the gap between two R-related triads, an augmented triad emerges, as shown in Example 14.

Things get interesting when you consider the augmented triad’s ambiguity. Because it is a symmetrical chord (like the diminished seventh chord), you can enharmonically respell the augmented triad such that any of its chord members can act as the root. For example, the C augmented triad in Example 14 could also be spelled as an E augmented triad (E–G♯–B♯), or an A♭ augmented triad (A♭–C–E). As a result, you can resolve the augmented triad to three different minor triads by moving a single voice by semitone, depending on how its root is interpreted. Example 15 shows the three possible resolutions of the C⁺ triad.

Likewise, the same augmented triad can connect to three different major triads by moving a single voice by semitone, as shown in Example 16.

Example 17 illustrates the four augmented triads (yes, there are only four, due to the symmetry of the chord) and the major and minor triads they can resolve to by moving only one voice by semitone. Each augmented triad and its six associated triads are referred to as Weitzmann regions, named after the theorist Carl Friedrich Weitzmann, who wrote at length about the augmented triad and its versatility in several 19^th-century treatises.
Each line in a Weitzmann region represents moving one note in a triad by a single semitone. When you trace a path from a triad on the left to a triad on the right, you’ll find several of the transformations discussed previously. R, S, and N each require a total move of two semitones, and each of these can be traced through any given Weitzmann region.

The Cube Dance

Recall that the LP, RP, and PLR cycles are “closed loops.” These recurring patterns are interesting, but could grow stale after a while. What if there were a way to “modulate” between cycles? Enter the augmented triad.

Take another look at the major triads connected to the C⁺ Weitzmann region: C, E, and A♭. Notice that these three major triads are the same as those found in the PL cycle that started on C, found in Example 12. The minor triads in that PL cycle can be found in a different Weitzmann region: the E♭⁺ region. If we add augmented triads into our PL cycles, we grow the group of possible chords within a cycle from six to eight. Instead of representing these cycles on a hexagon, let’s illustrate them using a cube, as shown in Example 18.

The PL cycle that starts on C can be found in the top right of Example 18. Each side of the cube represents the motion of one note in the triad moving by semitone. When the triads move from major to minor, these are either P or L transformations. The augmented triads that connect to the major and minor triads are on opposite corners of the cube, and, of course, these connect to each adjoining triad by a one-semitone move as well.

Now, how might we “modulate” from one PL cycle to another? Notice that the same augmented triad can be found in two different cubes. If we wrote a chord progression within one PL cycle, we could “jump” to an adjacent PL cycle by navigating to one of the two augmented triads and continue in the new cycle. In a sense, each cube is connected to two other cubes via an augmented triad. We can use these connections to create a single illustration that provides us a map of all major and minor triads connected by a single semitone. This was first explained by Jack Douthett and Peter Steinbach (1998), who referred to this diagram as a “cube dance.” The cube dance has been reproduced in Example 19.

Using the cube dance model, you could create a chord progression starting in the PL cycle that includes C, and modulate to a new PL cycle via either the C⁺ or E♭⁺ triads. If you wanted to get from C to, say, D, you would have to modulate twice: either through C⁺ and D♭⁺, or E♭⁺ and D⁺. Though the other cycles are not depicted clearly on the cube dance model, you can also use augmented triads to modulate between RP cycles, or PLR cycles, or indeed any group of Neo-Riemannian transformations that include R transformations.

Perhaps even better than the Tonnetz, the cube dance illustrates the proximity of major and minor triads. If we equate proximity with the total number of semitones needed to move from one triad to another, the cube dance diagram puts chords together that we would intuitively consider to be “close” to one another, while those that we might consider “distant” are relatively far apart. Moreover, the cube dance (and even the Tonnetz) does this without reference to a tonal center, making it useful for rationalizing chord progressions from music of the 19^th and 20^th (and even 21^st) centuries that is triadic but shies away from functional tonality. This can be incredibly helpful when analyzing this kind of music, or even when writing your own.

• Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1 (March): 9–40.
• Cohn, Richard. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations.” Journal of Music Theory 41, no. 1 (Spring): 1–66.
• Cohn, Richard. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective.” Journal of Music Theory 42, no. 2 (Autumn): 167–80.
• Cohn, Richard. 1998. “Square Dances with Cubes.” Journal of Music Theory 42, no. 2 (Autumn): 283–96.
• Cohn, Richard. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57, no. 2 (Summer): 285–323.
• Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2 (Autumn): 241–63.
• Engebretsen, Nora, and Per F. Broman. 2007. “Transformational Theory in the Undergraduate Curriculum – A Case for Teaching the Neo-Riemannian Approach.” Journal of Music Theory Pedagogy 21:39–69.
• Jarvis, Brian Edward. “Tonnetz Master.” https://brianedwardjarvis.com/MusicTheoryWebApps/tonnetz_master/tonnetz_master.html
• Mason, Laura Felicity. 2013. “Essential Neo-Riemannian Theory for Today’s Musician.” Master’s thesis, University of Tennessee, Knoxville. https://trace.tennessee.edu/utk_gradthes/1646.

1. Worksheet on Neo-Riemannian Transformations (.pdf, .mscz). Asks students to perform P, L, R, SLIDE, N, and H on individual triads, to realize chains of transformations, and find a transformation chain to connect two chords.
2. Composing with Neo-Riemannian Transformations (.pdf, .mscz). Asks students to use the Cube Dance and other Neo-Riemannian cycles to compose a short minimalist piano solo.