I. Fundamentals
Intervals
Chelsey Hamm and Bryn Hughes
Key Takeaways
- Two pitches form an interval, which is usually defined as the distance between two notes.
- Melodic intervals are played or sung separately, while harmonic intervals are played or sung together.
- Every interval has a size and a quality. An interval’s size is the distance between two notes on a staff—i.e., it is a measurement of the number of lines and spaces between two notes.
- Interval size is considered generic. In other words, it doesn’t matter what accidentals you apply to the notes, the size is always the same.
- A quality makes an interval specific when used in combination with a size. Unisons, fourths, fifths, and octaves form perfect intervals, while seconds, thirds, sixths, and sevenths form major and minor intervals.
- Any interval can be augmented or diminished. Augmented intervals are one half step larger than a perfect or major interval. Diminished intervals are one half step smaller than a perfect or minor interval.
- Intervals between a unison and an octave are called simple intervals. Any interval larger than an octave is a compound interval.
- Intervallic inversion occurs when two notes are “flipped.” When you need to identify an interval where the lower note is the tonic of a difficult or imaginary major key, inverting the interval can help.
- Consonant intervals are intervals that are considered more stable, as if they do not need to resolve, while dissonant intervals are considered less stable, as if they do need to resolve.
Two pitches form an interval, which is usually defined as the distance between two notes. But what does an interval measure? Physical distance on the staff? Difference in wavelength between pitches? Something else? Music theorists have had contradictory ideas on the definition of “interval,” and these definitions have varied greatly with milieu. This chapter will focus on intervals as a measure of two things: written distance between two notes on a staff, and an aural “distance” (or space) between two sounding pitches. It will be important to keep in mind at all times that intervals are both written and aural, so that you are thinking of them musically (and not simply as an abstract concept that you are writing and reading).
Size
Intervals can be melodic (played or sung separately) or harmonic (played or sung together). In Example 1, the notes in the first measure sound together (harmonically), while in the second measure, they sound separately (melodically).
Example 1. A harmonic and a melodic interval.
Every interval has a size and a quality. A size is the distance between two notes on a staff—i.e., it is a measurement of the number of lines and spaces between two notes. Sizes are written with Arabic numbers (2, 3, 4, etc.); however, they are spoken with ordinal numbers (second, third, fourth, fifth, sixth, seventh, etc.). Always begin with “one” when counting size. Example 2 shows the eight sizes within a C major scale. As you can see, the sizes are labeled with ordinal numbers, with two exceptions: the interval between two notes on the same line or space is called a “unison,” not a “first,” and notes eight lines and spaces apart are said to be an “octave,” not an “eighth.”
Example 2. Sizes of intervals.
Size is considered generic. In other words, it doesn’t matter what accidentals you apply to the notes—the size is always the same. Example 3 demonstrates this: despite the different accidentals, each of these intervals is a third (or “generic third”) because there are three lines/spaces between the two notes.
Example 3. Accidentals do not affect an interval’s generic size.
You can practice identifying interval size with the following exercise:
Perfect, Major, and Minor Qualities
A quality makes an interval specific when used in combination with a size. Quality more precisely measures written distance between notes, and—in combination with an interval’s size—it describes the aural sound of an interval.
There are five possible interval qualities:
- Augmented (designated as A or +)
- Major (ma)
- Perfect (P)
- Minor (mi)
- Diminished (d or o)
The quality comes before the size when saying or writing an interval. For example, an interval could be described as a “perfect fourth” (abbreviated P4), a “minor third” (abbreviated mi3), or an “augmented second” (abbreviated A2 or +2).
For now, we will only discuss three qualities: perfect, major, and minor. Different theorists (in different locations and time periods) have applied these qualities to different sizes of intervals, depending on milieu. Example 4 shows how these qualities are applied today. The left column shows that seconds, thirds, sixths, and sevenths are major and/or minor, while the right column shows that unisons, fourths, fifths, and octaves are perfect intervals.
| Major/Minor | Perfect |
|---|---|
| 2nds | Unisons |
| 3rds | 4ths |
| 6ths | 5ths |
| 7ths | Octaves |
Example 4. Interval qualities.
The “Major Scale” Method for Determining Quality
There are several different methods for learning to write and identify qualities of intervals. One method you may have heard of is counting half steps. We do not recommend this method, because it is time consuming and often inaccurate. Instead, we recommend using what you know about major scales to identify interval quality.
To identify an interval (size and quality) using this method, complete the following steps:
- Determine size (by counting lines and spaces between the notes).
- Imagine that the bottom note of the interval is the tonic of a major scale.
- Determine whether or not the top note is in the bottom note’s major scale (imagined in step 2) and assign the corresponding quality.
- If it is: the interval is perfect (if it is a unison, fourth, fifth, or octave) or major (if it is a second, third, sixth, or seventh). If it is not: the interval could be minor (a lowered second, third, sixth, or seventh), or it could be augmented or diminished, which will be covered in the next section.
Example 5 shows two intervals. Try identifying their size and quality:
Example 5. Two intervals.
In Example 5a, the notes are F and C in treble clef. Here is how you would use the “Major Scale” method to identify the interval:
- First, this interval is a generic fifth (F to itself is 1; to G is 2; to A is 3; to B is 4; to C is 5).
- Second, C is within the key of F major (which has one flat, B♭).
- Therefore, the interval is a perfect fifth.
Let’s now use this process for Example 5b. The notes in this example are E♭ and C♭ in treble clef. Let’s go through the same process again:
- First, this interval is a generic sixth (E♭ to itself is 1; to F is 2; to G is 3; to A is 4; to B is 5; to C is 6).
- Second, C♭ is not in the key of E♭ major (which has three flats: B♭, E♭, and A♭).
- Therefore, this is a minor sixth. If it were a major sixth, then the C would have to be C♮ instead of C♭, because C♮ is in the key of E♭ major.
You can practice identifying perfect, major, and minor intervals with the following exercise:
Augmented and Diminished Qualities
To review, there are five possible interval qualities, of which we have covered major, minor, and perfect:
- Augmented (designated as A or +)
- Major (ma)
- Perfect (P)
- Minor (mi)
- Diminished (d or o)
Augmented intervals are one half step larger than a perfect or major interval. The first measure of Example 6a first shows the notes F and C, which form a perfect fifth (because C is in the key of F major). The top note of this interval is then raised by a half step to a C♯, making the interval one half step larger. The interval from F to C♯ is therefore an augmented fifth (abbreviated as either A5 or +5). In the second measure of Example 6a, the first interval is a major sixth between G and E (because E is in the key of G major). The top note is then raised by a half step to E♯, making the interval into an augmented sixth (A6 or +6). The bottom note of an interval can be altered as well. In the first measure of Example 6b, the perfect fifth F–C is turned into an augmented fifth by lowering the F by a half step to F♭, which makes the interval one half step larger than a perfect fifth. In the second measure of Example 6b, the major sixth G–E is turned into an augmented sixth by lowering the G by a half step to G♭.
Example 6. Augmented intervals created by (a) raising the top note and (b) lowering the bottom note.
Diminished intervals are one half step smaller than a perfect or minor interval. In the first measure of Example 7a, the perfect fifth F–C is made a half step smaller by lowering the top note to C♭, forming a diminished fifth (also called a tritone, usually abbreviated as d5 or o5). In the second measure, G–E form a major sixth, which becomes a minor sixth when the top note is lowered by a half step. The minor sixth then becomes a diminished sixth when the top note is lowered again to E𝄫. Note that contracting an interval by one half step turns perfect and minor intervals into diminished intervals, but it turns major intervals into minor intervals. Again, it is not always the top note that is altered. In Example 7b, the perfect fifth F–C becomes diminished when the bottom note moves up a half step to F♯. In the second measure, the major sixth G–E first becomes a minor sixth when the G moves up a half step to G♯. This minor interval then becomes diminished when the G♯ moves to G𝄪 in the third measure, further contracting the interval by another half step.
Example 7. Diminished intervals created by (a) lowering the top note and (b) raising the bottom note.
Example 8 again demonstrates and summarizes the relative size of intervals. Each bracket in this example is one half step larger or smaller than the brackets to its right and left. In Example 8a, the interval quality is changed by altering the top note with accidentals. As you can see, intervals one half step larger than perfect or major intervals are augmented; intervals one half step smaller than major intervals are minor; and intervals one half step smaller than perfect or minor intervals are diminished. Example 8b outlines the same qualities as 10a, only with the bottom note altered by accidentals instead of the top note.
Example 8. Relative size of intervals with (a) the top note altered and (b) the bottom note altered.
You can practice identifying augmented and diminished intervals with the following exercise:
Doubly and Triply Augmented and Diminished Intervals
Intervals can be further contracted or expanded outside of the augmented and diminished qualities. An interval a half step larger than an augmented interval is a doubly augmented interval, while an interval a half step larger than a doubly augmented interval is a triply augmented interval. Likewise, an interval a half step smaller than a diminished interval is a doubly diminished interval, while an interval a half step smaller than a doubly diminished interval is a triply diminished interval.
Compound Intervals
The intervals discussed above, from unison to octave, are simple intervals, which have a size of an octave or smaller. Any interval larger than an octave is a compound interval. In Example 9, the notes A and C first form a minor third (a simple interval). When the C is brought up an octave in the second pair of notes, the interval becomes a minor tenth (a compound interval). Quality remains the same for simple intervals and their corresponding compound intervals.
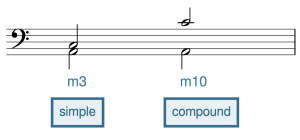
If you want to make a simple interval a compound interval, add 7 to its size. Consequently:
- Unisons (which get the number 1) become octaves (8s)
- 2nds become 9ths
- 3rds become 10ths
- 4ths become 11ths
- 5ths become 12ths
- 6ths become 13ths
These are the most common compound intervals that you will encounter in your music studies. Remember that octaves, 11ths, and 12ths are perfect like their simple counterparts, while 9ths, 10ths, and 13ths are major/minor.
Intervallic Inversion
Intervallic inversion occurs when two notes are “flipped.” In Example 10, for instance, an interval with C on the bottom and E on the top is inverted by moving the C up by an octave. You might be wondering: why is this important? There are two reasons: first, because inverted pairs of notes share many interesting properties (which are sometimes exploited by composers), and second, because inverting a pair of notes can help you to identify or write an interval when you do not want to work from the given bottom note.
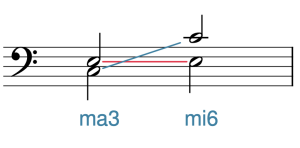
Let’s start with the first point: the interesting properties. First, the size of inverted pairs always adds up to 9:
- Unisons (1s) invert to octaves (8s) (1 + 8 = 9) and octaves invert to unisons.
- Seconds invert to sevenths (2 + 7 = 9) and sevenths invert to seconds.
- Thirds invert to sixths (3 + 6 = 9) and sixths invert to thirds.
- Fourths invert to fifths (4 + 5 = 9) and fifths invert to fourths.
Qualities of inverted pairs of notes are also very consistent:
- Perfect intervals invert to perfect intervals.
- Major intervals invert to minor intervals (and minor intervals to major intervals).
- Augmented intervals invert to diminished intervals (and diminished intervals to augmented intervals).
With that information, you can now calculate the inversions of intervals without even looking at staff paper. For example: a major seventh inverts to a minor second, an augmented sixth inverts to a diminished third, and a perfect fourth inverts to a perfect fifth.

Now for the second point: sometimes you will come across an interval that you do not want to calculate or identify from the bottom note. In the interval E𝄫–A♭ written in Example 11, for instance, identifying the interval using the “Major Scale” method would not work—the bottom note is E𝄫, and there is no key signature for this note (its key signature is “imaginary”). So, if you were given this interval to identify, you might consider inverting the interval. Now the inversion of the interval can be calculated from the non-imaginary key of A♭ major. The key of A♭ major has four flats (B♭, E♭, A♭, and D♭). An E♭ above A♭ would therefore be a perfect fifth; however, this interval has been contracted (made a half step smaller) because the E♭ has been lowered to E𝄫. That means this interval is a d5 (diminished fifth).
Now that we know the inversion of the first interval is a d5, we can calculate the original interval. A diminished fifth inverts to an augmented fourth (because diminished intervals invert to augmented intervals and because five plus four equals nine). Thus, the first interval is an augmented fourth (A4).
Consonance and Dissonance
Intervals are categorized as consonant or dissonant. Consonant intervals are intervals that are considered more stable, as if they do not need to resolve, while dissonant intervals are considered less stable, as if they do need to resolve. These categorizations have varied with milieu. Example 12 shows a table of melodically consonant and dissonant intervals:
| Melodically Consonant | Melodically Dissonant |
|---|---|
| Perfect Intervals | Augmented Intervals |
| ma2, mi2 | Diminished Intervals |
| ma3, mi3 | ma7, mi7 |
| ma6, mi6 |
Example 12. Melodically consonant and dissonant intervals.
Example 13 shows harmonically consonant and dissonant intervals:
| Harmonically Consonant | Harmonically Dissonant |
|---|---|
| ma3, mi3 | ma2, mi2 |
| ma6, mi6 | Augmented Intervals |
| P1, P8, P5 | Diminished Intervals |
| ma7, mi7 | |
| P4 |
Example 13. Harmonically consonant and dissonant intervals.
The implications of consonant and dissonant intervals are discussed further in the Introduction to Species Counterpoint.
Another Method for Intervals: The White-Key Method
Ultimately, intervals need to be committed to memory, both aurally and visually. There are, however, a few tricks to learning how to do this quickly. One such trick is the so-called “white-key method,” which refers to the piano keyboard.
This method requires you to memorize all of the intervals found between the white keys on the piano (or simply all of the intervals in the key of C major). Once you’ve learned these, any interval can be calculated as an alteration of a white-key interval. For example, we can figure out the interval for the notes D and F♯ if we know that the interval D to F is a minor third and this interval has been made one semitone larger: a major third.
Conveniently, there is a lot of repetition of interval size and quality among white-key intervals, summarized in Example 14. Memorize the most frequent type and the exceptions.
- All of the seconds are major except for two: E–F and B–C.
- All of the thirds are minor except for three: C–E, F–A, and G–B, which are major.
- All of the fourths are perfect except for one: F–B, which is an augmented fourth (a tritone).
Example 14. White-key seconds, thirds, and fourths.
Believe it or not, you now know all of the white-key intervals, as long as you understand the concept of intervallic inversion, which was previously explained. For example, if you know that all seconds are major except for E–F and B–C (which are minor), then you know that all sevenths are minor except for F–E and C–B (which are major), as seen in Example 15.

Once you’ve mastered the white-key intervals, you can figure out any other interval by taking into account any accidentals applied to the notes.
Intervallic Enharmonic Equivalence
Example 16 may be useful when thinking about enharmonic equivalence of intervals. In this chart, the columns are different intervallic sizes, while the rows present intervals based on the number of half steps they contain. Each row in this chart is enharmonically equivalent. For example, a major second (ma2) and diminished third (d3) are enharmonically equivalent (both are two half steps). Likewise, an augmented fourth (A4) and diminished fifth (d5) are enharmonically equivalent—both are six half steps in size.
| number of semitones | unis. | 2nd | 3rd | 4th | 5th | 6th | 7th | oct. |
|---|---|---|---|---|---|---|---|---|
| 0 | P1 | d2 | ||||||
| 1 | A1 | mi2 | ||||||
| 2 | ma2 | d3 | ||||||
| 3 | A2 | mi3 | ||||||
| 4 | ma3 | d4 | ||||||
| 5 | A3 | P4 | ||||||
| 6 | A4 | d5 | ||||||
| 7 | P5 | d6 | ||||||
| 8 | A5 | mi6 | ||||||
| 9 | ma6 | d7 | ||||||
| 10 | A6 | mi7 | ||||||
| 11 | ma7 | d8 | ||||||
| 12 | A7 | P8 |
Example 16. Enharmonic equivalence of intervals.
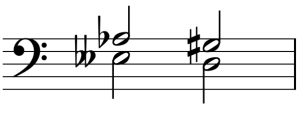
Intervallic enharmonic equivalence is useful when you come across an interval that you do not want to calculate or identify from the bottom note. We have already discussed one method for this situation previously, which was intervallic inversion. You may prefer one method or the other, though both will yield the same result. Example 17 reproduces the interval from Example 11. As you’ll recall, there is no key signature for the bottom note (E𝄫), making identification of this interval difficult. By using enharmonic equivalence, however, we can identify this interval more easily, recognizing that E𝄫 is enharmonically equivalent with D and that A♭ is enharmonically equivalent with G♯. Now we can identify the interval as an A4 (augmented fourth), using the key signature of the enharmonically equivalent bottom note (D).
- Specific Intervals (musictheory.net)
- Interval Introduction (Robert Hutchinson)
- Intervals (Hello Music Theory)
- Diminished and Augmented Intervals (Open Textbooks)
- Diminished and Augmented Intervals (Robert Hutchinson)
- Compound Intervals (Hello Music Theory)
- Interval Inversion (musictheory.net)
- Interval Ear Training (musictheory.net)
- Interval Ear Training (Tone Dear)
- Interval Ear Training (teoria)
- Interval Identification (musictheory.net)
- Keyboard Interval Identification (musictheory.net)
- Interval Identification (.pdf, .pdf, .pdf), in Major Keys (.pdf), in Minor Keys (.pdf)
- Interval Identification and Construction, pp. 18–19 (.pdf)
- Interval Construction (.pdf, .pdf)
- Compound Intervals, pp. 15–17 (.pdf)
Using C clefs:
- Writing and Identifying Intervals Assignment #1 (.pdf, .mcsz)
- Writing and Identifying Intervals Assignment #2 (.pdf, .mcsz)
- Writing and Identifying Intervals Assignment #3 (.pdf, .mcsz)
Treble and bass clef only:
- Writing and Identifying Intervals Assignment #4 (.pdf, .mcsz)
- Writing and Identifying Intervals Assignment #5 (.pdf, .mcsz)
Media Attributions
- Simple Versus Compound © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Inversion © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Imaginary © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- White-key-sevenths © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- Enharmonic Equivalence © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
The distance between two notes.
An interval whose notes are sounded separately (one note after another).
An interval whose notes sound together (simultaneously).
The number of letters (or lines and spaces) that make up the span of an interval. Interval size is written with Arabic numbers (2, 3, 4, etc.).
The number of scale steps between notes of a collection or scale.
A term that indicates the exact number of semitones between two pitches in an interval (compare with interval size, which indicates only the number of letters between two pitches). Common interval qualities are major, minor, perfect, augmented, and diminished.
Intervals that are one half step larger than a perfect or major interval.
Intervals that are one half step smaller than a perfect or minor interval.
An octave or smaller.
An interval that is larger than an octave.
Occurs when two notes are flipped: for instance, C below E is an inversion of E below C.
As an acoustic phenomenon, frequencies vibrating at whole-number ratios with one another; as a cultural phenomenon, perceived stability in a chord or interval.
A perceived quality of auditory roughness in an interval or chord.
A physical and/or social setting.
An ordered collection of half steps (H) and whole steps (W) as follows (ascending): W–W–H–W–W–W–H.
An augmented fourth or diminished fifth. The name reflects that the two notes of a tritone are three (tri-) whole steps (tones) apart.
A relationship between notes, intervals, or chords that sound the same but are spelled differently.

